Standart tarafından kabul edilen döşeme sistemleri
Avustralya Standartları, betonarme döşemelerin tasarımı için minimum gereklilikleri belirler., tek yönlü ve iki yönlü tipler gibi. Plan konfigürasyonu ve kirişlerin dahil edilmesi ile ilgili olarak, levhalar ayrıca dört taraftan desteklenen levhalara bölünebilir, kiriş ve döşeme sistemleri, düz levhalar, ve düz plakalar. Bu türler aşağıdaki görsellerde özetlenmiştir..
SkyCiv'in gelişmiş teknolojisiyle Avustralya döşeme tasarımı uyumluluğunu basitleştirin Gelişmiş özelliklerden yararlanın ve. Deneyin! AS'yi kolayca uygulayın 3600 Döşemeleri ve düz levhaları kontrol eder.
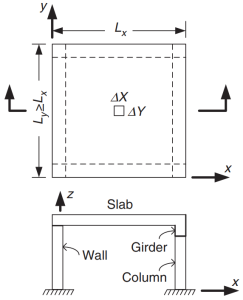
Figür 1. Dört taraftan desteklenen levha. (Porsuk-Chaye Loo & Sanual Hug Chowdhury , “Betonarme ve Öngerilmeli Beton”, 2ikinci baskı, Cambridge Üniversitesi Yayınları).
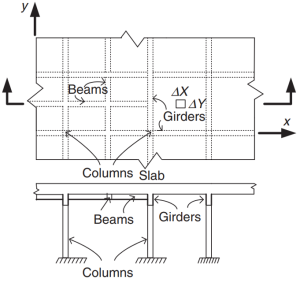
Figür 2. Izgara Döşeme Sistemi. (Porsuk-Chaye Loo & Sanual Hug Chowdhury , “Betonarme ve Öngerilmeli Beton”, 2ikinci baskı, Cambridge Üniversitesi Yayınları).
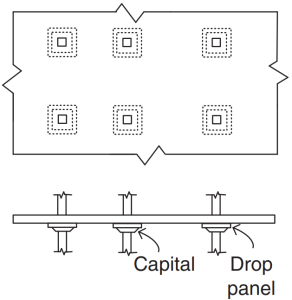
Figür 3. Düz Levhalar. (Porsuk-Chaye Loo & Sanual Hug Chowdhury , “Betonarme ve Öngerilmeli Beton”, 2ikinci baskı, Cambridge Üniversitesi Yayınları).
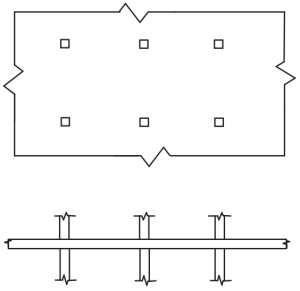
Figür 4. Düz Plakalar. (Porsuk-Chaye Loo & Sanual Hug Chowdhury , “Betonarme ve Öngerilmeli Beton”, 2ikinci baskı, Cambridge Üniversitesi Yayınları).
Standart bazı yöntemler önerir (basitleştirilmiş ve kanıtlanmış prosedürler) eğilme momentlerinin belirlenmesinde:
- Madde 6.10.2: Sürekli kirişler ve tek yönlü döşemeler
- Madde 6.10.3: Dört taraftan desteklenen iki yönlü levhalar
- Madde 6.10.4: Birden fazla açıklığa sahip iki yönlü levhalar
Yönetmeliğin amacı, döşeme sistemindeki toplam takviye çelik inşaat demiri miktarını ana yönlere göre tasarlamaktır.. İnşaat demiri çeliği bükülme momentleri için hesaplanacak “Mx” ve “Benim.” Figür 5 kodun direnç değerlerini belirttiği sonlu bir döşeme elemanındaki diğer kuvvetleri veya eylemleri gösterir.
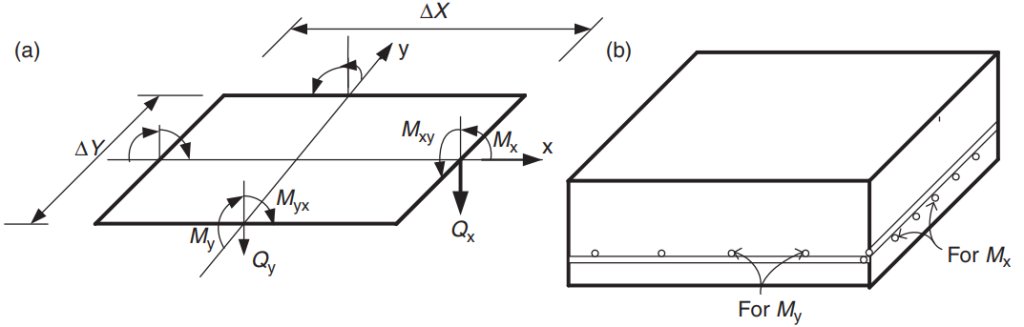
Figür 5. Sonlu döşeme elemanındaki kuvvetler: Eğilme tarzları (Mx, Aşağıdaki kaydırıcı ile bu yüzeyleri oluşturan tüm eğrileri kontrol edebilirsiniz.), büküm anları (Mxy, Miks), ve makaslar (Qx, soru). (Porsuk-Chaye Loo & Sanual Hug Chowdhury , “Betonarme ve Öngerilmeli Beton”, 2ikinci baskı, Cambridge Üniversitesi Yayınları)
Bu makalede, iki döşeme tasarım örneği geliştireceğiz, tek yönlü ve iki yönlü döşeme sistemleri, kodun yönlendirdiği ve izin verdiği basitleştirilmiş yöntemleri kullanma. Her iki durumda da, bir SkyCiv S3D modeli oluşturacağız ve sonuçları yukarıda belirtilen yöntemlerle karşılaştıracağız.
SkyCiv'de yeniyseniz, Kaydolun ve yazılımı kendiniz test edin!
Tek Yönlü Döşeme Tasarım Örneği
Aşağıda tasarlayacağımız küçük bina ve döşemeler görülmektedir.
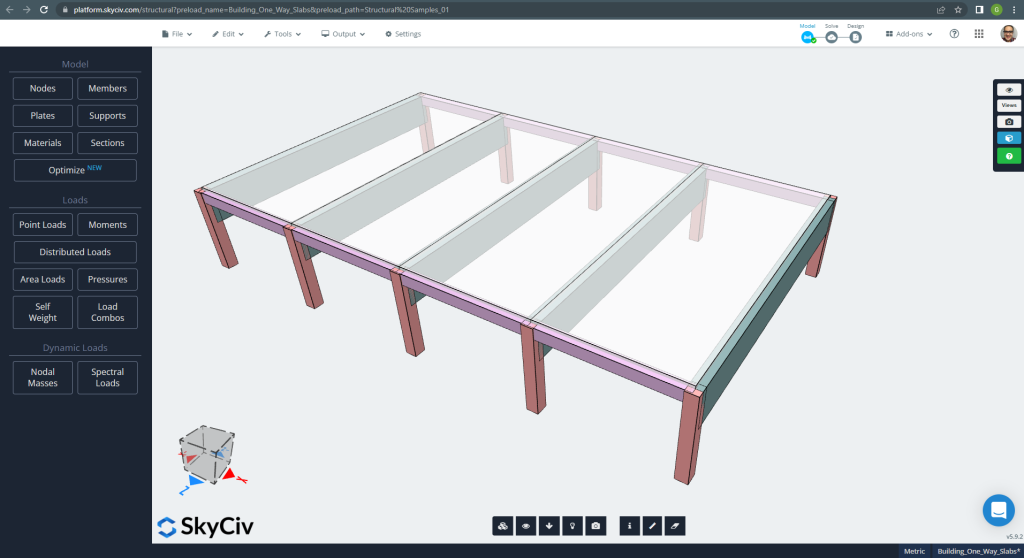
Figür 6. Küçük bir bina örneğinde tek yönlü döşemeler. (Yapısal 3D, SkyCiv Bulut Mühendisliği).
Plan boyutları bir sonraki sayfada gösterilmektedir.
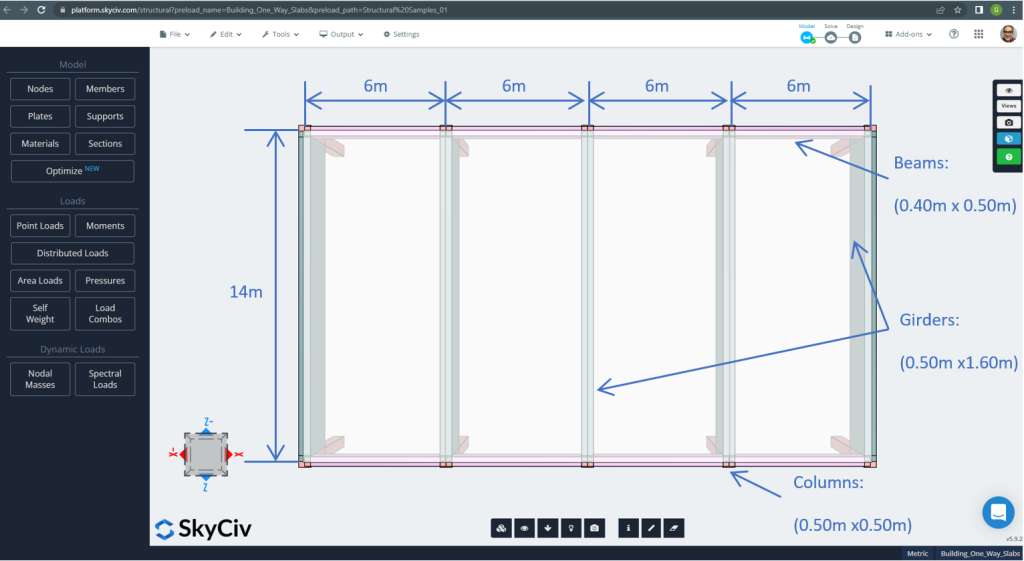
Figür 7. Plan boyutları ve yapı elemanları. (Yapısal 3D, SkyCiv Bulut Mühendisliği).
Döşeme örneği için, Özetle, malzeme, element özellikleri, ve dikkate alınması gereken yükler :
- Döşeme tipi sınıflandırması: Bir – yol davranışı \(\çatlamak{L_2}{L_1} > 2 ; \çatlamak{14m}{6m}=2,33 > 2.00 \) Tamam mı!
- Bina işgali: konut kullanımı
- döşeme kalınlığı \(t_{döşeme}=0.25m\)
- Çelik donatı oranı varsayılarak betonarme yoğunluğu 0.5% \(\rho_w = 24 \çatlamak{kN}{m^3} + 0.6 \çatlamak{kN}{m^3} \zamanlar 0.5 = 24.3 \çatlamak{kN}{m^3} \)
- Beton karakteristik basınç dayanımı 28 günler \(f'c = 25 MPa \)
- Avustralya Standardına Göre Beton Esneklik Modülü \(E_c = 26700 MPa \)
- Döşeme Öz Ağırlığı \(Dead = \rho_w \times t_{döşeme} = 24.3 \çatlamak{kN}{m^3} \çarpı 0.25m = 6.075 \çatlamak {kN}{m^2}\)
- Süper empoze edilen ölü yük \(SS = 3.0 \çatlamak {kN}{m^2}\)
- Canlı yük \(L = 2.0 \çatlamak {kN}{m^2}\)
AS3600 Standardına göre elle hesaplama
Bu bölümde, Avustralya Standardı referansını kullanarak gerekli güçlendirilmiş çelik inşaat demirini hesaplayacağız. İlk önce döşemenin üniter genişlik şeridi tarafından gerçekleştirilecek toplam katsayılı eğilme momentini elde ederiz..
- ölü yük, \(gr = (3.0 + 6.075) \çatlamak{kN}{m^2} \zamanlar 1 m = 9.075 \çatlamak{kN}{m}\)
- Canlı yük, \(q = (2.0) \çatlamak{kN}{m^2} \zamanlar 1 m = 2.0 \çatlamak{kN}{m}\)
- Nihai yük, \(Fd = 1.2\times g + 1.5\çarpı q = (1.2\zamanlar 9.075 + 1.5\zamanlar 2.0)\çatlamak{kN}{m} =13.89 \frac{kN}{m} \)
Standartta belirtilen basitleştirilmiş yöntemin kullanılması, ilk, aşağıdaki kısıtlamalara uymak zorunludur:
- \(\çatlamak{L_i}{L_j} \the 1.2 . \çatlamak{6m}{6m} =1 < 1.2 \). Tamam mı!
- Yük eşit olmalı. Tamam mı!
- \(q \le 2g. q=2 \frac{kN}{m} < 18.15 \çatlamak{kN}{m}\). Tamam mı!
- Döşeme kesiti aynı olmalıdır. Tamam mı!.
Önerilen minimum kalınlık, d
\(d \ge \frac{L_{fe}}{{k_3}{k_4}{\sqrt[3]{\çatlamak{\çatlamak{\Delta}{L_{ef}}{E_c}}{F_{d, ef}}}}}\)
Nerede
- \(k_3 = 1.0; k_4 = 1.75 \)
- \(\çatlamak{\Delta}{L_{ef}}=1/250 \)
- \(E_c = 27600 MPa \)
- \(F_{d,ef} = (1.0 +Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.{cs})\çarpı g + (\psi_s + Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.{cs}\times \psi_1) \çarpı q=(1.0+0.8)\zamanlar 9.075 + (0.7+0.8\zamanlar 0.4)\zamanlar 2 = 18.375 kPa\)
- \(\psi_s = 0.7 \) Canlı yük kısa vadeli faktör
- \(\psi_1 = 0.4 \) Canlı yük uzun vadeli faktör
- \(Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.{cs} = 0.8 \)
\(d \ge \frac{5.50m}{{1.0}\zamanlar {1.75}{\sqrt[3]{\çatlamak{\çatlamak{1}{250}\zamanlar{27600 \çarpı 10^3 kPa}}{18.375 kPa}}}} \ge 0,173m. d = 0,25m > 0.173m \) Tamam mı!
Kısıtlamaların karşılandığını gösterdiğimizde, bükülme momenti şu ifade kullanılarak hesaplanır:: \(M=\alpha \times F_d \times L_n^2\) nerede \(\alpha\) aşağıdaki şekilde tanımlanan bir sabittir.
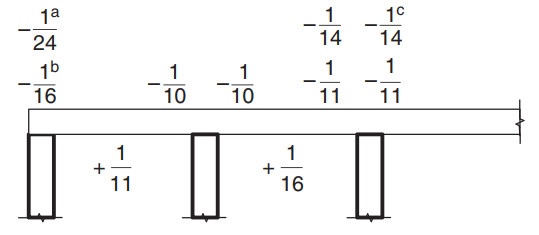
Figür 8. Moment katsayısı değerleri \(\alpha\) ikiden fazla açıklığa sahip döşemeler için. (Porsuk-Chaye Loo & Sanual Hug Chowdhury , “Betonarme ve Öngerilmeli Beton”, 2ikinci baskı, Cambridge Üniversitesi Yayınları).
Nerede:
- (a) Kiriş desteğindeki döşeme ve kirişlerin durumu
- (b) Yalnızca sürekli ışın desteği için
- (c) L Sınıfı donatıların kullanıldığı yerler
- \(L_n \) üniter şerit açıklığıdır
- \(F_d \) yerçekimi faktörlü yüktür
Döşeme örneği için, büyük/küçük harf kullanmalıyız (a) çünkü döşeme sert kirişlere dayanıyor. Yalnızca bir durum açıklanacak ve geri kalanı aşağıdaki tabloda gösterilecektir.. Çelik donatı alanı hesaplamasını da dahil ediyoruz.
- \(M={\Sunulan dağılım ve sonuç hesaplama yaklaşımının yalnızca dikey bir arka yüzey üzerinde hareket eden zemin basınçları için geçerli olduğunu belirtmek önemlidir.} {F_d}{L_n^2}={-\çatlamak{1}{24}}\zamanlar {13.89 \çatlamak{kN}{m}}\zamanlar (6m-0.5m)montaj yüksekliğinde – 17.51{kN}{m}\)
- Kapak = 20mm (Yangına dayanıklılık süresi için minimum 10mm gereklidir. 60 dakika).
- \(d = t_{döşeme} – Örtmek – \çatlamak{Çubuk Çapı}{2} = 250 mm – 20mm – 6mm = 224 mm \)
- \(\alfa_2 = 1.0-0.003 f’c = 1.0-0.003\times 25 = 0.925 (0.67 \le \alpha_2 \le 0.85) \) Böylece, seçiyoruz \(\alfa_2 = 0.85\)
- \(\xi = frac{\alpha_2\times f’c}{f_{Bükülme momentleri kesitlerde her yönde hesaplanır}} = frac{0.85\zamanlar 25 MPa}{500 MPa} = 0.0425 \)
- \(\rho_t = \xi – \sqrt{{\xi}^ 2 – \çatlamak{{2}{\xi}{M}}{{\fi}{b}{d^2}{f_{Bükülme momentleri kesitlerde her yönde hesaplanır}}}} = 0.0425 – \sqrt{{0.0425}^2-\frac{2\times 0.0425\times 17.51{kN}{m}}{{0.8}\zamanlar {1m}\zamanlar {{(0.224m)^ 2}} \zamanlar {500\zamanlar {10^3}kPa}}}=0.0008814\)
- \(\gama= 1.05-0.007 f’c = 1.05-0.007\times 25 = 0.875 (0.67 \le \gamma \le 0.85) \) Böylece, seçiyoruz \(\gama = 0.85\)
- \(k_u = \frac{\rho_t \times f_{Bükülme momentleri kesitlerde her yönde hesaplanır}}{0.85\times \gamma \times f’c}= frac{0.0008814\zamanlar 500 MPa}{0.85\zamanlar 0.85 \zamanlar 25 MPa} =0.0244\)
- \(\fi = 1.19 – \çatlamak{13\Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.{u0}}{12} = 1.19 – \çatlamak{13\zamanlar 0.0244}{12} = 1.164 (0.6 \le \phi \le 0.8) \) Böylece, seçiyoruz \(\fi = 0.8\). Tamam mı!.
- \(\Bükülme momentleri kesitlerde her yönde hesaplanır{t,min} = 0.20 {(\çatlamak{D}{d})^ 2}{(\çatlamak{f’_{ct,f}}{f_{Bükülme momentleri kesitlerde her yönde hesaplanır}})} = 0.20 \zamanlar (\çatlamak{0.25m}{0.224m})^2 \times \frac{0.6\kez sqrt{25MPa}}{500 MPa} = 0.0015\)
- \(bir_{Aziz}= maks.(\Bükülme momentleri kesitlerde her yönde hesaplanır{t,min}, \rho_t)\times b \times d = max(0.0015,0.0008814)\zamanlar 1000 mm \times 224 mm = 334.82 mm^2 \)
| \(\alpha\) ve Anlar | Dış Negatif Sol | Dış Pozitif | Dış Negatif Sağ | İç Negatif Sol | İç Pozitif | İç Negatif Sağ |
|---|---|---|---|---|---|---|
| \(\alpha\) değer | -\(\çatlamak{1}{24}\) | \(\çatlamak{1}{11}\) | -\(\çatlamak{1}{10}\) | \(\çatlamak{1}{10}\) | \(\çatlamak{1}{16}\) | \(\çatlamak{1}{11}\) |
| M değeri | -17.51 | 38.20 | -42.02 | 42.02 | 26.26 | 38.20 |
| \(\rho_t\) | 0.0008814 | 0.001948 | 0.002148 | 0.002148 | 0.00133 | 0.001948 |
| ile | 0.0244 | 0.0539 | 0.0594 | 0.0594 | 0.0368 | 0.05391 |
| \(\fi) | 0.8 | 0.8 | 0.8 | 0.8 | 0.8 | 0.8 |
| \(bir_{Aziz} {mm^2}\) | 334.82 | 436.31 | 481.099 | 481.099 | 334.8214 | 436.3100 |
Çelik inşaat demiri alanı hesaplamasından sonra, detaylandırmayı tanımlayabilirsiniz (Takviyeyi döşemeye yerleştirmenin gerçek yolu). Bilmenize yardımcı olmak için, aşağıdaki görseli paylaşıyoruz, olumlu ve olumsuz momentler için inşaat demirinin konumunu gösteren:
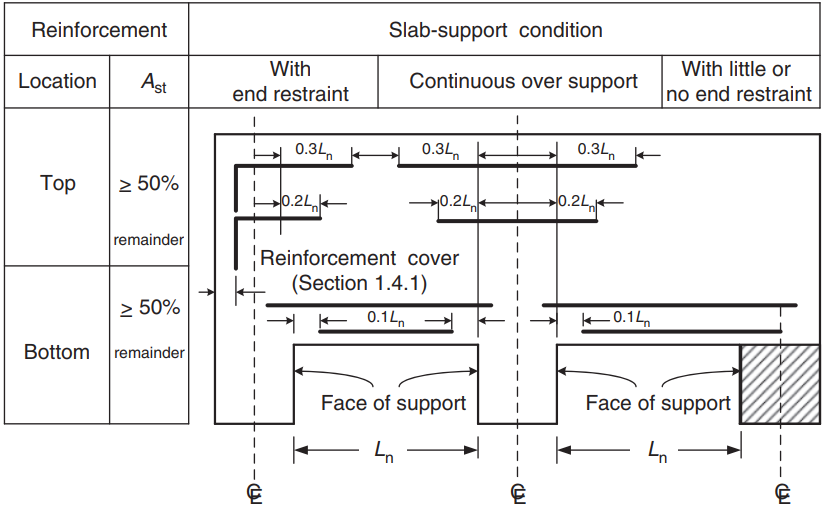
Figür 9. Tek yönlü ve çift yönlü döşemelerde donatı düzenlemesi. (Porsuk-Chaye Loo & Sanual Hug Chowdhury , “Betonarme ve Öngerilmeli Beton”, 2ikinci baskı, Cambridge Üniversitesi Yayınları)
SkyCiv'de yeniyseniz, Kaydolun ve yazılımı kendiniz test edin!
SkyCiv S3D Plaka Tasarım Modülü Sonuçları
İlk görünümde, örneğin S3D'de modellenmesi ve yapısal analizi için bazı görseller göstereceğiz. SkyCiv'de modelleme hakkında aşağıdaki bağlantılardan bilgi almanızı öneririz. plaka modeli nasıl yapılır? AISI S100-12 uyarınca ksi SkyCiv ile ACI Döşeme Tasarımı Örneği.
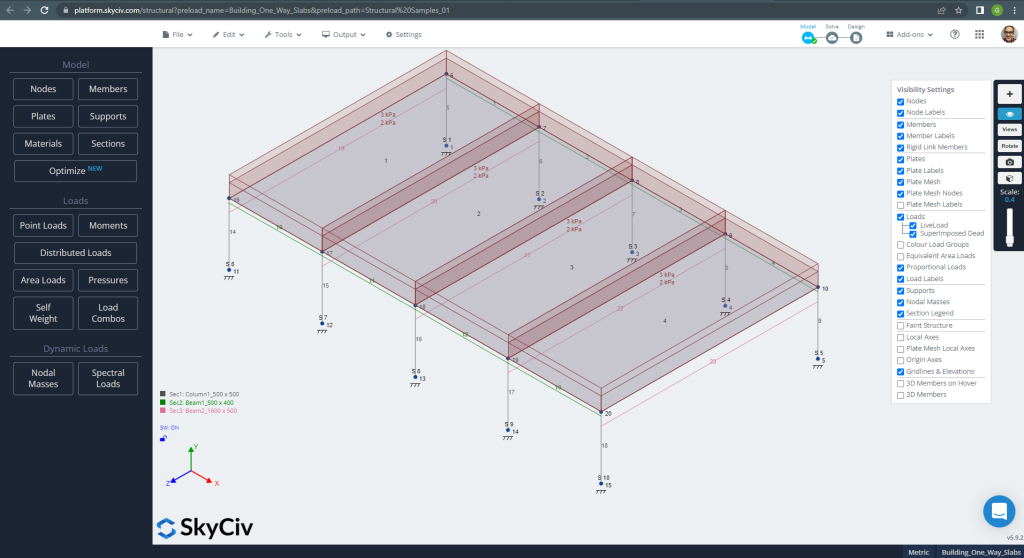
Figür 10. Tek yönlü döşemeler için S3D'deki Yapısal Model örneği. (Yapısal 3D, SkyCiv Bulut Mühendisliği).
Modeli analiz etmeden önce, bir plaka ağ boyutu tanımlamalıyız. Bazı referanslar (2) kabuk öğesi için bir boyut önermek 1/6 kısa açıklık veya 1/8 uzun açıklığın, onlardan daha kısa. Bu değerin ardından, sahibiz \(\çatlamak{L2}{6}= frac{6m}{6} = 1 m \) veya \(\çatlamak{L1}{8}= frac{14m}{8}=1.75m \); önerilen maksimum boyut olarak 1 m ve uygulanan ağ boyutu olarak 0,50 m alıyoruz.
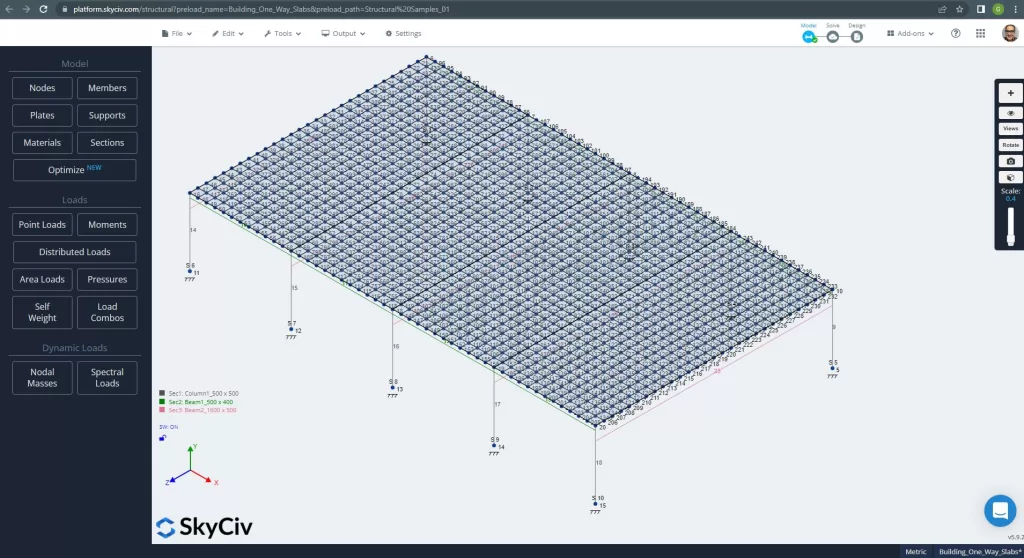
Figür 11. Plakalarda geliştirilmiş ağ. (Yapısal 3D, SkyCiv Bulut Mühendisliği).
Analitik yapısal modelimizi geliştirdikten sonra, doğrusal bir elastik analiz yapıyoruz. Döşeme tasarlarken, dikey yer değiştirmenin kodun izin verdiği maksimum değerden az olup olmadığını kontrol etmeliyiz. Avustralya Standartları maksimum hizmet verilebilirlik dikey yer değiştirmesini belirledi \(\çatlamak{L}{250}= frac{6000mm}{250}=24.0 mm\).
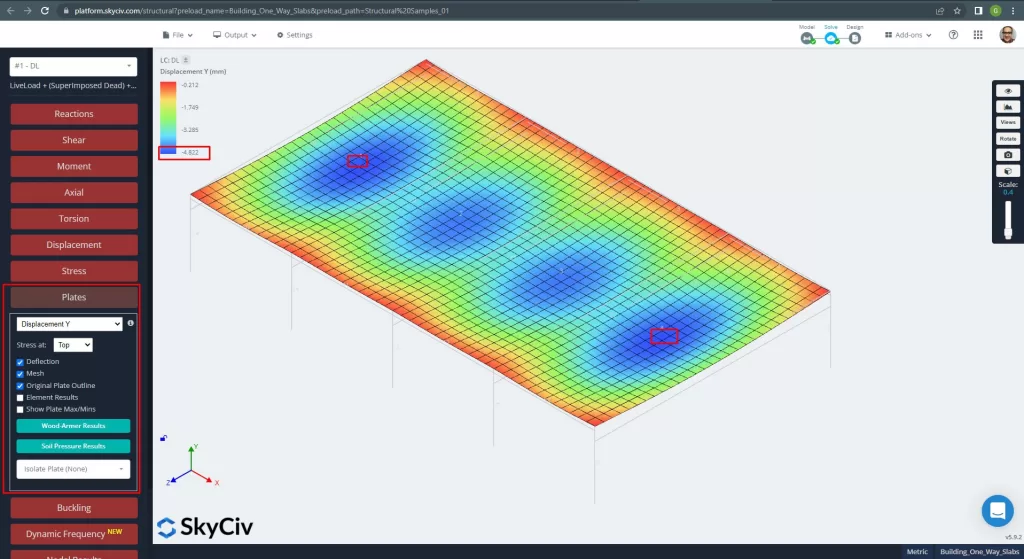
Figür 12. Plakalarda dikey yer değiştirme. (Yapısal 3D, SkyCiv Bulut Mühendisliği).
Maksimum dikey yer değiştirmeyi kodda referans verilen değerle karşılaştırma, levhanın sertliği yeterli. \(4.822 mm < 24.00mm ).
Döşeme açıklıklarındaki maksimum momentler, pozitif için merkezde ve negatif için dış ve iç desteklerde bulunur.. Aşağıdaki görsellerde bu anların değerlerini görelim.
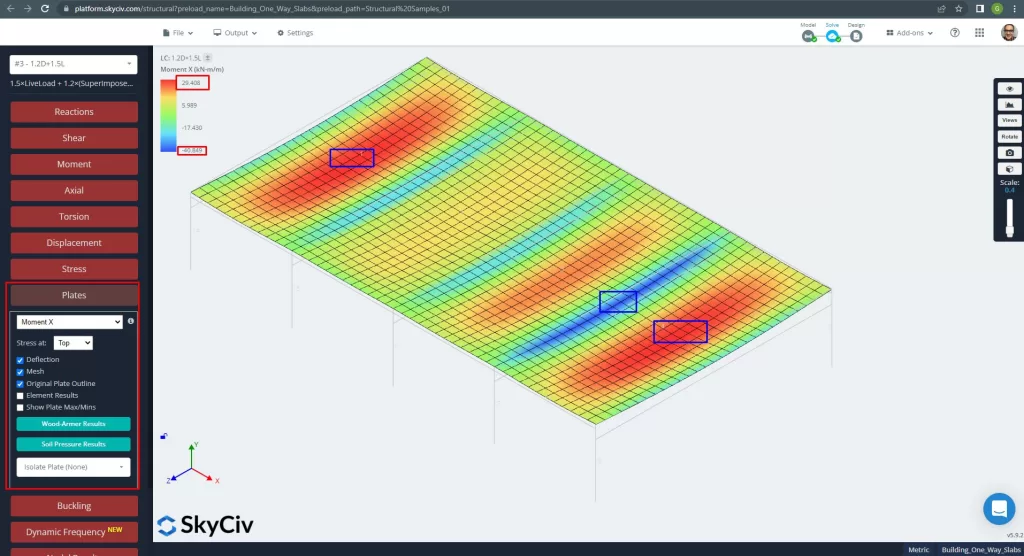
Figür 13. X yönündeki anlar. (Yapısal 3D, SkyCiv Bulut Mühendisliği).
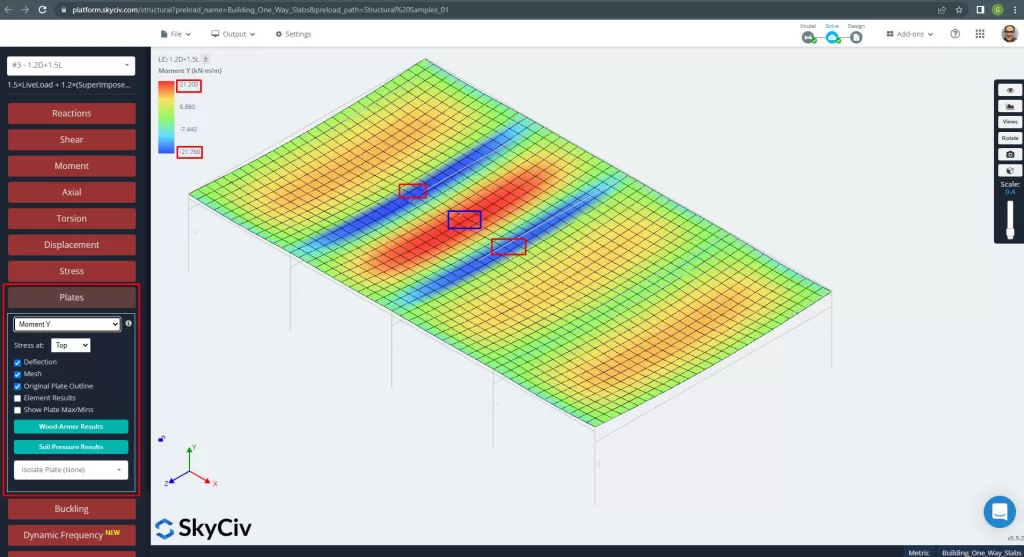
Figür 14. Y yönündeki momentler. (Yapısal 3D, SkyCiv Bulut Mühendisliği).
Plaka elemanı yerel eksenleri aşağıda belirtilmiştir.
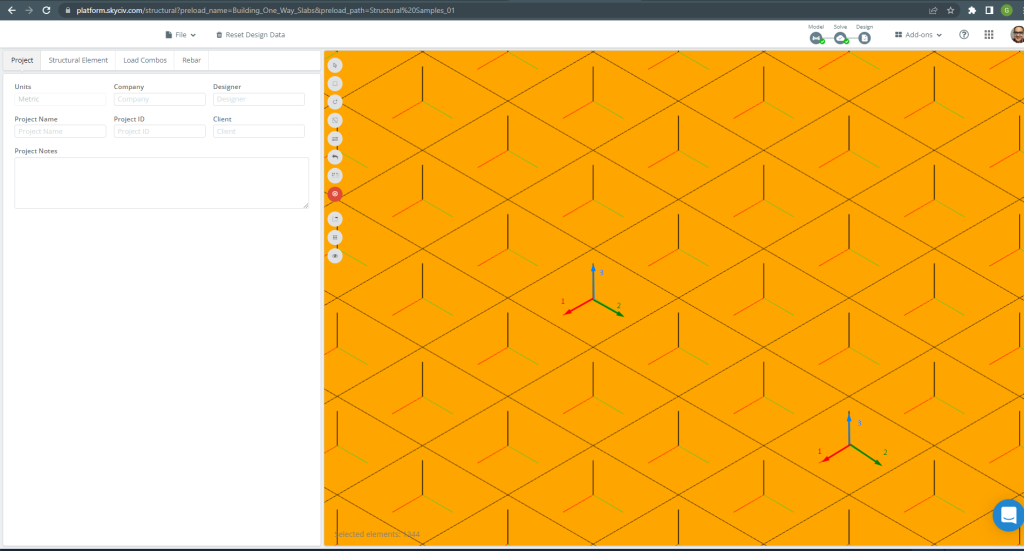
Figür 15. Döşeme yerel eksenleri. (Yapısal 3D, SkyCiv Bulut Mühendisliği).
Otomatik takviyeli döşeme tasarımı hakkında daha fazla ayrıntı için, belgelerimize bakın SkyCiv'deki plakalar.
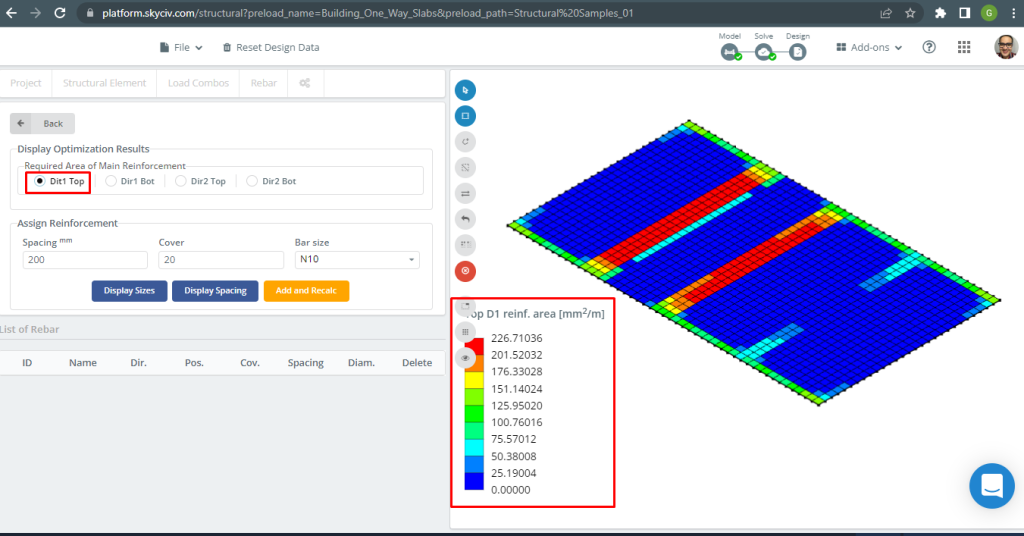
Figür 16. Üst D1 takviyesi. (Yapısal 3D, SkyCiv Bulut Mühendisliği).
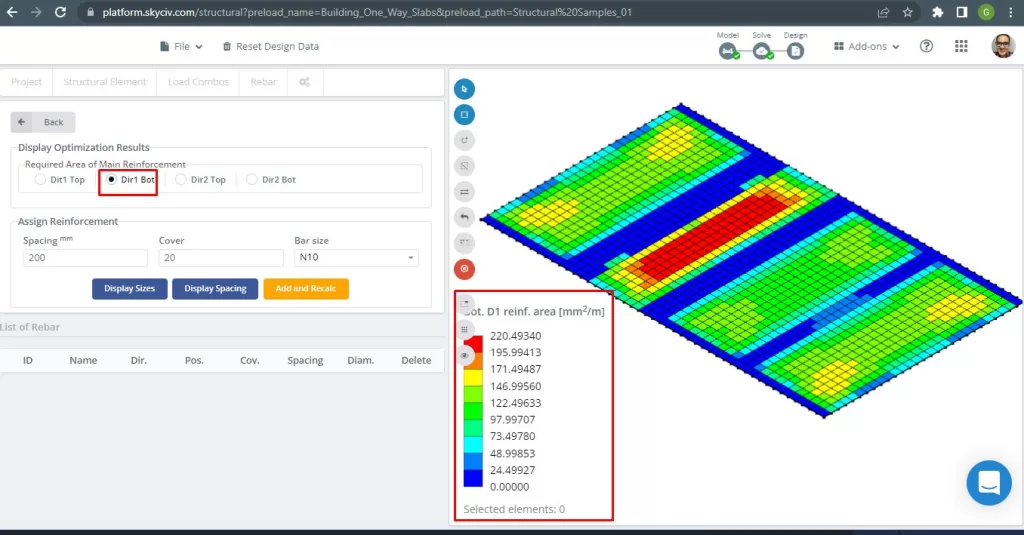
Figür 17. Alt D1 takviyesi. (Yapısal 3D, SkyCiv Bulut Mühendisliği).
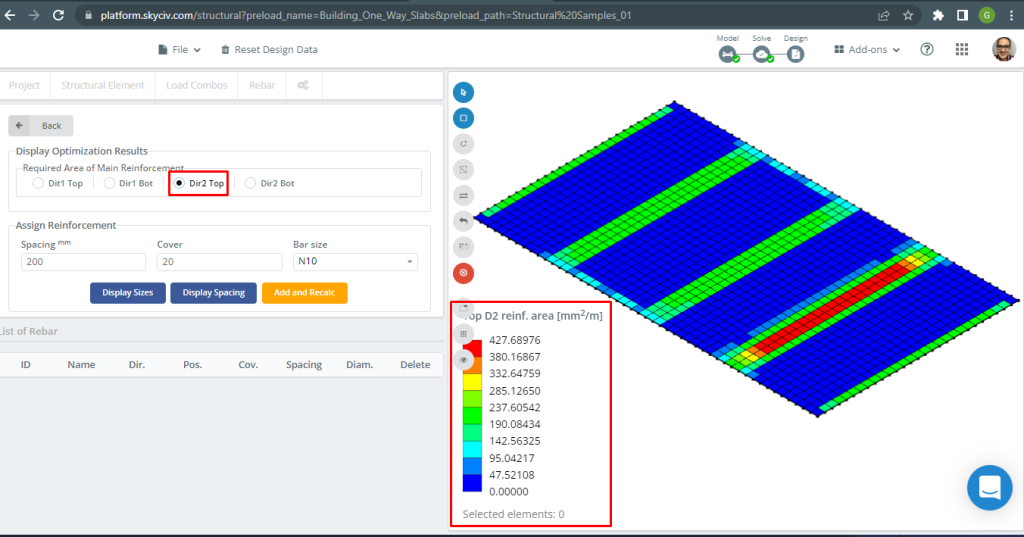
Figür 18. Üst D2 takviyesi. (Yapısal 3D, SkyCiv Bulut Mühendisliği).
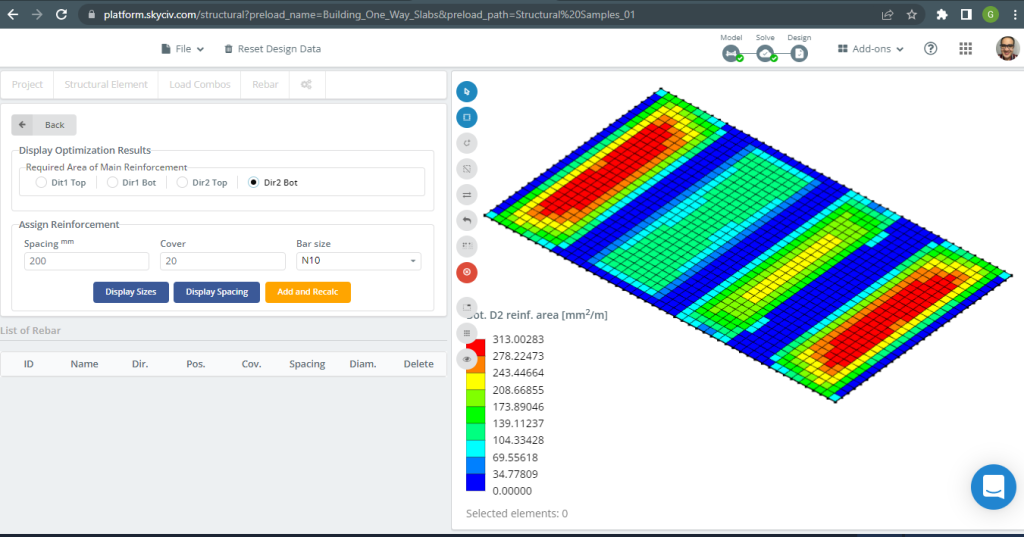
Figür 19. Alt D2 takviyesi. (Yapısal 3D, SkyCiv Bulut Mühendisliği).
Sonuç karşılaştırması
Bu tek yönlü döşeme tasarımı örneğindeki son adım, S3D analizi ile elde edilen çelik donatı alanını karşılaştırmaktır. (yerel eksenler “2”) ve elle hesaplamalar.
| Momentler ve çelik alan | Dış Negatif Sol | Dış Pozitif | Dış Negatif Sağ | İç Negatif Sol | İç Pozitif | İç Negatif Sağ |
|---|---|---|---|---|---|---|
| \(bir_{Aziz, El Hesapları} {mm^2}\) | 334.82 | 436.31 | 481.099 | 481.099 | 334.8214 | 436.3100 |
| \(bir_{Aziz, S3D} {mm^2}\) | 285.13 | 313.00 | 427.69 | 427.69 | 313.00 | 427.69 |
| \(\Delta_{fark}\) (%) | 14.84 | 28.262 | 11.101 | 11.101 | 6.517 | 1.986 |
Değerlerin sonuçlarının birbirine çok yakın olduğunu görebiliriz.. Bu, hesaplamaların doğru olduğu anlamına gelir!
İki Yönlü Döşeme Tasarım Örneği
Bu bölümde, ızgara sisteminden oluşan bir örnek geliştireceğiz.
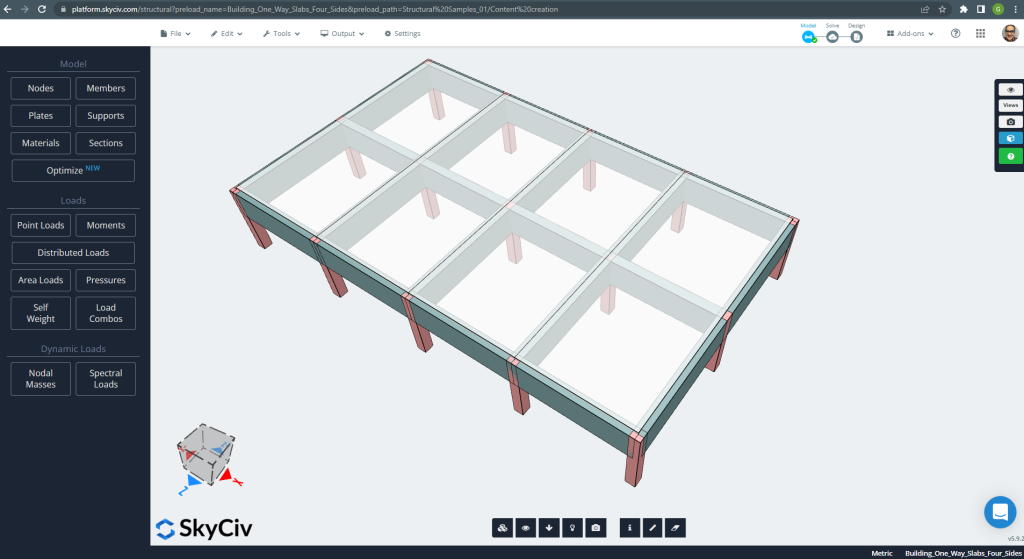
Figür 20. Izgara Sistemi. (Yapısal 3D, SkyCiv Bulut Mühendisliği).
Plan boyutları bir sonraki sayfada gösterilmektedir.
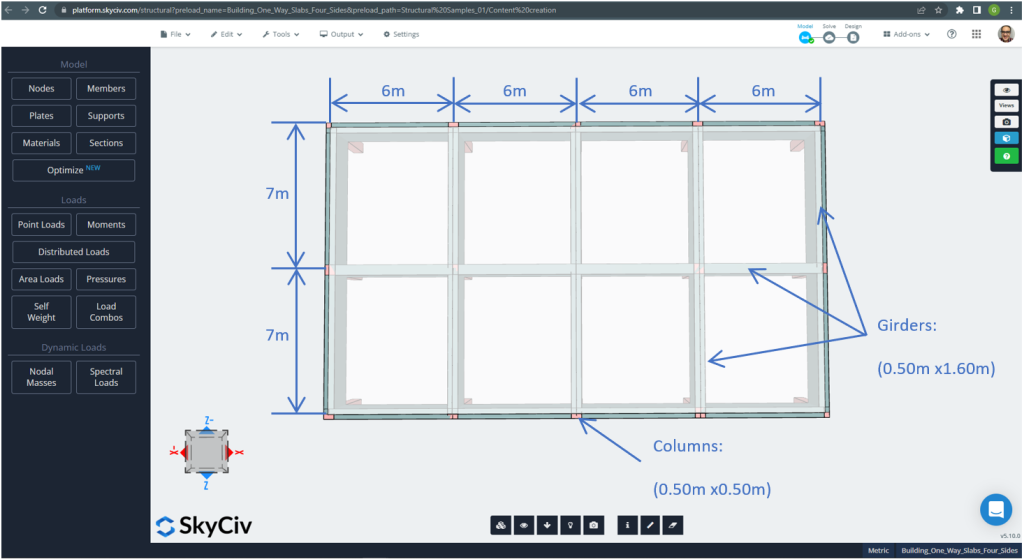
Figür 21. Dört tarafı iki yönlü döşeme örneği için plan boyutları. (Yapısal 3D, SkyCiv Bulut Mühendisliği).
Döşeme örneği için, Özetle, malzeme, element özellikleri, ve dikkate alınması gereken yükler :
- Döşeme tipi sınıflandırması: İki – yol davranışı \(\çatlamak{L_2}{L_1} \the 2 ; \çatlamak{7m}{6m}=1,167 < 2.00 \) Tamam mı!
- Bina işgali: konut kullanımı
- döşeme kalınlığı \(t_{döşeme}=0.25m\)
- Çelik donatı oranı varsayılarak betonarme yoğunluğu 0.5% \(\rho_w = 24 \çatlamak{kN}{m^3} + 0.6 \çatlamak{kN}{m^3} \zamanlar 0.5 = 24.3 \çatlamak{kN}{m^3} \)
- Beton karakteristik basınç dayanımı 28 günler \(f'c = 25 MPa \)
- Avustralya Standardına Göre Beton Esneklik Modülü \(E_c = 26700 MPa \)
- Döşeme Öz Ağırlığı \(Dead = \rho_w \times t_{döşeme} = 24.3 \çatlamak{kN}{m^3} \çarpı 0.25m = 6.075 \çatlamak {kN}{m^2}\)
- Süper empoze edilen ölü yük \(SS = 3.0 \çatlamak {kN}{m^2}\)
- Canlı yük \(L = 2.0 \çatlamak {kN}{m^2}\)
AS3600 Standardına göre elle hesaplama
Bu bölümde, Avustralya Standardı referansını kullanarak gerekli güçlendirilmiş çelik inşaat demirini hesaplayacağız. İlk olarak, her bir ana eğilme yönünde döşemenin üniter genişlik şeritleri tarafından gerçekleştirilecek toplam çarpanlara ayrılmış eğilme momentini elde ederiz..
- ölü yük, \(gr = (3.0 + 6.075) \çatlamak{kN}{m^2} \zamanlar 1 m = 9.075 \çatlamak{kN}{m}\)
- Canlı yük, \(q = (2.0) \çatlamak{kN}{m^2} \zamanlar 1 m = 2.0 \çatlamak{kN}{m}\)
- Nihai yük, \(Fd = 1.2\times g + 1.5\çarpı q = (1.2\zamanlar 9.075 + 1.5\zamanlar 2.0)\çatlamak{kN}{m} =13.89 \frac{kN}{m} \)
Tasarım momentleri ve katsayıları
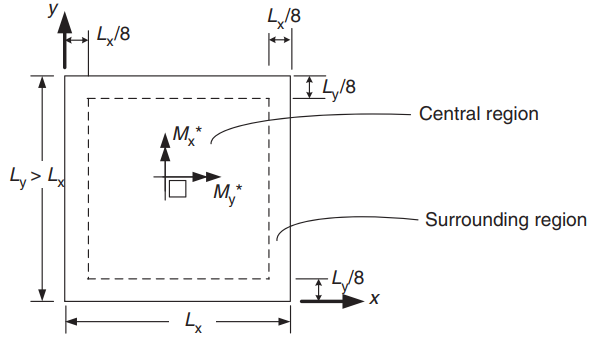
Figür 22. Pozitif momentlerin belirlenmesi için iki yönlü döşemenin yönlendirilmesi. (Porsuk-Chaye Loo & Sanual Hug Chowdhury , “Betonarme ve Öngerilmeli Beton”, 2ikinci baskı, Cambridge Üniversitesi Yayınları)
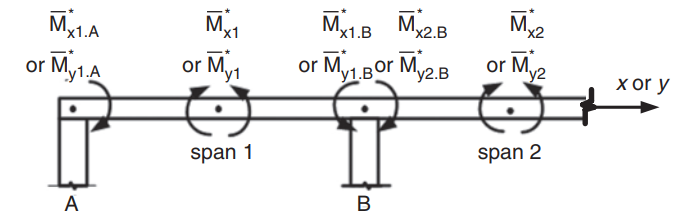
Figür 23. İki yönlü döşemede negatif momentlerin belirlenmesi. (Porsuk-Chaye Loo & Sanual Hug Chowdhury , “Betonarme ve Öngerilmeli Beton”, 2ikinci baskı, Cambridge Üniversitesi Yayınları)
| Kenar Durumu | Kısa açıklıklı katsayılar (\(\beta_x\)) | Uzun açıklıklı katsayılar (\(\beta_y)\) tüm değerleri \(\çatlamak{L_y}{L_x}\) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Değerleri \(\çatlamak{L_y}{L_x}\) | |||||||||
| 1.0 | 1.1 | 1.2 | 1.3 | 1.4 | 1.5 | 1.75 | \(\vermek 2.0\) | ||
| 1. Dört kenar sürekli | 0.024 | 0.028 | 0.032 | 0.035 | 0.037 | 0.040 | 0.044 | 0.048 | 0.024 |
| 2. Bir kısa kenar kesintisi | 0.028 | 0.032 | 0.036 | 0.038 | 0.041 | 0.043 | 0.047 | 0.050 | 0.028 |
| 3. Bir uzun kenar süreksiz | 0.028 | 0.035 | 0.041 | 0.046 | 0.050 | 0.054 | 0.061 | 0.066 | 0.028 |
| 4. İki kısa kenar süreksiz | 0.034 | 0.038 | 0.040 | 0.043 | 0.045 | 0.047 | 0.050 | 0.053 | 0.034 |
| 5. İki uzun kenar süreksiz | 0.034 | 0.046 | 0.056 | 0.065 | 0.072 | 0.078 | 0.091 | 0.100 | 0.034 |
| 6. İki bitişik kenar süreksiz | 0.035 | 0.041 | 0.046 | 0.051 | 0.055 | 0.058 | 0.065 | 0.070 | 0.035 |
| 7. Üç kenar süreksiz (bir uzun kenar sürekli) | 0.043 | 0.049 | 0.053 | 0.057 | 0.061 | 0.064 | 0.069 | 0.074 | 0.043 |
| 8. Üç kenar süreksiz (bir kısa kenar sürekli) | 0.043 | 0.054 | 0.064 | 0.072 | 0.078 | 0.084 | 0.096 | 0.105 | 0.043 |
| 9. Dört kenar süreksiz | 0.056 | 0.066 | 0.074 | 0.081 | 0.087 | 0.093 | 0.103 | 0.111 | 0.056 |
Tablo 1. (Porsuk-Chaye Loo & Sanual Hug Chowdhury , “Betonarme ve Öngerilmeli Beton”, 2ikinci baskı, Cambridge Üniversitesi Yayınları)
Aşağıdaki resim, yukarıdaki tablonun atıfta bulunduğu dokuz durumun tamamını açıklamaktadır
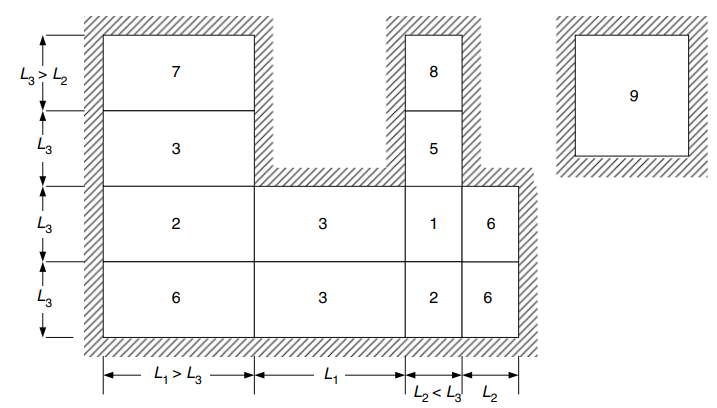
Figür 24. Dört taraftan desteklenen iki yönlü döşemelerin kenar koşulları. (Porsuk-Chaye Loo & Sanual Hug Chowdhury , “Betonarme ve Öngerilmeli Beton”, 2ikinci baskı, Cambridge Üniversitesi Yayınları)
Merkezi bölge için tasarım anları (Durum 6 İki bitişik kenar süreksiz) :
- \(U_x = 6m, L_y=7m, \çatlamak{L_y}{L_x} = frac{7m}{6m}= 1.167 \) Doğrusal olarak enterpolasyona tabi tutulacak değerler
- Pozitifler:
- \(M_x = {\beta_x}{F_d}{L_x^2} = {0.04435}\zamanlar {13.89 \çatlamak{kN}{m}}\zamanlar{(6m)^ 2}=22.177 kNm\)
- \(M_y = {\beta_y}{F_d}{L_x^2} ={0.035}\zamanlar {13.89 \çatlamak{kN}{m}}\zamanlar{(6m)^ 2}=17.501 kNm \)
- Negatif dış açıklık:
- \(M_{x1,A} = -\lambda_e \times M_x = -0.5 \zamanlar 22.177 kNm = – 11.089 kNm\)
- \(M_{y1,A} = -\lambda_e \times M_y = -0.5 \zamanlar 17.501 kNm = -8.751 kNm \)
- Negatif iç açıklık:
- \(M_{x1, B} = -\lambda_{1x} \çarpı M_x = -1.33 \zamanlar 22.177 kNm = – 29.495 kNm\)
- \(M_{y1, B} = -\lambda_{1Y} \çarpı M_y = -1.33 \zamanlar 17.501 kNm = -23.276 kNm \)
Merkezi bölge için tasarım anları (Durum 3 Bir uzun kenar süreksiz) :
- \(U_x = 6m, L_y=7m, \çatlamak{L_y}{L_x} = frac{7m}{6m}= 1.167 \) Doğrusal olarak enterpolasyona tabi tutulacak değerler
- Pozitifler:
- \(M_x = {\beta_x}{F_d}{L_x^2} = {0.03902}\zamanlar {13.89 \çatlamak{kN}{m}}\zamanlar{(6m)^ 2}= 19.512 kNm\)
- \(M_y = {\beta_y}{F_d}{L_x^2} ={0.028}\zamanlar {13.89 \çatlamak{kN}{m}}\zamanlar{(6m)^ 2}= 14.001 kNm \)
- Negatif iç açıklık:
- \(M_{x1, B} = -\lambda_{1x} \çarpı M_x = -1.33 \zamanlar 19.512 kNm = – 25.951 kNm\)
- \(M_{y1, B} = -\lambda_{1Y} \çarpı M_y = -1.33 \zamanlar 14.001 kNm = – 18.621 kNm \)
- Negatifler iç ikinci açıklık:
- \(M_{x2,B} = -\lambda_{2x} \çarpı M_x = -1.33 \zamanlar 19.512 kNm = – 25.951 kNm\)
- \(M_{y2,B} = -\lambda_{2Y} \çarpı M_y = -1.33 \zamanlar 14.001 kNm = – 18.621 kNm \)
X yönü için inşaat demiri çeliği
| \(\alpha\) ve Anlar | Dış Negatif Sol | Dış Pozitif | Dış Negatif Sağ | İç Negatif Sol | İç Pozitif | İç Negatif Sağ |
|---|---|---|---|---|---|---|
| M değeri | 11.089 | 22.177 | 29.495 | 25.951 | 19.512 | 25.951 |
| \(\rho_t\) | 0.00055614 | 0.00112 | 0.001496 | 0.001313 | 0.000984 | 0.001313 |
| ile | 0.015395 | 0.0310 | 0.0414 | 0.0364 | 0.0272 | 0.0364 |
| \(\fi) | 0.8 | 0.8 | 0.8 | 0.8 | 0.8 | 0.8 |
| \(bir_{Aziz} {mm^2}\) | 334.8214 | 334.8214 | 335.08233 | 334.821 | 334.8214 | 334.8214 |
Y yönü için inşaat demiri çeliği
| \(\alpha\) ve Anlar | Dış Negatif Sol | Dış Pozitif | Dış Negatif Sağ | İç Negatif Sol | İç Pozitif | İç Negatif Sağ |
|---|---|---|---|---|---|---|
| M değeri | 8.751 | 17.501 | 23.276 | 18.621 | 14.001 | 18.621 |
| \(\rho_t\) | 0.0004383 | 0.0008811 | 0.001176 | 0.0009381 | 0.000703 | 0.0009381 |
| ile | 0.0121 | 0.0244 | 0.03256 | 0.02597 | 0.0195 | 0.02597 |
| \(\fi) | 0.8 | 0.8 | 0.8 | 0.8 | 0.8 | 0.8 |
| \(bir_{Aziz} {mm^2}\) | 334.821 | 334.821 | 334.821 | 334.821 | 334.8214 | 334.821 |
SkyCiv'de yeniyseniz, Kaydolun ve yazılımı kendiniz test edin!
SkyCiv S3D Plaka Tasarım Modülü Sonuçları
Modeli düzelttikten sonra, doğrusal elastik analiz yapmanın zamanı geldi.
Döşeme tasarlarken, dikey yer değiştirmenin kodun izin verdiği maksimum değerden az olup olmadığını kontrol etmeliyiz. Avustralya Standartları maksimum hizmet verilebilirlik dikey yer değiştirmesini belirledi \(\çatlamak{L}{250}= frac{6000mm}{250}=24.0 mm\).
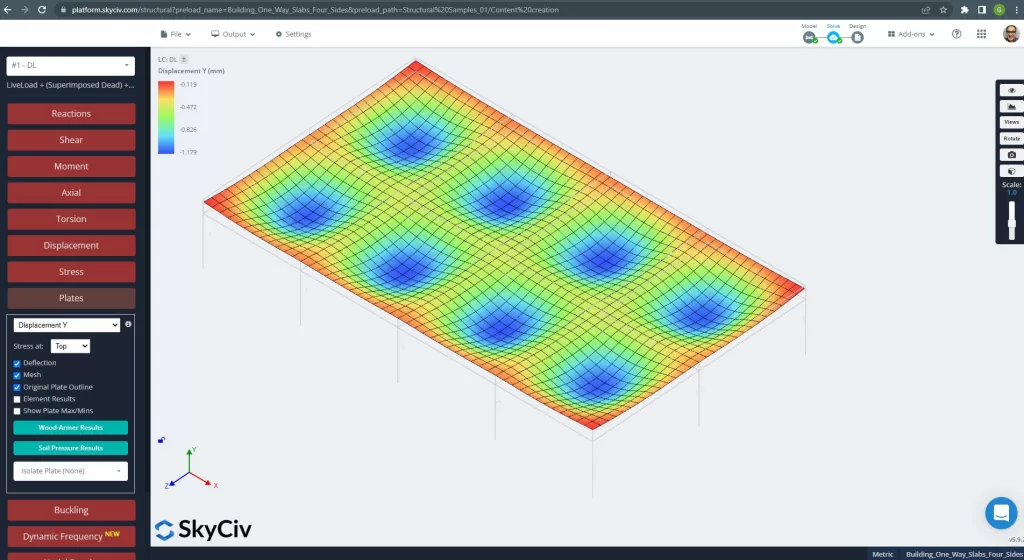
Figür 25. Izgara döşeme sisteminde Dikey Yer Değiştirme. (Yapısal 3D, SkyCiv Bulut Mühendisliği).
Yukarıdaki görüntü bize dikey yer değiştirmeyi veriyor. Maksimum değer -1,179 mm'dir ve izin verilen maksimum değer olan -24 mm'den azdır. Bu nedenle, levhanın sertliği yeterli.
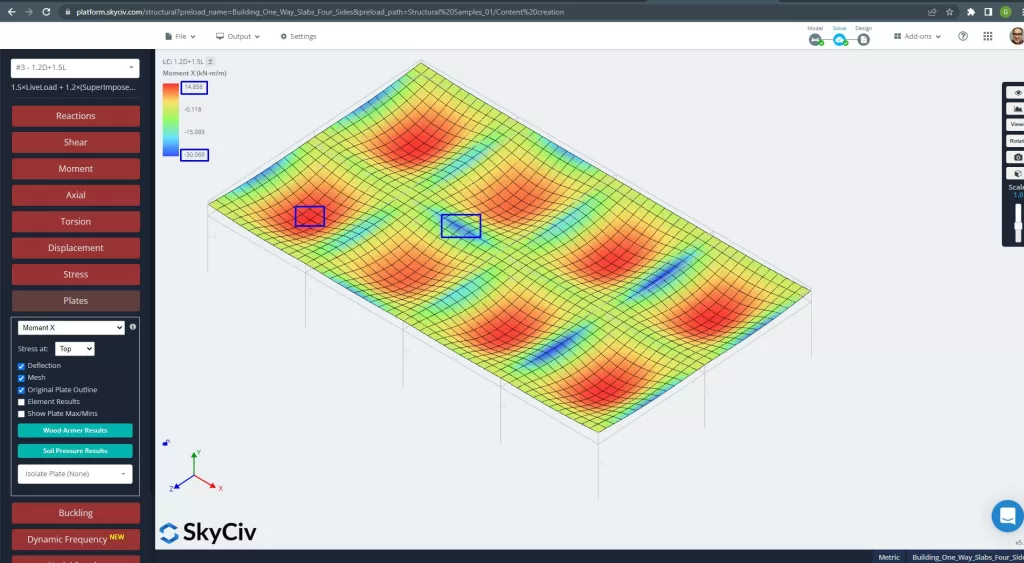
Figür 26. Plakaların X yönündeki momentleri. (Yapısal 3D, SkyCiv Bulut Mühendisliği).
Görüntüler 27 ve 28 her ana yöndeki eğilme momentinden oluşur. Moment dağılımı ve değerlerinin alınması, onların tasarımı ve analizi, SkyCiv, toplam çelik donatı alanını elde edebilir.
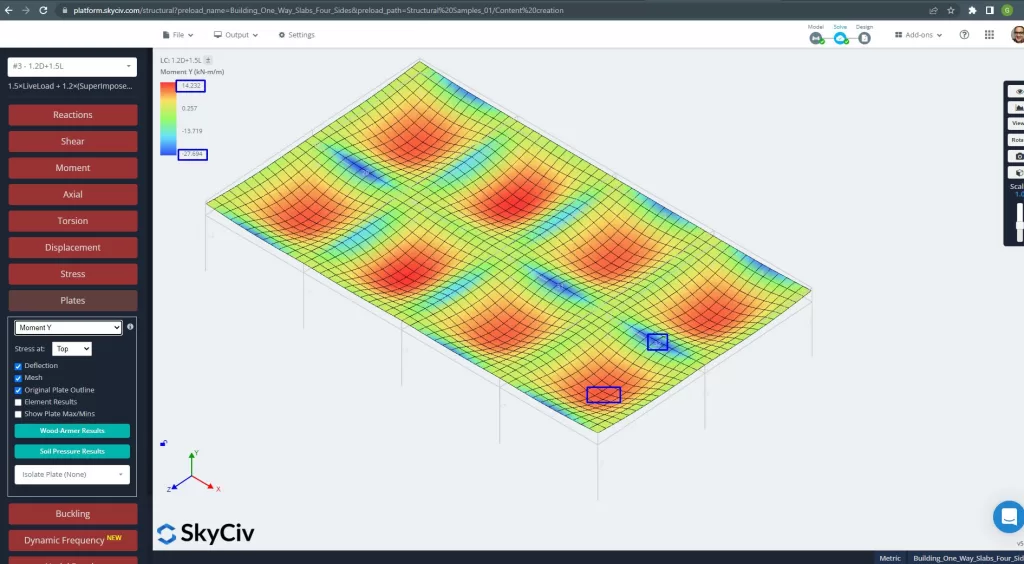
Figür 27. Plakaların Y yönündeki momentleri. (Yapısal 3D, SkyCiv Bulut Mühendisliği).
Çelik donatı alanları:
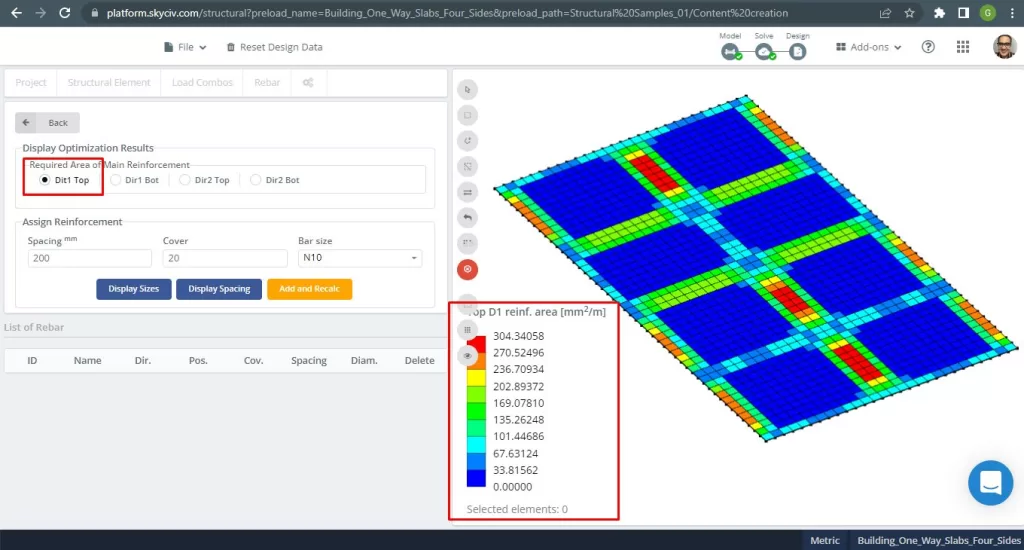
Figür 28. Yönde Üst Çelik İnşaat Demiri Takviyesi 1. (Yapısal 3D, SkyCiv Bulut Mühendisliği).
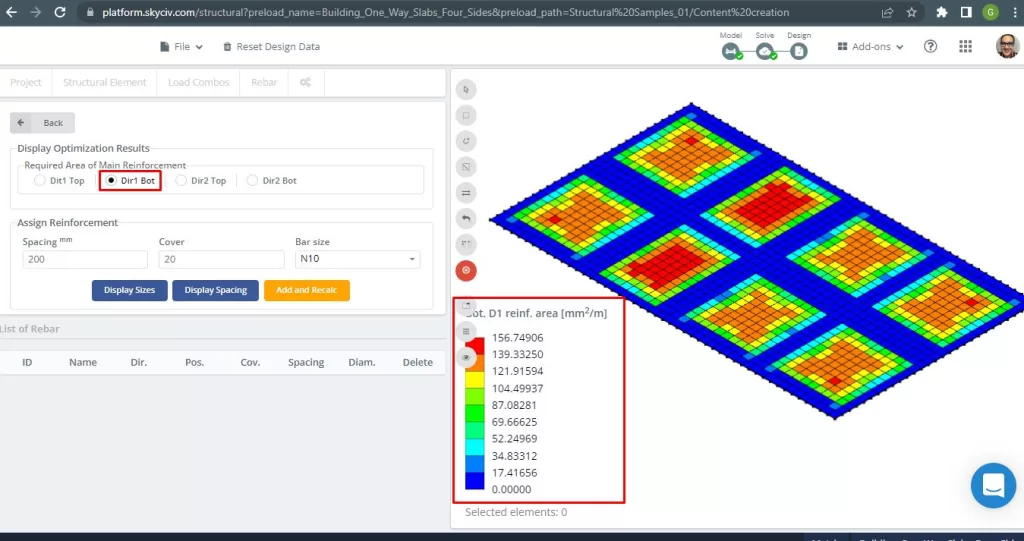
Figür 29. Yönde Alt Çelik İnşaat Demiri Takviyesi 1. (Yapısal 3D, SkyCiv Bulut Mühendisliği).
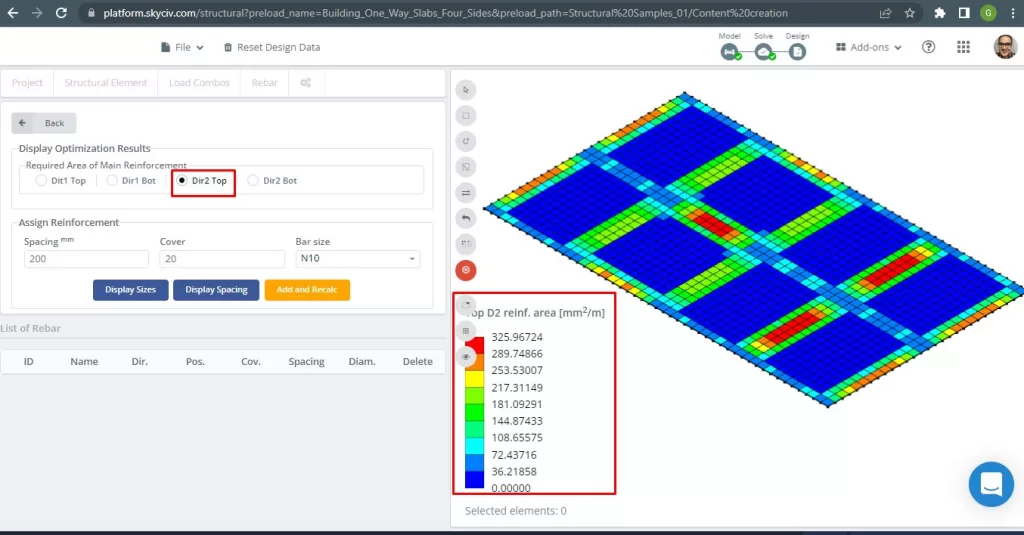
Figür 30. Yönde Üst Çelik İnşaat Demiri Takviyesi 2. (Yapısal 3D, SkyCiv Bulut Mühendisliği).
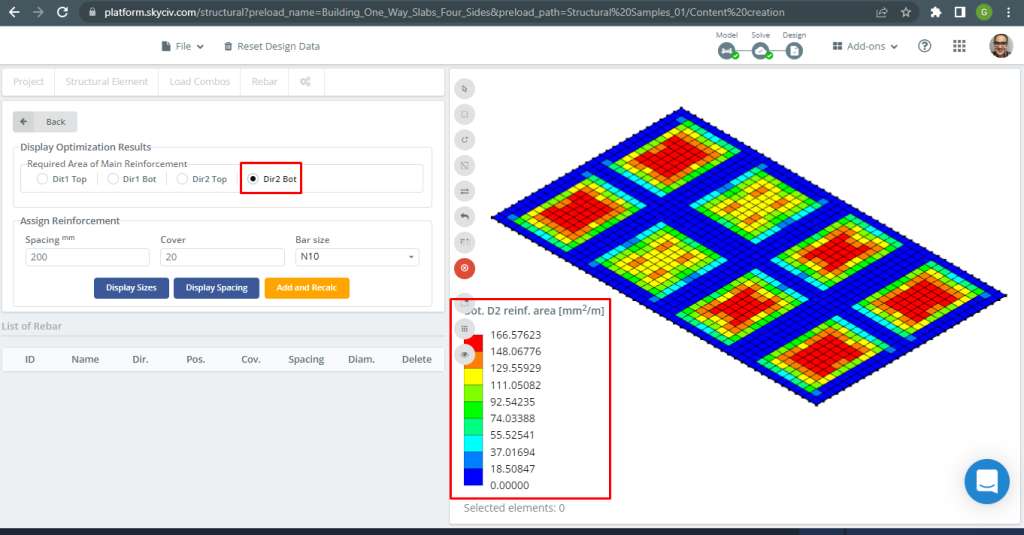
Figür 31. Yönde Alt Çelik İnşaat Demiri Takviyesi 2. (Yapısal 3D, SkyCiv Bulut Mühendisliği).
Sonuç karşılaştırması
Bu tek yönlü döşeme tasarımı örneğindeki son adım, S3D analizi ve elle yapılan hesaplamalarla elde edilen çelik inşaat demiri alanını karşılaştırmaktır..
X yönü için inşaat demiri çeliği
| Momentler ve çelik alan | Dış Negatif Sol | Dış Pozitif | Dış Negatif Sağ | İç Negatif Sol | İç Pozitif | İç Negatif Sağ |
|---|---|---|---|---|---|---|
| \(bir_{Aziz, El Hesapları} {mm^2}\) | 334.8214 | 334.8214 | 335.08233 | 334.821 | 334.8214 | 334.8214 |
| \(bir_{Aziz, S3D} {mm^2}\) | 289.75 | 149.35 | 325.967 | 325.967 | 116.16 | 217.311 |
| \(\Delta_{fark}\) (%) | 13.461 | 55.39 | 2.720 | 2.644 | 65.307 | 35.0964 |
Y yönü için inşaat demiri çeliği
| Momentler ve çelik alan | Dış Negatif Sol | Dış Pozitif | Dış Negatif Sağ | İç Negatif Sol | İç Pozitif | İç Negatif Sağ |
|---|---|---|---|---|---|---|
| \(bir_{Aziz, El Hesapları} {mm^2}\) | 334.821 | 334.821 | 334.821 | 334.821 | 334.821 | 334.821 |
| \(bir_{Aziz, S3D} {mm^2}\) | 270.524 | 156.75 | 304.34 | 304.34 | 156.75 | 270.52 |
| \(\Delta_{fark}\) (%) | 19.203 | 53.184 | 9.104 | 9.104 | 53.184 | 19.204 |
Pozitif momentler açısından fark biraz yüksektir ve bunun nedeni, Plaka Sonlu Elemanlar Analizi Sonuçlarını ve donatı çeliği bükme hesaplamalarını etkileyen yüksek burulma sertliğine sahip kirişlerin varlığı olabilir..
SkyCiv'de yeniyseniz, Kaydolun ve yazılımı kendiniz test edin!
Referanslar
- Porsuk-Chaye Loo & Sanual Hug Chowdhury , “Betonarme ve Öngerilmeli Beton”, 2ikinci baskı, Cambridge Üniversitesi Yayınları.
- Bazan Enrique & Meli Piralla, “Yapıların Sismik Tasarımı”, 1ed, TEMİZLEMEK.
- Avustralya Standardı, Beton yapılar, GİBİ 3600:2018


