Оглавление

• Обзор – Что такое момент инерции
• пример – Как рассчитать момент инерции
• Формулы и уравнения
• Калькуляторы
• Практические вопросы

Обзор – Что такое момент инерции?

В контексте строительного проектирования, Момент инерции — это свойство сечения, используемое для определения способности элемента конструкции сопротивляться изгибающим и скручивающим силам.. Обычно это довольно хороший показатель жесткости и прочности секций под нагрузкой.. Более высокий момент инерции означает, что конструкция лучше сопротивляется изгибу и отклонению., что делает его важным фактором при проектировании балок, столбцы, и другие несущие детали. В качестве примечания: Иногда это неправильно определяют как второй момент инерция, однако это неправильно. Другие названия момента инерции:: момент инерции площади, или второй момент результаты вместе с преобразованными результатами раздела.

пример – Как рассчитать момент инерции сечения балки

Прежде чем найти момент инерции сечения балки (также известный как второй момент площади сечения балки), его центроид (или центр масс) должен быть известен. Например, если момент инерции сечения относительно его горизонтали (XX) ось требовалась тогда вертикальная (и) сначала потребуется центроид (Пожалуйста, просмотрите наши руководства по вычисление центроида сечения балки и вычисление статического/первого момента площади).

Прежде чем мы начнем, если вы искали наш Калькулятор свободного момента инерции пожалуйста, нажмите на ссылку, чтобы узнать больше. Это вычислит центр тяжести, момент инерции, и другие результаты и даже покажут вам пошаговые расчеты! Но сейчас, давайте посмотрим на пошаговое руководство и пример того, как рассчитать момент инерции:

шаг 1: Сегментируйте сечение балки на части

При расчете площади момента инерции, мы должны рассчитать момент инерции меньших сегментов. Попробуйте разбить их на простые прямоугольные секции. Например, рассмотрите раздел I-луча ниже, который также был показан в нашем учебнике по центроидам. Мы решили разделить этот раздел на 3 прямоугольные сегменты:

 

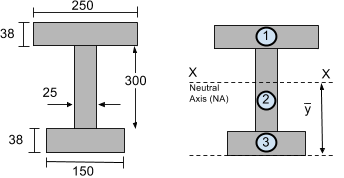
шаг 2: Рассчитать нейтральную ось (Не Доступно)

Нейтральная ось (Не Доступно) или горизонтальная ось ХХ находится в центре тяжести или центре масс. В нашем учебнике по центроидам, ранее было установлено, что центр тяжести этого участка 216.29 мм от нижней части секции – это описано в нашем как найти центр тяжести фигуры Как решить ферменную конструкцию, используя метод сечений. Их также можно просто рассчитать из нашего Эта статья проведет вас через простой процесс расчета центроида или из общего уравнения центроида.

Вычисление центроида, или нейтральная ось, имеет важное значение в как рассчитать момент инерции балки, так как это ось, на которую действует момент инерции.

шаг 3: Рассчитать момент инерции

Для расчета общего момента инерции сечения нам нужно использовать “Теорема о параллельной оси”:

Так как мы разделили его на три прямоугольные части, мы должны рассчитать момент инерции каждого из этих участков. Широко известно, что момент уравнения инерции прямоугольника относительно его оси центроида просто:

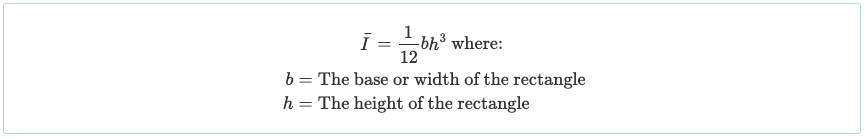
Момент инерции других форм часто указывается на лицевой / оборотной стороне учебников или в этом руководстве. момент инерции формы. Однако прямоугольная форма очень распространена для секций балки, так что, наверное, стоит запомнить.

Теперь у нас есть вся информация, необходимая для использования “Теорема о параллельной оси” и найти общий момент инерции сечения двутавровой балки. В наш момент инерции пример:

Итак, у нас есть руководство по расчету площади момента для сечений балок.. Этот результат имеет решающее значение в проектировании конструкций и является важным фактором в отклонении луча. Мы надеемся, что вам понравился урок, и с нетерпением ждем ваших комментариев.. Чтобы получить больше информации, посетите наш урок на Формула момента инерции и уравнения.

Формулы и уравнения

Каждый тип раздела (прямоугольный, Я луч, круговое) имеет свою формулу для быстрого расчета. Это упрощенные уравнения, которые позволяют инженерам быстро и легко рассчитать это важное свойство..

Уравнения представляют собой упрощенное выражение описанных выше шагов.. Например, формула момента инерции полого прямоугольника по сути представляет собой МВД большей секции. – чем меньше (внутренний) раздел:

[математический] \dfrac{бх ^ 3}{12} – \dfrac{b_1h_1 ^ 3}{12} [математический]

SkyCiv собрал удобный ресурс для общего Формула момента инерции.

Калькуляторы

Существует множество способов расчета момента инерции., одним из которых является использование программного обеспечения, чтобы сделать процесс проще.

SkyCiv Раздел Строитель Это полнофункциональный инструмент для проектирования секций, который выходит далеко за рамки калькулятора момента инерции.. Он также покажет вам пошаговые расчеты того, как найти момент инерции.:

альтернативно, вы можете увидеть результаты нашего Калькулятор свободного момента инерции проверить свою работу. Это позволит вычислить все свойства вашего поперечного сечения и является полезным справочным материалом для расчета центроида., Площадь, и момент инерции секций вашей балки! Дополнительным преимуществом является то, что вы также можете включить радиус в углах., для более точных расчетов.

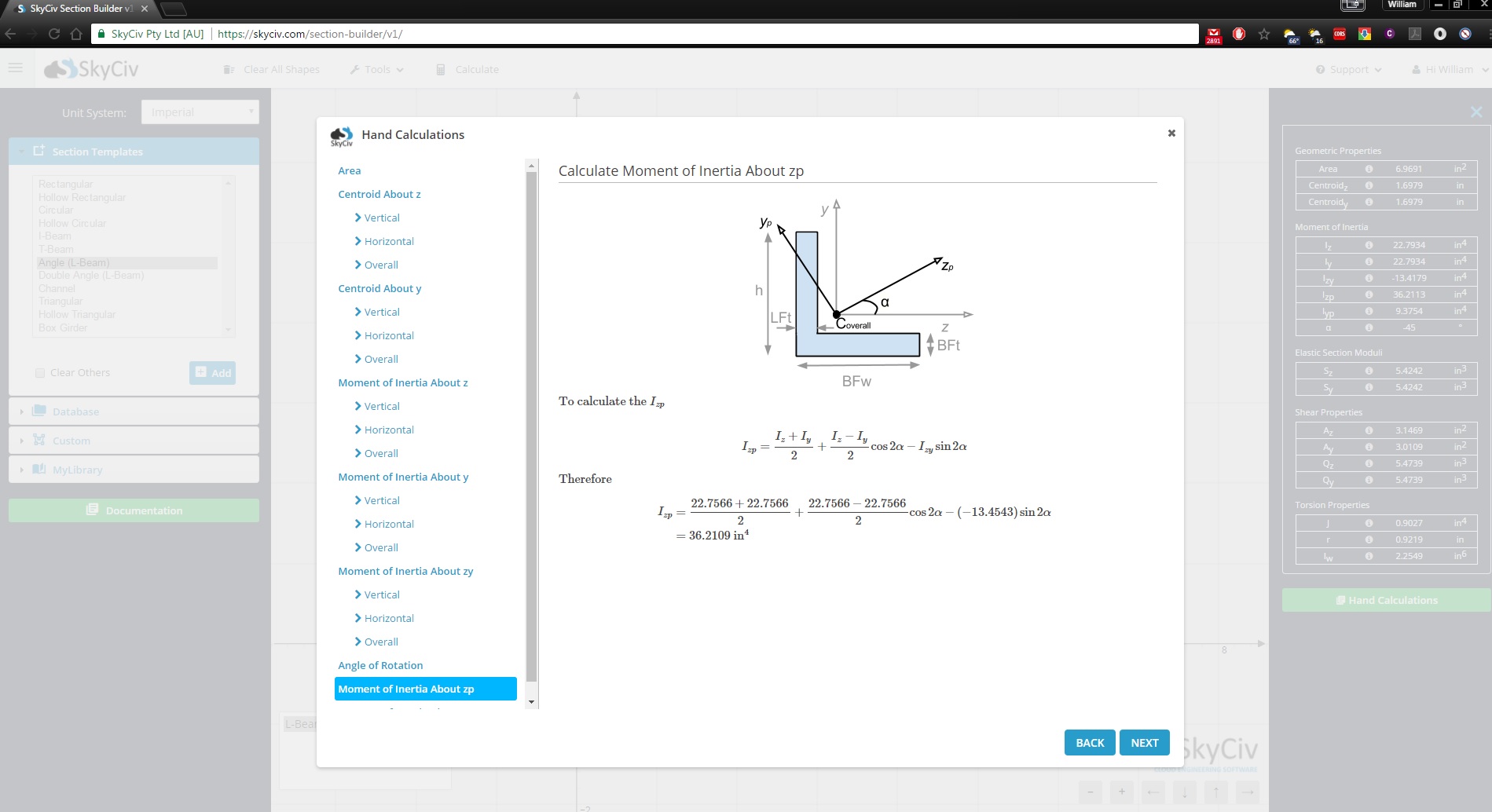
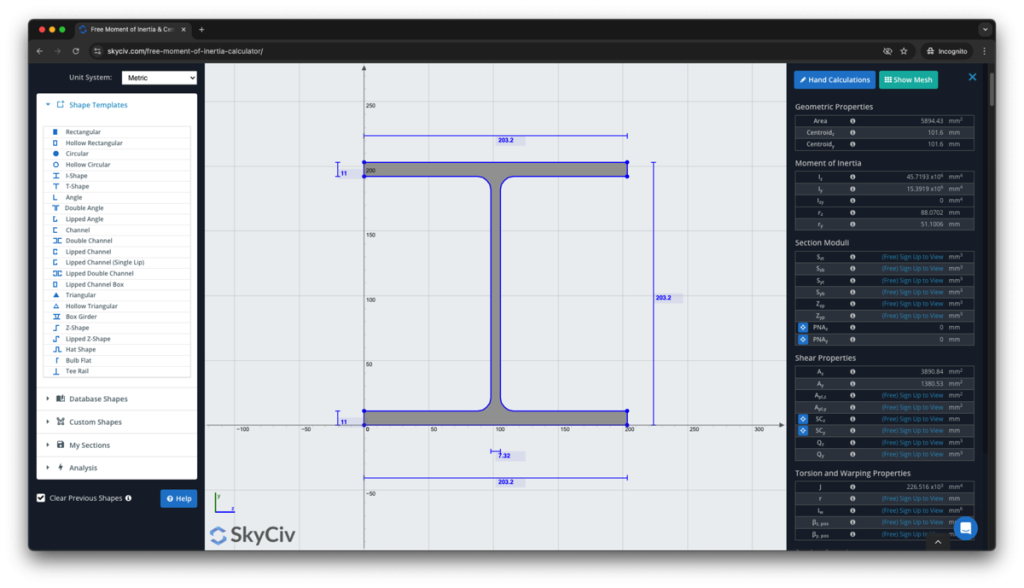
Зарегистрируйтесь сегодня, чтобы узнать больше о программном обеспечении SkyCiv, или забронируйте БЕСПЛАТНАЯ ДЕМО чтобы получить помощь с вашими инженерными проектами для существующих пользователей!

Дополнительно, SkyCiv имеет бесплатный Калькулятор свойств раздела как часть библиотеки быстрого дизайна. Это упрощенный инструмент, но также рассчитает момент инерции обычных форм сечения..

Зарегистрироваться Сегодня

Практические вопросы

Как решить ферменную конструкцию, используя метод сечений 1: Прямоугольное сечение

Проблема: Рассчитайте момент инерции (Икс и Айу) для прямоугольного сечения шириной (б) из 200 мм и высота (час) из 300 мм.

Решение: Формулы момента инерции прямоугольника::

[математический] \dfrac{бх ^ 3}{12} [математический]Взаимодействие с другими людьми

Подстановка данных значений:

• б=200 мм
• высота=300 мм

Для Икса:

[математический] \dfrac{бх ^ 3}{12} = dfrac{200(300^3)}{12} = 450×10^6 мм^4 ​ [математический]Взаимодействие с другими людьми

Для Иии:

[математический] \dfrac{бх ^ 3}{12} = dfrac{300(200^3)}{12} = 200×10^6 мм^4 ​ [математический]Взаимодействие с другими людьми

Как решить ферменную конструкцию, используя метод сечений 2: I-Beam

Проблема: Рассчитаем момент инерции главной оси. (икс) сечения двутавра со следующими размерами:

• Ширина верхнего фланца (TFW) знак равно 6 в
• Толщина верхнего фланца (Tft) знак равно 0.43 в
• Глубина секции = 6 в
• Толщина полотна (вес) знак равно 0.29 в
• Ширина нижнего фланца (BFW) знак равно 6 в
• Толщина нижнего фланца (BFT) знак равно 0.43 в

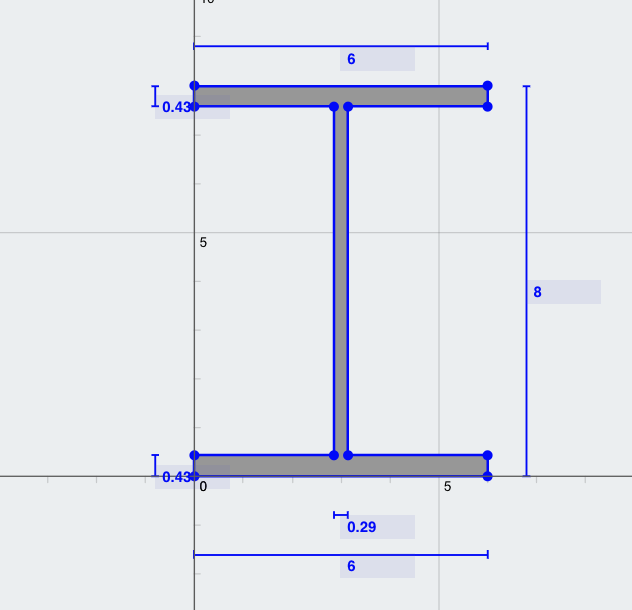
Решение:

[математический] Я_{хх} знак равно 82.8 в^4​ [математический]Взаимодействие с другими людьми