Определение частотного анализа?
При проектировании зданий, есть два виды нагрузок рассматривать: статический и динамический. Для первого, необходимо только рассчитать непосредственную реакцию конструкции на действующие постоянные нагрузки в виде перемещений и напряжений.. Это может быть достигнуто с помощью жесткости или метода конечных элементов..
В случае динамического анализа, сложнее рассмотреть диапазон возможных вариаций отклика конструкции из-за зависящих от времени нагрузок. Следовательно, некоторые новые инструменты или функции становятся необходимыми для включения в анализ. Так, частотный анализ, фундаментальный метод в механике вибрации, возникает.
Этот метод позволяет получить изменение во времени движения конструкции из-за приложенных динамических нагрузок.. Более конкретно, это подразумевает использование естественных свойств вибрации конструктивной системы для расчета внутренних сил., смещения, проблемы со стабильностью, и т.д.
Для получения дополнительной информации по теме, мы предлагаем прочитать статью SkyCiv, в которой кратко объясняется, как выполнить Динамический частотный анализ с использованием SkyCiv Программное обеспечение для структурного анализа.
Почему частотный анализ актуален для проектирования?
Лучший способ измерить важность частотного анализа в проекте — это наблюдать за некоторыми конструкциями, которые вышли из строя из-за плохого динамического поведения.. Один из самых известных мостов в Северной Америке - Tacoma Narrows., который окончательно разрушился после продолжительных периодических колебаний, вызванных ветром. На следующих изображениях показано увеличенное смещение вдоль моста непосредственно перед обрушением., ориентирован в первую очередь на проезжую часть:

Рисунок я. Боковые крутильные колебания в Tacoma Narrows Bridge

Рисунок II. Увеличено смещение на Мосту перед обрушением.

Рисунок III. Катастрофический обвал моста
В данном случае исследование, не был проведен надлежащий частотный анализ, и конструкция не была надлежащим образом спроектирована для учета собственной частоты конструкции..
Простой маятник
Частотный анализ изучает различные формы, которые принимает структура, когда она подвергается внешним динамическим воздействиям.. Вот почему вы получаете несколько разных режимы. Затем с помощью этих форм, мы можем установить размеры элементов конструкции через внутренние силы, необходимые для обеспечения равновесия.
Прежде чем углубляться в технические и математические аспекты частотного анализа, просмотрите следующую простую систему маятниковой колонны, показанную на рисунке iv..
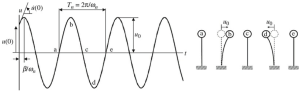
Рисунок IV. Динамический отклик маятниковой системы со свободными колебаниями
Используя простой анализ, как показано на последнем изображении, мы можем определить движение верхней массы маятниковой колонны каждый раз. Основная цель этой статьи — провести частотный анализ для двух типичных случаев., с одной и несколькими степенями свободы.
Единая степень свободы
Этот частный случай является наиболее простым для динамического анализа.. Поведение описывается с помощью закона равновесия Даламбера, расширение второго закона Ньютона.
На следующем рисунке показаны элементы системы SDOF., жесткость (К), демпфирование (с), и массовый источник (м) для сил инерции. Изменяющаяся во времени внешняя сила, приложенная к массе, представлена \({п(T)}\).
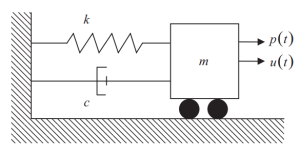
фигура 1. Единая степень свободы (СДОФ) Система. (Чаша, 2017, страница 56)
Все элементы должны удовлетворять условию динамического равновесия:
\({м}{\точка{U}}+{с}{\точка{U}}+{К}{U}знак равно{п(T)}\)
Это линейное дифференциальное уравнение второго порядка, и его решение имеет две составляющие:
\({U(T)}знак равно{U}_{час}(T)+{U}_{п}(T)\)
куда:
- \({U(T)}\) абсолютное смещение.
- \({U}_{час}(T)\) является однородным раствором, как правило, в случае свободных колебаний.
- \({U}_{п}(T)\) является частным решением в соответствии с приложенным возбуждением.
Мы сосредоточимся только на однородном решении для описания вибрационного поведения и наиболее важных динамических характеристик конструкции..
Определим следующие термины:
\({\омега_{N}}знак равно{\SQRT(\гидроразрыва {К}{м})}\) Угловая частота
\({\xi}знак равно{\гидроразрыва{с}{{2}{м}{\omega_n}}}знак равно{\гидроразрыва{с}{{2}{\SQRT(\гидроразрыва {К}{м})}}}\) Доля критического демпфирования
Когда доля критического демпфирования меньше 1, корпус вибрации будет недостаточно демпфирован; то есть, будут завершены циклы, прежде чем движение прекратится.
Решение имеет следующий общий вид
\({Эм-м-м}знак равно{е ^{{-\xi}{\омега_{N}}{T}}}{[{А}{потому что}{\omega_d}{T}+{В}{без}{\omega_d}{T}]}\)
куда:
- A и B — константы интегрирования, зависящие от начальных условий движения..
- \({\omega_d}знак равно{\omega_n}{\SQRT({{1}-{\xi^2}})}\) - затухающая угловая частота
После оценки констант A и B, общее решение для незатухающего случая:
\({Эм-м-м}знак равно{е ^{{-\xi}{\омега_{N}}{T}}}{[{u_0}{потому что}{\omega_d}{T}+{\гидроразрыва{{\точка{u_0}}+{\xi}{\omega_n}{u_0}}{\omega_d}}{без}{\omega_d}{T}]}\)
куда:
- \({u_0}\) это массовое начальное перемещение
- \(\точка{u_0}\) начальная скорость массы
Если построить решение с некоторыми значениями начальных условий, мы получим следующую фигуру.
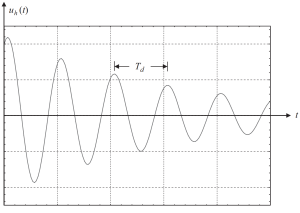
фигура 2. Смещение приводит к однородной части решения в докритическом демпфированном случае.. (Чаша, 2017, страница 58)
В другом случае, важно проанализировать, что происходит, когда доля критического демпфирования имеет значение 1. \({\xi}=1). Это условие подразумевает структуру с полным демпфированием.
Используемое уравнение
\({Эм-м-м}знак равно{е ^{{-\омега_{N}}{T}}}{\{u_0+({\точка{u_0}}+{\omega_n}{u_0}){T}}\}\)
И их график, показывающий разные случаи начальных условий, показан на следующем изображении..
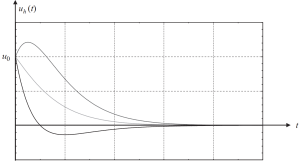
фигура 3. Смещение приводит к однородной части решения в случае критического демпфирования.. (Чаша, 2017, страница 58)
Параметры ответа
Предыдущий раздел помог нам определить решение для свободной динамической вибрации в системе SDOF.. Двумя основными параметрами являются собственная частота \(\omega_n\) который указывает, как конструкция будет вибрировать сама по себе, и доля критического демпфирования \(\xi), определяющее скорость в затухающих колебаниях.
В общем-то, конструкции имеют низкое демпфирование с максимальным значением \(\xi)=10 %. Если мы оценим демпфированную собственную частоту, используя это значение, результат \({\omega_d}=0,995{\omega_n}\). Так, рекомендуется использовать \({\omega_d}{\толстыйприблизительно}{\omega_n}\).
Мы можем обобщить динамические свойства в следующей таблице..
| Угловая частота (рад/с) | Собственная частота (Гц) | Естественный период (s) | |
|---|---|---|---|
| Угловая частота \({\omega_n}\) | \({\omega_n}\) | \(2{\число Пи}{f_n}\) | \(\гидроразрыва{2{\число Пи}}{T_n}\) |
| Собственная частота \({f_n}\) | \(\гидроразрыва{\omega_n}{2{\число Пи}}\) | \(f_n\) | \(\гидроразрыва{1}{T_n}\) |
| Естественный период \({T_n}\) | \(\гидроразрыва{2{\число Пи}}{\omega_n}\) | \(\гидроразрыва{1}{f_n}\) | \(T_n\) |
Стол 1. Связь между угловой частотой, собственная частота, и период (Чаша, 2017, страница 60)
Несколько степеней свободы
Когда в конструкции существует много масс, мы должны определить несколько координат, чтобы описать положение в любое время для этих масс. Один конкретный и очевидный пример показан на следующем рисунке., состоящий из сложного маятника, где необходимы разные углы для определения положения в каждый момент движения.
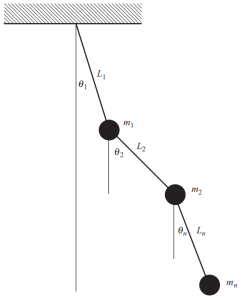
фигура 4. Маятник с несколькими массами. (Чаша, 2017, страница 53)
В этой секции, мы анализируем структуры’ общая динамическая характеристика с использованием расширения частотного анализа свойств для нескольких степеней свободы.
Крайне важно знать о процессе моделирования при работе с реальной структурой.. На следующих изображениях показаны необходимые шаги для построения математической модели, готовой к применению частотного анализа для описания ее динамического отклика..
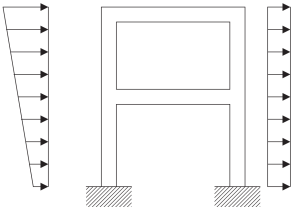
фигура 5. Физическая модель континуального структурного каркаса. (Чаша, 2017, страница 23)
Первый шаг включает в себя объединение масс на каждом уровне пересечения балок и колонн.. Каждый узел имеет три возможных движения, два линейных перемещения, и один оборот. Быть последовательным в анализе, необходимо учитывать массы и полярные инерционные свойства.
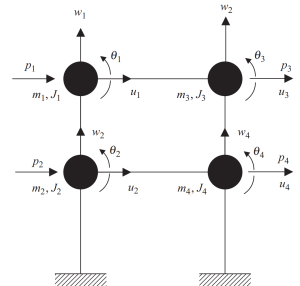
фигура 6. Сосредоточенные массы в узлах со степенями свободы перемещения и вращения. Дискретная система. (Чаша, 2017, страница 23)
Метод статической конденсации может помочь уменьшить сложность анализа., пренебрегая вращательной и поступательной инерцией.
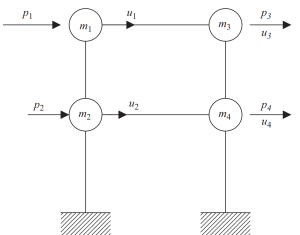
фигура 7. Статическое сгущение степеней свободы только к горизонтальному перемещению. (Чаша, 2017, страница 23)
На последнем шаге, мы можем объединить только два узла горизонтального движения для этого примера кадра.
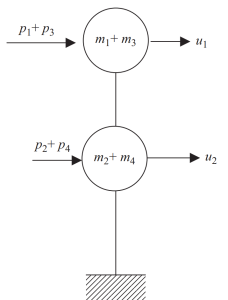
фигура 8. Окончательное статическое сгущение до двух узлов и степень свободы горизонтального смещения. (Чаша, 2017, страница 24)
Как мы делали в предыдущем разделе с системой SDOF., разработаем решение уравнения движения для нескольких степеней свободы.
Уравнение движения записывается в матричной форме как
\([M]\{\точка{U}\} + [С]\{\точка{U}\}+[К]\{ты }знак равно{п(T)}\)
куда:
- \([M]\) матрица масс
- \([С]\) – матрица демпфирования Кулона
- \([К]\) это матрица жесткости
Мы должны изучить решение для свободных колебаний, чтобы получить параметры отклика. К системе не применяется демпфирование и сила, оцениваются только начальные условия.
\([M]\{\точка{U}\} +[К]\{ты }знак равно{0}\)
По аналогии с первым случаем для SDOF, мы можем проверить синусоидальное решение формы.
\({U(T)}знак равно{\фи}{({а }{потому что}{\омега}{T}+{б}{без}{\омега}{T})}\)
\({\точка{U}{(T)}}знак равно{-{\омега}^ 2}{\фи}{({а }{потому что}{\омега}{T}+{б}{без}{\омега}{T})}\)
в котором вектор \(\фи) вектор формы, не зависящий от времени. Коэффициенты “а ” и “б” константы, полученные при оценке начальных условий.
После подстановки обоих выражений для тестового решения в уравнение движения, мы получаем линейную задачу собственных значений-векторов:
\([К]{\фи}знак равно{{\омега}^ 2}[M]{\фи}\)
куда:
- \({{\омега}^ 2}\) множество собственных значений
- \({\фи}\) это набор собственных векторов
Решение этой классической задачи для примера рамы на последних рисунках показывает, как будут вибрировать массы.. Это означает, что каждая масса будет двигаться в горизонтальном направлении в соответствии со значением собственных векторов.
Посмотрите на следующее изображение этого поведения.
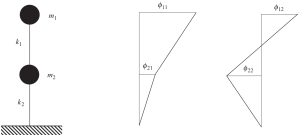
Рисунок №9. Частотный анализ, показывающий результаты двух собственных векторов. (Чаша, 2017, страница 135)
SkyCiv Структурная 3D
Выполняйте частотный анализ ваших конструкций с помощью SkyCiv Структурная 3D. Зарегистрируйтесь сегодня, чтобы начать!
Ссылки:
- Эдуардо Каусель, (2017). “Расширенная структурная динамика” 1первое издание, Издательство Кембриджского университета

