Bir Kafes Sisteminin Eksenel Kuvvetlerini Eklem Yöntemi Kullanarak Hesaplama?
Bu öğreticide, Bir kafes sistemi veya yapısındaki iç eleman kuvvetlerini hesaplamak için birleşim yönteminin nasıl kullanılacağını açıklayacağız..
Bu kuvvetler Eksenel Kuvvetler olarak bilinir ve kafes analizinde çok önemlidir.. Makalemizde ne demet gördüğünden emin değilseniz – Kafes nedir. Eklem Yöntemi, temel olarak "eklemlerin her birine’ (üyelerin buluştuğu yer) ve çözmek için statik denklemler uygulamak.
Harika olan şey, SkyCiv Kafes bunu sizin için otomatik olarak yapıyor. Kendi kafes kirişlerinizi modelleyin ve yazılım, bağlantı yöntemiyle adım adım çalışarak etkileşimli adım gösterecektir.!
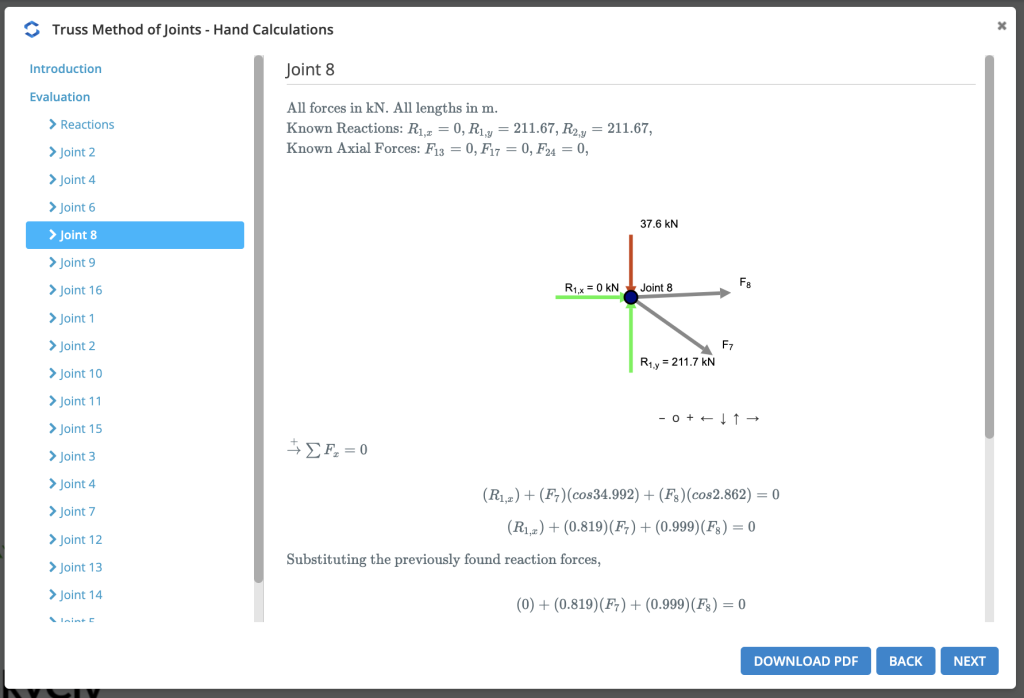
Adım 1: Desteklerdeki Reaksiyonları Hesaplayın
İlk, hesaplıyoruz desteklerdeki tepkiler. Basit bir örneğe bakarak başlayacağız. 5 üye makas sistemi:
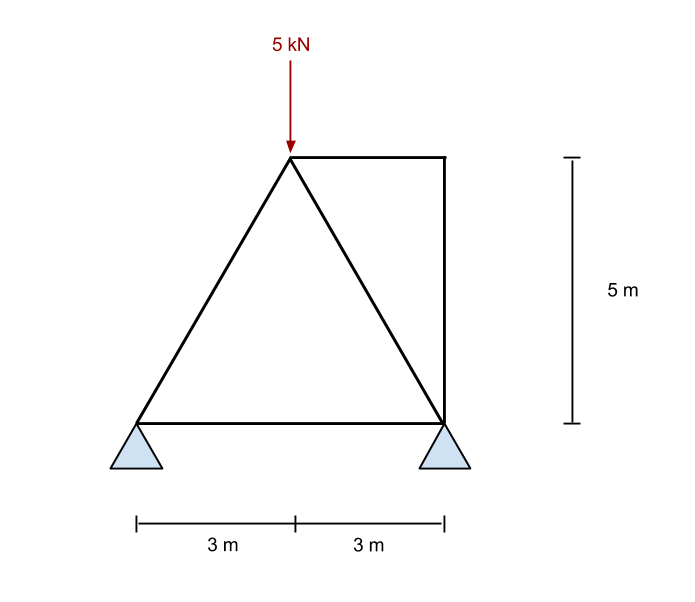
hesaplamak için bükülme anı bu kafes sisteminde, önce sol reaksiyondaki anların toplamını sıfır olarak alıyoruz. Bunu tüm üyeleri görmezden gelerek ve sadece yapıdaki güçlere ve desteklere bakarak yapıyoruz.. Bu, önceki eğitimimizde Bükülme Momenti Reaksiyonlarında kullanılan yöntemle aynıdır..
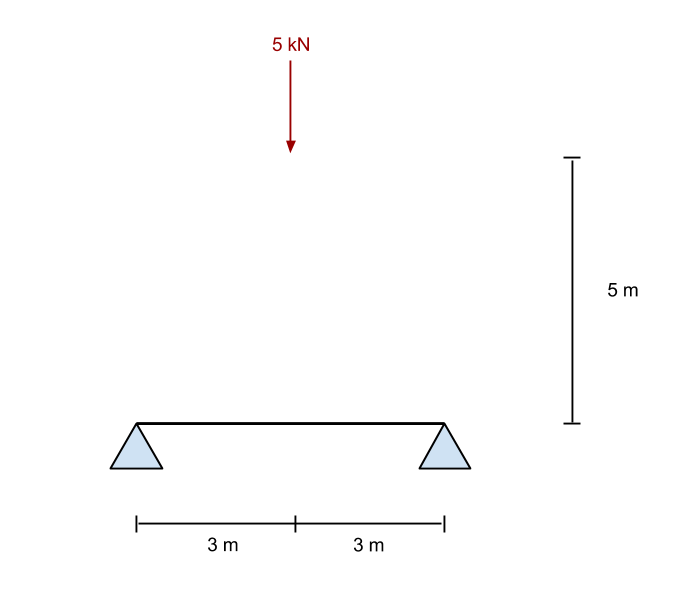
Yukarıdaki denklemlerden, B noktasındaki reaksiyon kuvvetini çözeriz (doğru destek). Örneğimizde, bu işe yarıyor 2.5 yukarı yönde kN. Şimdi, y'deki kuvvetlerin toplamını alırsak (dikey) yön, A desteğini bulduk (sol destek) olarak da verilir 2.5 kN.
Adım 2: Desteklerden birini düşünün:
Artık reaksiyon kuvvetlerine sahip olduğumuza göre, bu kafes yapısının geri kalanının analizine başlayabiliriz.. birinci olarak, bilinen güçlerimizden birine bakıyoruz – bu durumda, sol destek tepkisini ele alacağız +2.5 kN. Bu kuvvetin bu noktada oluştuğunu bildiğimiz için, sadece bu noktayı izole olarak ele alacağız. Bu işlemi birkaç kez tekrarlıyoruz, Bu nedenle, kafes yapılarda eksenel kuvvetlerin nasıl çözüleceğine dair iyi bir kavrayışa sahip olmak için süreci uygulamak ve öğrenmek önemlidir.. Ve yine, destekteki ilk noktayı düşünün:
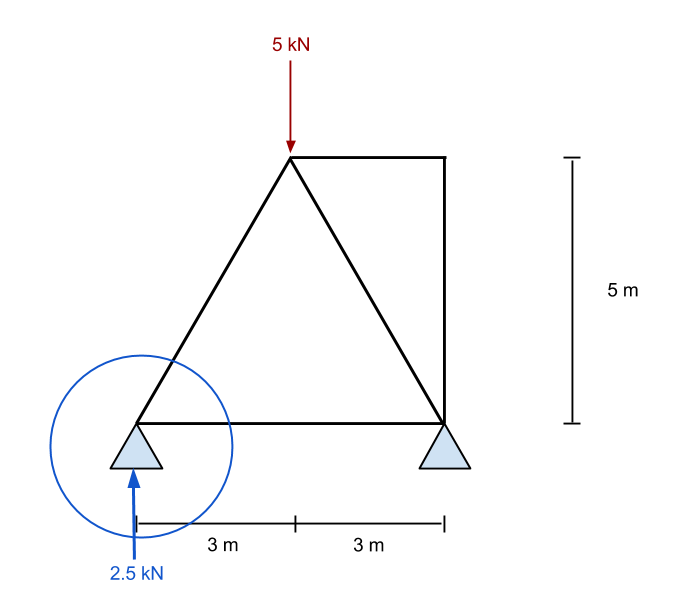
Bu noktaya yakınlaştırma, bu noktada hareket eden tüm bilinen güçleri görüyoruz. Statikten, x ve y yönündeki kuvvetlerin toplamının sıfır olması gerektiğini biliyoruz. Buna göre, Yukarı doğru bir dikey kuvvet olduğunu bilirsek, o zaman ona karşı koymak için aşağı doğru bir kuvvet olmalı. Zaten yukarı bakan bir kuvvetin değerine sahip olduğumuz için, sonra üye numarasını değerlendirmeye çalışacağız 1 ilk.
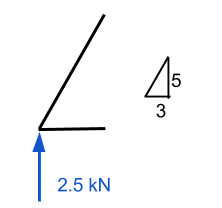
Burada vektörler hakkında biraz bilgiye ihtiyacımız var. Hem x hem de y yönü için tüm kuvvetlerin toplamının sıfır olması gerektiğini hatırlamak önemlidir.. Örneğimizde, yatay mesafe 3m iken dikey 5m – bizi yaklaşık olarak eşit hipotenüs bırakarak 5.83 m. Bunu kullanarak, üyenin normal kuvvet bileşeninin 1 eşittir (5.83)/(5) dikey kuvvetin katı 2.5 kN. Bu eşittir 2.92 Eğer nokta sabit kalacaksa kN ve ZORUNLU aşağı doğru etki eden bir kuvvet olmalıdır.
Üye 2 hemen hemen aynı şekilde hesaplanabilir. O üyeyi tanıyorsak 1 aşağı doğru hareket ediyor, o zaman bunun da sola doğru hareket etmesi gerektiğini biliyoruz. Buna göre, üye tanıyoruz 2 x yönündeki kuvvetleri korumak için noktayı sağa çeken bir kuvvet oluşturmalıdır. Bu değer şu şekilde hesaplanır: (3/5.83) x 2.92 kN ve eşittir 1.51 kN.
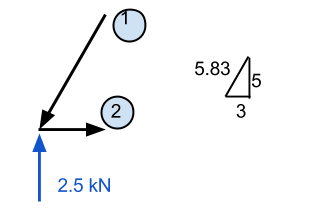
Adım 3: Başka bir noktaya git:
Kirişimizdeki ilk üyenin iç kuvvetlerini hesapladıktan sonra, Şimdi süreci tekrarlamak için başka bir noktaya bakacağız:
Tekrar, referans noktasına yaklaşacağız ve noktaya etki eden tüm bilinen kuvvetleri dikkate alacağız.:
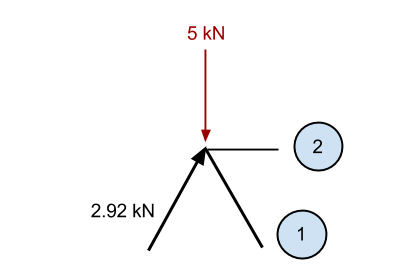
Daha önce olduğu gibi, bilinen dikey bileşeni toplarsak 2.92 kN üyesi (2.5 dikey yönde kN) ve – 5kN aşağı doğru kuvvet, o zaman aşağı yönde fazlalık var 2.5 kN (5 – 2.5). Buna göre, o üyeyi biliyoruz 1 noktayı statik tutmak için yukarı yönde bir kuvvete neden olması gerekir. Bu kuvvetin dikey bir bileşeni olmalıdır. 2.5 kN, ve önceki üye ile aynı açıda olduğu için, o zaman iç eksenel kuvvet de olmalıdır 2.92 kN.
Şimdi x yönündeki kuvvetleri ele alıyoruz. Bu noktada, üyeden gelen tüm dikey kuvvet 1 önceden hesaplanan üyenin dikey kuvvetine direniyor. Bu, x yönündeki kuvvetlerin toplamının zaten sıfır olduğu anlamına gelir. Buna göre, Üye'de güç olamaz 2 yoksa nokta dengesizleşecek ve artık statik olmayacak.
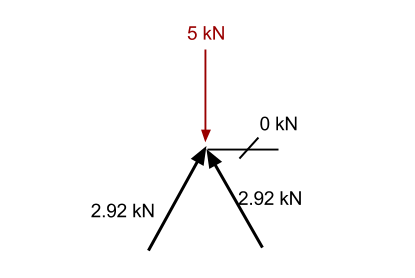
Adım 4: Başka bir noktaya git:
Bu noktaya bakıyorum, özel bir durum olduğunu görebiliriz. Bu durumda, yukarı iten herhangi bir kuvvetin olası direniş eylemi olmayacak, Noktayı statik tutmak için aşağı doğru bir kuvvet sağlayabilen başka bir üye olmadığından. Buna göre, kuvvetlerin toplamı sıfır olması gerektiğinden, bu üyenin kendisiyle ilişkili hiçbir gücü olamaz. O, bu nedenle, hiçbir gücü yoktur ve Sıfır Üye olarak bilinir.
Tekrar, x yönündeki kuvvetleri toplamaya bakarsak, x-yönünde herhangi bir kuvveti olan tek bir üye olduğunu görebiliriz. Buna göre, bu da olmalı 0 Kuvvetlerin toplamının sıfıra eşit olması için eksenel kuvvet.
Son çözüm
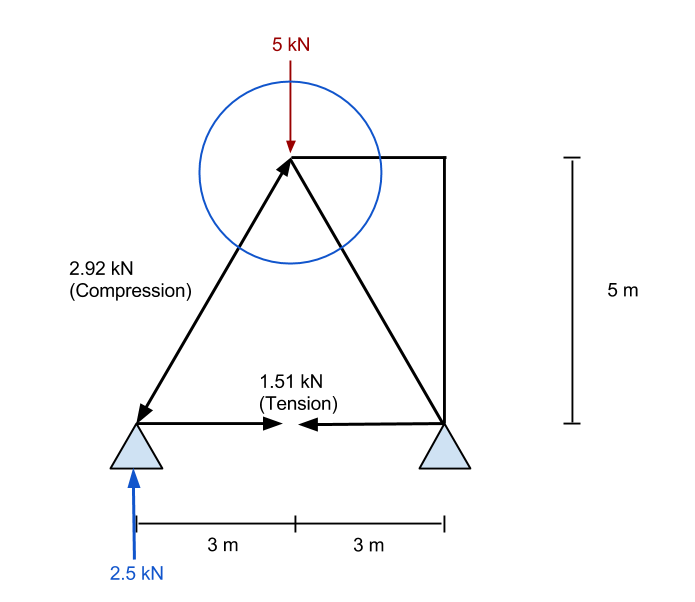
En sonunda, kirişimiz için aşağıdaki sonucu elde ederiz. Elemanın içinde ortaya çıkan tüm eksenel kuvvetleri görebiliriz ve desteklerdeki tepkiler. Aşağıdaki sonuç bizim Ücretsiz Kafes Hesaplayıcı – bir şans ver, bedava!
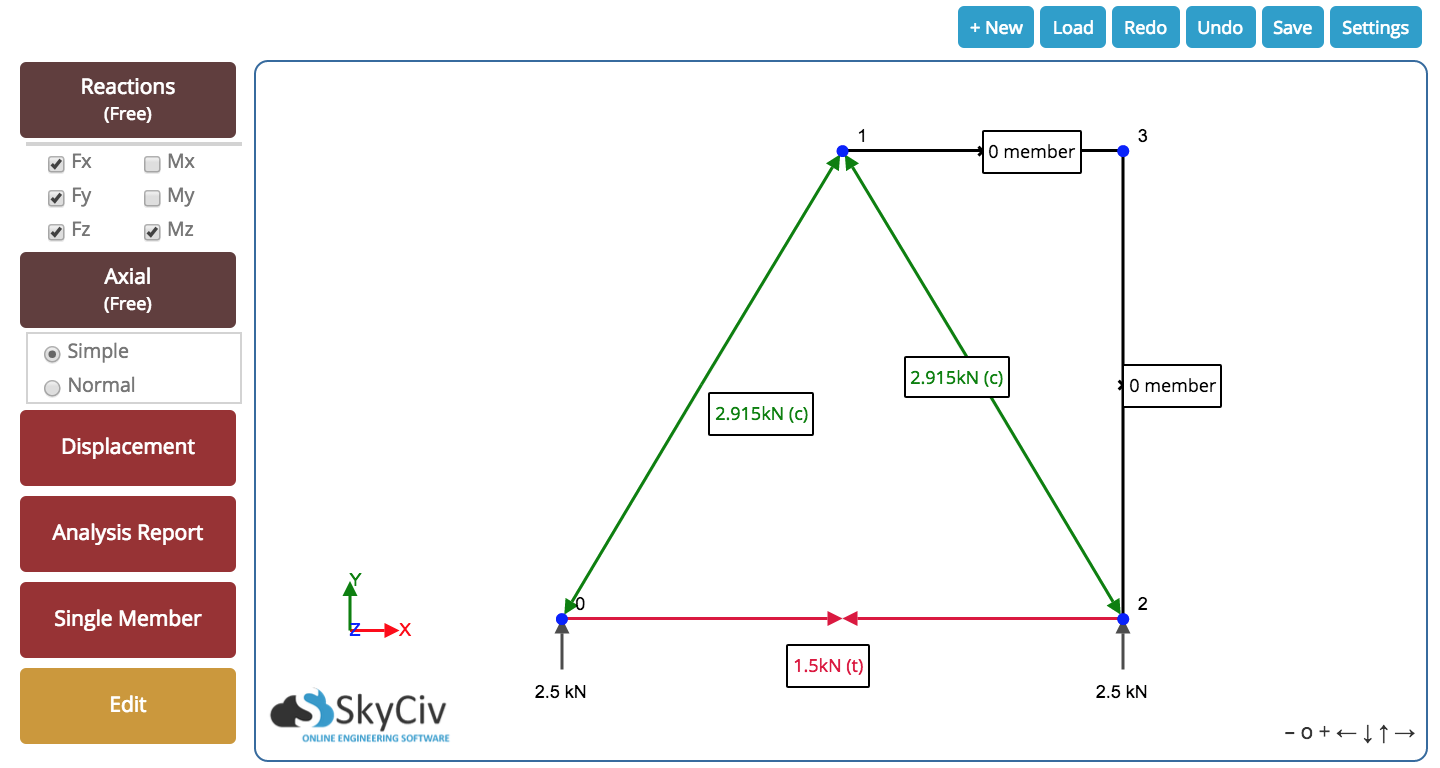
Basit Adımlar
- Her zaman desteklerdeki reaksiyonları hesaplayarak başlayın
- Bilinen bir kuvvete sahip bir nokta seçin ve ona yalıtılmış olarak bakın
- Vektör geometrisini ve kuvvetlerin toplamını kullanın = 0 diğer üye güçleri çözmek için
- Tüm üyeler çözülene kadar işlemi tekrarlayın
- Sıfır Üye'ye dikkat etmeyi unutmayın
İlgili öğretici
- Kafesi kesit yöntemiyle çözme. Bir video ve adım adım kılavuz içerir
SkyCiv Kafes
SkyCiv Kafes Eklem yöntemini sizin için otomatik olarak hesaplayabilir. Veya bizim deneyin Ücretsiz Kafes Hesaplayıcı sana son cevabı verecek olan (elle hesaplama yok).
SkyCiv yazılımının daha fazla işlevselliğini keşfetmek için, başlamak için bugün kaydolun!
