Как рассчитать осевые силы ферменной системы методом соединений?
В этом уроке, мы объясним, как использовать метод соединений для расчета внутренних сил в ферменной системе или конструкции..
Эти силы известны как осевые силы и очень важны при расчете фермы.. Если вам непонятно, что такое ферма, в нашей статье – Что такое ферма. Метод соединений в основном включает рассмотрение каждого из "суставов".’ (где встречаются участники) и применяя статические уравнения для решения.
Самое замечательное в том,, SkyCiv фермы делает это автоматически для вас. Смоделируйте свои собственные фермы, и программа покажет интерактивную пошаговую отработку метода соединений.!
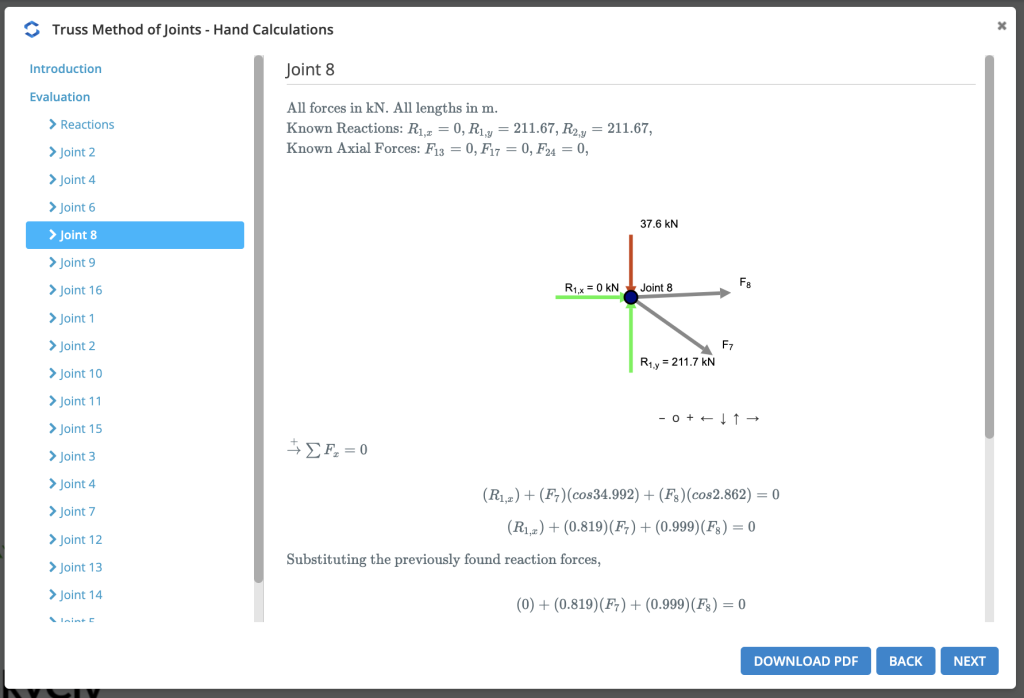
шаг 1: Рассчитайте реакции на опорах.
Первый, мы рассчитываем реакции на опорах. Мы начнем с рассмотрения простого примера 5 стропильная система:
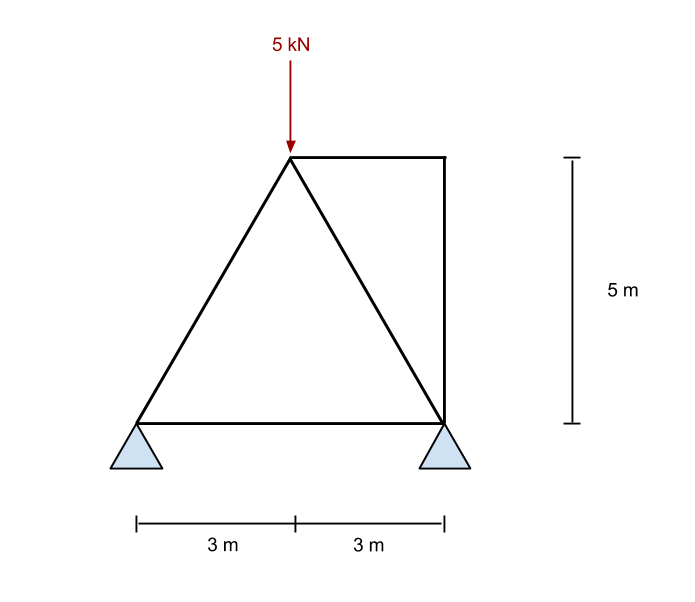
Чтобы рассчитать изгибающий момент в этой стропильной системе, сначала принимаем сумму моментов левой реакции равной нулю. Мы делаем это, игнорируя все элементы и просто глядя на силы и опоры в конструкции.. Это тот же метод, который использовался в реакции на изгибающий момент в нашем предыдущем руководстве..
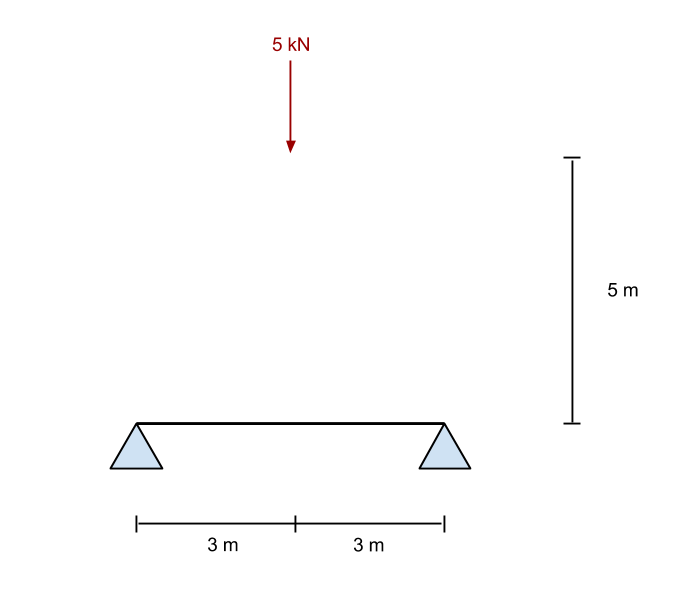
Из приведенных выше уравнений, мы решаем для силы реакции в точке B (правильная поддержка). В нашем примере, это работает, чтобы быть 2.5 кН в направлении вверх. Сейчас же, если мы возьмем сумму сил в y (вертикальный) направление, мы находим, что опора A (левая опора) также дается как 2.5 кН.
шаг 2: Рассмотрим одну из опор:
Теперь, когда у нас есть силы реакции, мы можем приступить к анализу остальной части этой ферменной конструкции.. во-первых, мы смотрим на одну из наших известных сил – в таком случае, рассмотрим левую опорную реакцию +2.5 кН. Поскольку мы знаем, что эта сила возникает в этот момент, мы рассмотрим только этот момент отдельно. Мы повторяем этот процесс несколько раз., поэтому важно попрактиковаться и изучить процесс, чтобы иметь хорошее представление о том, как решать осевые силы в ферменных конструкциях.. Так что еще раз, Рассмотрим первую точку на опоре:
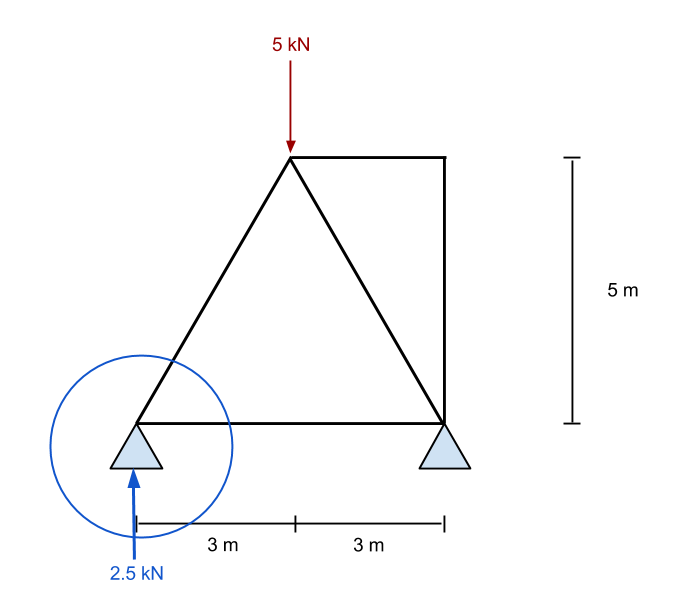
Увеличение этой точки, мы видим все известные силы, действующие на эту точку. Из статики, мы знаем, что силы в направлениях x и y должны в сумме равняться нулю.. Соответственно, если мы знаем, что существует восходящая вертикальная сила, тогда должна быть нисходящая сила, чтобы противодействовать этому. Поскольку у нас уже есть значение силы, направленной вверх, тогда мы попробуем оценить количество участников 1 первый.
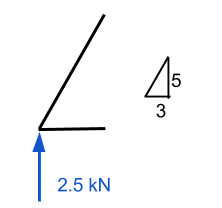
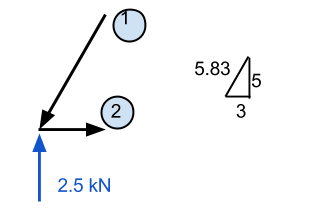
Здесь нам потребуются некоторые знания векторов. Важно помнить, что все силы должны в сумме равняться нулю как для x, так и для y-направлений.. В нашем примере, горизонтальное расстояние 3 м, а вертикальное 5 м – оставляя нас с гипотенузой, приблизительно равной 5.83 м. Используя это, мы можем сделать вывод, что компонент нормальной силы элемента 1 равно (5.83)/(5) умноженное на вертикальную силу 2.5 кН. Это приравнивается к 2.92 кН и ДОЛЖНА быть направленной вниз силой, если точка должна оставаться неподвижной..
Член 2 можно рассчитать примерно так же. Если мы знаем этого члена 1 действует вниз, тогда мы знаем, что он также должен действовать влево. Соответственно, мы знаем члена 2 должен генерировать силу, которая тянет точку вправо, чтобы поддерживать силы в x-направлении. Это значение рассчитывается (3/5.83) Икс 2.92 кН и равно 1.51 кН.
шаг 3: Перейти к другой точке:
Рассчитав внутренние силы первого элемента в нашей ферме, теперь мы посмотрим на другую точку, чтобы повторить процесс:
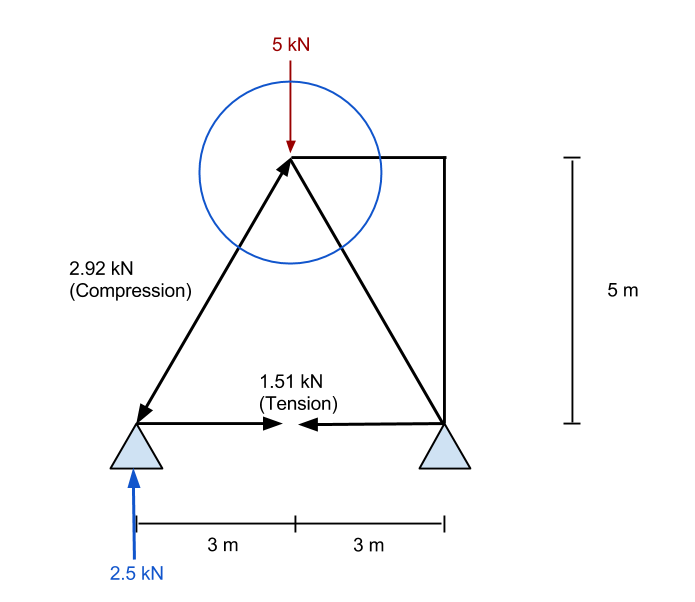
Очередной раз, мы увеличим масштаб до точки отсчета и рассмотрим все известные силы, действующие на точку:
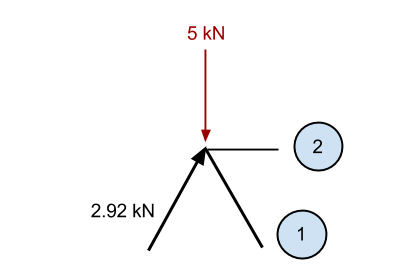
Примерно так же, как и раньше, если суммировать известную вертикальную составляющую 2.92 кН член (2.5 кН в вертикальном направлении) и – 5кН направленная вниз сила, тогда у нас есть избыток в нисходящем направлении 2.5 кН (5 – 2.5). Соответственно, мы знаем этого члена 1 должен вызывать силу в направлении вверх, чтобы острие оставалось неподвижным. Эта сила должна иметь вертикальную составляющую 2.5 кН, и поскольку он находится под тем же углом, что и предыдущий член, тогда внутренняя осевая сила также должна быть 2.92 кН.
Теперь рассмотрим силы в x-направлении. С этой точки зрения, вся вертикальная сила от стержня 1 сопротивляется вертикальной силе предварительно рассчитанного элемента. Это означает, что сумма сил в направлении x уже равна нулю.. Соответственно, не может быть силы в члене 2 иначе точка станет неуравновешенной и перестанет статичной..
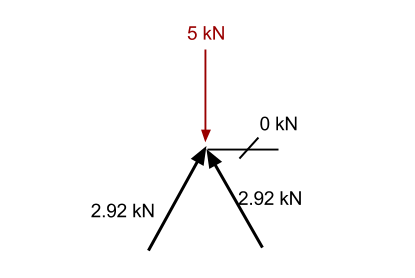
шаг 4: Перейти к другой точке:
Глядя на эту точку, мы видим, что есть особый случай. В этой ситуации, любая сила, отталкивающая вверх, не будет иметь возможного сопротивления, поскольку нет другого элемента, способного обеспечить направленную вниз силу, чтобы удерживать точку в статике. Соответственно, так как сумма сил должна быть равна нулю, этот член не может иметь никакой силы, связанной с ним. Это, следовательно, не имеет силы и известен как нулевой член.
Очередной раз, если мы посмотрим на суммирование сил в x-направлении, мы видим, что есть только один член, который имеет силу в направлении x. Соответственно, это также должно быть 0 осевое усилие, чтобы сумма сил равнялась нулю.
Окончательное решение
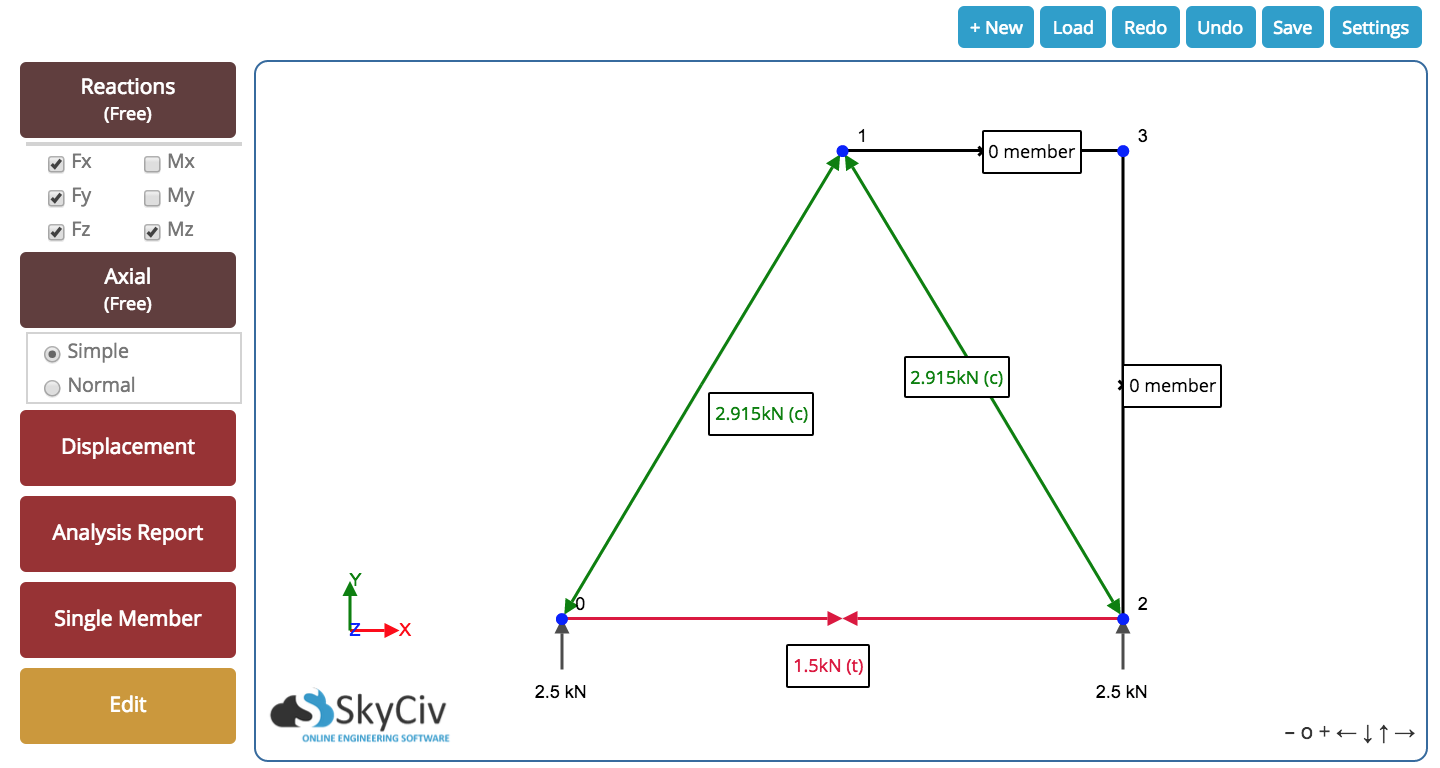
в заключение, мы получаем следующий результат для нашей фермы. Мы можем видеть все результирующие осевые силы внутри элемента и реакции на опорах. Следующий результат был взят из нашего Бесплатный калькулятор фермы – Попробуй, это бесплатно!
Простые шаги
- Всегда начинайте с расчета реакции на опоры
- Выберите точку с известной силой и посмотрите на нее изолированно.
- Используйте векторную геометрию и сумму сил = 0 решить другие члены сил
- Повторяйте процесс, пока все члены не будут решены.
- Не забывайте остерегаться нулевых участников
Соответствующий учебник
- Решение фермы методом сечений. Включает видео и пошаговое руководство
SkyCiv фермы
SkyCiv фермы может рассчитать метод суставов автоматически для вас. Или попробуйте наш Бесплатный калькулятор фермы который даст вам окончательный ответ (без ручных расчетов).
Чтобы изучить больше функциональных возможностей программного обеспечения SkyCiv, зарегистрируйтесь сегодня, чтобы начать!
