Основы момента инерции

Момент инерции может быть получен как получение момент инерции частей и применяя формулу переноса: Я = Я₀ + Объявление². У нас есть обширная статья, объясняющая подход к решить момент инерции.

В корне, момент инерции - второй момент площади, что можно выразить следующим образом::

[математический] Я_{Икс}= int int y ^{2}дает [математический] [математический] Я_{и}= int int х ^{2}дает [математический]

Чтобы увидеть вывод формул ниже, мы пытаемся найти момент инерции объекта, такого как прямоугольник, вокруг его большой оси, используя формулу выше. Чтобы получить момент инерции, пределы должны быть определены таким образом, чтобы они проводились от оси вращения до ее крайнего волокна.. Это были бы пределы внешнего интеграла. Внутренний интеграл имеет предел от 0 к б. Это сказал, мы также можем выразить dA как xdy, который станет bdy. Поскольку ось вращения находится на нейтральной оси, момент инерции можно интегрировать с верхним пределом h / 2 и нижним пределом 0 и умноженный вдвое за счет симметрии прямоугольника. Это оставляет нам интеграл ниже.

[математический] Я_{Икс}= 2 int_{0}^{\гидроразрыва{час}{2}} и ^{2}бди [математический] Интеграция, [математический] Я_{Икс}= 2b left [ \гидроразрыва{и ^{3}}{3} \право ]_{0}^{\гидроразрыва{час}{2}} [математический] [математический] Я_{Икс}= 2b left [ \гидроразрыва{ч ^{3}}{24}-0 \право ] [математический] [математический] Я_{Икс}= Гидроразрыва{бх ^{3}}{12} [математический]

Формула момента инерции для сечений балки

SkyCiv составил сводку уравнений момента инерции для секций балки. (второй момент площади). Уравнения момента инерции чрезвычайно полезны для быстрых и точных расчетов.. Для вашего удобства формулы сведены в простейшие формы..

SkyCiv также предлагает Калькулятор свободного момента инерции для быстрых расчетов или проверки правильности применения формулы. Формула момента инерции прямоугольника, круг, даны полые и треугольные сечения балок. Некоторые важные вещи, которые следует помнить о моменте инерции площади балки::

• Момент инерции площади отличается от момента инерции массы.
• Он также известен как второй момент площади.
• Это значительный фактор прогиба (чем больше я_Икс, нижний прогиб будет)
• Единицы имеют длину в степени 4
• Приведенные ниже уравнения дают момент инерции относительно центра тяжести сечения.

ССЫЛКА	яхх	ягг
Уравнение момента инерции для прямоугольного или прямоугольного сечения
	[математический] \dfrac{бх ^ 3}{12} [математический]	[математический] \dfrac{Ь ^{3}час}{12} [математический]
Уравнение момента инерции полого прямоугольного сечения.
	[математический] \dfrac{бх ^ 3}{12} – \dfrac{b_1h_1 ^ 3}{12} [математический]	[математический] \dfrac{b ^ 3h}{12} – \dfrac{b_1 ^ 3h_1}{12} [математический]
Уравнение момента инерции для окружности или кругового сечения
	[математический] \dfrac{\число Пи}{64}D ^ 4 [математический]	[математический] \dfrac{\число Пи}{64}D ^ 4 [математический]
Уравнение момента инерции для полого кругового сечения.
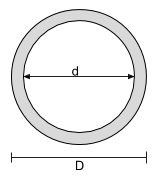	[математический] \dfrac{\число Пи}{64}D ^ 4 – \dfrac{\число Пи}{64}d ^ 4 [математический]	[математический] \dfrac{\число Пи}{64}D ^ 4 – \dfrac{\число Пи}{64}d ^ 4 [математический]
Уравнение момента инерции для равнобедренного треугольника.
	[математический] \dfrac{бх ^ 3}{36} [математический]	[математический] \dfrac{3b ^ 3h}{144} [математический]
Уравнение момента инерции двутавра.
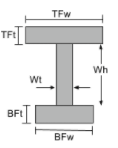	[математический] \гидроразрыва{TFw раз TFt ^{3}}{12} +\гидроразрыва{Wt раз Wh ^{3}}{12} + \гидроразрыва{BFw раз BFt ^{3}}{12} +[математический] [математический] TFw times TFt times left ( BFT + Wh + frac{Tft}{2} -\бар{и}_{бот} \право )^{2} +[математический] [математический] Wt times Wh times left ( BFt + frac{белый}{2} -\бар{и}_{бот} \право )^{2} +[математический] [математический] BFw times BFt times left ( \гидроразрыва{белый}{2} -\бар{и}_{бот} \право )^{2} [математический]	[математический] \гидроразрыва{TFt раз TFw ^{3}}{12} + \гидроразрыва{Wh times Wt ^{3}}{12} + \гидроразрыва{BFt раз BFw ^{3}}{12} [математический]
Уравнение момента инерции таврового сечения
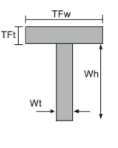	[математический] \гидроразрыва{TFw раз TFt ^{3}}{12} + \гидроразрыва{Wt раз Wh ^{3}}{12} +[математический] [математический] TFw times TFt left ( белый + \гидроразрыва{Tft}{2} -\бар{и}_{бот} \право )^{2} +[математический] [математический] Wt times Wh times left ( \гидроразрыва{белый}{2} – \бар{и}_{бот} \право )^{2} [математический]	[математический] \гидроразрыва{TFt раз TFw ^{3}}{12} + \гидроразрыва{Wh times Wt ^{3}}{12} [математический]
Уравнение момента инерции участка канала.
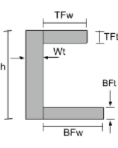	[математический] \гидроразрыва{TFw раз TFt ^{3}}{12} + \гидроразрыва{BFw раз BFt ^{3}}{12} + \гидроразрыва{Wt раз h ^{3}}{12} +[математический] [математический] TFw times TFt times left ( час – \гидроразрыва{Tft}{2} – \бар{и}_{бот} \право )^{2} +[математический] [математический] BFw times BFt times left ( \гидроразрыва{BFT}{2} – \бар{и}_{бот} \право )^{2} +[математический] [математический] Wt times h times left ( \гидроразрыва{час}{2} – \бар{и}_{бот} \право )^{2} [математический]	[математический] \гидроразрыва{TFt раз TFw ^{3}}{12} + \гидроразрыва{BFt раз BFw ^{3}}{12} + \гидроразрыва{h раз Wt ^{3}}{12} +[математический] [математический] TFt times TFw times left ( вес + \гидроразрыва{TFW}{2} – \бар{Икс}_{осталось} \право )^{2} +[математический] [математический] BFt times BFw times left ( вес + \гидроразрыва{BFW}{2} – \бар{Икс}_{осталось} \право )^{2} +[математический] [математический] h times Wt times left ( \гидроразрыва{вес}{2} – \бар{Икс}_{осталось} \право )^{2} [математический]
Момент инерции Уравнение углов
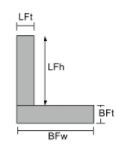	[математический] \гидроразрыва{BFw раз BFt ^{3}}{12} + \гидроразрыва{ LFt раз LFh ^{3}}{12} +[математический] [математический] BFw times BFt times left ( \гидроразрыва{BFT}{2}-\бар{и}_{бот} \право )^{2} +[математический] [математический] LFt times LFh times left ( BFT + \гидроразрыва{LFH}{2}-\бар{и}_{бот} \право )^{2} [математический]	[математический] \гидроразрыва{BFt раз BFw ^{3}}{12} + \гидроразрыва{ LFh раз LFt ^{3}}{12} +[математический] [математический] BFt times BFw times left ( \гидроразрыва{BFW}{2}-\бар{Икс}_{осталось} \право )^{2} +[математический] [математический] LFh times LFt times left ( \гидроразрыва{LFt}{2}-\бар{Икс}_{осталось} \право )^{2} [математический]

Используйте SkyCiv Section Builder для ручных расчетов

В этой статье, мы провели вас через формулу момента инерции. Для получения дополнительной информации по этой теме, посетите наш урок на Момент инерции сечения балки.

Вы знали SkyCiv Раздел Строитель также показывает полные расчеты для следующих форм?

• прямоугольный, Полый прямоугольный
• круговое, Полый круговой
• I-Beam, Тавровая балка
• Угол (L-луч), канал
• Треугольные секции

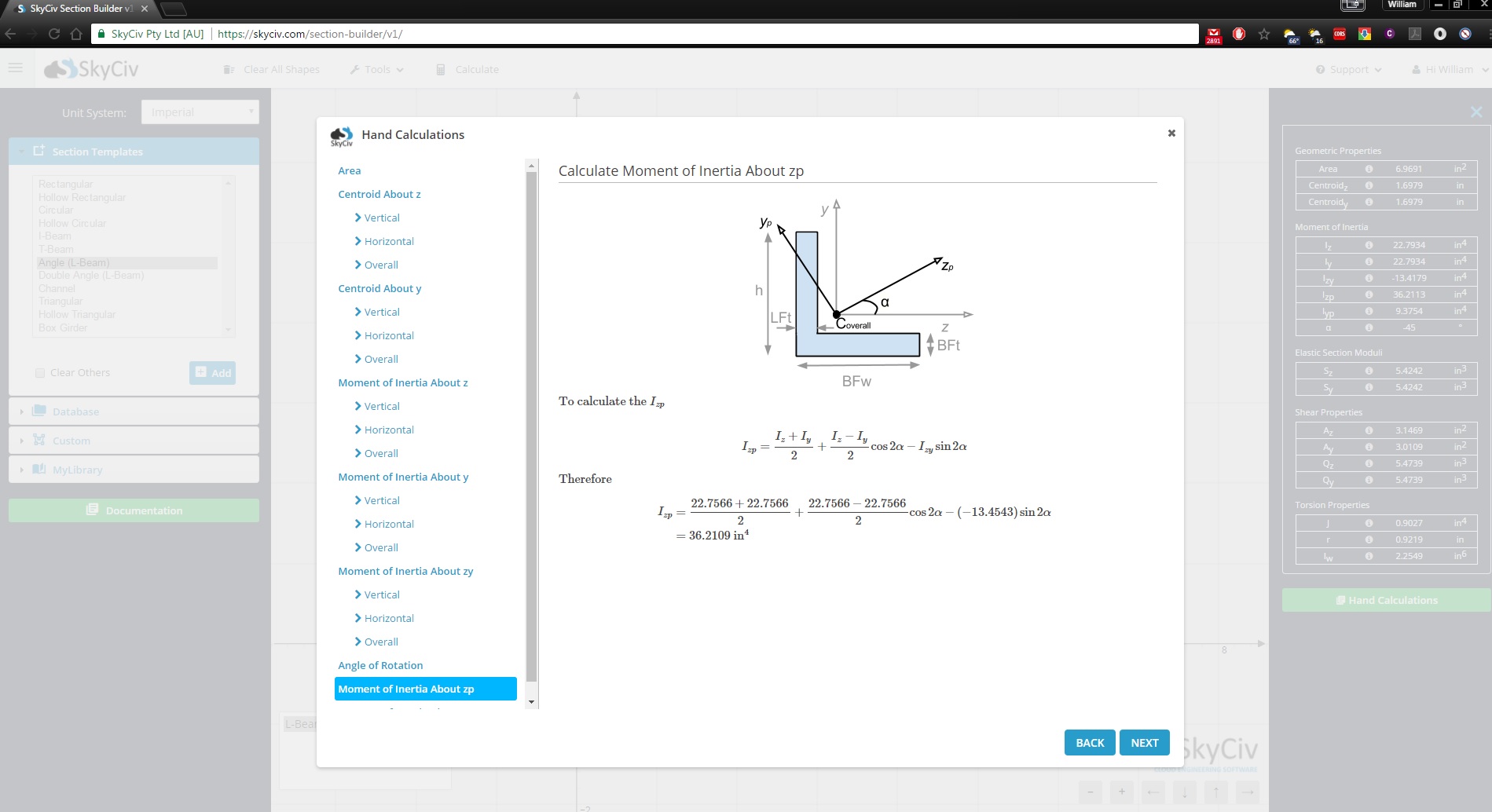
Мы надеемся, что приведенная выше таблица окажется полезной для расчета момента инерции окружности., треугольник, и момент инерции прямоугольника среди других форм. Также у нас есть полезный Калькулятор момента инерции, упрощенный из SkyCiv Раздел Строитель, который обрабатывает эти расчеты для вас, или зарегистрируйтесь сегодня, чтобы начать работу с программным обеспечением SkyCiv!