При запуске Анализ спектра реакции на структуре, одним из наиболее важных шагов для получения желаемых результатов является определение метода комбинирования мод, который будет использоваться программным обеспечением для получения единого результата для смещения., реакции, внутренние силы, и т.д… для каждой степени свободы из необработанных результатов, полученных для каждой формы колебаний (модальные ответы). Эти модальные комбинированные результаты используются для проектирования структуры., Вот почему правильное определение метода модальной комбинации чрезвычайно важно. В этой статье, мы углубимся в некоторые модальные комбинированные методы анализа спектра отклика..
Важно отметить, что одним из наиболее важных этапов анализа спектра отклика является оценка собственной частоты для каждой формы вибрации и ее массового вклада., ознакомьтесь с нашей документацией по динамическому частотному анализу.
Методы модальной комбинации для анализа спектра отклика
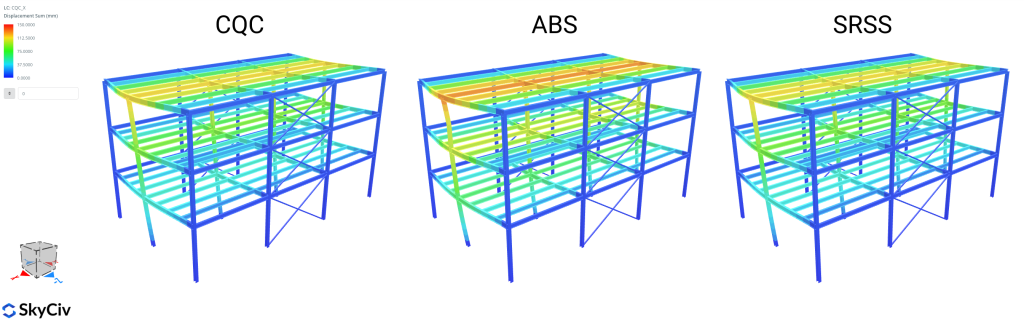
Некоторые из наиболее известных и используемых методов модального сочетания::
- АБС: Абсолютная сумма
- SRSS: Квадратный корень из суммы квадратов
- CQC: Полная квадратичная комбинация
В общем, пиковые значения общего отклика (\(r_o\)) для перемещений, внутренние силы, и реакции интересны. Как упоминалось ранее, это пиковое значение получается при правильном объединении пиковых модальных откликов (\(р_{N, О}\))
Абсолютная сумма (АБС)
Метод модальной комбинации Absolute Sum принимает абсолютное значение результата (перемещение или внутренняя сила) для каждого режима вибрации и суммирует все эти абсолютные значения. Физически, предполагается, что все пиковые модальные реакции возникают одновременно. Делая это, это самый консервативный метод, так как это делает каждый модальный вклад положительным, и поэтому, он не популярен в приложениях для проектирования конструкций. Формула для расчета пикового значения общего отклика::
\(r_o=\sum_{п=1}^{N} |р_{N,О}|\)
куда,
\(n\) это \(п^{th}\) режим вибрации, учитываемый при анализе
\(Н) - общее количество форм вибрации, рассматриваемых при анализе
\(r_o\) пиковый общий ответ
\(р_{N,О}\) пиковый модальный отклик для \(п^{th}\) режим вибрации
Квадратный корень из суммы квадратов (SRSS)
Метод модального комбинирования квадратного корня из суммы квадратов извлекает квадратный корень из суммы квадратов результата для каждого режима вибрации., предоставление оценки пика общего ответа. Этот метод комбинирования мод обеспечивает отличные оценки отклика для структур с хорошо разделенными собственными частотами., в случаях, когда собственные частоты конструкции плохо разделены, этот метод не следует использовать.. Формально, пиковый общий ответ может быть выражен следующим образом:
\(r_o=\left(\сумма_{п=1}^{N} г ^{2}_{N,О}\право)^{1/2}\)
куда,
\(n\) это \(п^{th}\) режим вибрации, учитываемый при анализе
\(Н) - общее количество форм вибрации, рассматриваемых при анализе
\(r_o\) пиковый общий ответ
\(р_{N,О}\) пиковый модальный отклик для \(п^{th}\) режим вибрации
Полная квадратичная комбинация (CQC)
Метод полного квадратичного комбинирования преодолевает ограничение, упомянутое для SRSS, при комбинировании модальных откликов в конструкции с близко расположенными собственными частотами.. По Мейергофу, пиковый общий отклик получают, применяя следующую формулу:
\(r_o=\left(\сумма_{я = 1}^{N}\сумма_{п=1}^{N} \расстояние от центра колонны{в} \cdot r_{ио} \cdot r_{нет} \право)^{1/2}\)
куда,
\(N, \; i\) это \(п^{th}, \; я ^{th}\) режим вибрации, учитываемый при анализе
\(Н) - общее количество форм вибрации, рассматриваемых при анализе
\(r_o\) пиковый общий ответ
\(р_{N,О}, \; р_{я,О}\) пиковый модальный отклик для \(п^{th}, \; я ^{th}\) режим вибрации
\(\расстояние от центра колонны{в}\) - коэффициент корреляции для двух мод, объединяемых на каждом шаге суммирования
Приведенную выше формулу можно переписать в виде двух отдельных групп сумм., первый идентичен методу модального комбинирования SRSS.. Второе двойное суммирование включает в себя все перекрестные (\(i \neq n\)) термины, каждый из которых может быть положительным или отрицательным, это приводит к тому факту, что оценка пикового общего ответа с использованием CQC может быть больше или меньше, чем оценка, предоставленная SRSS. :
\(r_o=\left( \сумма_{п=1}^{N} г ^{2}_{N,О} + \подкос{\сумма_{я = 1}^{N}\сумма_{п=1}^{N}}_{i \neq n} \расстояние от центра колонны{в} \cdot r_{ио} \cdot r_{нет} \право)^{1/2}\)
Только один член в уравнении для CQC не определен: коэффициент корреляции. Одним из наиболее часто используемых уравнений для этого коэффициента является:
\(\расстояние от центра колонны{в} = frac{\xi^2(1+\бета_{в})^ 2}{(1-\бета_{в})^2+4\xi^2\beta_{в}}\)
куда,
\(\бета_{в}\) отношение собственных частот \(я ^{th}\) и \(п^{th}\) режимы (\(\омега_и / \omega_n\))
\(\xi) - коэффициент демпфирования конструкции
Ссылки
Чопра, А. (2015, июнь 4). Динамика структур (4изд.). Пирсон Высшее образование.
Новое в SkyCiv Structural 3D? Зарегистрируйтесь сегодня бесплатно!
Разработчик продукта
BEng (гражданского)



