Момент инерции - важное геометрическое свойство, используемое в строительстве.. Это напрямую связано с количеством прочности материала, которое имеет ваша секция.. В общем-то, более высокий момент инерции подразумевает большую прочность в сечении, что приводит к уменьшению прогиба при воздействии нагрузки. Обозначение “момент инерции” на самом деле это широко распространенное неправильное название, поскольку это свойство не имеет ничего общего с инерцией. На самом деле правильное техническое название Второй момент площади. Это обозначение более точно описывает, в чем измеряется данное свойство., что можно грубо оценить как меру того, насколько далеко площадь сечения находится от нейтральной оси..

Оглавление

• Момент инерции формулы прямоугольника
• Прямоугольные полые секции (RHS)

Момент инерции формулы прямоугольника

Общая формула, используемая для определения момента инерции прямоугольника::

[математический] Я_{хх}=dfrac{БД^3}{12} , Я_{гг}=dfrac{Б^3D}{12} [математический]

Где хх и гг относятся к конкретной оси, или направление, рассматривается.

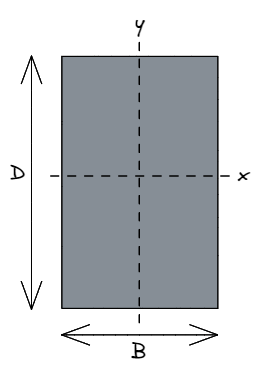
Это общепринятое соглашение по проектированию конструкций, согласно которому В относится к ширина прямоугольника, параллельно с обычным горизонтальный ось x.

так же, D относится к глубина прямоугольника, параллельно с обычным вертикальный ось Y.

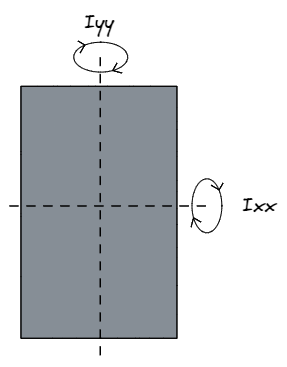
Когда инженеры-строители обращаются к икс они ссылаются на силу раздела о ось абсцисс, то есть в направлении, параллельном D измерение, или ось Y. так же, ГГГ относится к силе о ось Y, то есть в направлении, параллельном В измерение, или ось x.

Прямоугольные полые секции (RHS)

В то время как инженеры могли гипотетически использовать сплошные прямоугольные сечения при проектировании, это потребует значительно большего количества сырья, с соответствующим увеличением веса и стоимости. Гораздо чаще используют прямоугольные полые секции (обычно называют RHS). Здесь мы можем использовать то же уравнение, определенное выше для общего прямоугольного случая., тем не мение, мы должны вычесть внутреннюю пустой площадь прямоугольника:

[математический] Я_{хх}=dfrac{БД^3}{12} – \dfrac{бд^3}{12} [математический]

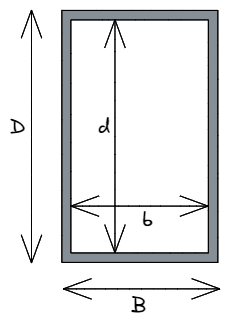
В этом случае, нижний регистр б и d обозначают размер полой области внутри прямоугольника, который мы должны вычесть из внешних размеров фигуры, в верхнем регистре В и D. Разница между каждым соответствующим размером относится к толщине материала в этом измерении. – т.е.. В – b = общая толщина материала параллельно оси x.

Помимо наглядных примеров использования веса и материала, почему полые секции часто описываются как более эффективный чем их солидные собратья?

Рассмотрим балку, испытывающую вертикальную нагрузку вниз. Мы ожидаем, что самые верхние волокна материала будут подвергаться сжимающей силе., при этом соответствующие нижние волокна будут подвергаться растягивающей силе. Волокна вдоль нейтральной оси сечения (параллельно центроиду сечения) тем не мение, не будет испытывать ни сжатия, ни растяжения, отсюда и название нейтральный ось.

Важно, в величина этих сил сжатия или растяжения зависят от расстояния от этой нейтральной оси – материал ближе к нейтральной оси должен сопротивляться меньше сила.

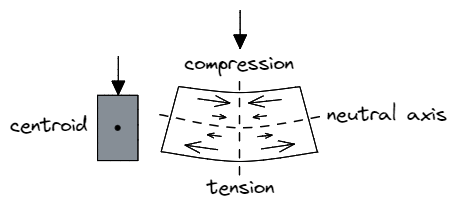
В следствии, внутренний материал цельной секции сопротивляется лишь небольшой силе, занимая при этом большую площадь, поскольку самый внешний материал несет наибольшую нагрузку! Удаление этой внутренней части секции и создание ее полой, следовательно, улучшает эффективность сечения в зависимости от его веса, Стоимость, и использование материалов.

Вывод

В итоге, формула для определения момента инерции прямоугольника Ixx=BD³ ⁄ 12, Iyy=B³D ⁄ 12. Для прямоугольных полых профилей, формула Ixx=BD³ ⁄ 12 – бд³ ⁄ 12.

Момент инерции важен как для силы/напряжения изгибающего момента, так и для прогиба.. Это видно по их формулам., как в обоих случаях, я (Момент инерции) находится в знаменателе:

Источник: используя формулу

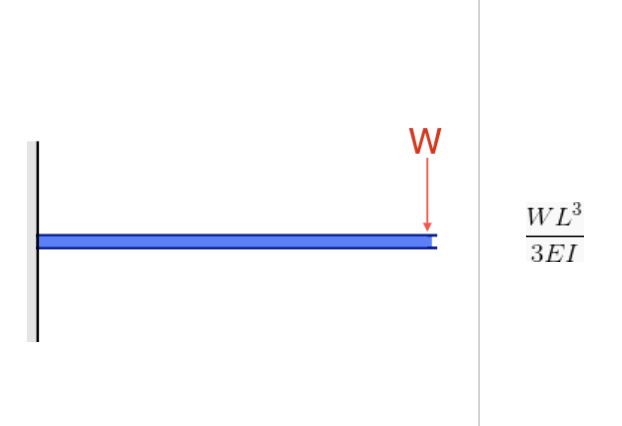
Источник: Уравнение прогиба в консольной балке

Калькулятор момента инерции окружности

Если вы хотите узнать больше, ознакомьтесь с нашим учебным пособием по Момент инерции круга чтобы увидеть, как сравниваются формы круглого и прямоугольного сечения.

Калькулятор свободного момента инерции