Оглавление

• Расчет диаграммы изгибающего момента
• и может быть адаптирован к различным типам задач
• Правила знаков для диаграмм изгибающих моментов
• Как рассчитать изгиб с помощью балки SkyCiv

Расчет диаграммы изгибающего момента

Ниже приведены простые инструкции о том, как рассчитать диаграмму изгибающего момента балка с простой опорой. Изучите этот метод, так как он очень универсален. (и может быть адаптирован к различным типам задач. Возможность рассчитать момент луч это очень распространенная практика для инженеров-строителей и часто встречается на экзаменах в колледже и средней школе.. Полезно заранее заметить, что программное обеспечение SkyCiv Beam может отображать эти ручные расчеты мгновенно и автоматически! Мы будем следовать сегодняшнему руководству с примером, взятым непосредственно из модуля расчета рук в SkyCiv Beam..

во-первых, что такое изгибающий моментT? Момент - это вращательная сила, которая возникает, когда сила прикладывается перпендикулярно к точке на заданном расстоянии от этой точки.. Он рассчитывается как перпендикулярная сила, умноженная на расстояние от точки. Изгибающий момент - это просто изгиб, возникающий в балке из-за момента.

При расчете изгибающих моментов важно помнить две вещи.; (1) стандартные единицы - Нм и (2) при сдавливании верхнего волокна, изгиб считается положительным. С определениями в сторону, давайте посмотрим, как рассчитать диаграмму изгибающего момента!

Бесплатный Калькулятор Луча

и может быть адаптирован к различным типам задач

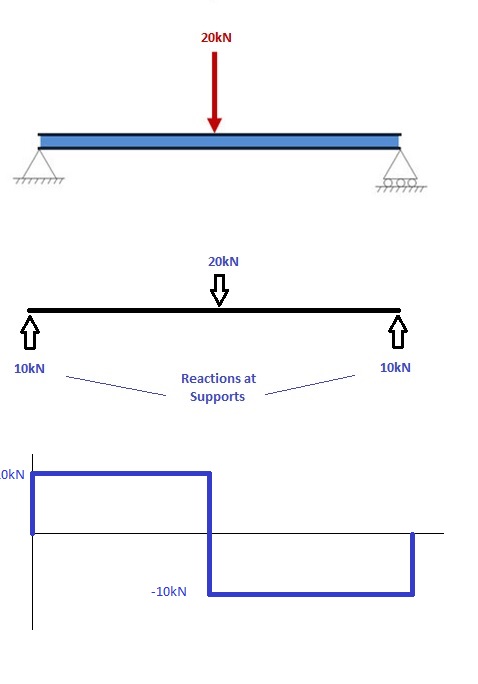
1. Рассчитайте реакции на опорах и начертите диаграмму свободного тела. (FBD)

Если вы не знаете, как определить реакции на опорах – пожалуйста, сначала посмотрите это руководство. Как только у вас будет реакция, нарисуйте диаграмму свободного тела и Диаграмма усилия сдвига под балкой. Окончательно вычислить моменты можно, выполнив следующие действия.:

2. Слева направо, делать “порезы” до и после каждой реакции / нагрузки

Для расчета изгибающего момента балки, мы должны работать так же, как мы делали для диаграммы силы сдвига. Начиная с x = 0 будем перемещаться по балке и вычислять изгибающий момент в каждой точке.

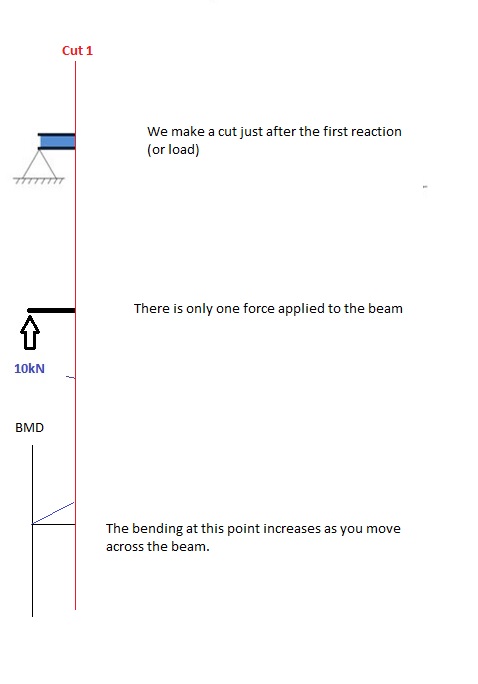
Резать 1

Сделать “резать” сразу после первой реакции луча. В нашем простом примере:

Так, когда мы разрезаем луч, мы учитываем только силы, приложенные слева от нашего разреза. В таком случае, у нас есть сила 10 кН в направлении вверх. Теперь, как вы помните, изгибающий момент - это просто сила x расстояние. Так что по мере того, как мы удаляемся от силы, величина изгибающего момента увеличится. Мы видим это в нашей БМД.. Уравнение для этой части нашей диаграммы изгибающего момента::

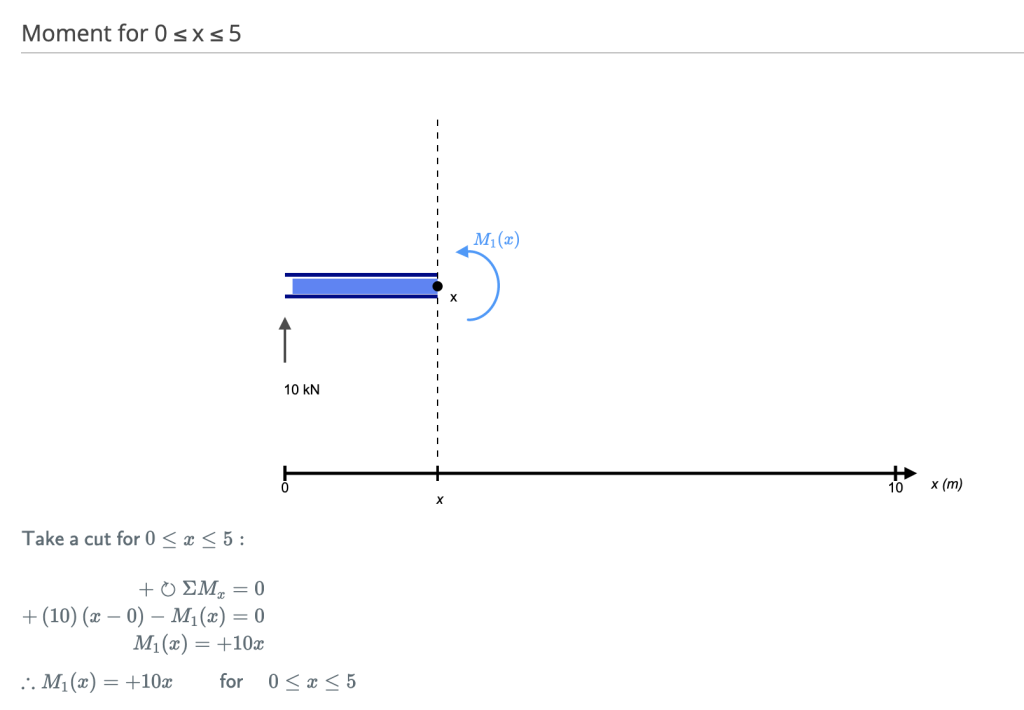
[Источник: SkyCiv Модуль расчета руки луча]

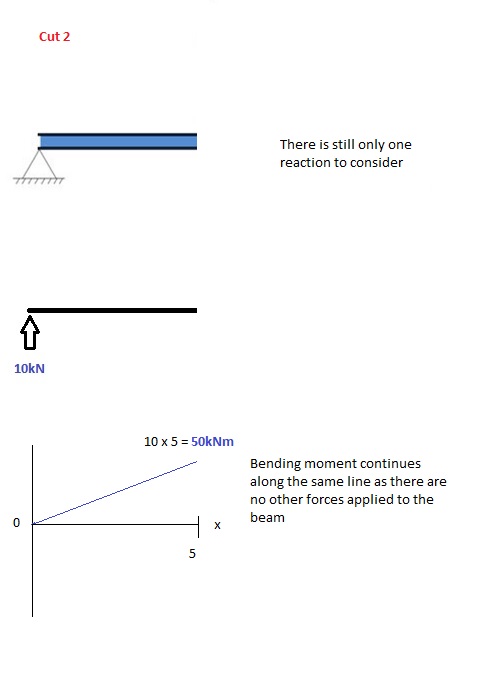
Резать 2

Этот разрез делается непосредственно перед второй силой по балке.. Поскольку между первым и вторым резом нет других нагрузок, в уравнение изгибающего момента останется прежним. Это означает, что мы можем рассчитать максимальный изгибающий момент. (в этом случае в середине, или x = 5) просто подставив x = 5 в приведенное выше уравнение:

Резать 3

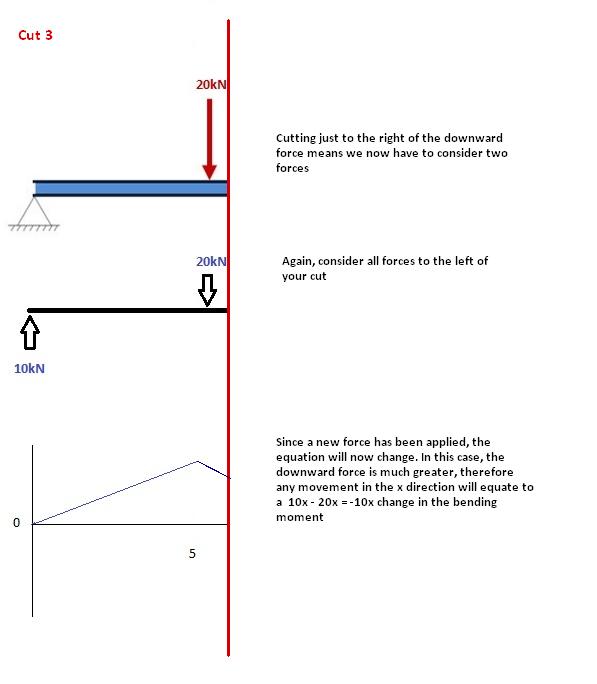
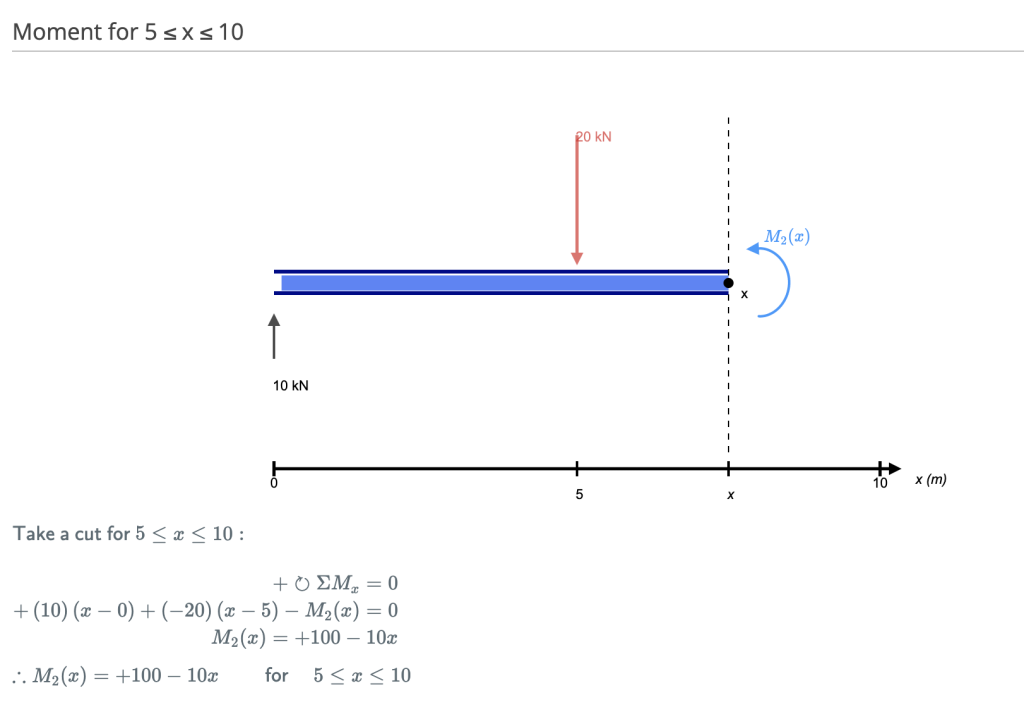
Этот разрез делается сразу после второй силы по балке.. Теперь у нас есть ДВЕ силы, которые действуют слева от нашего разреза.: реакция опоры 10 кН и нагрузка -20 кН, действующая вниз. Итак, теперь мы должны учитывать обе эти силы по мере продвижения по нашей балке.. На каждый метр мы перемещаемся по балке, будет добавлен момент +10 кНм от первого усилия и -20 кНм от второго.

Итак, после точки x = 5, наше уравнение изгибающего момента становится: M(Икс) знак равно 50 +10(х-5) – 20(х-5) M(Икс) знак равно 50 -10(х-5) для 5 ≤ х ≤ 10 ПРИМЕЧАНИЕ: Причина, по которой мы пишем (х-5) потому что мы хотим знать расстояние от точки x = 5 только. Все, что до этой точки, использует предыдущее уравнение.[Источник: SkyCiv Модуль расчета руки луча]

Резать 4

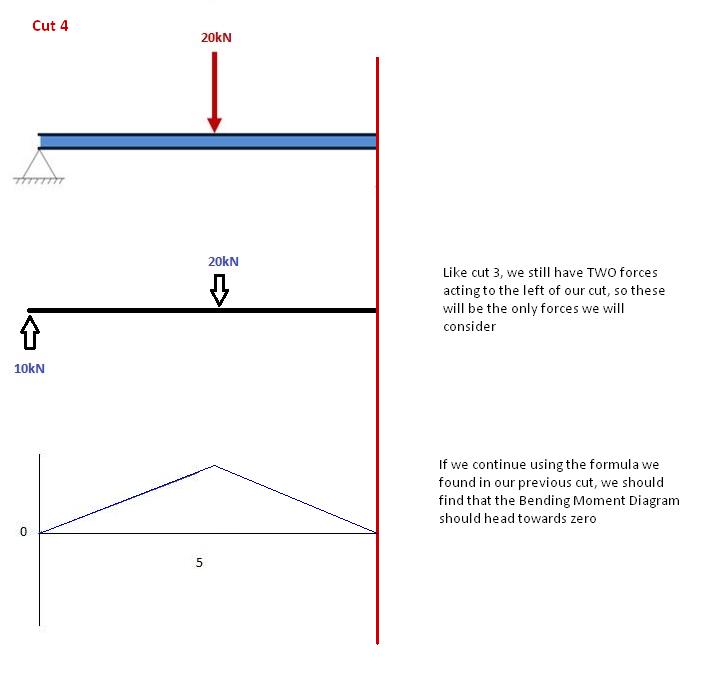
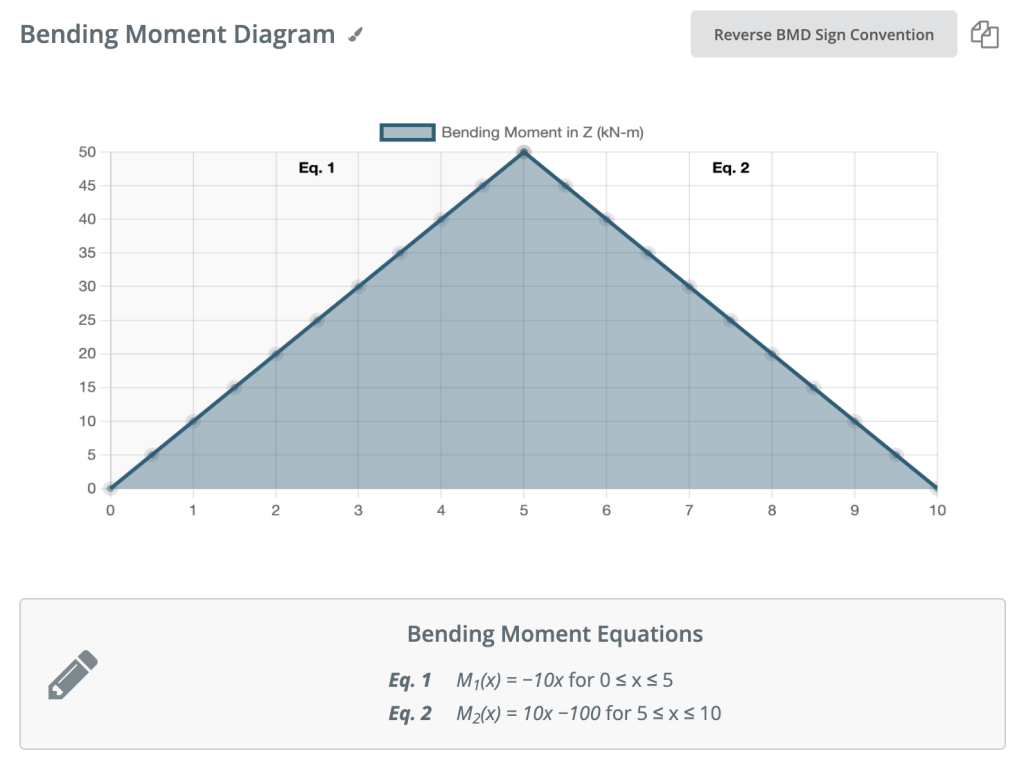
Очередной раз, давайте переместимся вправо от нашей балки и сделаем разрез прямо перед нашей следующей силой. В таком случае, наше следующее сокращение произойдет незадолго до реакции со стороны Right Support. Поскольку между опорой и нашим предыдущим разрезом нет других сил, уравнение останется прежним: M(Икс) знак равно 50 -10(х-5) для 5 ≤ x≤ 10 И давайте подставим в это значение x = 10, чтобы найти изгибающий момент на конце балки.: M(Икс) знак равно 50 – 10(10-5) = 0кНм Это имеет смысл. Поскольку наш луч статичен (и без вращения) Имеет смысл, что наша балка должна иметь нулевой момент в этот момент, если учесть все наши силы. Он также удовлетворяет одному из наших начальных условий, что сумма моментов на опоре равна нулю. ПРИМЕЧАНИЕ: Если ваши расчеты приводят вас к любому другому числу, кроме 0, ты сделал ошибку!

Окончательный результат, как показано в SkyCiv Beam:

Правила знаков для диаграмм изгибающих моментов

О том, как найти изгибающий момент, мы говорили выше.. Диаграммы изгибающих моментов могут несколько запутать, когда дело доходит до соглашений о знаках.. Вы можете увидеть одну и ту же диаграмму, нарисованную в противоположных направлениях в зависимости от источника.. Соглашение о знаках, используемое SkyCiv, показано ниже..

Положительный изгибающий момент:

Если изгибающий момент положителен, верхнее волокно балки сжато.

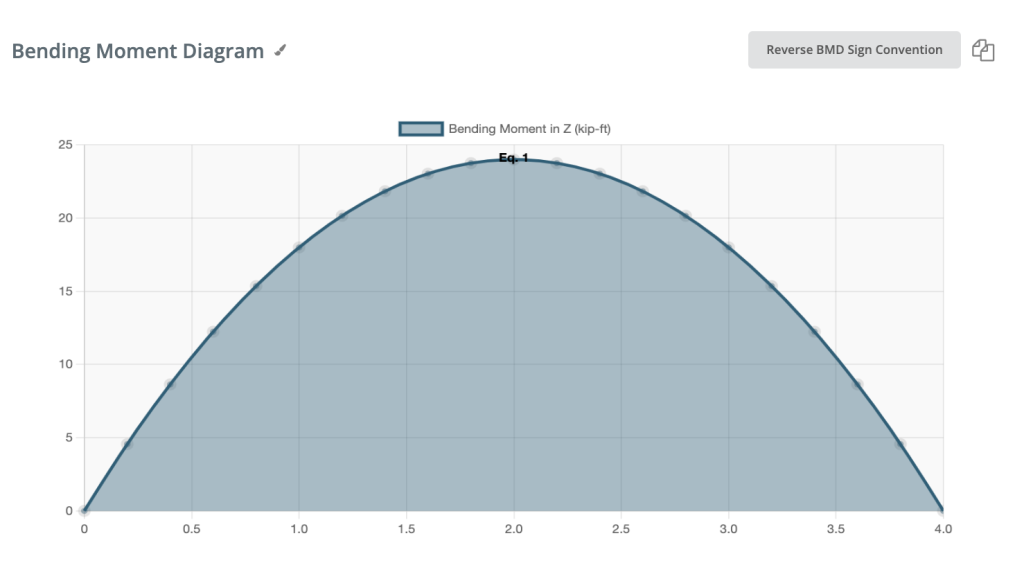
Отрицательный изгибающий момент:

Если изгибающий момент отрицательный, нижнее волокно балки сжато.

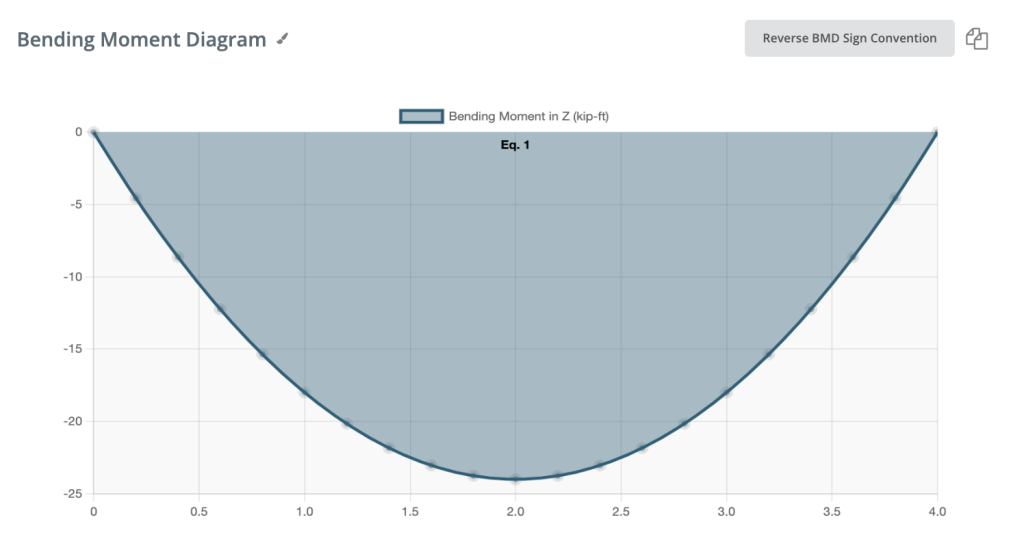
Это было руководство по расчету диаграмм изгибающих моментов., если вы хотите узнать больше по этой теме, посетите наш Beam Tutorials страница. Здесь вы можете найти много других полезных руководств, таких как формула напряжения изгиба или определить реакции на опорах.

БОНУС: Найдите изгибающий момент с помощью SkyCiv Beam

В рамках нашей платной версии SkyCiv Beam Калькулятор покажет вам полные ручные расчеты и шаги, предпринятые для ручного расчета диаграмм изгибающих моментов.. Просто смоделируйте балку с помощью калькулятора, и нажмите решить. Он покажет вам пошаговые расчеты того, как нарисовать диаграмму изгибающего момента. (включая порезы).