Общее описание
SkyCiv имеет надежный и усовершенствованный модуль для проектирования железобетонных плит.. Чтобы получить доступ к этой функции, вы должны сначала построить модель в SkyCiv S3D, а затем вызвать модуль для автоматического расчета с различными строительными кодами, такими как ACI-318., европейским и австралийским стандартам, и так далее. Основная цель модуля при проектировании пластин — указать количество арматурных стержней вдоль пластины..
фигура 1. Модуль проектирования плит SkyCiv
Если вы новичок в SkyCiv, Зарегистрируйтесь и протестируйте программу самостоятельно!
Документация SkyCiv предоставляет отличный контент., включая примеры и случаи анализа, как для изучения, если вы новичок в модулях, так и для сравнения результатов модуля проектирования пластин с ручными расчетами. Не стесняйтесь проверить наши примеры дизайна в соответствии с АКИ-318, Еврокод, и AS3600.
Мы предлагаем вам прочитать эту статью, прежде чем глубоко анализировать сложные системы перекрытий.. Вот, вы узнаете, как изменяются изгибающие моменты в зависимости от размеров плиты в плане. Есть два случая обучения, односторонние и двусторонние плиты. Так, давайте начнем читать!
Одностороннее и двустороннее поведение плиты
Давайте рассмотрим пример плиты на следующем изображении., где есть опора на каждом крае плиты, и мы устанавливаем, что это будет вести себя как двусторонняя пластина, то есть, имеющий изгибающий момент в двух основных направлениях плана.
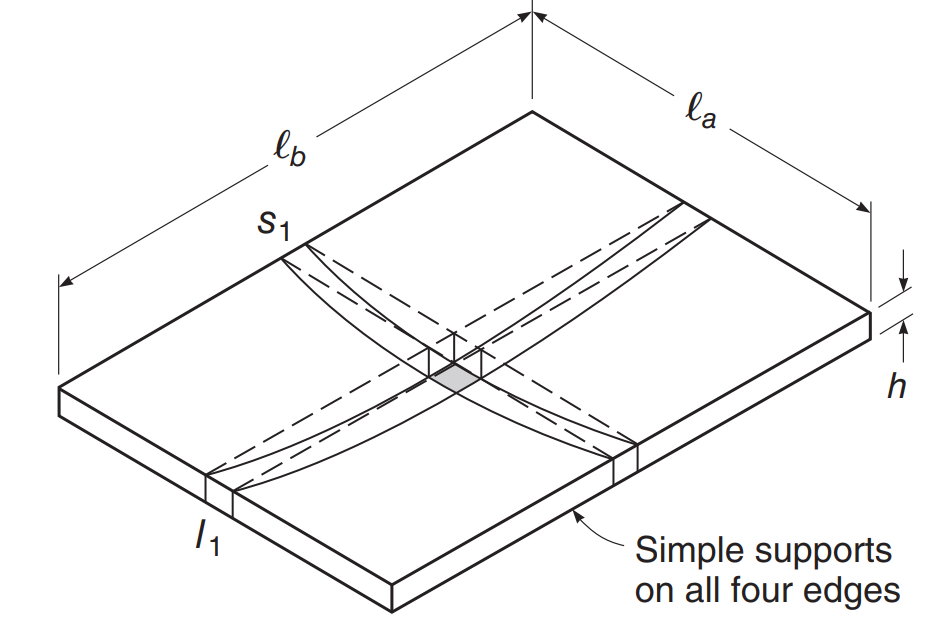
фигура 2. Простой пример двусторонней плиты при изгибе. (Дэвид Дарвин, Чарльз В.Долан, Артур Х. Нильсон, “Проектирование бетонных конструкций,” Пятнадцатое издание, Макгроу-Хилл Образование)
Мы можем определить вертикальное смещение как (\(л_а < фунт \)):
\(\Delta_a = \frac{{5}{ш_а}{л_а^4}}{384{Е}{я}}\)
\(\Delta_b = \frac{{5}{ш_б}{л_б^4}}{384{Е}{я}}\)
Поскольку плита представляет собой непрерывную систему, оба вертикальных отклонения будут иметь одинаковое значение. Мы можем сравнить уравнения, чтобы выразить зависимость между нагрузкой, переносимой в каждом направлении, как функцию размеров в плане..
\(\Delta_a = \Delta_b \to \frac{{5}{ш_а}{л_а^4}}{384{Е}{я}} = frac{{5}{ш_б}{л_б^4}}{384{Е}{я}}\)
\(\гидроразрыва{ш_а}{ш_б} знак равно {(\гидроразрыва{фунт}{л_а}})^4 \)
Все железобетонные нормативы по проектированию плит делятся на односторонние и двусторонние, если частное \(\гидроразрыва{фунт}{л_а}\) больше или меньше значения 2, соответственно.
Используя приведенные выше уравнения, когда \(\гидроразрыва{фунт}{л_а}=2\), нагрузка, переносимая по короткому направлению, равна \(ш_а = {16}{ш_б}\) и когда значение \(\гидроразрыва{фунт}{л_а}=1), нагрузка распределяется одинаково в обе стороны \(ш_а ={ш_б}\).
Моменты односторонних плит
Так, мы видим, что когда частное размерностей больше, чем 2, практически, все нагрузки и изгибающие моменты будут сосредоточены только в коротком направлении. Этот случай представляет собой одностороннее поведение плиты., а максимальный изгибающий момент можно получить для свободно опертой балки единичной ширины.
\(M_{Максимум,1,D}= Гидроразрыва{{ш_а}{1 м}{л_а^2}}{8}\)
Моменты двусторонних плит
Решение случая двусторонней плиты — сложная и ответственная задача строительной механики.. На рисунке ниже вы можете видеть, что общий анализ состоит из пластины с полными силами и моментами в каждом направлении..
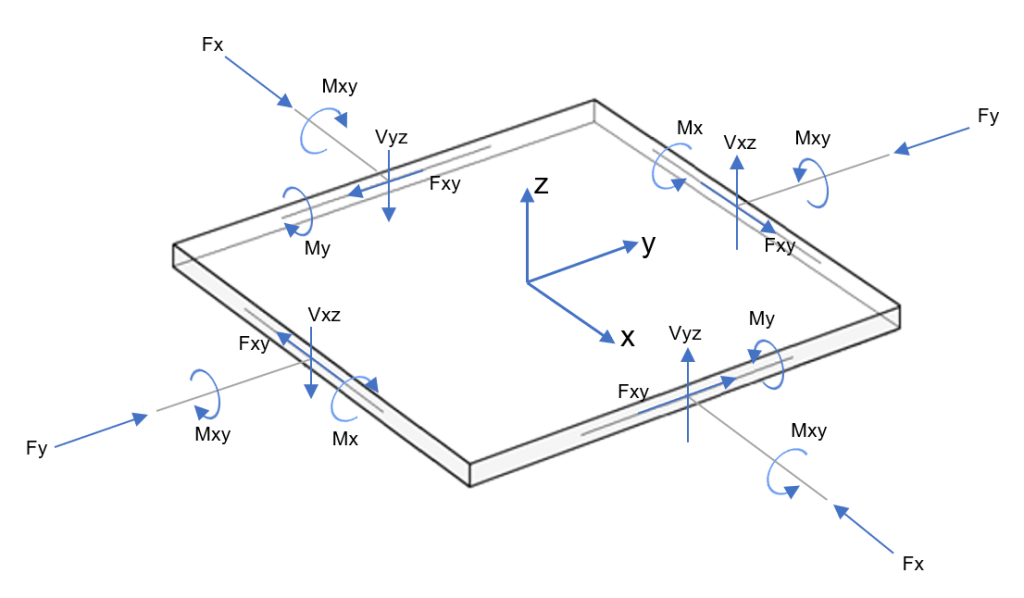
фигура 3. Действия над элементом пластины (изгибающие и крутящие моменты; нормальные и поперечные силы)
Эта трудность связана с тем, что реальная проблема, которую необходимо решить, — это уравнение в частных производных четвертого порядка, которое включает изгиб в двух направлениях.. Форма этого уравнения:
\(\гидроразрыва{\частичный^4{вес}}{{\частичный}{х^4}} + {2}\гидроразрыва{{\частичный^4}{вес}}{{{\частичный}{х^2}}{{\частичный}{у^2}}}+\гидроразрыва{\частичный^4{вес}}{{\частичный}{х^4}}-\гидроразрыва{ф_з}{D} знак равно 0\)
Где жесткость пластины (используя упругие механические и геометрические свойства) является \(D=\frac{{Е}{т^3}}{{12}{(1-\нет^2)}}\).
Аналитическое решение этого уравнения доступно только для простых условий опоры.. Единственный способ получить возможное решение для практических и реальных случаев — это использовать численные методы, такие как метод конечных элементов..
SkyCiv использует этот подход для анализа пластин.. По следующим ссылкам, у вас будет доступ к обучающим материалам, чтобы узнать о характеристиках платформы SkyCiv.: Проектирование пластин в S3D и Как моделировать тарелки? .
Если вы новичок в SkyCiv, Зарегистрируйтесь и протестируйте программу самостоятельно!


