В исполнении со стальным соединением, болты обычно проектируются как группа болтов, которая действует как единое целое, выдерживая заданную нагрузку.. Прочность группы болтов обычно рассчитывается по контролирующей прочности ее наиболее критического болта.. Прямые нагрузки распределяются между общим количеством болтов, в то время как индуцированный момент из-за эксцентриситета нагрузок распределяется в зависимости от момента инерции группы болтов и расстояния от центроида. Этот анализ называется анализом упругости.. Благодаря упрощенным и консервативным предположениям о распределении нагрузки, это часто приводит к перерасчёту болтовых соединений.
Говоря об экономичных и экономичных конструкциях, неэластичный подход предпочитают большинство производителей. Требуется меньшее количество болтов для той же величины нагрузки. Чтобы сделать неэластичный подход, мгновенный центр вращения (ИКОР) метод с использованием итераций - лучший способ.
В этой статье, мы покажем, как рассчитать силу болтовое соединение используя метод ИКОР. Реакции на болт будут рассчитываться по уравнению (7-1) на страницах 7-7 из Руководство AISC, 15-е издание. Затем это будет использоваться для проверки правильности предполагаемого местоположения мгновенного центра группы болтов.. В завершение, как только у нас будет правильное местоположение IC, затем мы рассчитаем коэффициент группы болтов C, чтобы определить его прочность..
Использование метода ICOR для получения коэффициента группы болтов — длительный процесс, поскольку требует метода проб и ошибок для получения мгновенного центра. (IC) место расположения. Настоящее время, с помощью компьютерных решателей, IC группы болтов можно легко рассчитать с помощью запрограммированных итераций.. Решатель группы болтов SkyCiv использует метод быстрой итерации для определения местоположения IC и коэффициента группы болтов за считанные секунды. В настоящее время он реализован в AS 4100 код проектирования, но скоро будет интегрирован в остальные коды проектирования..
Получение свойств группы болтов
Давайте начнем наш простой анализ с группы болтов из четырех болтов, нагруженных эксцентричной вертикальной сдвиговой нагрузкой 10 кипы . Эксцентриситет нагрузки по оси x равен 4 дюймах справа от затворной группы. Угол от вертикали равен нулю, а эксцентриситет по оси Y равен нулю..
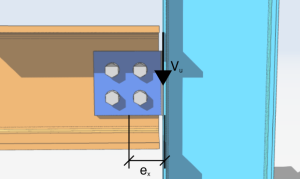
\(V_{U} = 10 тысяч фунтов \)
\(\тета = 0 град)
\(e_{Икс} знак равно 4 в)
\(e_{и} = 0in)
Первое, что нужно сделать, это получить координаты всех болтов в нашей болтовой группе.. Настоятельно рекомендуется использовать визуальные руководства и таблицы..
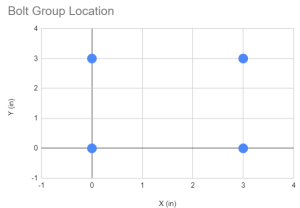
| Идентификатор магазина | Икс (в) | И (в) |
| 1 | 0 | 0 |
| 2 | 0 | 3 |
| 3 | 3 | 0 |
| 4 | 3 | 3 |
Чтобы получить центр тяжести группы затворов вдоль x- и оси Y, нам нужна формула ниже.
Позволять \(N \) = общее количество болтов
\(ИКС_{компьютерная графика} = frac{\сумма Х}{N}\)
\(Y_{компьютерная графика} = frac{\сумма Y}{N} \)
затем, наше решение:
\(ИКС_{компьютерная графика} = frac{\сумма Х}{N} = frac{0 в + 0 в + 3 в + 3 в}{4} знак равно 1.5 в)
\(Y_{компьютерная графика} = frac{\сумма Y}{N} = frac{0 в + 3 в + 0 в + 3 в}{4} знак равно 1.5 в)
Предположим, где находится I.C..
После получения центроида, будем считать местоположение мгновенного центра \(IC). Как первая попытка, можно предположить, что ИС расположена в геометрическом центре тяжести затворной группы.
Так, предполагать
\(ИКС_{IC} = Х_{компьютерная графика} знак равно 1.5 в)
\(Y_{IC} = Y_{компьютерная графика} знак равно 1.5 в)
затем, табулируем смещение каждого болта к месту расположения ИС. Мы можем просто сделать это, получив сначала расстояние по x и расстояние по y., затем получить его смещение
| Идентификатор магазина | сх (в) | су (в) | с (в) |
| 1 | -1.5 | -1.5 | 2.121 |
| 2 | -1.5 | 1.5 | 2.121 |
| 3 | 1.5 | -1.5 | 2.121 |
| 4 | 1.5 | 1.5 | 2.121 |
куда,
\(c_{Икс} = Х_{я} – ИКС_{IC}\)
\(c_{и} = Y_{я} – Y_{IC}\)
\(с = кв.{{\осталось(c_{Икс} \право)}^{2} + {\осталось(c_{и} \право)}^{2}}\)
Для болта №. 1, наше решение
\(c_{Икс} = 0in – 1.5 в = -1.5 в)
\(c_{и} = 0in – 1.5 в = -1.5 в)
\(с = кв.{{\осталось( -1.5 в справа)}^{2} + {\осталось( -1.5 в справа)}^{2}} = 2.121in\)
Рассчитайте деформацию на болт относительно расстояния от IC
следовательно, после получения расстояния болта от предполагаемого местоположения IC, затем мы вычисляем деформацию каждого болта в зависимости от его расстояния.
Максимальная деформация на болт, установлен в \(\Дельта_{Максимум} знак равно 0.34 в), основан на экспериментальных данных для болта ASTM, как описано на странице AISC 7-8. Используя линейную пропорцию, и настройка \(\Дельта_{Максимум} знак равно 0.34 в), мы можем рассчитать деформацию отдельного болта относительно его части на максимальное расстояние \(c_{Максимум}\). Уравнение для получения показано ниже.
\(\Дельта_{1} = 0,34 дюйма раз влево( \гидроразрыва{с}{c_{Максимум}}\право) \)
Для болта №. 1, деформация
\(\Дельта_{1} = 0,34 дюйма раз влево( \гидроразрыва{2.121 в}{2.121 в}\право)\)
Для остальных болтов, расчетные деформации приведены в таблице ниже.
| Идентификатор магазина | \(\Delta\) (в) |
| 1 | 0.34 |
| 2 | 0.34 |
| 3 | 0.34 |
| 4 | 0.34 |
Получить реакции на болт
Как только мы получим деформацию на болт, тогда мы можем использовать AISC 15th Ed. уравнение (7-1) чтобы получить реакции на болт.
\(Р = Р_{ульта} \осталось ( 1 – е ^{-10\Дельта}\право )^{0.55}\)
В \(Р_{ульта}\) в уравнении - предполагаемая предельная нагрузка на болт, которую мы можем установить как прочность болта на сдвиг.
\(Р_{ульта} = фи R_{N} \)
Для нашего примера, мы будем использовать прочность болта на сдвиг \(24.4 кип ). Также допустимо использовать другое значение, так как оно просто аннулируется при расчете коэффициента группы болтов. \(С) позже.
Для болта №. 1, расчетная реакция
\(Р = Р_{ульта} \осталось ( 1 – е ^{-10\Дельта}\право )^{0.55}\)
\(Прочность на единицу размера сварного шва 24.4 кип влево ( 1 – е ^{-10 \раз осталось ( 0.34 в справа )}\право )^{0.55}\)
\(Прочность на единицу размера сварного шва 23.949 кип )
Для остальных болтов, расчетные реакции следующие. В то же время, компоненты болтовой реакции \(Р) вдоль x и y также показаны.
| Идентификатор магазина | р (кип ) | Rx (кип ) | Ry (кип ) |
| 1 | 23.949 | 16.937 | -16.937 |
| 2 | 23.949 | -16.937 | 16.937 |
| 3 | 23.949 | 16.937 | -16.937 |
| 4 | 23.949 | -16.937 | 16.937 |
| ⅀Rx = 0 | ⅀Ру = 0 |
Для болта №1, решения для получения компонентов x и y показаны ниже.
\(Р_{Икс} = -R влево ( \гидроразрыва{c_{и}}{с} \право ) знак равно -23.949 \раз осталось ( \гидроразрыва{-1.5в}{2.121в} \право ) знак равно 23.949 кип )
\(Р_{и} = R влево ( \гидроразрыва{c_{Икс}}{с} \право ) знак равно 23.949 \раз осталось ( \гидроразрыва{1.5в}{2.121в} \право ) знак равно 23.949 кип )
более того, мы должны получить индуцированную моментную нагрузку на болт из-за эксцентриситета. Чтобы вычислить это, мы используем компоненты \(Р_{Икс}\) и \(Р_{и}\) и умножить их на эксцентриситеты \(c_{и}\) и \(c_{Икс}\), соответственно.
Для болта №1, момент реакции на IC
\(M_{р} = -R_{Икс}c_{и} + -Р_{и}c_{Икс} \)
\(M_{р} знак равно -16.937 кипразвлево ( -1.5в справа) + -16.937 кипразвлево ( -1.5 в справа ) \)
\(M_{р} знак равно 50.811 курица)
Для остальных болтов, соответствующие моментные реакции приведены в таблице ниже.
| Идентификатор магазина | г-н (курица) |
| 1 | 50.811 |
| 2 | 0 |
| 3 | 0 |
| 4 | 50.811 |
| ⅀ г = 101.622 |
Проверка местоположения IC
Теперь, когда у нас есть реакции сдвига и момента на болт, мы будем использовать это, чтобы определить величину нагрузки Pu, которой противостоит эта группа болтов.. Сделать это, мы получим равнодействующую суммы всех реакций по x и суммы всех реакций по y.
Из предыдущего раздела, мы рассчитали, что
\(\сумма R_{Икс}=0kip\)
и
\(\сумма R_{и}=0kip\)
Так,
\(П_{U} = кврт{{\осталось( \сумма R_{Икс} \право)}^{2} + {\осталось( \сумма R_{и} \право)}^{2}} знак равно 0 кип )
Так как результирующая нагрузка \(П_{U} = 0кип), на этом этапе мы можем решить не продолжать проверку, поскольку наши данные будут равны нулю.. Мы также можем сделать вывод, что первое предполагаемое местонахождение I.C., который находится в центре тяжести затворной группы, это неверно. тем не мение, для целей этого обсуждения, мы продолжим с шагами ниже.
\(П_{ух} = -P_{U}грехлевый ( \тета право ) знак равно 0 кип \)
\(П_{уй} = -P_{U}кослевый ( \тета право ) знак равно 0 кип \)
\(M_{U} = -P_{ух}\осталось ( Y_{компьютерная графика} + e_{и} – Y_{IC} \право ) + -П_{уй} \осталось (ИКС_{компьютерная графика} + e_{Икс} – ИКС_{IC} \право ) знак равно 0 кип \)
поскольку,
\(П_{ух} \neq сумма R_{Икс} \)
\(П_{уй} \neq сумма R_{и} \)
\(M_{U} \я не М_{р} \)
Следовательно, предполагаемое местонахождение IC. это неверно. Теперь мы можем перейти к следующему предполагаемому местоположению..
SkyCiv имеет полную интеграцию расчета группы болтов в австралийский стандартный модуль.. Хотите попробовать наше программное обеспечение для проектирования соединений?
Вторая итерация
Для нашей второй итерации, допустим, что I.C.. находится по координатам, указанным ниже.
Предполагать
\(ИКС_{IC} знак равно 0.062 в)
\(Y_{IC} знак равно 1.5 в)
затем, давайте выполним шаги, которые мы сделали в нашей первой итерации. В итоге, в таблице ниже будут показаны координаты, расстояние каждого болта от предполагаемого I.C., и соответствующую деформацию относительно расстояния.
| Идентификатор магазина | Икс (в) | И (в) | сх (в) | су (в) | с (в) | \(\Delta\) (в) |
| 1 | 0 | 0 | -0.062 | -1.5 | 1.501 | 0.155 |
| 2 | 0 | 3 | -0.062 | 1.5 | 1.501 | 0.155 |
| 3 | 3 | 0 | 2.938 | -1.5 | 3.299 | 0.34 |
| 4 | 3 | 3 | 2.938 | 1.5 | 3.299 | 0.34 |
Обратите внимание, что рассчитанный центр тяжести затворная группа все то же самое, поскольку в координатах болта ничего не изменилось.
\(ИКС_{компьютерная графика} знак равно 1.5 в)
\(Y_{компьютерная графика} знак равно 1.5 в)
затем, вычисляем реакции вдоль x, реакции вдоль y, и соответствующий момент. Значения приведены в таблице ниже.
| Идентификатор магазина | р (кип ) | Rx (кип ) | Ry (кип ) | г-н (курица) |
| 1 | 21.4 | 21.4 | -0.9 | 32.1 |
| 2 | 21.4 | -21.4 | -0.9 | 32.1 |
| 3 | 23.9 | 10.9 | 21.3 | 79.0 |
| 4 | 23.9 | -10.9 | 21.3 | 79.0 |
| ⅀Rx = 0 | ⅀Ру = 41 | ⅀ г = 222 |
следующий, определяем результирующую нагрузку всех реакций по x и y.
\(П_{U} = кврт{{\осталось( \сумма R_{Икс} \право)}^{2} + {\осталось( \сумма R_{и} \право)}^{2}}\)
\(П_{U} = кврт{{\осталось( 0 кипвправо)}^{2} + {\осталось( 40.703 кипвправо)}^{2}}\)
\(П_{U} знак равно 40.703 кип )
затем, компоненты результирующей нагрузки по заданным \(\тета) показано ниже.
\(П_{ух} = -P_{U}грех влево ( \тета право ) = -41kip times sinleft ( 0 град вправо )знак равно 0 кип )
\(П_{уй} = -P_{U}потому что влево ( \тета право ) = -41kip times cos left ( 0 град вправо )знак равно -41 кип )
Затем мы будем использовать эти компоненты для решения текущей нагрузки о предполагаемой I.C..
\(M_{U} = -P_{ух} \осталось ( Y_{компьютерная графика} + e_{и} – Y_{IC} \право) + П_{уй} \осталось ( ИКС_{компьютерная графика} + e_{Икс} – ИКС_{IC} \право)\)
\(M_{U} знак равно -0 кип влево ( 1.5 в +0 в – 1.5 в справа) + 41 кип влево ( 1.5 в +4 в – 0.06 в справа)\)
\(M_{U} знак равно -222 курица)
следующий, давайте сравним рассчитанное пух, пух, и MU к реакциям затворной группы.
\(П_{ух} \приблизительно – \сумма R_{Икс}\)
\(П_{уй} \приблизительно – \сумма R_{и}\)
\(M_{U} \приблизительно – \сумма М_{U}\)
Так как левая часть почти равна правой части уравнения, можно сказать, что предполагаемое местонахождение I.C.. правильно!
Решение для коэффициента C
Как только I.C.. местоположение определено, теперь мы можем получить коэффициент группы болтов C по формуле ниже.
\(C = гидроразрыв{П_{U}}{\фи Р_{N}} = \frac{40.703 кип }{24.4 кип } знак равно 1.668\)
Бесплатный калькулятор группы болтов
Посмотрите, как мы проектируем наши болтовые соединения с помощью этого подхода, используя наш Бесплатный калькулятор проектирования стальных соединений! Для большей функциональности, подпишитесь на наше программное обеспечение Structural 3D сегодня, чтобы начать!


