Centroid'in Temelleri

Bir kesit üzerinde not etmek önemlidir., alanı boyunca üniform olan, ağırlık merkezi, keyfi olarak ayarlanmış bir eksene göre momentlerin toplamı alınarak bulunabilir., ancak genellikle üst veya alt fiberde ayarlanır. ile ilgili bir önceki makalemize göz atın ağırlık merkezi nasıl bulunur of a beam section and SkyCiv Free Centroid Calculator.

Ücretsiz Centroid Hesap Makinesi

Temelde, ağırlık merkezi, alanın toplamı üzerinden momentlerin toplamı alınarak elde edilebilir.. Bu şekilde ifade edilen.

[matematik]
\bar{x}= frac{1}{Bir}\int xfsol ( x sağ )dx
[matematik]

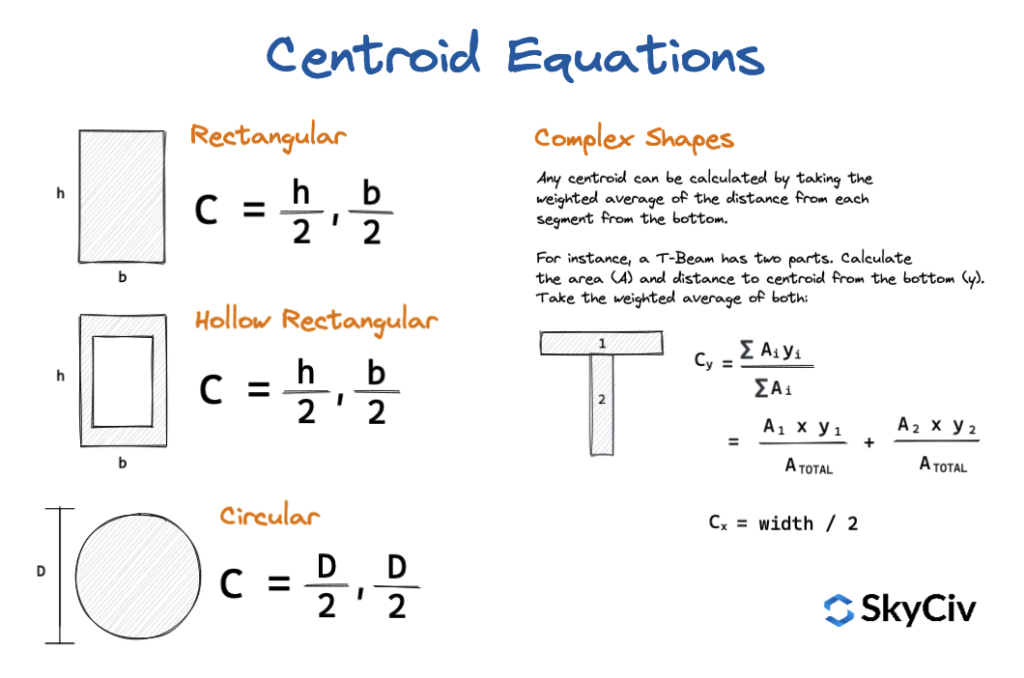
Centroid Denklemlerinin Özeti

Yukarıdaki denklemde, f(x) fonksiyondur ve x moment koludur. Bunu daha iyi göstermek için, tabanı x ekseniyle çakışan keyfi bir üçgenin y ağırlık merkezini türeteceğiz. Bu durumda, üçgenin şekli, eşkenar olsun, ikizkenar veya skalen önemsizdir çünkü her şey yalnızca x eksenine göredir. Üçgenin tabanı eksene göre çakışık veya paralel ise şeklin alakasız olduğuna dikkat edin.. x centroid için çözerken durum böyle olmayacak. Yerine, y eksenine göre iki dik üçgenin ağırlık merkezini almak olarak hayal edebilirsiniz.. Kolaylık uğruna, Aşağıdaki referans tablosuna benzer bir ikizkenar üçgen hayal edelim. b ve h arasındaki ilişkiyi bulmak aşağıdaki ilişkiyi verecektir.

[matematik]
\çatlamak{-Y}{x}= frac{-h}{b}
[matematik]

Üçgenin dik olduğunu hayal ettiğimiz için eğimin negatif olduğuna dikkat edin.. Üçgenin ters çevrildiğini hayal edersek, eğim pozitif olurdu. Ne olursa olsun, ilişki aynı kalır. x = f olarak(Y), yukarıdaki ilişki aşağıdaki gibi yeniden yazılabilir.

[matematik]
x=fsol ( y doğru )= frac{b}{h}Y
[matematik]

Artık centroid için çözebiliriz. Yukarıdaki ilk denklemin ayarlanması, aşağıdakileri alıyoruz.

[matematik]
\bar{Y}= frac{1}{Bir}\int yfsol ( y doğru )iki
[matematik]

Ek değerleri takmak ve yukarıdaki ilişkiyi değiştirmek aşağıdaki denklemi verecektir..

[matematik]
\bar{Y}= frac{2}{bh}\int_{0}^{h} \çatlamak{b}{h}ve ^{2}iki
[matematik]

basitleştirme,

[matematik]
\bar{Y}= frac{2}{h ^{2}}\ayrıldı [ \çatlamak{ve ^{3}}{3} \sağ ]_{0}^{h}
[matematik]
[matematik]
\bar{Y}= frac{2}{h ^{2}}\ayrıldı [ \çatlamak{h ^{3}}{3}-0 \sağ ]
[matematik]
[matematik]
\bar{Y}= frac{2}{3}h
[matematik]

Bu çözümün üstten alındığını unutmayın.. Alttan alınan ağırlık merkezi şuna eşit olmalıdır: 1/3 h'nin.

Yaygın şekillerin ve kiriş kesitlerinin ağırlık merkezleri için formül

Aşağıda bir liste çeşitli kiriş kesit şekilleri ve bölümün ağırlık merkezlerine olan uzaklığı. Denklemler, belirli bir bölümün ağırlık merkezinin tabandan veya bölümün en sol noktasından nasıl bulunacağını gösterir.. SkyCiv Öğrenci ve Yapısal abonelikler için, bu referans, gittiğiniz her yere yanınızda götürmek için bir PDF Referansı olarak da indirilebilir.. Bir kiriş bölümünün ağırlık merkezleri, Nötr Ekseni belirledikleri için son derece önemlidir ve bir kiriş kesitini analiz ederken gerekli olan en erken adımlardan biridir..

SkyCiv ayrıca, kiriş bölümleriyle ilgili tüm denklemleri ve formülleri içeren kapsamlı bir Kesit Özeti Tablosu sunar. (eylemsizlik momenti, alan vb…).

Çeşitli centroidler için denklem aşağıda listelenmiştir.:

REFERANS	CY (Alttan uzaklık)	Cx (En sol noktadan uzaklık)
Dikdörtgen veya Dikdörtgen Bölümlerin Merkez Noktası
	[matematik] \dfrac{h}{2} [matematik]	[matematik] \dfrac{b}{2} [matematik]
İçi Boş Dikdörtgen Kesitin Merkez Noktası
	[matematik] \dfrac{b}{2} [matematik]	[matematik] \dfrac{h}{2} [matematik]
Bir Dairenin veya Dairesel Kesitin Merkez Noktası
	[matematik] \dfrac{D}{2} [matematik]	[matematik] \dfrac{D}{2} [matematik]
Bir İçi Boş Dairesel Kesitin Merkez Denklemi
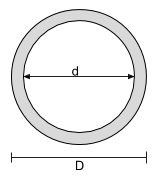	[matematik] \dfrac{D}{2} [matematik]	[matematik] \dfrac{D}{2} [matematik]
İkizkenar Üçgenin Merkez Noktası
	[matematik] \dfrac{h}{3} [matematik]	[matematik] \dfrac{b}{2} [matematik]
Bir I Kirişinin Merkez Noktası
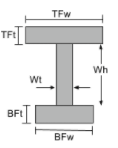	[matematik] \çatlamak{TFw times TFt times left ( BFt + Wh + \çatlamak{TFt}{2} \sağ )}{TFwtime TFt + Ağırlıkkez Wh + BFwkez BFt} + [matematik] [matematik] \çatlamak{Wt times Wh times left ( BFt + \çatlamak{Wh}{2} \sağ )}{TFwtime TFt + Ağırlıkkez Wh + BFwkez BFt} + [matematik] [matematik] \çatlamak{BFw times BFt times left ( \çatlamak{BFt}{2} \sağ )}{TFwtime TFt + Ağırlıkkez Wh + BFwkez BFt} [matematik]	[matematik] TFw > BFw, \çatlamak{TFw}{2}[matematik] [matematik] BFw > TFw, \çatlamak{BFw}{2} [matematik]
Bir T-Kesitinin Merkez Noktası
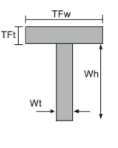	[matematik] \çatlamak{Wt times Wh times left ( \çatlamak{Wh}{2} \sağ )}{TFwtime TFt + Ağırlıkkez Wh } + [matematik] [matematik] \çatlamak{TFw times TFt times left ( Wh + \çatlamak{TFt}{2} \sağ ) }{TFwtime TFt + Ağırlıkkez Wh } [matematik]	[matematik] \çatlamak{TFw}{2} [matematik]
Bir C-Bölümünün Merkezi
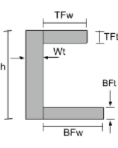	[matematik] \çatlamak{TFw times TFt times left ( h – \çatlamak{TFt}{2} \sağ )}{TFwtime TFt + Ağırlıkkez Wh + BFwkez BFt} + [matematik] [matematik] \çatlamak{Ağırlıkkez sakez sol ( \çatlamak{h}{2} \sağ )}{TFwtime TFt + Ağırlıkkez Wh + BFwkez BFt} + [matematik] [matematik] \çatlamak{BFw times BFt times left ( \çatlamak{BFt}{2} \sağ )}{TFwtime TFt + Ağırlıkkez Wh + BFwkez BFt} [matematik]	[matematik] \çatlamak{TFttimes TFwtimes sol ( Wt + \çatlamak{TFw}{2} \sağ )}{TFtkez TFw + hkez Ağırlık + BFtkez BFw} + [matematik] [matematik] \çatlamak{htimes Wttimes sol ( \çatlamak{Wt}{2} \sağ )}{TFtkez TFw + hkez Ağırlık + BFtkez BFw} + [matematik] [matematik] \çatlamak{BFt times BFw times left ( Wt + \çatlamak{BFw}{2} \sağ )}{TFtkez TFw + hkez Ağırlık + BFtkez BFw} [matematik]
Açıların Merkez Noktası
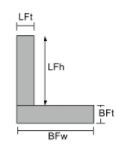	[matematik] \çatlamak{LFttimes LFhtimes sol ( BFt + \çatlamak{LFh}{2} \sağ ) }{LFttimes LFh + BFwkez BFt} + [matematik] [matematik] \çatlamak{BFw times BFt times left ( \çatlamak{BFt}{2} \sağ )}{LFttimes LFh + BFwkez BFt} [matematik]	[matematik] \çatlamak{LFhtimes LFttimes sol ( \çatlamak{LFt}{2} \sağ )}{LFhtimes LFt + BFtkez BFw} + [matematik] [matematik] \çatlamak{BFt times BFw times left ( \çatlamak{BFw}{2} \sağ )}{LFhtimes LFt + BFtkez BFw} [matematik]

Kirişin Ağırlık Merkezi için Otomatik Denklemler

göz atın Ücretsiz Centroid Hesap Makinesi, basitleştirilmiş bir versiyonu SkyCiv Bölüm Oluşturucu, el hesaplamalarına gerek kalmadan ışının ağırlık merkezini otomatik olarak hesaplamak için. Veya başlamak için bugün kaydolun!

Ücretsiz Başlayın