Основы центроида
Важно отметить, что на поперечном сечении, чья площадь однородна по всей, центроид может быть найден путем суммирования моментов относительно произвольно установленной оси, но обычно устанавливается на верхнем или нижнем волокне. Ознакомьтесь с нашей предыдущей статьей о Эта статья проведет вас через простой процесс расчета центроида сечения балки и бесплатный калькулятор центроидов SkyCiv.
В корне, центр тяжести может быть получен путем суммирования моментов по сумме площади. Что выражается таким образом.
[математический]
\бар{Икс}= Гидроразрыва{1}{А}\интервал xfвлево ( х вправо )дх
[математический]
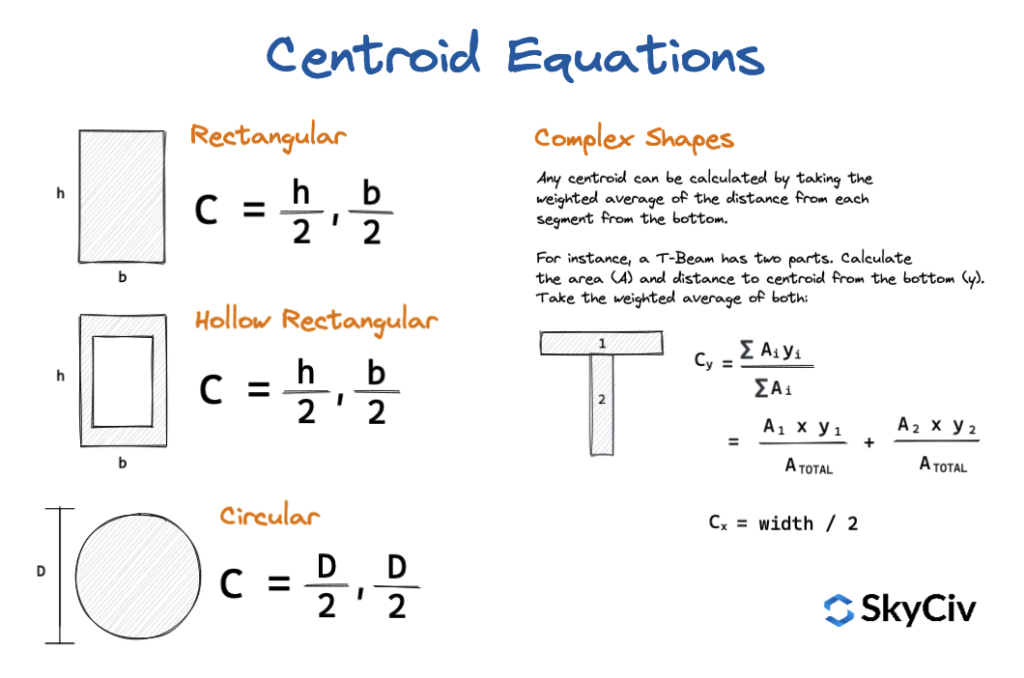
Краткое изложение уравнений центроида
В уравнении выше, е(Икс) - функция, а x - плечо момента. Чтобы лучше проиллюстрировать это, мы получим центр тяжести y произвольного треугольника, основание которого совпадает с осью x. В этой ситуации, форма треугольника, будь то равносторонний, равнобедренный или разносторонний не имеет значения, так как все относительно только оси x. Обратите внимание, что форма не имеет значения, если основание треугольника совпадает или параллельно оси.. Этого не будет при решении для центроида x. Вместо, вы можете представить это как получение центроида двух прямоугольных треугольников относительно оси y. Ради удобства, давайте представим себе равнобедренный треугольник, подобный справочной таблице ниже. Нахождение связи между b и h даст следующее соотношение.
[математический]
\гидроразрыва{-и}{Икс}= Гидроразрыва{-час}{б}
[математический]
Обратите внимание, что наклон отрицательный, так как мы представляем треугольник вертикальным.. Если представить треугольник перевернутым, наклон будет положительным. Несмотря на, отношения остаются прежними. Поскольку x = f(и), приведенное выше отношение можно переписать следующим образом.
[математический]
х = е влево ( у право )= Гидроразрыва{б}{час}и
[математический]
Теперь мы можем найти центроид. Настройка первого уравнения выше, мы получаем следующее.
[математический]
\бар{и}= Гидроразрыва{1}{А}\int yf left ( у право )два
[математический]
Добавление дополнительных значений и замена приведенного выше отношения приведет к следующему уравнению.
[математический]
\бар{и}= Гидроразрыва{2}{ЬН}\int_{0}^{час} \гидроразрыва{б}{час}и ^{2}два
[математический]
Упрощая,
[математический]
\бар{и}= Гидроразрыва{2}{ч ^{2}}\осталось [ \гидроразрыва{и ^{3}}{3} \право ]_{0}^{час}
[математический]
[математический]
\бар{и}= Гидроразрыва{2}{ч ^{2}}\осталось [ \гидроразрыва{ч ^{3}}{3}-0 \право ]
[математический]
[математический]
\бар{и}= Гидроразрыва{2}{3}час
[математический]
Обратите внимание, что это решение взято сверху. Центроид, взятый снизу, должен тогда быть равен 1/3 ч.
Формула для центроидов обычных форм и сечений балок
Ниже приведен список разнообразие форм сечения балки и расстояние до центроидов сечения. Уравнения показывают, как найти центроид определенной секции от основания или самой дальней левой точки секции.. Для подписок SkyCiv Student и Structural, этот справочник также можно загрузить в виде справочника в формате PDF, чтобы взять его с собой куда угодно. Центроиды сечения балки чрезвычайно важны, поскольку они определяют нейтральную ось и являются одним из первых шагов, необходимых при анализе сечения балки..
SkyCiv также предлагает исчерпывающую сводную таблицу разделов, которая содержит все уравнения и формулы, относящиеся к сечениям балки. (момент инерции, площадь и т. д.…).
Уравнения для различных центроидов приведены ниже.:
| ССЫЛКА | Си (Расстояние снизу) |
СИкс (Расстояние от самой дальней левой точки) |
Центроид прямоугольника или прямоугольного сечения |
||
|---|---|---|
 |
[математический] \dfrac{час}{2} [математический] |
[математический] \dfrac{б}{2} [математический] |
Центроид полого прямоугольного сечения. |
||
 |
[математический] \dfrac{б}{2} [математический] |
[математический] \dfrac{час}{2} [математический] |
Центроид круга или кругового сечения |
||
 |
[математический] \dfrac{D}{2} [математический] |
[математический] \dfrac{D}{2} [математический] |
Уравнение центроида полого кругового сечения. |
||
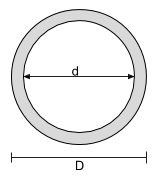 |
[математический] \dfrac{D}{2} [математический] |
[математический] \dfrac{D}{2} [математический] |
Центроид равнобедренного треугольника |
||
 |
[математический] \dfrac{час}{3} [математический] |
[математический] \dfrac{б}{2} [математический] |
Центроид двутавровой балки |
||
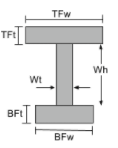 |
[математический] \гидроразрыва{TFw times TFt times left ( BFT + белый + \гидроразрыва{Tft}{2} \право )}{TFw раз TFt + Вт раз Wh + BFw times BFt} + [математический] [математический] \гидроразрыва{Wt times Wh times left ( BFT + \гидроразрыва{белый}{2} \право )}{TFw раз TFt + Вт раз Wh + BFw times BFt} + [математический] [математический] \гидроразрыва{BFw times BFt times left ( \гидроразрыва{BFT}{2} \право )}{TFw раз TFt + Вт раз Wh + BFw times BFt} [математический] |
[математический] TFW > BFW, \гидроразрыва{TFW}{2}[математический] [математический] BFW > TFW, \гидроразрыва{BFW}{2} [математический] |
Центроид Т-образного сечения |
||
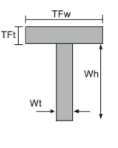 |
[математический] \гидроразрыва{Wt times Wh times left ( \гидроразрыва{белый}{2} \право )}{TFw раз TFt + Вт раз Wh } + [математический] [математический] \гидроразрыва{TFw times TFt times left ( белый + \гидроразрыва{Tft}{2} \право ) }{TFw раз TFt + Вт раз Wh } [математический] |
[математический] \гидроразрыва{TFW}{2} [математический] |
Центроид кесарева сечения |
||
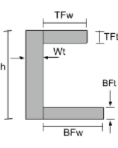 |
[математический] \гидроразрыва{TFw times TFt times left ( час – \гидроразрыва{Tft}{2} \право )}{TFw раз TFt + Вт раз Wh + BFw times BFt} + [математический] [математический] \гидроразрыва{Wt times h times left ( \гидроразрыва{час}{2} \право )}{TFw раз TFt + Вт раз Wh + BFw times BFt} + [математический] [математический] \гидроразрыва{BFw times BFt times left ( \гидроразрыва{BFT}{2} \право )}{TFw раз TFt + Вт раз Wh + BFw times BFt} [математический] |
[математический] \гидроразрыва{TFt times TFw times left ( вес + \гидроразрыва{TFW}{2} \право )}{TFt раз TFw + ч раз Wt + BFt раз BFw} + [математический] [математический] \гидроразрыва{h times Wt times left ( \гидроразрыва{вес}{2} \право )}{TFt раз TFw + ч раз Wt + BFt раз BFw} + [математический] [математический] \гидроразрыва{BFt times BFw times left ( вес + \гидроразрыва{BFW}{2} \право )}{TFt раз TFw + ч раз Wt + BFt раз BFw} [математический] |
Центроид углов |
||
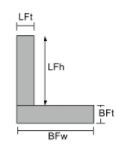 |
[математический] \гидроразрыва{LFt times LFh times left ( BFT + \гидроразрыва{LFH}{2} \право ) }{LFt раз LFh + BFw times BFt} + [математический] [математический] \гидроразрыва{BFw times BFt times left ( \гидроразрыва{BFT}{2} \право )}{LFt раз LFh + BFw times BFt} [математический] |
[математический] \гидроразрыва{LFh times LFt times left ( \гидроразрыва{LFt}{2} \право )}{LFh раз LFt + BFt раз BFw} + [математический] [математический] \гидроразрыва{BFt times BFw times left ( \гидроразрыва{BFW}{2} \право )}{LFh раз LFt + BFt раз BFw} [математический] |
Автоматические уравнения для центроида балки
Проверьте наши Эта статья проведет вас через простой процесс расчета центроида, упрощенная версия SkyCiv Раздел Строитель, автоматически рассчитать центр тяжести балки без необходимости ручных вычислений. Или зарегистрируйтесь сегодня, чтобы начать!


