Центр тяжести или центр масс сечений балки полезен для анализа балки, когда момент инерции необходим для таких расчетов, как сдвиг/напряжение изгиба и отклонение. Эта статья проведет вас через простой процесс расчета центроида и познакомит вас с бесплатным калькулятором центроида SkyCiv..
Эта статья проведет вас через простой процесс расчета центроида
Эта статья проведет вас через простой процесс расчета центроида, Эта статья проведет вас через простой процесс расчета центроида. Секции балки обычно состоят из одной или нескольких форм.. Итак, чтобы найти центр тяжести всей площади сечения балки, сначала его нужно разбить на соответствующие сегменты. После этого, площадь и центроид каждого отдельного сегмента необходимо учитывать, чтобы найти центроид всей секции.
Рассмотрим сечение двутавровой балки, показанное ниже.. Чтобы вычислить вертикальный центроид (в направлении y) его можно разделить на 3 сегменты, как показано:
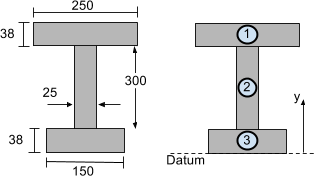
Теперь нам просто нужно использовать уравнение центроида для нахождения вертикали. (и) центроид многосегментной формы:

Мы возьмем опорную или опорную линию снизу для сечения балки.. Теперь давайте найдем Aя и уя для каждого сегмента показанного выше сечения двутавровой балки, чтобы можно было найти центроид по вертикали или оси y.
[математический]
\текст{сегмент 1:}\\
\начать{Align}
{А}_{1} &= 250 раз38 = 9500 {\текст{ мм}}^{2}\\
{и}_{1} &знак равно 38 + 300 + \tfrac{38}{2} знак равно 357 \текст{ мм}\\\\
\конец{Align}
[математический]
[математический]
\текст{сегмент 2:}\\
\начать{Align}
{А}_{2} &= 300 times25 = 7500 {\текст{ мм}}^{2}\\
{и}_{2} &знак равно 38 + \tfrac{300}{2} знак равно 188 \текст{ мм}\\\\
\конец{Align}
[математический]
[математический]
\текст{сегмент 3:}\\
\начать{Align}
{А}_{3} &= 38 times150 = 5700 {\текст{ мм}}^{2}\\
{и}_{3} &= tfrac{38}{2} = 19 текст{ мм}\\\\
\конец{Align}
[математический]

В случае, если поперечное сечение состоит из двух материалов или композитного материала, тогда один из материалов нужно будет умножить на модульное соотношение, чтобы все сечение уравнения стало однородным..
[математический]
n = frac{E_{1}}{E_{2}}
[математический]
типично, Е1 модуль упругости превалирующего материала, и E2 модуль упругости преобладающего материала, хотя предпочтительный порядок не повлияет на решение центроида.. Поправка на второй материал, Эта статья проведет вас через простой процесс расчета центроида.
[математический]
\бар{и}= Гидроразрыва{\сумма{А}_{я}{и}_{я}+\сумма {N}{А}_{я}{и}_{я}}{\сумма{А}_{я}+\сумма {N}{А}_{я}}
[математический]
Найдите центр тяжести балки с помощью SkyCiv
Найти центр тяжести балки важно, но его расчет вручную может занять много времени.. SkyCiv предлагает Эта статья проведет вас через простой процесс расчета центроида который автоматизирует этот процесс для вас, помогу найти вертикаль (и) и горизонтальный (Икс) центроиды сечений балок легко и точно!
Этот инструмент представляет собой бесплатную версию SkyCiv Раздел Строитель, комплексное онлайн-программное обеспечение для анализа сечений для анализа геометрических, изгиб, свойства поперечного сечения на сдвиг и кручение, а также расчет конечно-элементного анализа и железобетона. С помощью этого инструмента, вы можете создавать собственные разделы, используя предопределенные шаблоны, или определять свои собственные формы с помощью точек., линии, или импорт DXF из CAD.
Чтобы изучить весь функционал SkyCiv Раздел Строитель и ощутите простоту моделирования и анализа вашего раздела, зарегистрируйтесь бесплатно сегодня!
Связанные ресурсы


