Как рассчитать неопределенный луч – Метод двойного интеграла

Неопределенный балки может быть проблемой из-за дополнительных шагов, необходимых для решения реакций. Помните, что неопределенные структуры обладают так называемой степенью неопределенности.. Чтобы решить структуру, необходимо ввести граничные условия. следовательно, тем выше степень неопределенности, тем больше граничных условий необходимо определить. Но прежде чем мы сможем решить неопределенную балку, сначала нам нужно определить, является ли луч статически неопределимым. Поскольку балки представляют собой одномерные конструкции, достаточно использовать уравнение для определения внешне статически неопределимых конструкций.

[математический]
я_{е}=R-влево ( 3+e_{с} \право )
[математический]

куда:

• я_е = Степень неопределенности
• R = общее количество реакций
• е_с = Внешние условия (например. внутренний шарнир)

типично, тем не мение, без необходимости решать степень неопределенности, все, кроме простых пролетов или консольных балок, является статически неопределимым., при условии, что такие балки не имеют внутренних шарниров.

Есть много способов подойти к решению неопределенных балок.. Хотя для простоты и сходства с SkyCiv Beam ручные расчеты, мы обсудим метод двойной интеграции.

Двойная интеграция

Двойное интегрирование, пожалуй, самый простой из всех методов анализа балок.. Концепция этого метода довольно проста в отличие от других методов, поскольку он в основном опирается на базовое понимание интегрального исчисления., отсюда и название. Немного интегрального расчета адаптировано из отношения кривизны балки к моменту, который показан ниже..

[математический]
\гидроразрыва{1}{\ро}= Гидроразрыва{M}{Нет}
[математический]

Обратите внимание, что 1/ρ — это кривизна балки, а ρ — радиус кривой.. В корне, определение кривизны - это скорость изменения касательной по отношению к длине дуги. Поскольку момент является функцией нагрузки по отношению к длине элемента, интегрирование кривизны по длине элемента даст наклон балки.. так же, интегрирование наклона по длине элемента даст прогиб балки.. Поскольку типичные структурные нагрузки носят алгебраический характер., Интегрировать эти выражения так же просто, как использовать общую формулу степени.

[математический]
\интервал fвлево ( х вправо )^{N}dx=разрыв{евлево ( х вправо )^{п+1}}{п+1}+С
[математический]

Возможно, лучший способ понять эту концепцию — предоставить пример балки со следующими данными:.

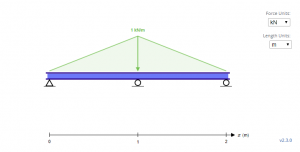
Образец балки выше представляет собой неопределенную балку с треугольными нагрузками.. С опоры, А_и, В_и и С_и во-первых, второй, и третья опоры соответственно, Первый шаг в решении этих неизвестных — начать с уравнений равновесия.

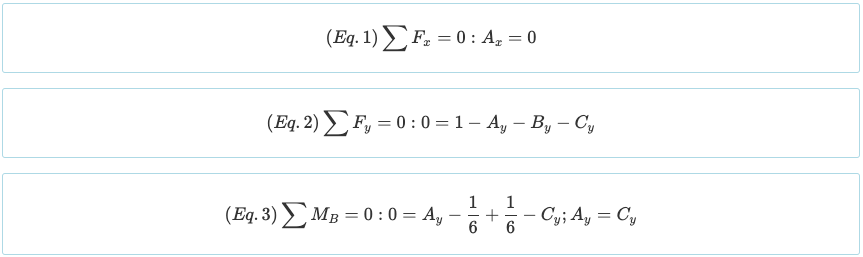
Обратите внимание, что луч имеет степень статическая неопределенность 1°. Так как есть четыре неизвестных (А_Икс, А_и, В_и, и С_и) и есть три уравнения, далекие от приведенных выше уравнений равновесия, необходимо составить еще одно уравнение из граничных условий. Напомним, что момент, создаваемый точечной и треугольной нагрузкой, равен:.

Затем профиль выдавливается на единицу измерения, что позволяет контролировать его длину при создании экземпляра в окончательном документе проекта Revit.:

[математический]
M=Ftimes x; М = Форекс
[математический]

Треугольная нагрузка:

[математический]
M=ГРП{ш_{0}\раз х}{2}\раз осталось ( \гидроразрыва{Икс}{3} \право ); M = frac{ш_{0}х^{2}}{6}
[математический]

Используя метод двойного интегрирования, эти новые уравнения составлены и отображены ниже.

Заметка: Приведенные выше уравнения записаны в виде функций Маколея, где выражение равно нулю, когда Икс < L. В таком случае, L = 1.

В приведенных выше уравнениях, обратите внимание, что добавленный четвертый член появляется из ниоткуда. по факту, направление нагрузки противоположно направлению силы тяжести. Это связано с тем, что уравнения для треугольных нагрузок работают только тогда, когда нагрузка поднимается по мере увеличения длины.. Это не представляет большой проблемы для уравнений для распределенный и точечные нагрузки из-за их симметрии. В результате, эквивалентная нагрузка для балки выше выглядит так же, как и для балки внизу, таким образом, уравнения основаны на этом.

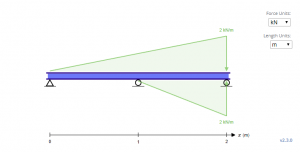
Решить на С₁ и С₂, необходимо определить граничные условия. В луче выше, можно заметить, что три таких граничных условия существуют при Икс знак равно 0, Икс знак равно 1, и Икс знак равно 2, где отклонение y равно нулю в трех местах.

Граничное условие 1

[математический]
х=0, у=0; C_{2}= 0
[математический]

Граничное условие 2

[математический]
х=0, у=0; C_{1}= Гидроразрыва{1}{120}-\гидроразрыва{A_{и}}{6}
[математический]

После определения значений каждой константы, последнее уравнение теперь можно получить, используя последнее граничное условие.

Граничное условие 3

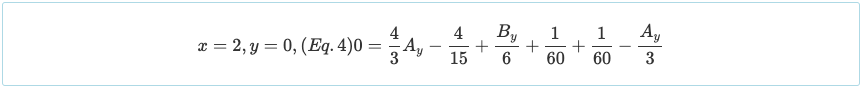
Заметим, что граничное условие θ = 0 при x = 1 может быть использован, хотя он применим только для средней реакции симметричной неразрезной балки с симметричным нагружением.

Поскольку четыре уравнения были определены, теперь их можно решать одновременно. Решение этих уравнений приведет к следующим реакциям.

С реакциями определены, значения реакций можно подставить обратно в уравнение моментов. Это позволит определить значение момента в любой части балочной системы..

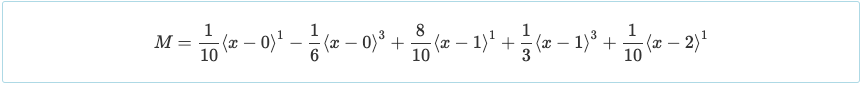
Еще одно удобство двойного интегрирования заключается в том, что уравнение момента представлено таким образом, что его можно использовать для расчета сдвига с помощью соотношения, показанного ниже..

[математический]
V=разрыв{дМ}{дх}
[математический]

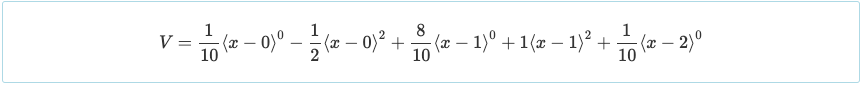
Очередной раз, используя только базовое понимание дифференциального исчисления, приравнивание производной функции нулю дает максимум или минимум этой функции.. таким образом, приравнивая V = 0 приведет к максимальному положительному моменту при Икс знак равно 0.447 и Икс знак равно 1.553 М = 0.030

Конечно, все это можно проверить с помощью SkyCiv Beam.

Программное обеспечение SkyCiv Beam

Программное обеспечение для анализа лучей SkyCiv позволяет пользователям легко и точно анализировать балочные конструкции. Вы можете получить анализ вашего балочного члена, включая реакции, сдвигающая сила, изгибающий момент, отклонение, и подчеркивает в считанные секунды.

Если вы хотите сначала попробовать, Бесплатный Калькулятор Луча отличный способ начать, или просто зарегистрируйтесь бесплатно сегодня!