Полностью проработанный пример наземного Расчет ветровой нагрузки и давления снега на солнечные панели с использованием ASCE 7-16
С последними тенденциями использования возобновляемых источников энергии для сдерживания последствий изменения климата, одной из быстрорастущих отраслей в качестве решения этой проблемы является использование солнечной энергии.. более того, солнечные панели также становятся популярными среди бытовых потребителей в качестве альтернативного источника энергии, поскольку за последние несколько лет электричество резко возросло.. В результате, установка солнечных панелей на крышах домов и строительство солнечных ферм, использующих наземные солнечные панели, увеличивается в количестве. Необходимость расчета ветровой нагрузки на солнечные панели, а также давления снега имеет решающее значение для обеспечения долговечности.. В этой статье, мы обсудим, как рассчитать снеговую и ветровую нагрузку на наземные солнечные панели с помощью ASCE. 7-16.
SkyCiv автоматизирует расчеты скорости ветра с помощью нескольких параметров.. Попробуйте наши Калькулятор ветровой нагрузки солнечной панели
Данные структуры
В этом примере, мы будем использовать следующие данные:
Стол 1. Данные о здании, необходимые для расчета ветровой и снеговой нагрузки.
| Расположение | 395 Рокки Пойнт Роуд, Кордова, Мемфис, Теннесси |
| Заполняемость | Разное – солнечная панель |
| местность | Плоские сельхозугодья |
| Размеры солнечной панели | 16.25 фут |
| Размеры солнечной панели | 13.33 фут |
| Размеры солнечной панели | 8.33 фут |
| Размеры солнечной панели | 30° |
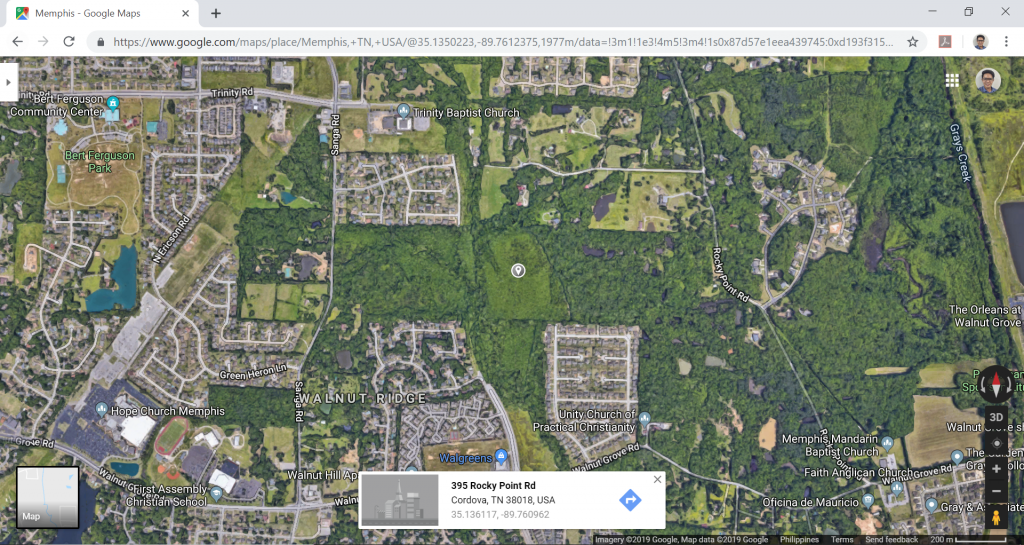
фигура 1. Местонахождение площадки (из Google Maps).
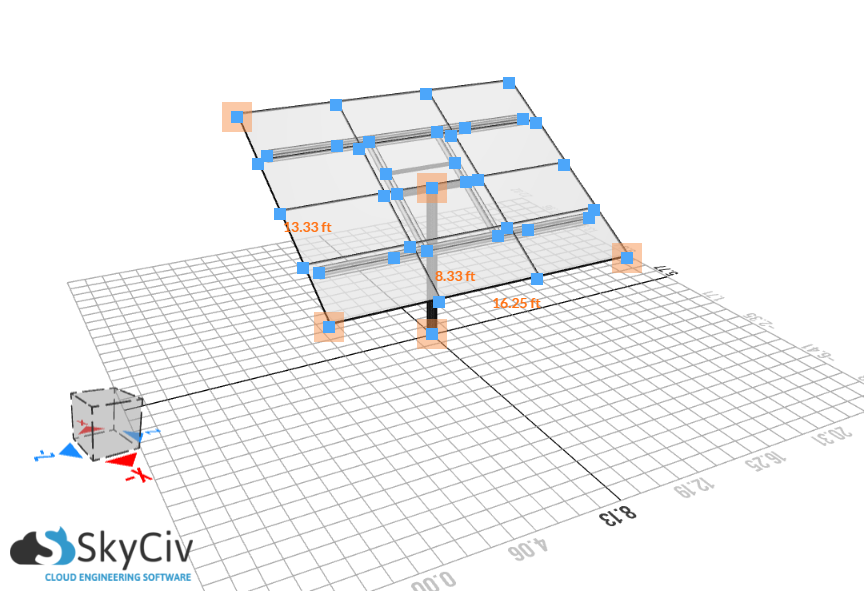
фигура 2. Размеры солнечной панели.
Сборки и шаблоны
При расчете ветровой нагрузки на солнечные панели, мы будем использовать ASCE 7-16 глава 27 – Ветровая нагрузка – Направленная процедура. Наземную солнечную панель будем рассматривать как открытое здание с односкатной крышей при угле наклона меньше или равном 45° и как сплошной знак при угле наклона более 45°..
Формула для определения расчетного ветрового давления выглядит следующим образом.:
Для угла наклона ≤ 45° (рассматривается как открытое здание с односкатной крышей):
\(p = {q}_{h}G{C}_{N}\) (1)
Для угла наклона > 45° (считается сплошным знаком):
\(p = {q}_{h}G{C}_{f}\) (2)
куда:
\(G\) = фактор влияния порывов
\({C}_{N}\) = коэффициент полезной силы для открытой односкатной крыши
\({C}_{f}\) = коэффициент чистой силы для сплошных знаков
\({q}_{h}\) = скоростное давление на контрольной высоте, \(h\), в ПСФ, определяется по формуле:
\({q}_{h} = 0.00256{K}_{z}{K}_{zt}{K}_{d}{K}_{e}V^2\) (3)
\({K}_{z}\) = коэффициент скорости давления
\({K}_{zt}\)= топографический фактор
\({K}_{d}\) = коэффициент направленности ветра
\({K}_{e}\) = коэффициент высоты земли
\(V \) = базовая скорость ветра в милях в час
Обратите внимание, что для угла наклона > 45°, Мы используем размеры вертикальной проекции солнечной панели, а затем используем формулу для коэффициентов чистой силы для сплошных знаков.. Мы углубимся в детали каждого параметра ниже.
Категория риска
Первым шагом является определение категории риска солнечной панели на основе использования или занятости.. Из таблицы 1.5-1 ASCE 7-16, мы можем отнести наземную солнечную панель в этом примере к категории риска I..
Основная скорость ветра, \(V\)
ASCE 7-16 обеспечивает карту ветра, где соответствующая базовая скорость ветра местоположения может быть получена из рисунков 26.5-1A-1C. Из рисунка 26.5-1A, Кордова, Мемфис, Теннесси как-то рядом, где красная точка на рисунке 3 ниже, и оттуда, основная скорость ветра, \(V\), является 100 миль / ч. Обратите внимание, что базовое значение скорости ветра интерполируется из ближайших контуров ветра..
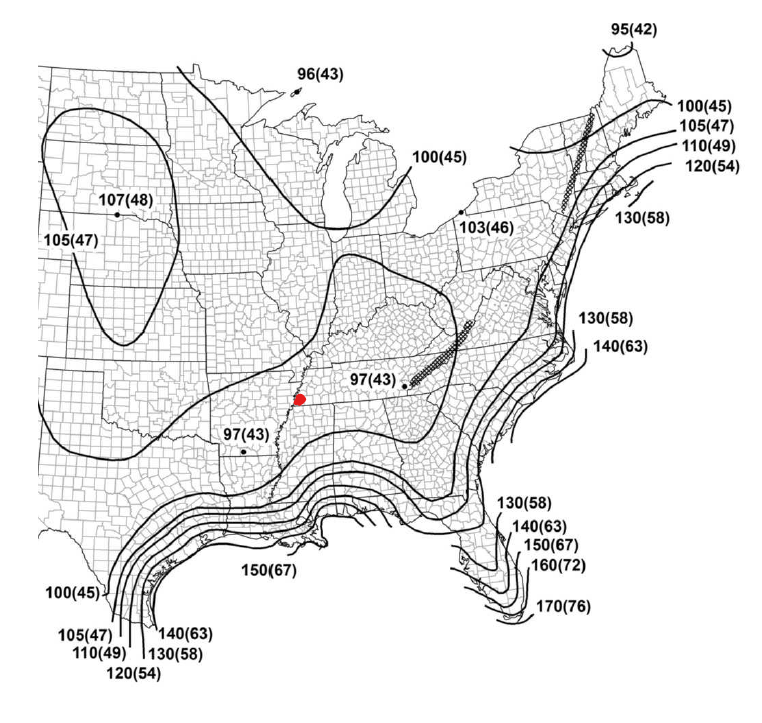
фигура 3. Базовая карта скорости ветра из рисунка 26.5-1A ASCE. 7-16 (Категория риска I) с красной точкой, чтобы указать местоположение нашей солнечной панели.
SkyCiv автоматизирует расчеты скорости ветра с помощью нескольких параметров.. Попробуйте наши Калькулятор ветровой нагрузки солнечной панели
Категория экспозиции
В зависимости от анализируемого направления ветра, категория воздействия солнечной панели определяется из сектора 45° с наветренной стороны на основании раздела 26.7 ASCE 7-16. более того, Раздел C26.7 содержит аэрофотоснимки, показывающие примеры экспозиции B., С, и D на рисунках с C26.7-5 по C26.7-7..
В этом примере, мы будем использовать только ветер, дующий с южного направления. следовательно, на основе примеров аэрофотосъемки, мы можем классифицировать местность с наветренной стороны до экспозиции C на основании рисунка C26.7-6.(б) или “Открытая местность с разбросанными препятствиями высотой, как правило, менее 30 фут (9.1 м)” как показано на рисунке 4 ниже. Мы будем использовать категорию воздействия при расчете коэффициента скорости и давления. \({K}_{z}\)охватывать> и/или топографический фактор \({K}_{zt}\) если нужно.
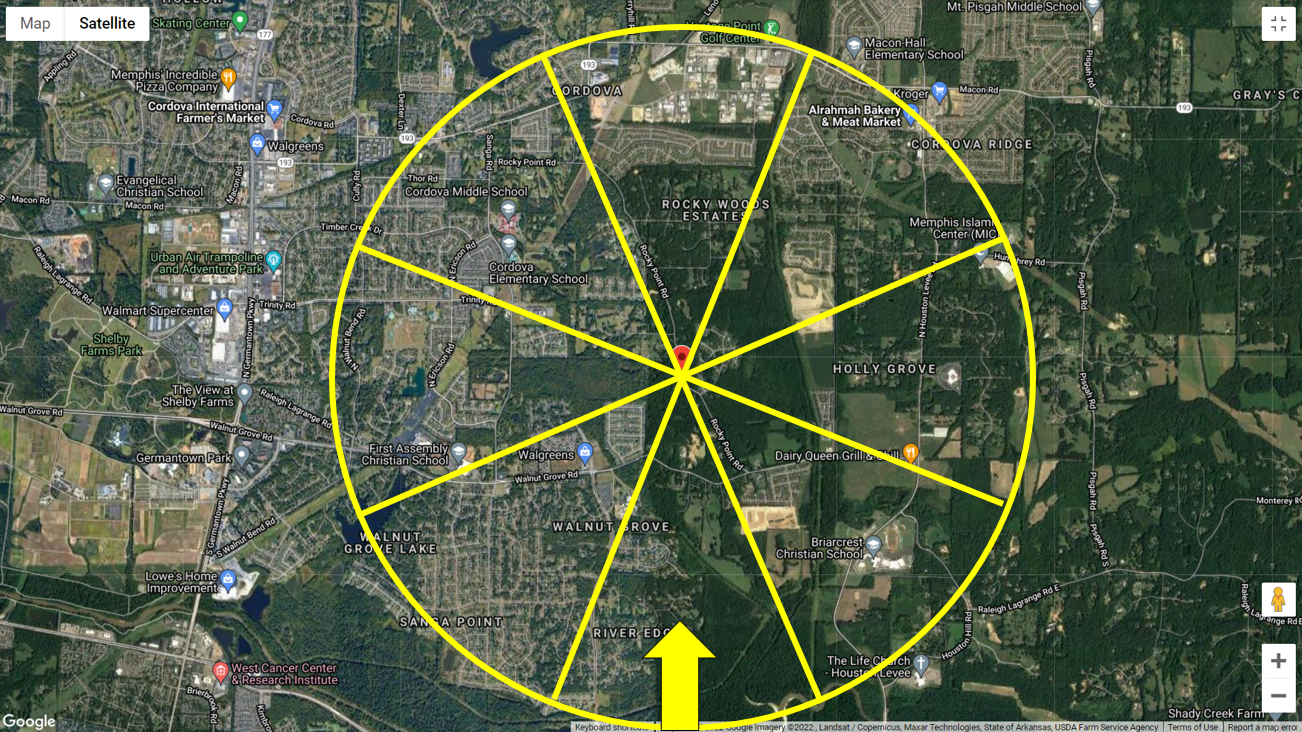
фигура 4. Аэрофотоснимок местности при ветре с юга..
Коэффициент направленности ветра, \( {K}_{d} \)
Фактор направленности ветра, \({K}_{d} \), для солнечной панели равно 0.85 так как солнечная панель может рассматриваться как MWFRS (asce7) когда угол наклона меньше или равен 45° и сплошным знаком для угла наклона больше 45° на основании таблицы 26.6-1 ASCE 7-16.
Коэффициент возвышения земли, \( {K}_{e} \)
Коэффициент возвышения, \({K}_{e} \), можно рассчитать с помощью таблицы 26.9-1 ASCE 7-16. Для этого примера, так как высота площадки равна 350.48 фут, \({K}_{e} \) можно рассчитать по формуле:
\( {K}_{e} = {e}^{-0.0000362{z}_{g}} \) (4)
\( {K}_{e} = {e}^{-0.0000362(350.48)} = 0.987\)
\( {K}_{e} = 0.987 \)
Используя уравнение (4), \({K}_{e} \) равно 0.987.
Топографический фактор, \( {K}_{zt} \)
Параметры для расчета топографического фактора, \({K}_{zt}\), показаны на рисунке 26.8-1 ASCE 7-16. Чтобы определить, требуются ли дальнейшие расчеты топографического фактора, нам нужно проверить это, используя Section 26.8.1. Если сайт не соответствует всем перечисленным условиям, тогда топографический фактор можно принять за 1.0. Из высоты земли, созданной из высот Google, можно предположить, что местность Плоская, следовательно, \({K}_{zt}\) можно предположить, что 1.0 для ветра, дующего с юга.
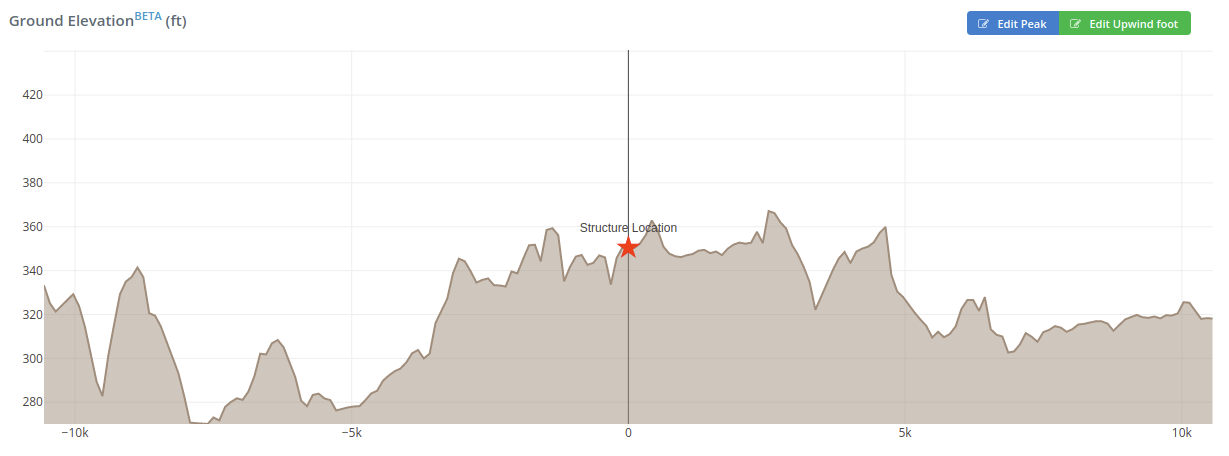
фигура 5. Профиль высоты площадки при направлении ветра Ю-С.
Коэффициент Давления Скорости, \({K}_{z}\)
Коэффициент скорости давления, \({K}_{z}\), можно рассчитать с помощью таблицы 26.10-1 ASCE 7-16. Этот параметр зависит от высоты над уровнем земли точки, где рассматривается давление ветра, и категория воздействия. более того, значения, указанные в таблице, основаны на следующей формуле:
Для 15 футов < \({z}\) < \({z}_{g}\): \({K}_{z} = 2.01(z/{z}_{g})^{2/α}\) (5)
Для \({с участием}\) < 15фут: \({K}_{z} = 2.01(15/{z}_{g})^{2/α}\) (6)
куда:
Стол 3. Значения α и \({z}_{g}\) из таблицы 26.11-1 ASCE 7-16.
| Контакт | а | \({z}_{g}\) (фут) |
|---|---|---|
| В | 7 | 1200 |
| С | 9.5 | 900 |
| D | 11.5 | 700 |
Для этого примера, мы будем учитывать высоту монтажа солнечной установки.
\({K}_{z} = 2.01((15)/(900))^{2/(9.5)} = 0.85 \)
\({K}_{z} = 0.85 \)
Скоростное давление
Из уравнения (3), мы можем решить для скорости давления, \( {q}_{h}\) в ПСФ, при монтажной высоте равной 8.33 фут.
\({q}_{h} = 0.00256{K}_{z}{K}_{zt}{K}_{d}{K}_{e}V^2\)
\({q}_{h} = 0.00256(0.85)(1.0)(0.85)(0.987)(100)^2 = 18.256 psf\)
\({q}_{h} = 18.256 psf\)
Для расчета расчетного ветрового давления, мы будем использовать уравнение (1). Подробная информация об этих параметрах показана ниже..
Фактор порыва, \(G\)
При определении коэффициента порыва ветра, \(G\), сначала нам нужно вычислить основную собственную частоту конструкции \( {n}_{1} \). Если \( {n}_{1} \) меньше чем 1 Гц, он будет классифицирован как гибкая структура, следовательно, нам нужно будет вычислить для \(G\) используя раздел 26.11.5. В этом примере, для упрощенного подхода, будем считать, что наша солнечная панель жесткая, где \(G\) равно 0.85 на основе раздела 26.11.1 ASCE 7-16. Следует отметить, что при определении коэффициента порыва ветра, особенно для гибких конструкций, требуется тщательная проверка основной собственной частоты конструкции, поскольку она увеличивает этот параметр..
Коэффициент полезного давления, \({C}_{N}\), Угол наклона ≤ 45°
Для определения коэффициентов чистого давления, \( {C}_{N} \), будем считать солнечную панель открытым зданием с односкатной крышей. Мы можем получить эти значения из рисунка 27.3-4 ASCE 7-16 с предположением “Чистый поток ветра.” Обратите внимание, что эти значения применимы только к солнечным панелям с углом наклона меньше или равным 45°.
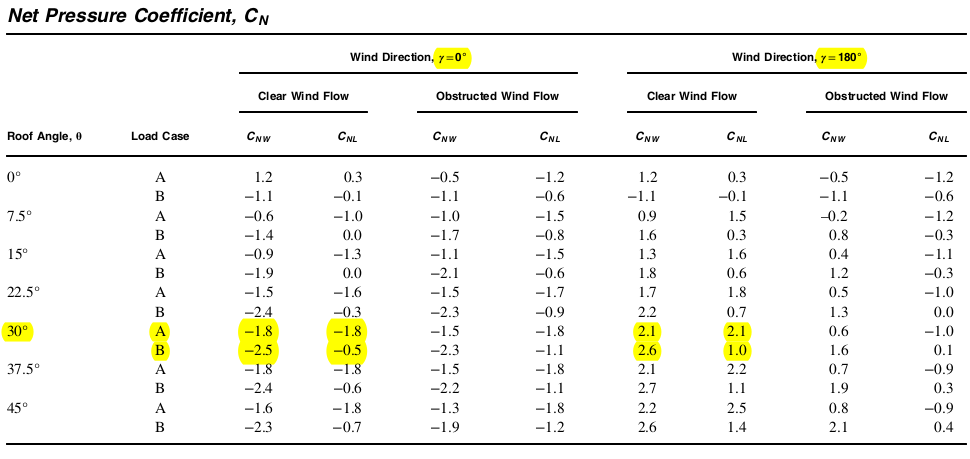
фигура 6. Коэффициент полезного давления, \( {C}_{N} \), значения из рисунка 27.3-4 ASCE 7-16 для открытого здания с односкатной крышей.
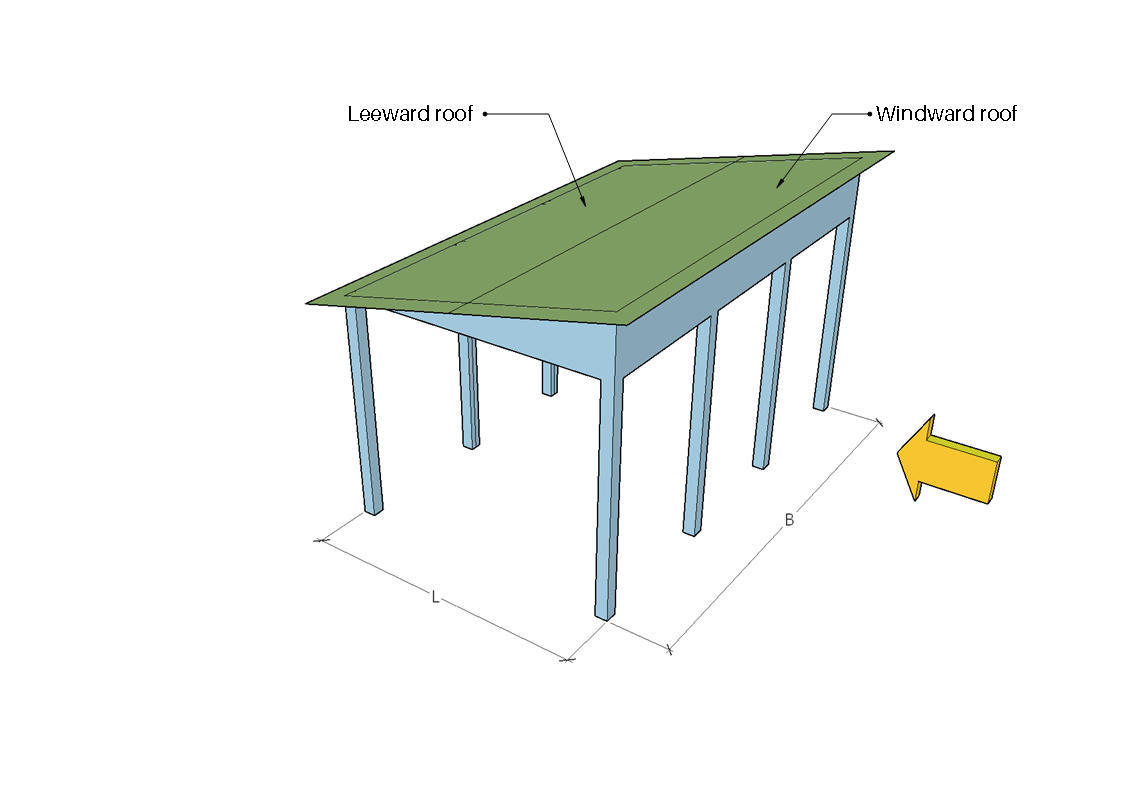
фигура 7. Наветренная и подветренная зоны для дирекционного угла, равного 0° .
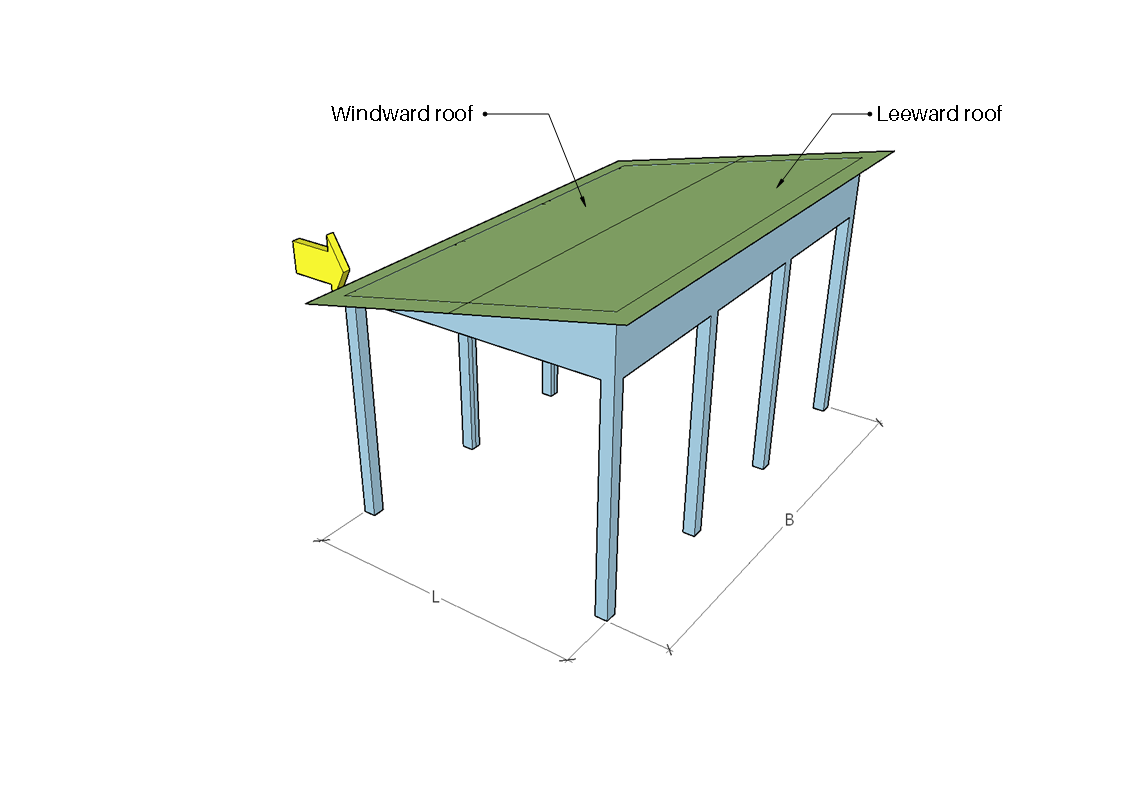
фигура 8. Наветренная и подветренная зоны для дирекционного угла, равного 180°.
Так как угол наклона солнечной панели равен 30°, соответствующие коэффициенты чистого давления, \( {C}_{N} \), использовать следующие:
Стол 4. Значения \( {C}_{N} \) для использования на основе рисунка 27.3-4 ASCE 7-16.
| Вариант нагрузки | Направление = 0° | Направление = 180° | ||
|---|---|---|---|---|
| \( {C}_{N,windward} \) | \( {C}_{N,leeward} \) | \( {C}_{N,windward} \) | \( {C}_{N,leeward} \) | |
| А | -1.8 | -1.8 | 2.1 | 2.1 |
| В | -2.5 | -0.5 | 2.6 | 1.0 |
Обратите внимание, что отрицательное значение означает, что давление ветра направлено от поверхности, а положительное значение означает, что давление ветра направлено к поверхности.. Из таблицы 4, можно сделать вывод, что мы рассмотрим четыре (4) Варианты нагрузки для ветровой нагрузки на нашу солнечную панель.
Расчетное давление ветра – Угол наклона ≤ 45°
При расчете ветровой нагрузки на солнечные батареи с учетом угла наклона > 45°, мы будем использовать уравнение (1), следовательно, ветровые нагрузки на наземные солнечные панели:
\({q}_{h} = 18.256 psf\)
\( G = 0.85\)
Стол 5. Расчетные ветровые нагрузки на наземные солнечные панели, применяемые к конструкции.
| Вариант нагрузки | Направление = 0° | Направление = 180° | ||
|---|---|---|---|---|
| наветренный, PSF |
подветренный, PSF | наветренный, PSF | подветренный, PSF | |
| А | -27.932 | -27.932 | 32.587 | 32.587 |
| В | -38.794 | -7.759 | 40.346 | 15.518 |
Следовательно, ветровые нагрузки на наземные солнечные панели при их применении следующие::
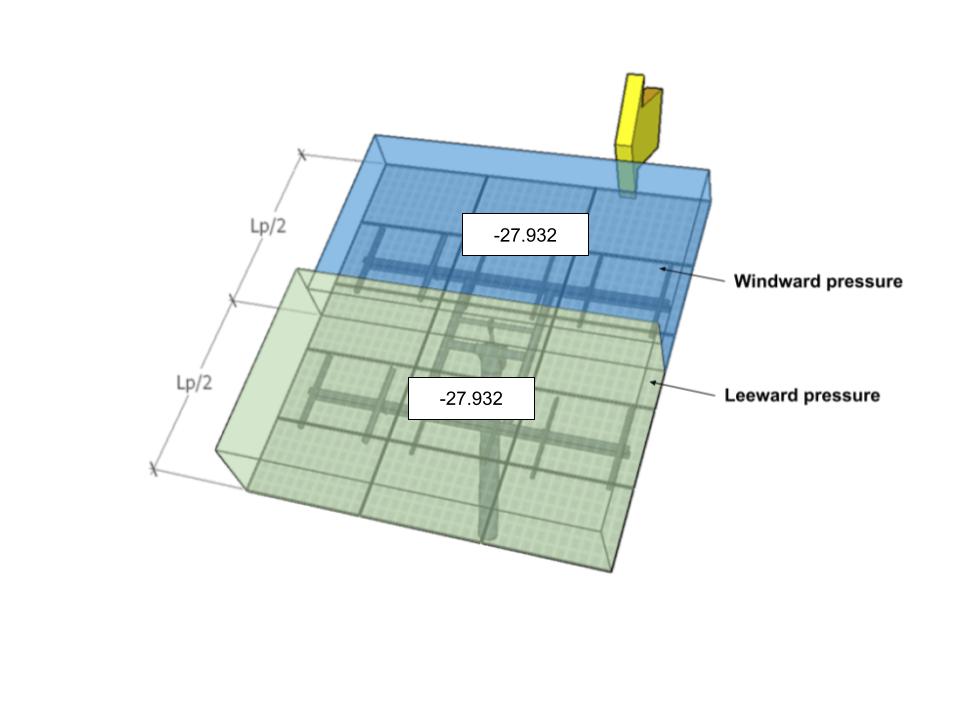
фигура 9. Расчетное давление ветра для угла направления 0° – Вариант нагрузки А.
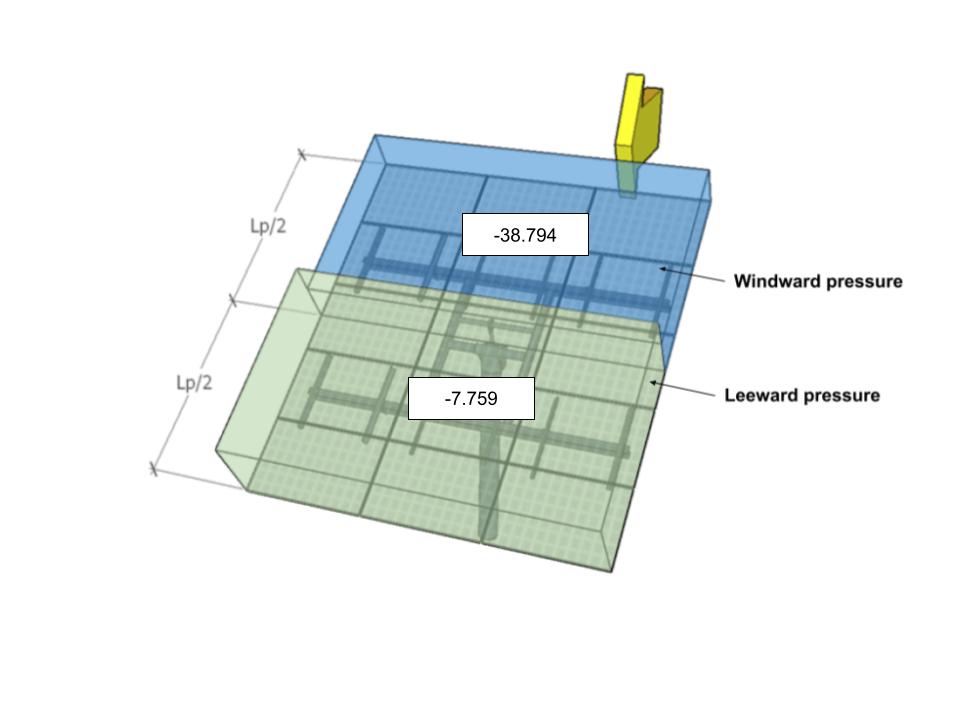
фигура 10. Расчетное давление ветра для угла направления 0° – Вариант нагрузки B.
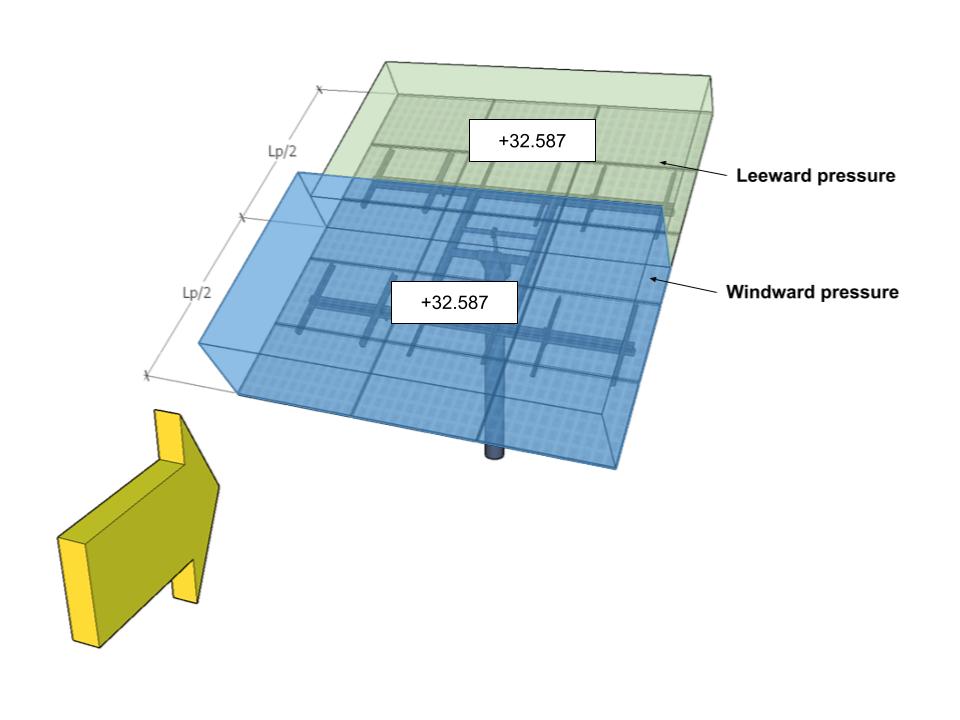
фигура 11. Расчетное давление ветра для угла направления 180° – Вариант нагрузки А.
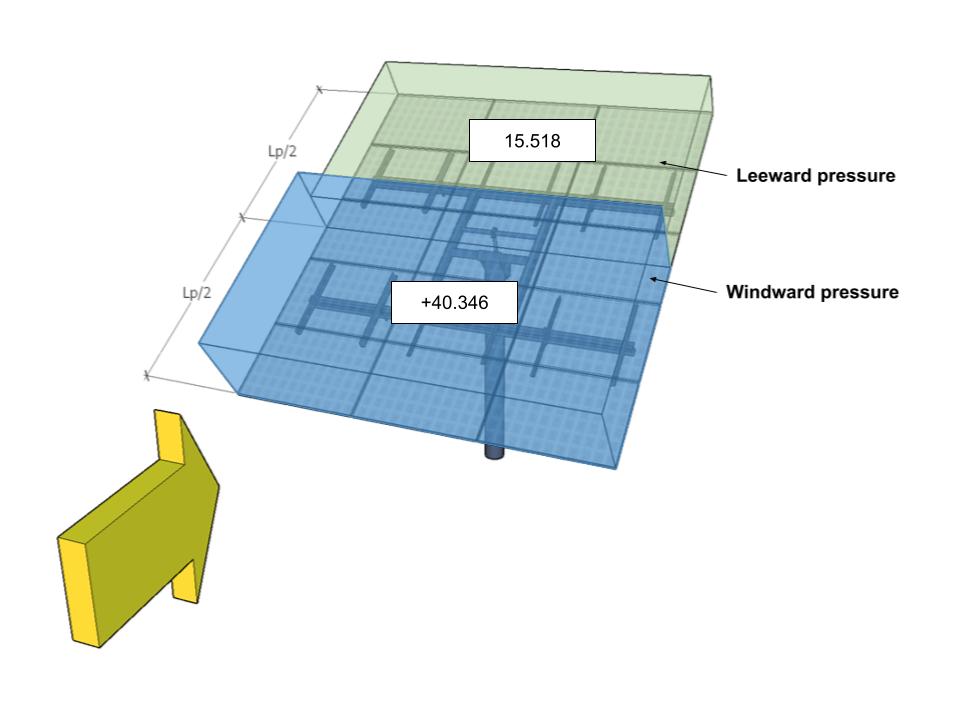
фигура 12. Расчетное давление ветра для угла направления 180° – Вариант нагрузки B.
Коэффициент чистой силы, \({C}_{f}\), – Размеры солнечной панели > 45°
Допустим, угол наклона нашей солнечной панели изменился на 60°. Нам нужно использовать вертикальную проекцию солнечной панели и рассматривать ее как сплошной знак со скоростным давлением, рассчитанным до вершины этой проекции..
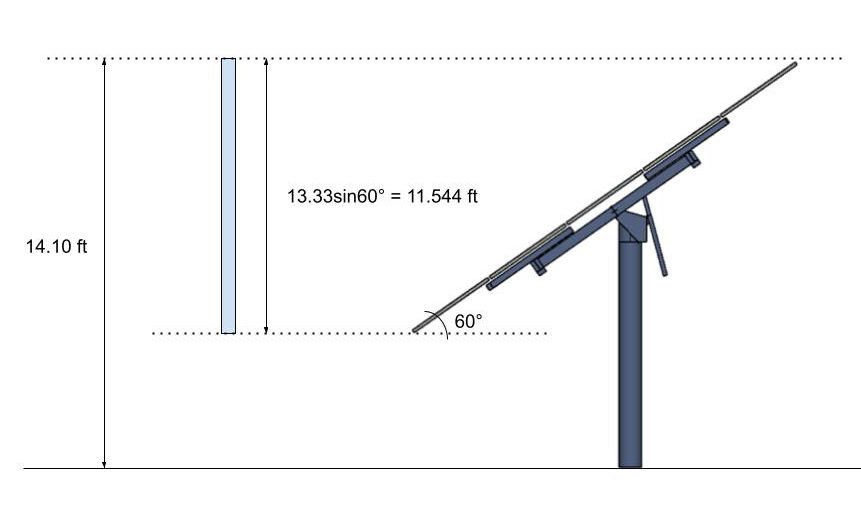
фигура 13. Вертикальную проекцию солнечной панели считать сплошным знаком.
Поскольку высота от земли до вершины проекта все же меньше 15 фут, мы все еще можем использовать наши расчетные \( {K}_{z}\) выше. следовательно, расчетное значение \( {q}_{h}\) все равно было бы то же самое. Сеть для коэффициента, \( {C}_{f}\), для использования можно получить из рисунка 29.3-1 ASCE 7-16. более того, при расчете этих силовых коэффициентов, мы будем рассматривать только случай A для упрощенного подхода. С рисунка 29.3-1:
\({q}_{h} = 18.256 psf\)
\( B = 16.25 ft\)
\( s = 11.544 ft\)
\( h = 14.102 ft\)
\( s/h = 0.818\)
\( B/s = 1.408\)
Из табличных значений \( {C}_{f} \) на рисунке 29.3-1, будем интерполировать известные значения \( B/s \) равно 1 и 2, и \( s/h \) равно 0.9 и 0.7.
фигура 14. Коэффициент полезной силы, \( {С}_{е} \), значения из рисунка 29.3-1 ASCE 7-16 для сплошных знаков.
Интерполируя выделенные значения, чтобы получить \( {C}_{f} \) от нашего \( B/s \) и \( s/h \), мы получили:
\( {C}_{f} = 1.5706 \)
Расчетное давление ветра – Размеры солнечной панели > 45°
При расчете ветровой нагрузки на солнечные батареи с учетом угла наклона > 45°, мы будем использовать уравнение (2), следовательно, ветровые нагрузки на наземные солнечные панели:
\({q}_{h} = 18.256 psf\)
\( G = 0.85\)
\( {C}_{f} = 1.5706 \)
\(p = {q}_{h}G{C}_{f} = (18.256)(0.85)(1.5706) = 24.372 psf\)
\(p = 24.372 psf\)
Следовательно, ветровые нагрузки на наземные солнечные панели при применении: 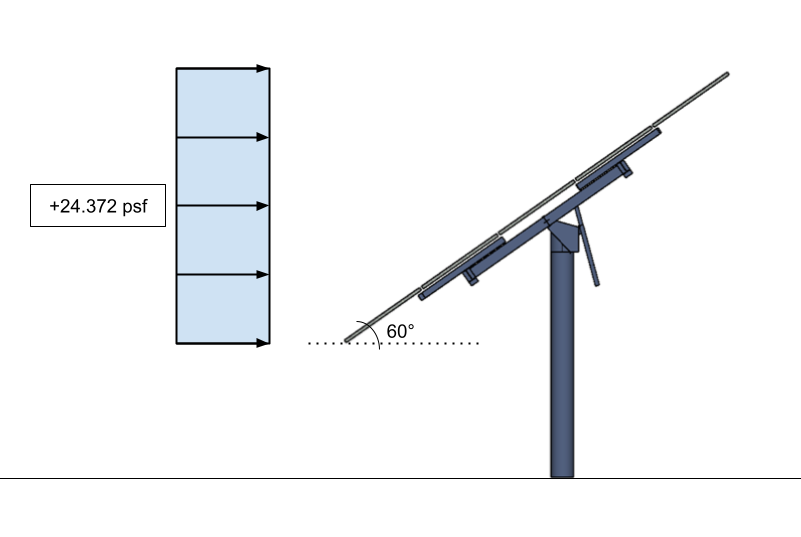
фигура 15. Расчетное давление ветра для солнечной панели в виде твердого знака – применяется к вертикальной проекции.
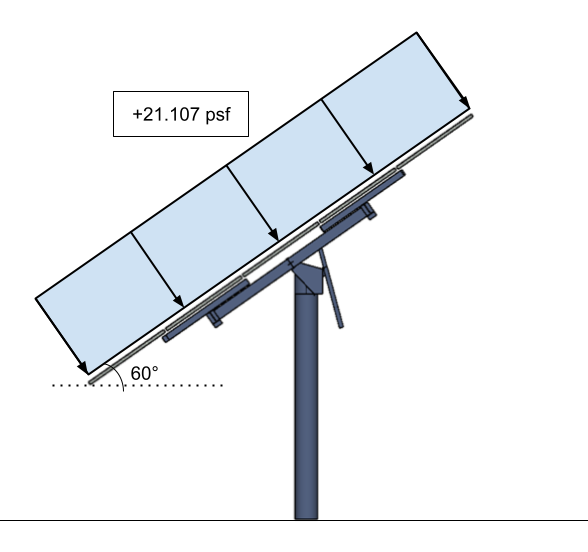
фигура 16. Преобразованное расчетное давление ветра для солнечной панели в виде твердого знака – наносится на поверхность солнечной панели.
Все расчеты ветра можно выполнить с помощью генератора нагрузки SkyCiv для ASCE. 7-16 (калькулятор ветровой нагрузки солнечной панели). Пользователи могут ввести местоположение сайта, чтобы получить данные о скорости ветра и местности., ввести параметры солнечной панели и сгенерировать расчетное давление ветра. С автономной версией, вы можете упростить этот процесс и получить подробный отчет о расчете ветровой нагрузки для солнечных батарей!
Снежная нагрузка
Для регионов со снегом, также следует учитывать снеговую нагрузку на солнечную панель. Рассчитать снеговую нагрузку для нашей солнечной батареи, мы будем использовать главу 7 ASCE 7-16. Мы будем рассматривать конструкцию солнечной панели как здание с односкатной крышей и мы будем рассматривать только сбалансированную снеговую нагрузку (снеговая нагрузка скатной крыши). Формулы для определения снеговой нагрузки для нашей солнечной панели следующие::
Расчет снеговой нагрузки на плоскую крышу \({p}_{f} \):
\({p}_{f} = 0.7{C}_{e}{C}_{t}{I}_{s}{p}_{g} \) (7)
куда:
\({C}_{e} \) = фактор воздействия
\({C}_{t} \) = тепловой фактор
\({I}_{s} \) = коэффициент важности для снеговой нагрузки
\({p}_{g} \) = снеговая нагрузка на грунт, в ПСФ
Рассчитать снеговую нагрузку скатной крыши \({p}_{s} \):
\({p}_{s} = {C}_{s}{p}_{f} + {p}_{r} \) (8)
куда:
\({C}_{s} \) = коэффициент уклона крыши
\({p}_{r} \) = дополнительная нагрузка в случае дождя и снега
Фактор воздействия, \({C}_{e} \)
Фактор экспозиции, \({C}_{e} \), можно определить из таблицы 7.3-1 ASCE 7-16 на основе шероховатости поверхности и экспозиции крыши. Со спутникового снимка местоположения, которое мы получили от Google Maps, мы можем классифицировать, что это место Шероховатость поверхности C (открытая местность с разбросанными препятствиями, высота которых обычно меньше 30 фут) и при условии, что солнечные панели полностью открытые и без препятствий. следовательно, в Фактор воздействия, \({C}_{e} \), структуры равно 0.9.
Термический фактор, \({C}_{t} \)
Термический фактор, \({C}_{t} \), можно определить из таблицы 7.3-2 ASCE 7-16 исходя из теплового состояния конструкции зимой. Из таблицы, мы можем классифицировать нашу солнечную панель как “Неотапливаемые и открытые конструкции.” Следовательно, соответствующий Термический фактор, \({C}_{t} \), для структуры равно 1.2.
Фактор важности снеговой нагрузки, \({I}_{s} \)
Фактор важности снеговой нагрузки, \({I}_{s} \), можно определить из таблицы 1.5-2 ASCE 7-16 на основе категории риска конструкции. Поскольку сооружение относится к категории риска I, из таблицы, \({I}_{s} \) равно 0.8.
Снеговая нагрузка на грунт, \({p}_{g} \)
Снеговая нагрузка на грунт, \({p}_{g} \), можно определить из рисунка 7.2-1 ASCE 7-16 как показано ниже. Из этой фигуры, в снеговая нагрузка на грунт, \({p}_{g} \) для нашей солнечной панели равно 10 PSF.
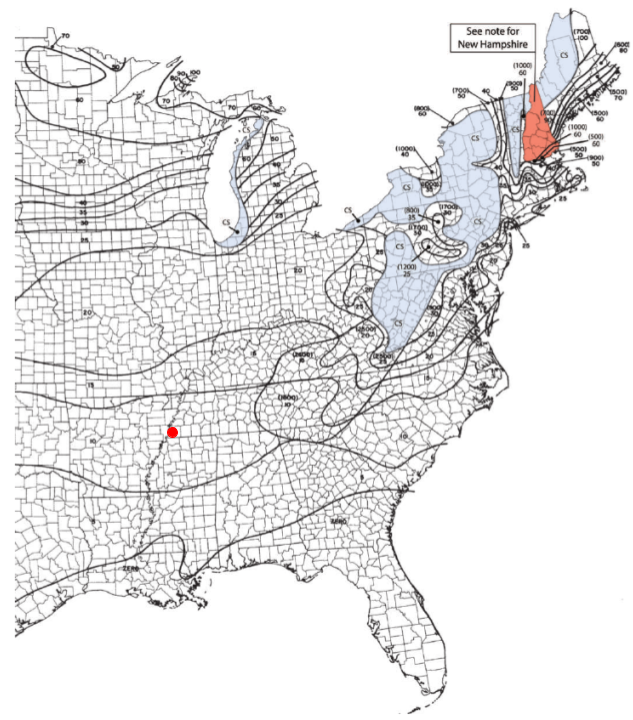
фигура 17. Карта снеговой нагрузки на грунт с рисунка 7.2-1 ASCE 7-16 с красной точкой, чтобы указать местоположение нашей солнечной панели.
SkyCiv также автоматизирует расчет снеговой нагрузки на грунт с помощью нескольких параметров.. Попробуйте наши Калькулятор ветровой нагрузки солнечной панели
Снеговая нагрузка на плоскую крышу, \({p}_{f} \)
Из параметров выше, мы уже можем рассчитать снеговую нагрузку на плоскую крышу, \({p}_{f} \), используя уравнение (7):
\({p}_{f} = 0.7{C}_{e}{C}_{t}{I}_{s}{p}_{g} \)
\({p}_{f} = 0.7(0.9)(1.2)(0.8)(10) = 6.048 psf \)
\({p}_{f} = 6.048 psf \)
Коэффициент уклона крыши, \({C}_{s} \)
Коэффициент уклона крыши можно рассчитать по рис. 7.4-1 ASCE 7-16 в зависимости от угла наклона, препятствие под поверхностью крыши, и значение теплового фактора \({C}_{t} \). Для нашей солнечной панели, будем считать, что наша солнечная панель классифицируется как “Скользкая поверхность.” Так как тепловой фактор \({C}_{t} \) равно 1.2, мы уже можем интерполировать значение \({C}_{s} \) с 7-2с. Из графика, известные значения:
\({C}_{s} = 1.0 \) for 15°
\({C}_{s} = 0.0 \) for 70°
Интерполируя эти значения, мы можем получить:
\({C}_{s} = 0.727 \) for 30°
Следовательно, \({C}_{s} = 0.727 \) для нашей солнечной панели.
Дождь на снегу Дополнительная нагрузка, \({p}_{r} \)
Дополнительный 5 PSF Дождь-на-снег надбавка нагрузка, \({p}_{r} \), следует рассматривать места, где \({p}_{g} \) меньше или равно 20 psf но не ноль, для всех крыш с углом наклона (в градусах) меньше, чем \( W/50 \) градусов, где \( W \) горизонтальное расстояние от карниза до конька. Значение \({p}_{r} \) относится только к скатной крыше (уравновешивается) загружение. Для этого примера:
\(W = 13.33 cos 30° = 11.544 ft \)
\( W/50 =0.231° \)
поскольку \({p}_{g} = 10 psf \) но угол наклона 30° больше, чем \( W/50 =0.231° \), \({p}_{r} \) можно пренебречь и равен 0.0
Снеговая нагрузка на наклонную крышу, \({p}_{s} \)
Из уравнения (8), мы можем рассчитать снеговую нагрузку скатной крыши \({p}_{s} \):
\({p}_{s} = {C}_{s}{p}_{f} + {p}_{r} \)
\({p}_{s} = (0.727)(6.048) + 0.0 = 4.397 psf \)
\({p}_{s} = 4.397 psf \)
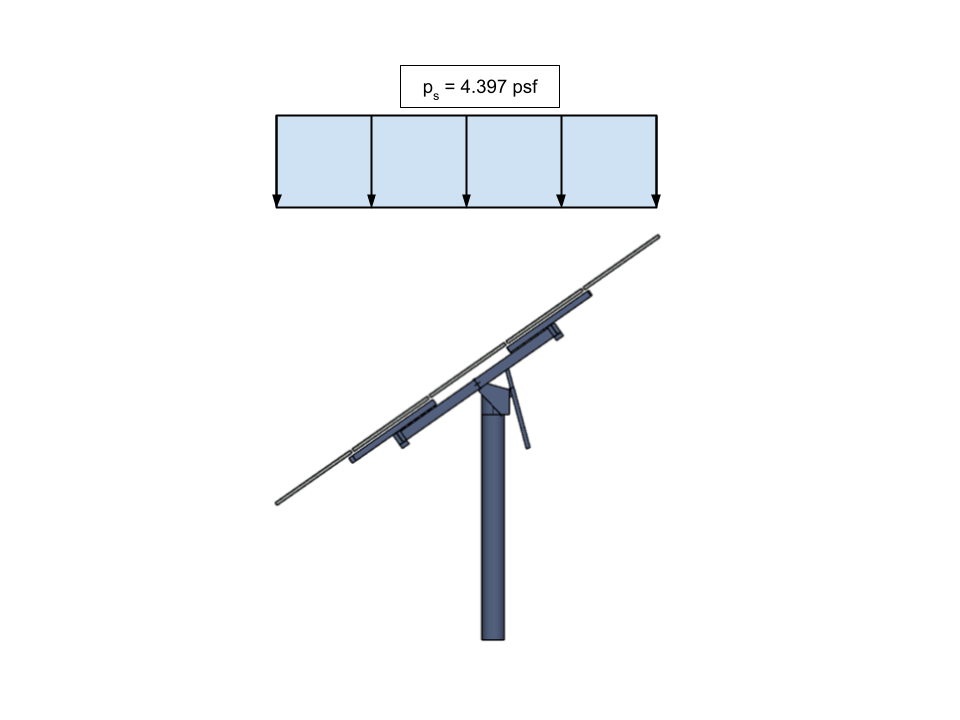
фигура 18. Расчетная сбалансированная снеговая нагрузка (снеговая нагрузка скатной крыши) для солнечной панели, нанесенной на горизонтальную проекцию конструкции.
Обратите внимание, что \({p}_{s} \) наносится на горизонтальную проекцию конструкции. Нам нужно будет преобразовать это значение в эквивалентную наклонную нагрузку от давления, чтобы мы могли применить его к нашей модели..
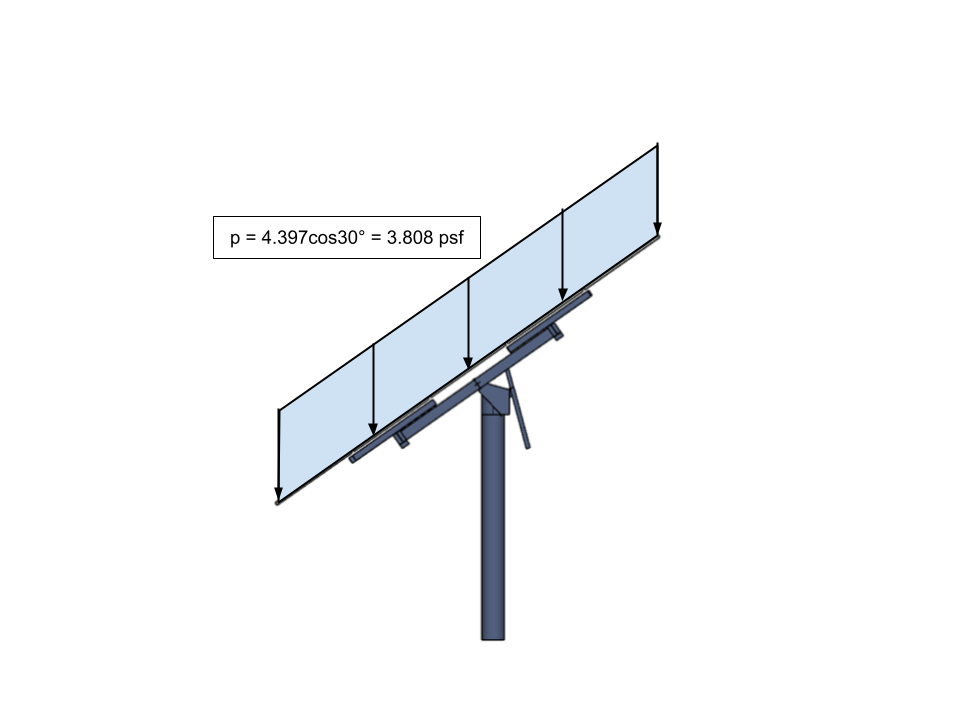
фигура 19. Преобразованная сбалансированная снеговая нагрузка (снеговая нагрузка скатной крыши) для солнечной панели, которая будет применена к нашей модели.
Расчеты снеговой нагрузки также можно выполнить в генераторе нагрузки SkyCiv для ASCE. 7-16. тем не мение, он доступен только в нашей автономной версии и профессиональной учетной записи..
Генератор нагрузки SkyCiv
варьируется в зависимости от высоты рассматриваемой высоты над землей, вы можете получить ветровые и снеговые нагрузки на наземные солнечные панели всего за несколько кликов и вводов. При покупке автономной версии или регистрации профессиональной учетной записи, вы сможете создать подробный отчет о расчетах ветра и снега для вашего проекта солнечной панели!
Вы можете проверить подробный отчет о ветровой и снеговой нагрузке на солнечную панель по этим ссылкам.:
более того, вы также можете создать свой собственный калькулятор ветровой нагрузки для солнечной панели, используя API SkyCiv Load Generator, точно так же, как мы создали решение для одного из наших клиентов.. Всего несколько входов, он автоматически спроектирует для вас систему солнечных батарей. Вы можете проверить нашу документацию по API через этот ссылка на сайт.
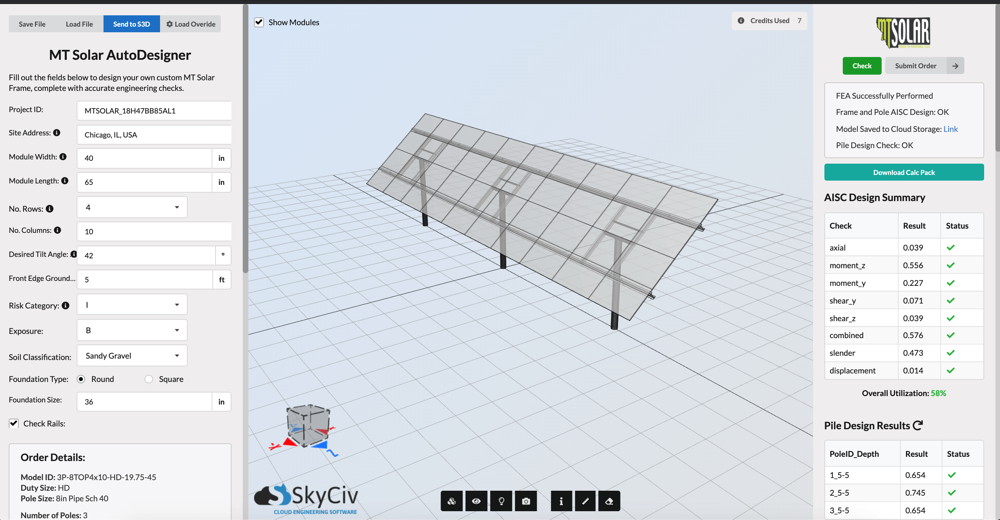
фигура 20. Наше индивидуальное решение для солнечной панели, созданное для MT Solar с использованием SkyCiv API.
Для дополнительных ресурсов, вы можете использовать эти ссылки:
- Введение в генератор нагрузки SkyCiv
- Ассе 7-16 Расчет ветровой нагрузки (Солнечные панели)
- Ассе 7 Расчет снеговой нагрузки
- Как рассчитать и применить нагрузку на снежный занос на крыше с ASCE 7-10
- Расчет снежных нагрузок на крышу с ASCE 7-10
Инженер-строитель, Разработка продукта
MS Гражданское строительство
Ссылки:
- Coulbourne, W. Л., & Стаффорд, T. Е. (2020, апрель). Ветровые нагрузки: Руководство по положениям ветровой нагрузки ASCE 7-16. Американское общество гражданских инженеров.
- Американское общество гражданских инженеров. (2017, июнь). Минимальные расчетные нагрузки и соответствующие критерии для зданий и других конструкций. Американское общество гражданских инженеров.
- = Расстояние с подветренной стороны от гребня до места, где перепад высот составляет половину высоты холма или откоса.
- MT Solar



