Полностью рабочий пример NBCC 2015 расчет снеговой нагрузки
Скопление снега на конструкциях может быть очень опасным для элементов крыши или других открытых элементов конструкции.. В Национальный строительный кодекс Канады (2015) Дивизион B – Раздел 4.1.6 обеспечивает подробный расчет снеговых нагрузок и связанных с ними дождевых нагрузок. Используя это руководство, мы продемонстрируем, как рассчитать снеговые нагрузки на примере Structural 3D (S3D) модель склада, как показано ниже:
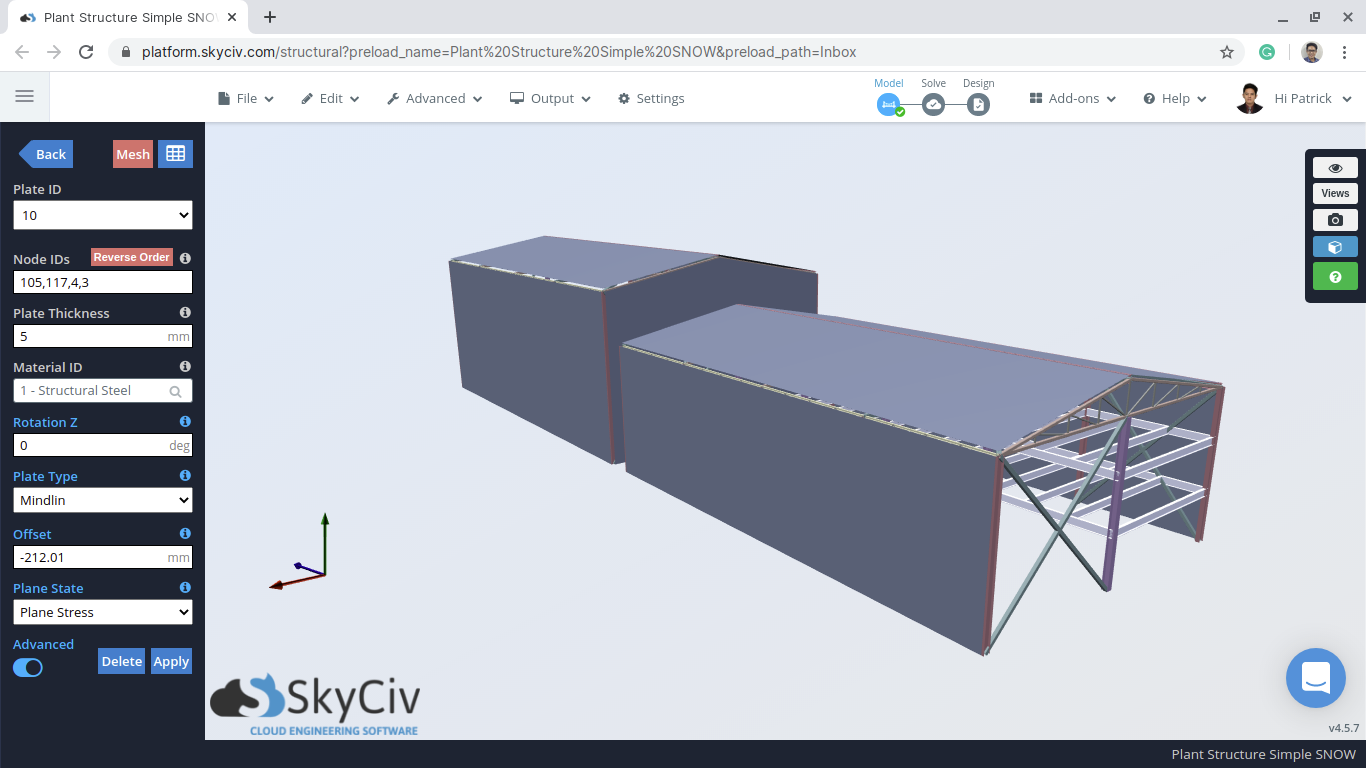
фигура 1: Пример модели склада S3D
фигура 2: Пример местоположения сайта с помощью Google Maps (только для иллюстрации).
Стол 1: Строительные данные, необходимые для расчета снеговой нагрузки.
| Расположение | Огден, Калгари, Альберта (только для иллюстрации) |
| Заполняемость | Склад или хранение материалов |
| Размеры | 19.508 м х 31.70 м для каждой конструкции Высота карниза меньшего здания 9.144 м Высота апекса меньшего здания 11.941 м Разница верхней и нижней кровли составляет 3.50 м Угол наклона крыши 16° |
| дополнительные детали | Крыша имеет скользкую поверхность Промежуток между конструкциями составляет 2.30 м |
Из таблицы 1, заданная снеговая нагрузка, \(S ), можно рассчитать по формуле:
\(S = {я}_{s}[{S}_{s}{С}_{б}{С}_{вес}{С}_{s}{С}_{а } +{S}_{р}]\) (1)
куда:
\({я}_{s}\) = коэффициент важности для снеговой нагрузки, Таблица 4.1.6.2-A
\({S}_{s}\) знак равно 1-через 50 лет снеговая нагрузка на грунт, кПа, Подраздел 1.1.3
\({С}_{б}\) = базовый коэффициент снеговой нагрузки на крышу, 4.1.6.2 (2)
\({С}_{вес}\) = коэффициент воздействия ветра на основе, 4.1.6.2 (3) и (4)
\({С}_{s}\) = коэффициент наклона, 4.1.6.2 (5), (6), и (7)
\({С}_{а }\) = коэффициент накопления, 4.1.6.2 (8)
\({S}_{р}\) = Связанная дождевая нагрузка 1 из 50 лет, кПа, Подраздел 1.1.3, но не больше чем \({S}_{s}{С}_{б}{С}_{вес}{С}_{s}{С}_{а }\)
Каждый параметр будет рассмотрен индивидуально в следующих разделах.. Будут рассчитаны следующие случаи снеговой нагрузки: сбалансированная и несбалансированная снеговая нагрузка на каждую крышу (ветер нормальный к гребню), а также снос, образующийся на нижней крыше с учетом накопления от скольжения.
Фактор важности, \({я}_{s}\)
Первое, что определяется, - это фактор важности, \({я}_{s}\), который находится с использованием Таблица 4.1.6.2-A как указано. Так как конструкция представляет собой складское здание, которое в случае поломки практически не повлияет на человеческую жизнь., категория важности Низкий. более того, расчет будет в предельном состоянии Ultimate (ULS). Так что из Таблица 4.1.6.2-A, \({я}_{s}\) равно 0.80.
| Категория важности | Фактор важности, \({я}_{s}\) | |
|---|---|---|
| ULS | СЛС | |
| Низкий | 0.8 | 0.9 |
| Обычный | 1.0 | 0.9 |
| Высокая | 1.15 | 0.9 |
| После катастрофы | 1.25 | 0.9 |
Снеговая нагрузка на грунт, \({S}_{s}\), и сопутствующая дождевая нагрузка, \(({S}_{р})\)
Снеговая нагрузка на землю, \({S}_{s}\), и сопутствующая дождевая нагрузка, \(({S}_{р})\), значения приведены в таблице Приложение C, Дивизион B NBCC 2015 в зависимости от местоположения и провинции. Для этого примера, соответствующий \({S}_{s}\) и \(({S}_{р})\) в Калгари Альберта равно 1.10 кПа и 0.1 кПа, соответственно.
Трудно найти снег на земле и связанную с ним дождевую нагрузку для NBCC 2015? Пытаться в Инструмент генератора свободной нагрузки SkyCiv чтобы ускорить поиск и получить соответствующий \({S}_{s}\) и \({S}_{р}\) в зависимости от расположения вашей конструкции.
Фактор воздействия ветра, \({С}_{вес}\)
Для фактора воздействия ветра, \({С}_{вес}\), разрешается быть равным 1.0 на основе 4.1.6.2 (3). Этот коэффициент все еще может быть уменьшен до тех пор, пока условия в 4.1.6.2 (4) доволен. Для этого примера, \({С}_{вес}\) должен быть равен 1.0 поскольку локация не является открытой местностью, полностью открывающей доступ к конструкции ветру.
Базовый коэффициент снеговой нагрузки на крышу, \({С}_{б}\)
Базовый коэффициент снеговой нагрузки на крышу, \({С}_{б}\), можно рассчитать по следующим формулам, как указано в 4.1.6.2 (2):
\({С}_{б} знак равно 0.8\) (2) для \({L}_{с} ≤ (70/{{С}_{вес}}^{2})\) и
\({С}_{б} знак равно (1/{С}_{вес}) [1 – (1 – 0.8{С}_{вес})exp(-0.01({L}_{с}{{С}_{вес}}^{2} – 70))] \) (3) для \({L}_{с} > (70/{{С}_{вес}}^{2})\)
куда:
\({L}_{с}\) = характерная длина верхней или нижней крыши, определяемая как: \(2вес -{вес}^{2}/л )
\(л ) = больший размер крыши в плане
\(w\) = меньший размер крыши в плане
Для этого примера,\(л ) и \(w\) равно 31.7 м и 19.51 м, соответственно, следовательно, \({L}_{с}\) равно 27.01. поскольку \({L}_{с}\) меньше чем \((70/{1.0}^{2})\), базовый коэффициент снеговой нагрузки крыши, \({С}_{б}\), равно 0.8.
Коэффициент наклона, \({С}_{s}\)
Расчет коэффициента наклона \({С}_{s}\) подробно в 4.1.6.2 (5), (6), и (7) показано ниже.
Для беспрепятственной скользкой крыши:
\({С}_{s} знак равно 1.0\) для \(α ≤ 15 ° )
\({С}_{s} знак равно 0\) для \(а > 60°\)
\({С}_{s} знак равно (60° – а )/45°\) для \(15° < α ≤ 60°\)
Для других случаев:
\({С}_{s} знак равно 1.0\) для \(α ≤ 30°\)
\({С}_{s} знак равно 0\) для \(а > 70°\)
\({С}_{s} знак равно (70° – а )/40°\) для \(30° < α ≤ 70°\)
Удельный вес снега, \(γ\)
Удельный вес снега указан в 4.1.6.13 и принимается как:
\(γ = 0.43{S}_{s} + 2.2 кН /{м}^{3} ≤ 4,0 кН /{м}^{3}\) (4)
Для этого примера, \(γ\) равно \(2.673 кН /{м}^{3}\).
Фактор накопления, \({С}_{а }\)
Фактор накопления, \({С}_{а }\), рассчитывается в зависимости от случая нагрузки рассматривается как подробно описанный в 4.1.6.2 (8). Это значение будет рассчитываться подробно для каждого случая..
Указанная снеговая нагрузка, \(S )
В этой секции, нормативная снеговая нагрузка, \(S ), будет рассчитан для сбалансированного и смещенного случаев.
Сбалансированный / нерасположенный корпус
Для сбалансированного / нерасположенного корпуса, в коэффициент накопления \({С}_{а }\) равно 1.0. более того, так как угол наклона крыши \(α\) является \(16°\) и поверхность крыши предполагается беспрепятственной скользкой, коэффициент наклона, \({С}_{s}\), для нашего примера равно 0.978. Используя уравнение (1), заданная снеговая нагрузка, \(S ), для сбалансированного / нерасположенного корпуса:
\(S = 0.8((1.10)(0.8)(1.0)(0.978)(1.0) +0.1)\) знак равно 0.769 кПа
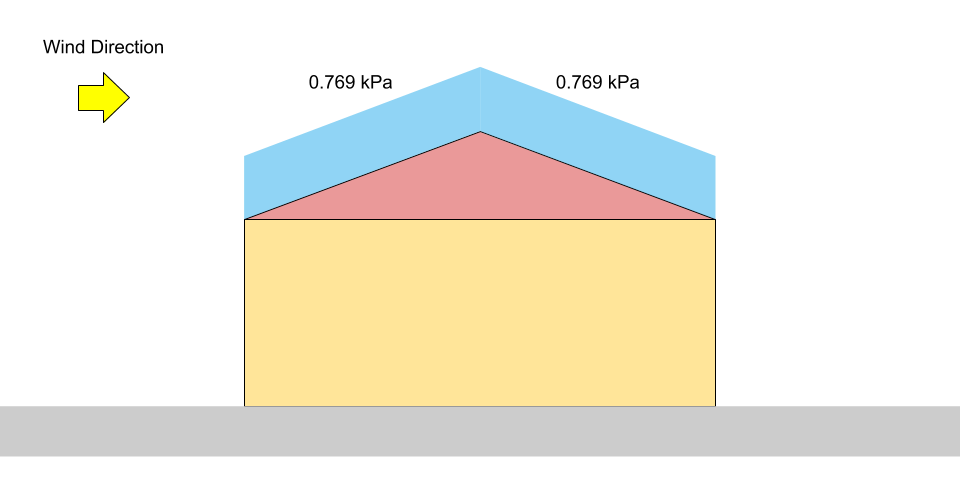
фигура 3: Диаграмма нагрузки для сбалансированной снеговой нагрузки на двускатную крышу.
Несбалансированный / дрейфующий корпус
Ветер, действующий перпендикулярно хребту
Поскольку конструкции имеют двускатную крышу, неуравновешенная снеговая нагрузка (ветер, действующий нормально к гребню) коэффициент накопления \({С}_{а }\) находится с использованием 4.1.6.9:
\({С}_{а , против ветра} знак равно 0\)
\({С}_{а , подветренный} знак равно 0.25 +α/20\) для \(15° ≤ α ≤ 20 ° )
\({С}_{а , подветренный} знак равно 1.25\) для \(20° < α ≤ 90°\)
Поскольку обе конструкции имеют угол наклона кровли равный 16 °., факторы накопления \({С}_{а , против ветра}\) и \({С}_{а , подветренный}\) равны 0 и 1.05, соответственно. более того, так как угол наклона крыши \(α\) является \(16°\) и поверхность крыши предполагается беспрепятственной скользкой, коэффициент наклона, \({С}_{s}\), для нашего примера равно 0.978.
В несбалансированном / заносном корпусе перпендикулярно гребню, \({С}_{а }\) рассчитывается на основе 4.1.6.9 для двускатной крыши. Из расчета выше, \({С}_{а , против ветра} знак равно 0\) и \({С}_{а , подветренный} знак равно 1.05\). следовательно, указанные снеговые нагрузки для каждой стороны:
\({S}_{против ветра} знак равно 0.8((1.10)(0.8)(1.0)(0.978)(0) +0.1)\) знак равно 0.08 кПа знак равно \({п}_{1}\)
\({S}_{подветренный} знак равно 0.8((1.10)(0.8)(1.0)(0.978)(1.05) +0.1)\) знак равно 0.803 кПа знак равно \({п}_{2}\)
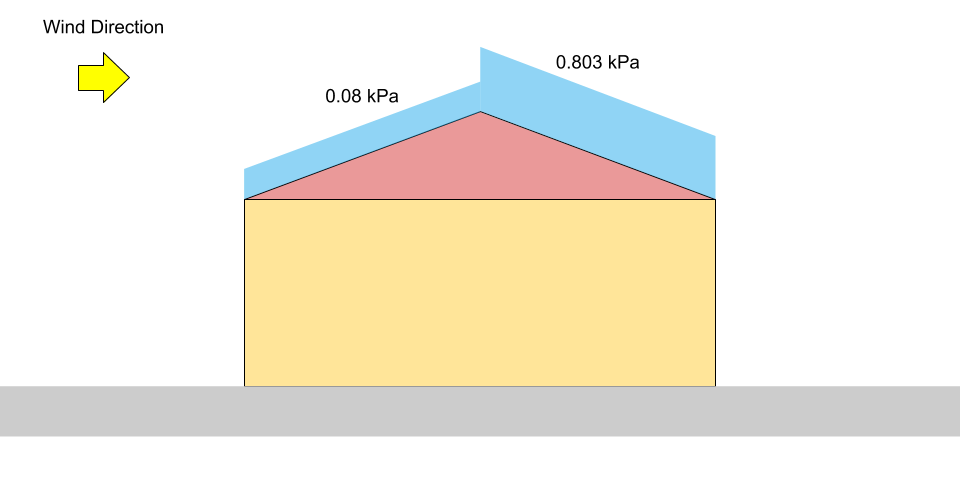
фигура 4: Диаграмма нагрузки при неуравновешенной снеговой нагрузке на двускатную крышу (не в масштабе).
Ветер, действующий параллельно хребту – Случай I – Ветер от верхней части крыши к нижней
Когда ветер дует параллельно гребню, на нижней крыше скорее всего будет образовываться сугроб. Для того, чтобы определить коэффициент накопления \({С}_{а }\), следующие формулы из 4.1.6.2 (8) используются:
\({С}_{а } знак равно{С}_{а0} – ({С}_{а0} – 1)(Икс/{Икс}_{d})\) для \(0 ≤ х ≤ {Икс}_{d}\)
\({С}_{а } знак равно 1.0\) для \(Икс > {Икс}_{d}\)
куда:
\({С}_{а0}\) = пиковое значение \({С}_{а0}\) при x = 0
\(Икс) = расстояние от ступеньки крыши
\({Икс}_{d}\) = длина выколотки, как показано на рисунке 3 ниже
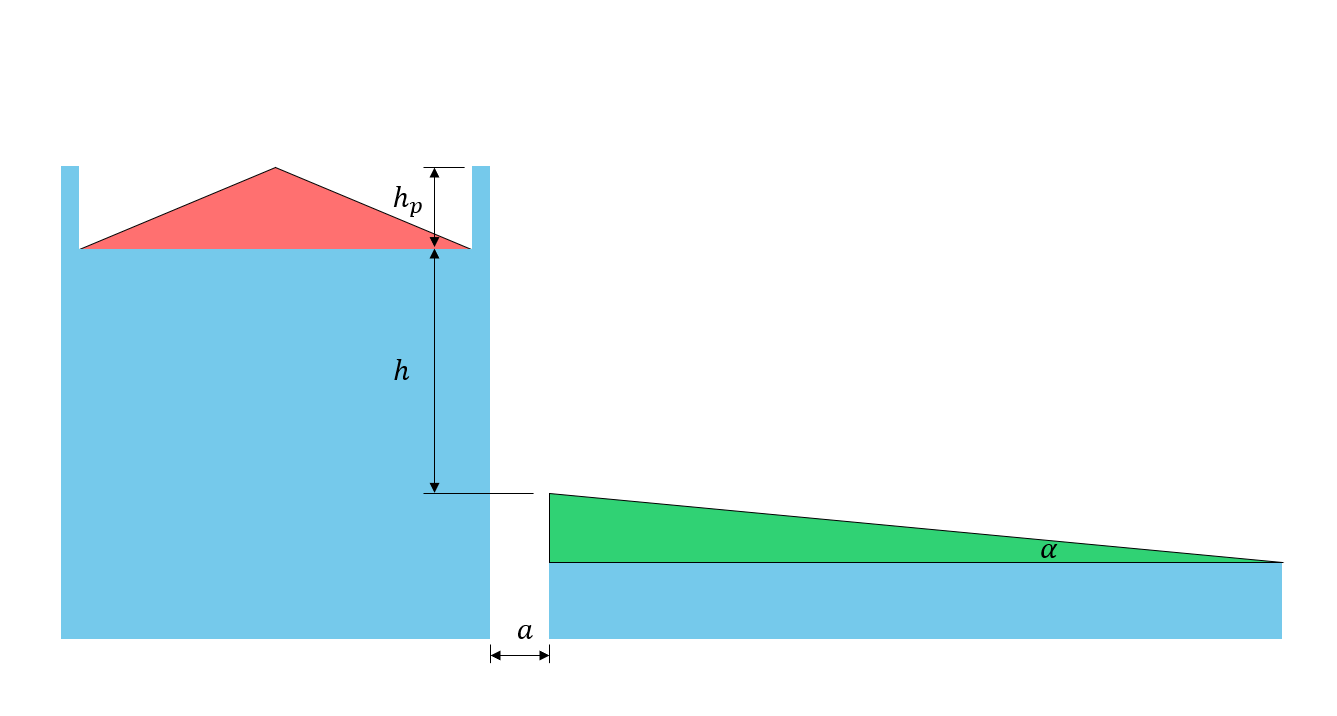
фигура 5: Иллюстрация параметров размеров крыши
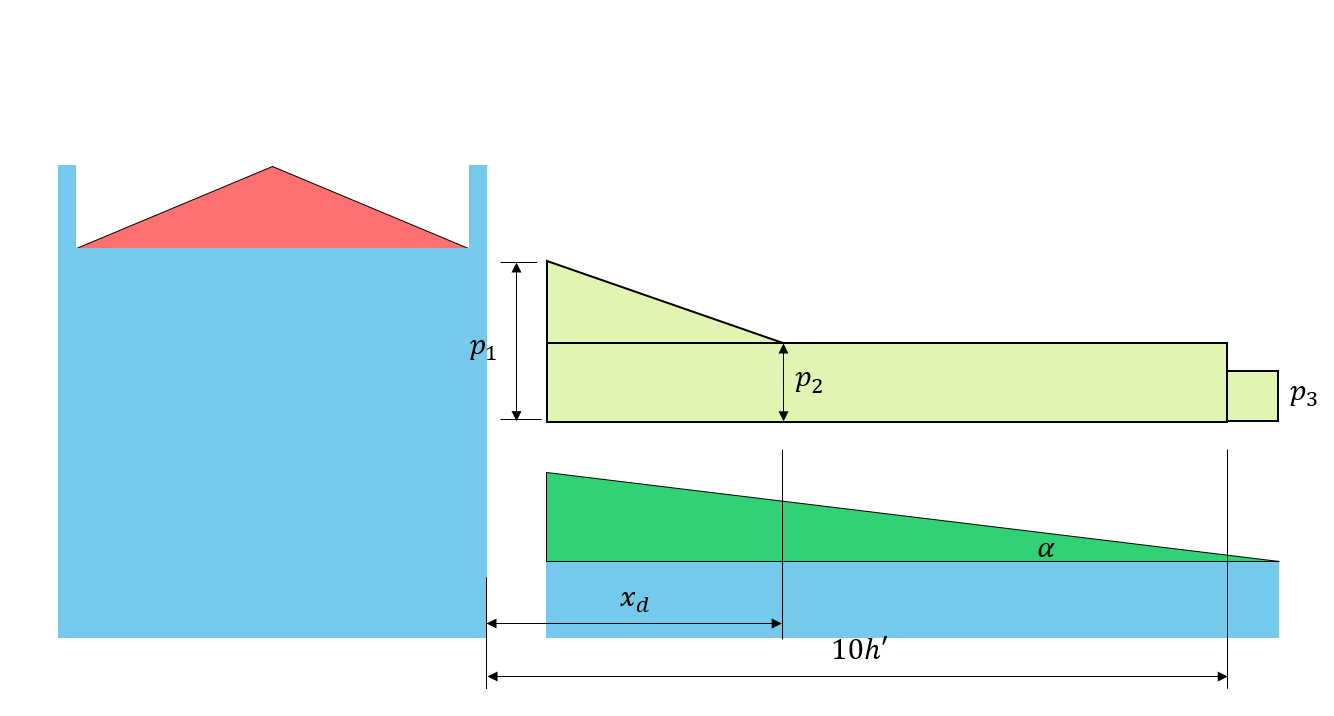
фигура 6: Соответствующая нагрузка заноса на нижнюю крышу на основе Рисунок 4.1.6.5-A.
\({С}_{а0}\) и \({Икс}_{d}\) можно рассчитать по следующим формулам:
\({С}_{а0} = frac{βγh}{{С}_{б}{S}_{s}}\) или \({С}_{а0} = frac{F}{{С}_{б}}\) (5), в зависимости от того, что меньше
\({Икс}_{d} знак равно 5 \гидроразрыва{{С}_{б}{S}_{s}}{с}({С}_{а0} – 1)\) (6)
\(F = 0.35β\sqrt{\гидроразрыва{с({L}_{cs} – 5{{час}_{п}}^{‘})}{{S}_{s}}} +{С}_{б}\) но \(F ≤ 5\) для \({С}_{WS} знак равно 1.0\) (7)
\({час}^{‘} = ч – \гидроразрыва{{С}_{б}{С}_{вес}{S}_{s}}{с}\) (8)
\({{час}_{п}}^{‘} знак равно{час}_{п} – \гидроразрыва{0.8{S}_{s}}{с}\) но \(0 ≤ {{час}_{п}}^{‘} ≤ \frac{{L}_{cs}}{5}\) (9)
куда:
\({час}_{п}\) = высота парапета на верхней крыше (0 в этом случае из-за отсутствия парапета)
\(час) = разница в высоте между верхним и нижним уровнем крыши
\({С}_{WS}\) = значение \({С}_{вес}\) применимо к источнику дрейфа
\({L}_{cs}\) = характерная длина области источника, определяемая как: \(2{вес}_{s} -{{вес}_{s}}^{2}/{L}_{s}\)
\({L}_{s}\) = больший размер в плане исходной области, как показано на рисунке 7 и 8, показано ниже
\({вес}_{s}\) = меньший размер в плане исходной области, как показано на рисунке 7 и 8, показано ниже
\(β ) знак равно 1.0 для случая I, и 0.67 для случаев II и III.
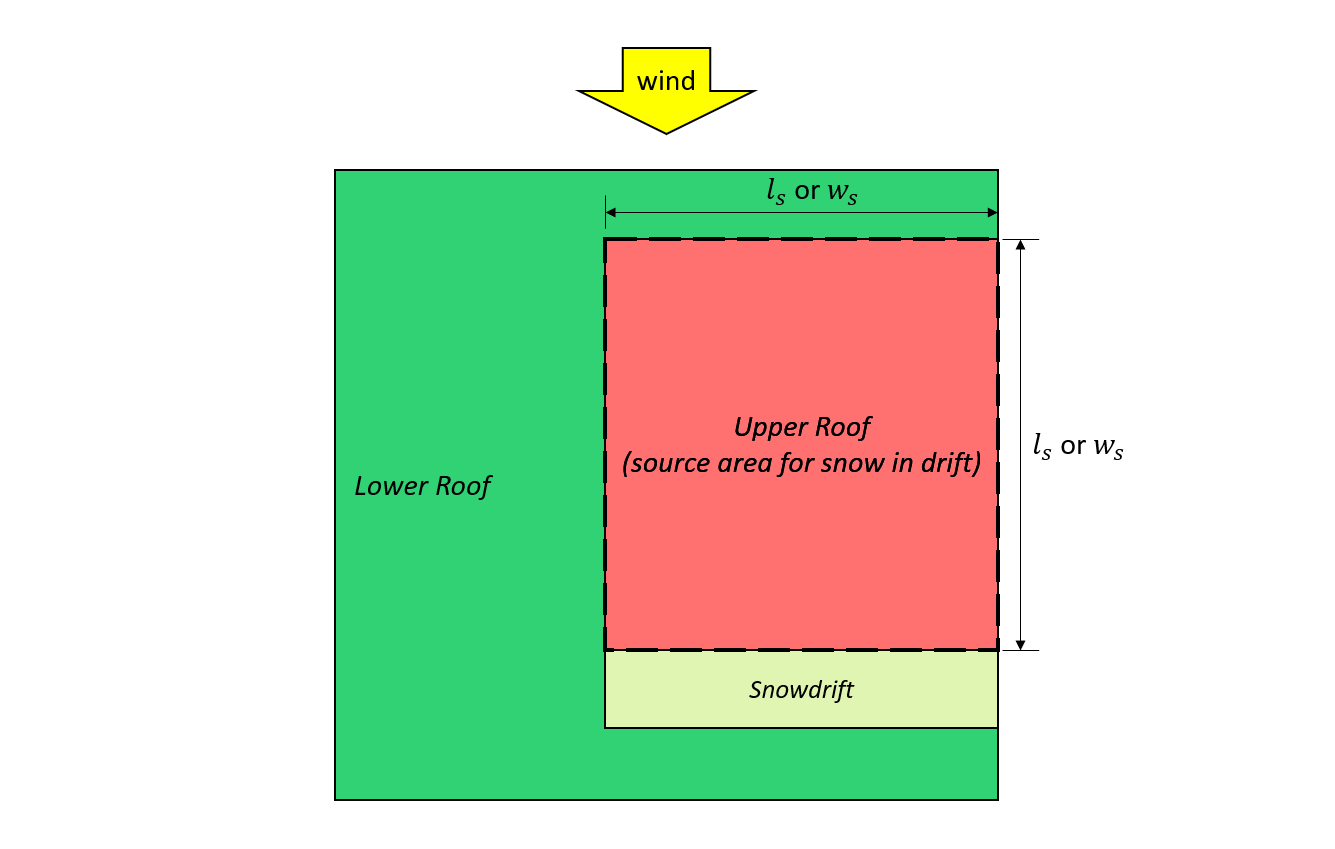
фигура 7: Случай I – сугроб, образованный ветром с верхней кровли на основе Рисунок 4.1.6.5-B.
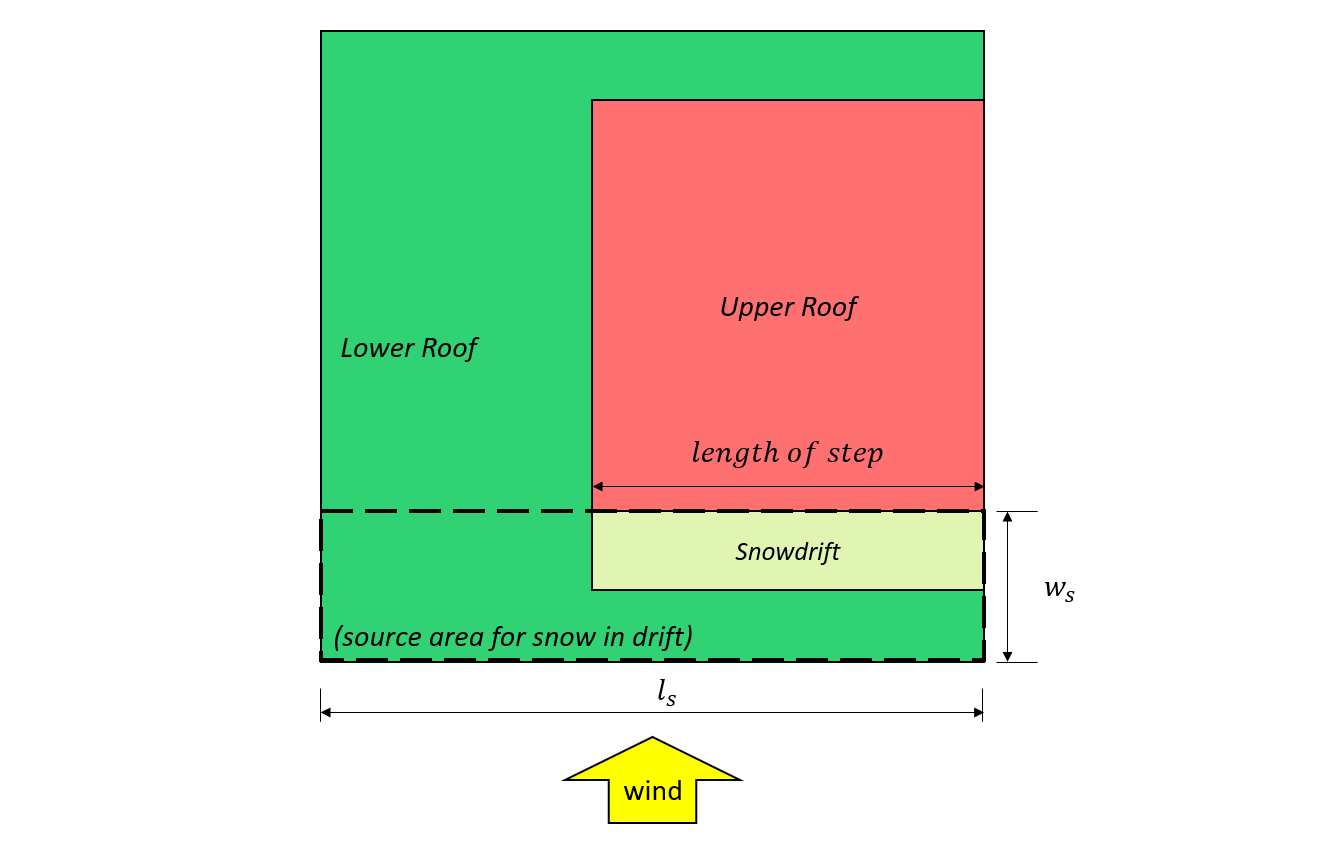
фигура 8: Дело II – сугроб, образовавшийся от ветра, идущего от нижней кровли на основании Рисунок 4.1.6.5-B.
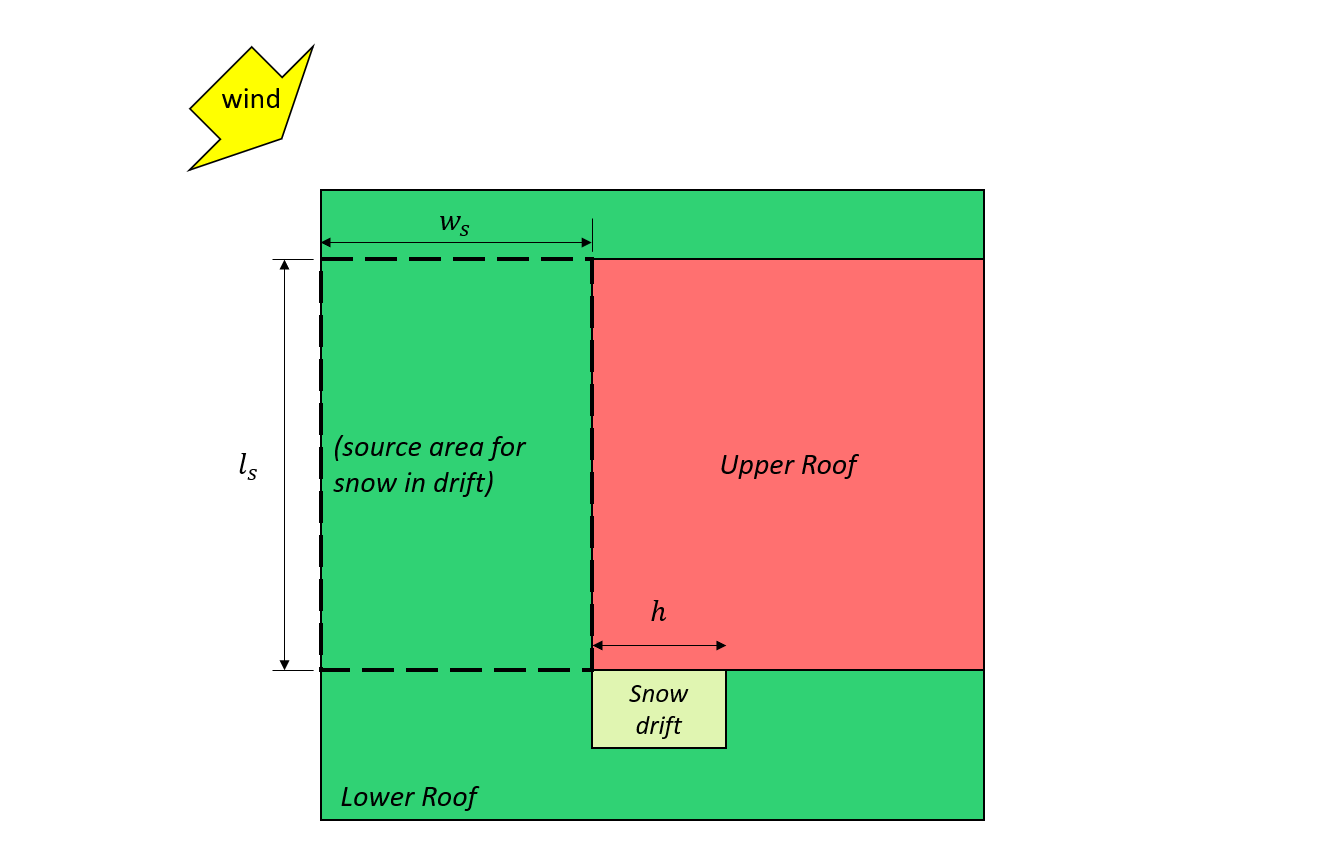
фигура 7: Дело III – частичный сугроб, образованный ветром с нижней кровли на основе Рисунок 4.1.6.5-B.
Для этого примера, Случаи I и II будут рассмотрены..
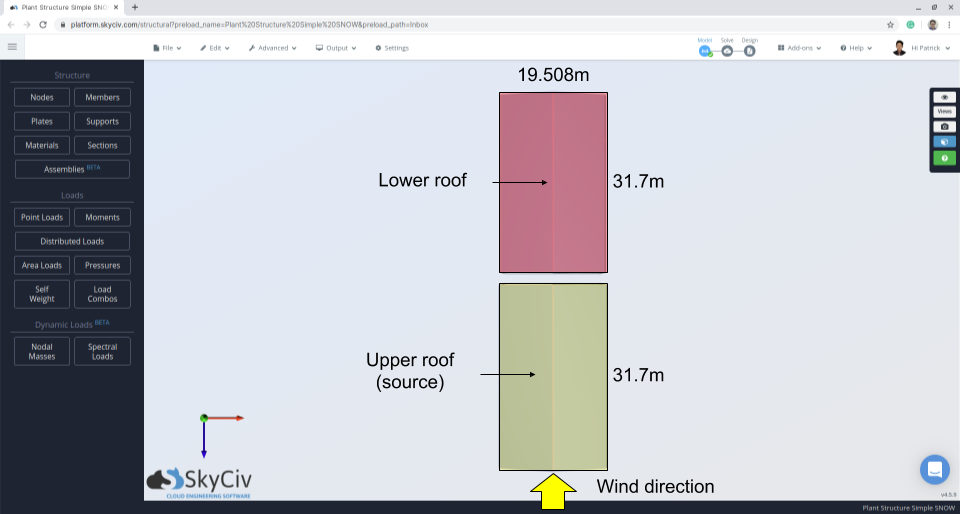
фигура 10: План конструкции с указанием направления ветра и области источника.
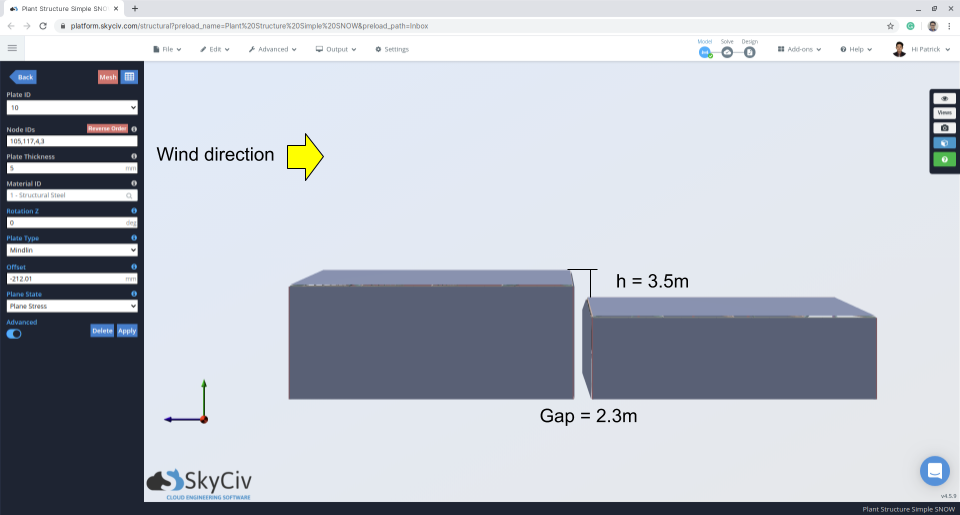
фигура 11: Вертикальный вид с указанием зазора и разницы между верхней и нижней крышей.
Для неуравновешенного / смещенного корпуса параллельно гребню, \({С}_{а }\) рассчитывается для случая I и случая II на основе 4.1.6.5 для многоуровневой кровли. Для случая I, следующие параметры должны быть сначала рассчитаны с использованием различных уравнений, ранее упомянутых в этом примере.:
\(β = 1.0\)
\({час}^{‘} знак равно (3.5) – \гидроразрыва{(0.8)(1.0)(1.10)}{(2.673)} знак равно 3.17 м )
\({час}_{п} знак равно 0\)
\({{час}_{п}}^{‘} =0\)
\({L}_{cs} знак равно 2(19.507) -{(19.507)}^{2}/(31.7) знак равно 27.01 м )
\(F = 0.35(1.0)\SQRT{\гидроразрыва{(2.673)((27.01) – 5(0))}{(1.10)}} +(0.8) знак равно 3.636\)
\({С}_{а0} = frac{(1.0)(2.673)(3.5)}{(0.8)(1.10)} знак равно 10.631\) или \({С}_{а0} = frac{3.66}{0.8} знак равно 4.544\)
\({С}_{а0} знак равно 4.544\)
\({Икс}_{d} знак равно 5 \гидроразрыва{(0.8)(1.10)}{2.673}(4.544 – 1) знак равно 5.835 м )
По этим параметрам, коэффициент накопления, \({С}_{а }\), можно рассчитать, подставив значение \({С}_{а0}\) на каждом \(Икс) расстояние. Обратите внимание, что нам нужно рассчитать \({С}_{а }\) в \(x = a\) где \(а ) это зазор между кровлей, поскольку зазор в крыше меньше, чем 5 м, как указано в 4.1.6.6.
в \(х = 0\): \({С}_{а } = 4,544 – (4.544 – 1)(0/5.835) знак равно 4.544\)
в \(x = a\): \({С}_{а } = 4,544 – (4.544 – 1)(2.3/5.835) знак равно 3.147\)
в \(х = {Икс}_{d}\): \({С}_{а } =1.0\)
в \(х = 10{час}^{‘}\): \({С}_{а } =1.0\)
Поскольку угол крыши для этого случая равен 0° по ссылке в этом разделе, \({С}_{s} знак равно 1.0\). более того, при нахождении заданной снеговой нагрузки на верхнюю кровлю, коэффициент накопления, \({С}_{а }\), и коэффициент наклона, \({С}_{s}\), оба равны 1.0. следовательно, величина указанных снеговых нагрузок в каждом месте составляет:
в \(х = 0\): \(S = 0,8((1.10)(0.8)(1.0)(1.0)(4.544) +0.1) знак равно 3.279 kPa\)
в \(x = a\): \(S = 0,8((1.10)(0.8)(1.0)(1.0)(3.147) +0.1) знак равно 2.295 кПа = {п}_{1}\)
в \(х = {Икс}_{d}\): \(S = 0,8((1.10)(0.8)(1.0)(1.0)(1.0) +0.1) знак равно 0.784 кПа ={п}_{2} знак равно {п}_{3}\)
на верхнем уровне крыши: \(S = 0,8((1.10)(0.8)(1.0)(1.0)(1.0) +0.1) знак равно 0.784 kPa\)
Ветер, действующий параллельно хребту – Дело II – Ветер от нижней части крыши к верхней
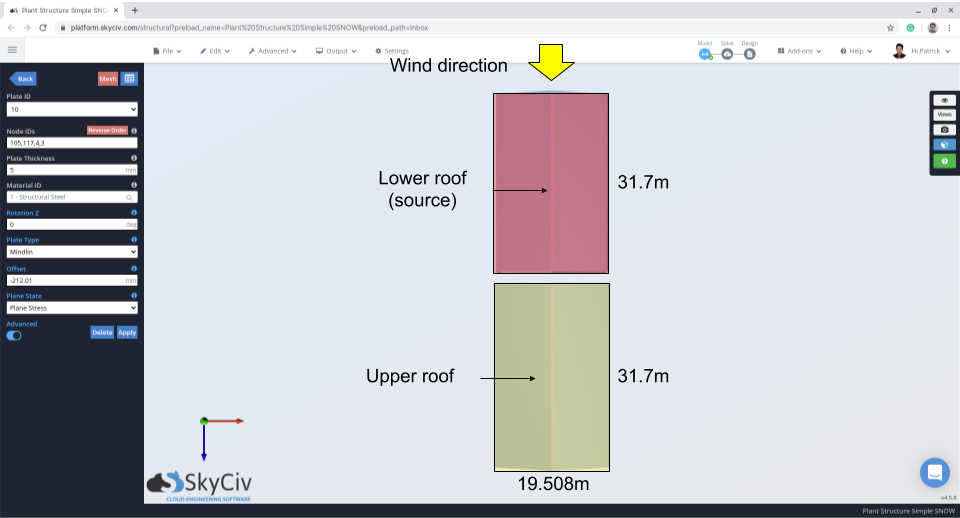
фигура 12: План конструкции с указанием направления ветра и области источника – ветер с нижней крыши на верхнюю.
Для случая II, расчет аналогичен случаю I, но отличается \(β = 0.67\):
\(β = 0.67\)
\({час}^{‘} знак равно (3.5) – \гидроразрыва{(0.8)(1.0)(1.10)}{(2.673)} знак равно 3.17 м )
\({час}_{п} знак равно 0\)
\({{час}_{п}}^{‘} =0\)
\({L}_{cs} знак равно 2(19.507) -{(19.507)}^{2}/(31.7) знак равно 27.01 м )
\(F = 0.35(0.67)\SQRT{\гидроразрыва{(2.673)((27.01) – 5(0))}{(1.10)}} +(0.8) знак равно 2.70\)
\({С}_{а0} = frac{(1.0)(2.673)(3.5)}{(0.8)(1.10)} знак равно 10.631\) или \({С}_{а0} = frac{2.70}{0.8} знак равно 3.375\)
\({С}_{а0} знак равно 3.375\)
\({Икс}_{d} знак равно 5 \гидроразрыва{(0.8)(1.10)}{2.673}(3.375 – 1) знак равно 3.909 м )
в \(х = 0\): \({С}_{а } = 3,375 – (3.375 – 1)(0/3.909) знак равно 3.375\)
в \(x = a\): \({С}_{а } = 3,375 – (3.375 – 1)(2.3/3.909) знак равно 1.978\)
в \(х = {Икс}_{d}\): \({С}_{а } =1.0\)
в \(х = 10{час}^{‘}\): \({С}_{а } =1.0\)
в \(х = 0\): \(S = 0,8((1.10)(0.8)(1.0)(1.0)(3.375) +0.1) знак равно 2.456 kPa\)
в \(x = a\): \(S = 0,8((1.10)(0.8)(1.0)(1.0)(1.978) +0.1) знак равно 1.473 кПа = {п}_{1}\)
в \(х = {Икс}_{d}\): \(S = 0,8((1.10)(0.8)(1.0)(1.0)(1.0) +0.1) знак равно 0.784 кПа = {п}_{2} знак равно {п}_{3}\)
на верхнем уровне крыши: \(S = 0,8((1.10)(0.8)(1.0)(1.0)(1.0) +0.1) знак равно 0.784 kPa\)
Для иллюстрации, соответствующий \({п}_{1}\), \({п}_{2}\), и \({п}_{3}\) показаны на рисунках 13 и 14 ниже для случаев I и II, соответственно.
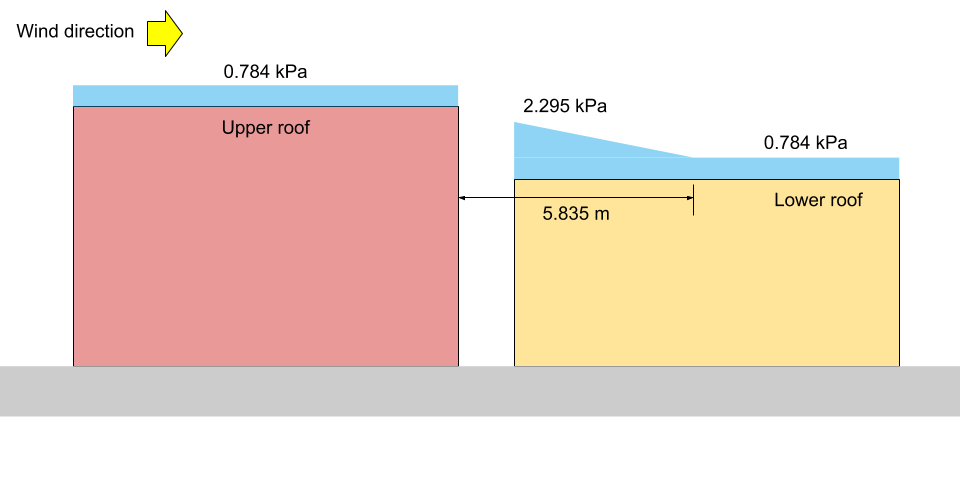
фигура 13: Иллюстрация снеговой нагрузки для случая I (не в масштабе).
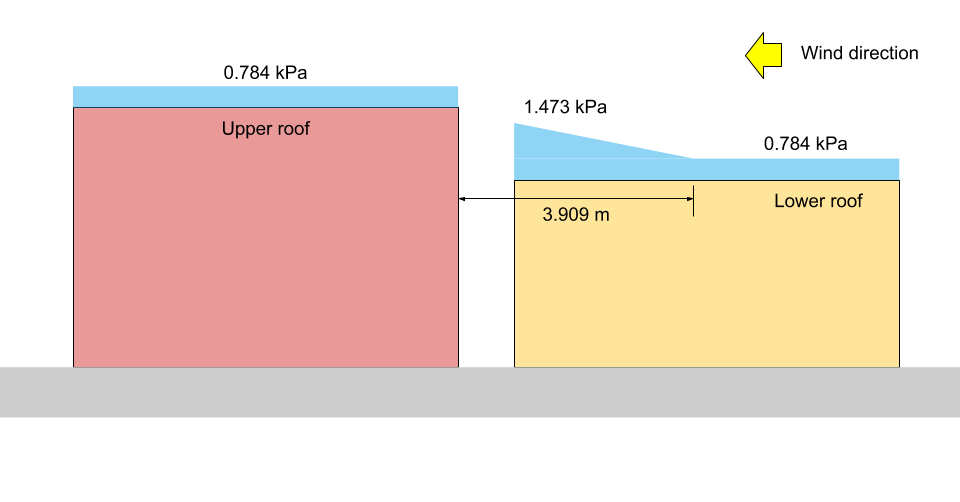
фигура 14: Иллюстрация снеговой нагрузки для варианта II (не в масштабе).
Выполните эти расчеты автоматически за считанные минуты
Это был долгий расчет, что вы можете сделать как инженер, чтобы ускорить этот процесс для ваших будущих проектов? Недавно SkyCiv выпустила и автоматизировала генератор снеговой нагрузки как часть генератора нагрузки SkyCiv., которые также могут создавать ветровые нагрузки. Чтобы найти снеговые нагрузки в показанном примере, это займет всего несколько кликов с помощью инструмента:
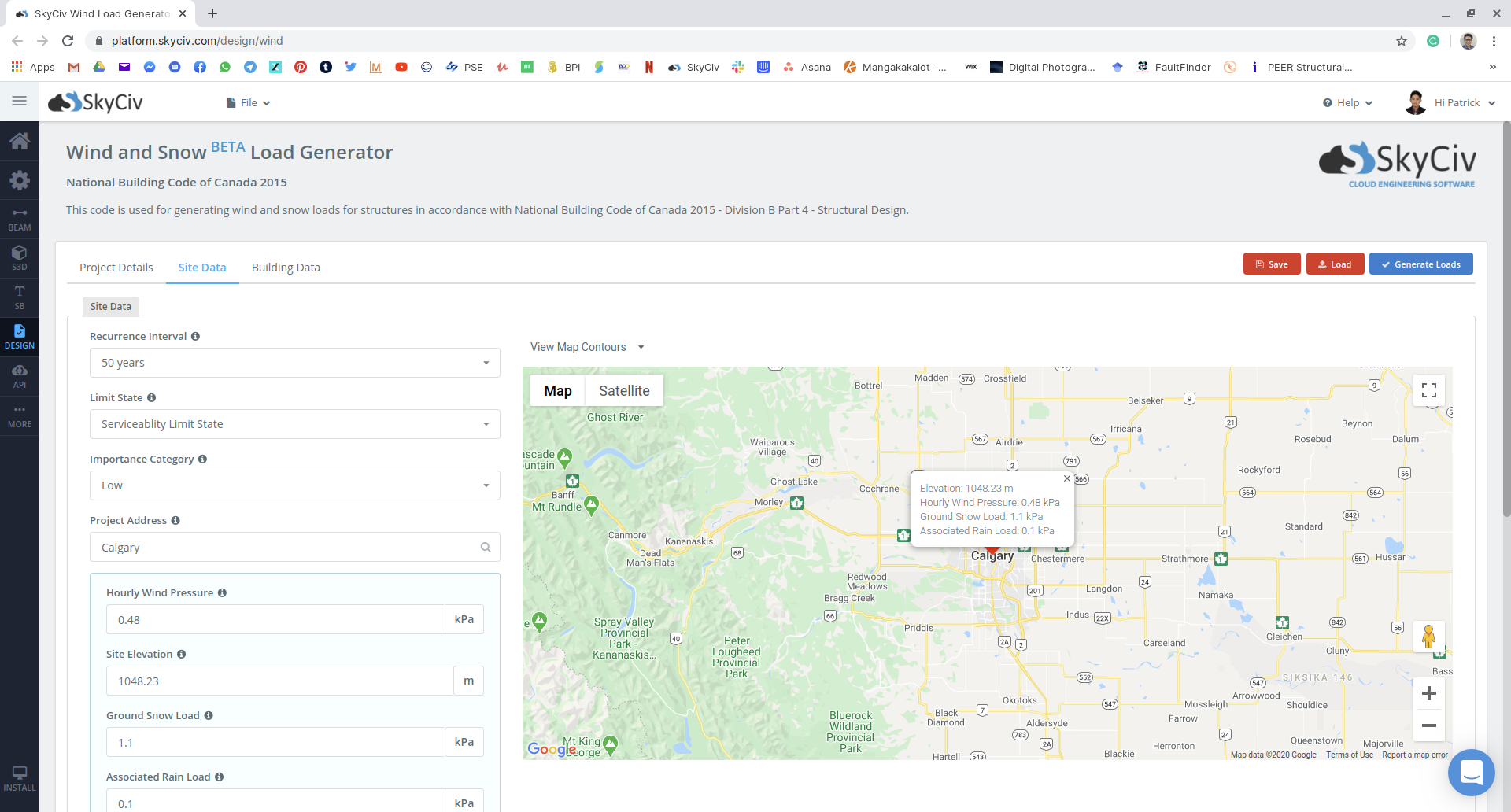
фигура 15: Ввод данных сайта в модуль SkyCiv Load Generator на нашем примере.
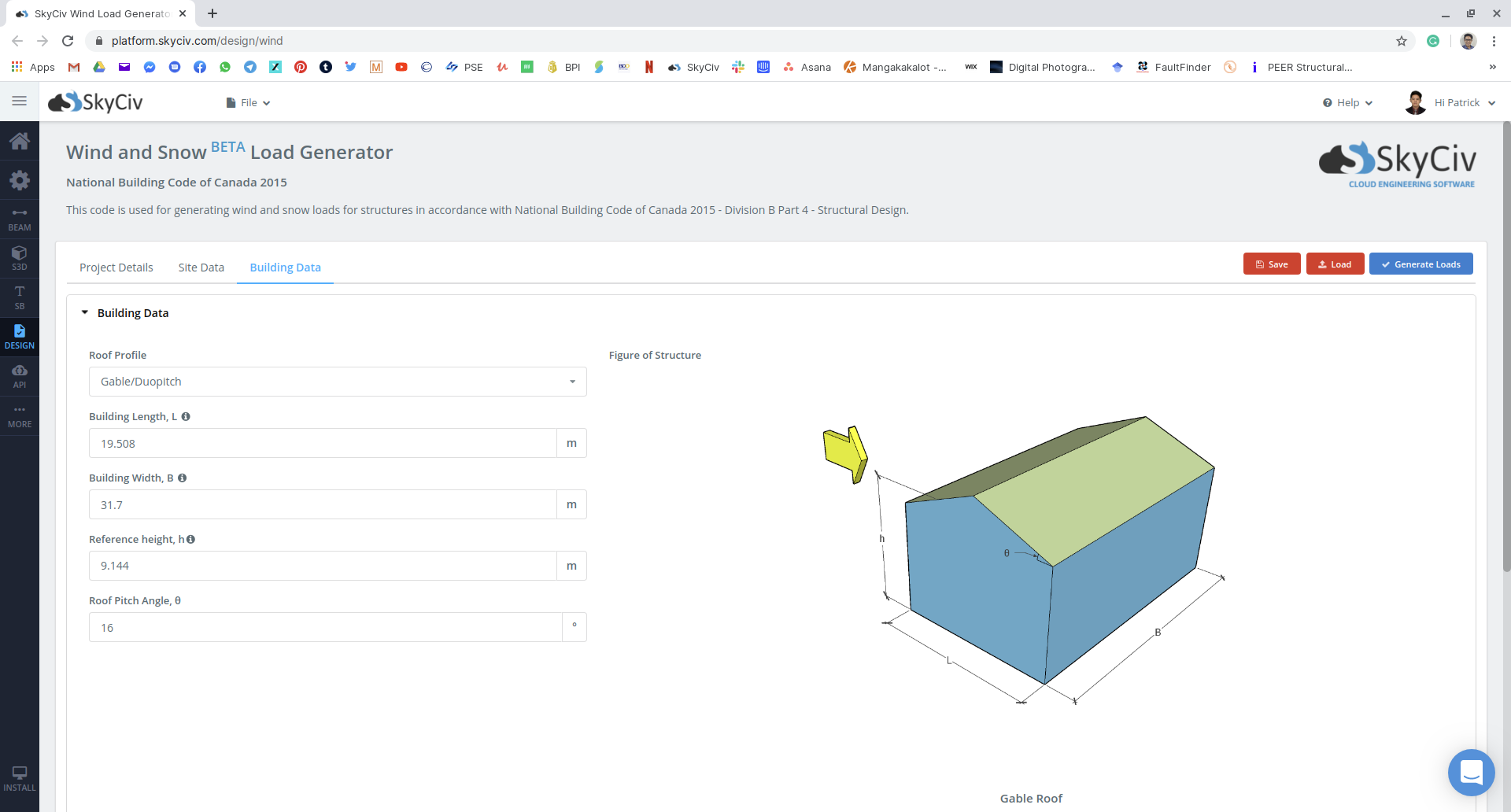
фигура 16: Ввод параметров зданий и снега в модуль SkyCiv Load Generator на нашем примере.
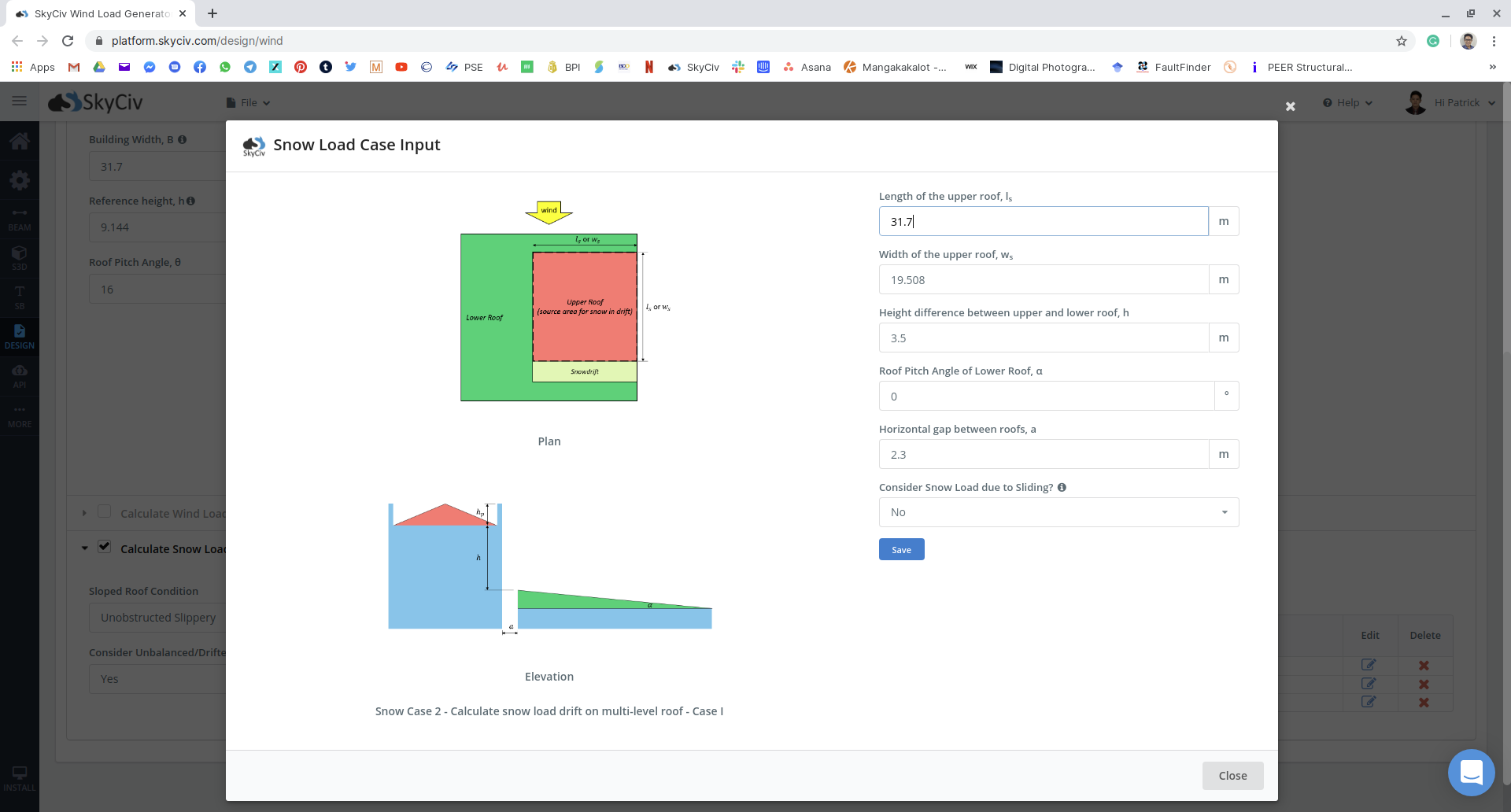
фигура 17: Вход снеговой нагрузки для нескольких несбалансированных случаев для примера.
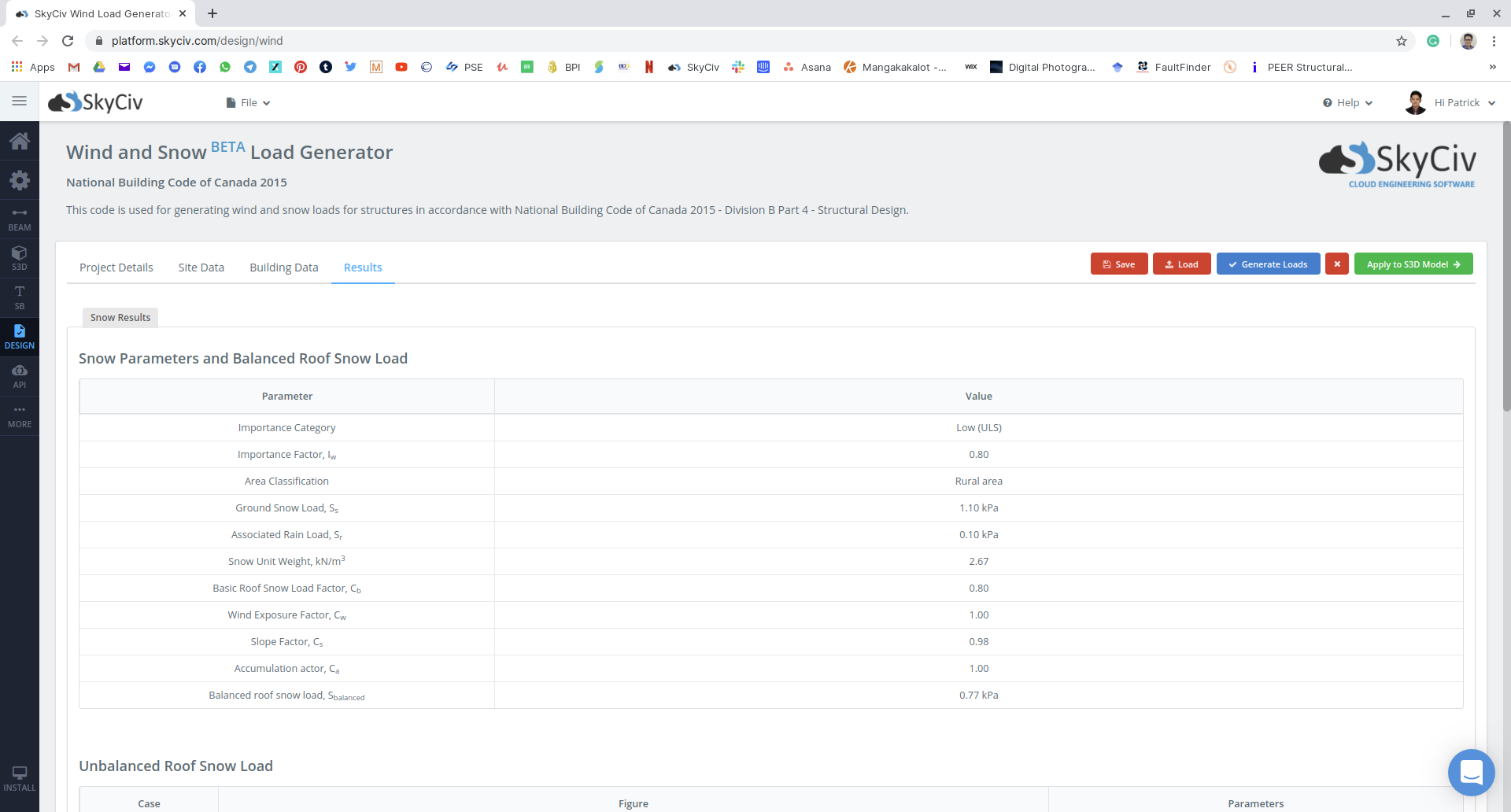
фигура 18: Сводка используемых параметров снеговой нагрузки и сбалансированной снеговой нагрузки, применяемой к конструкции.
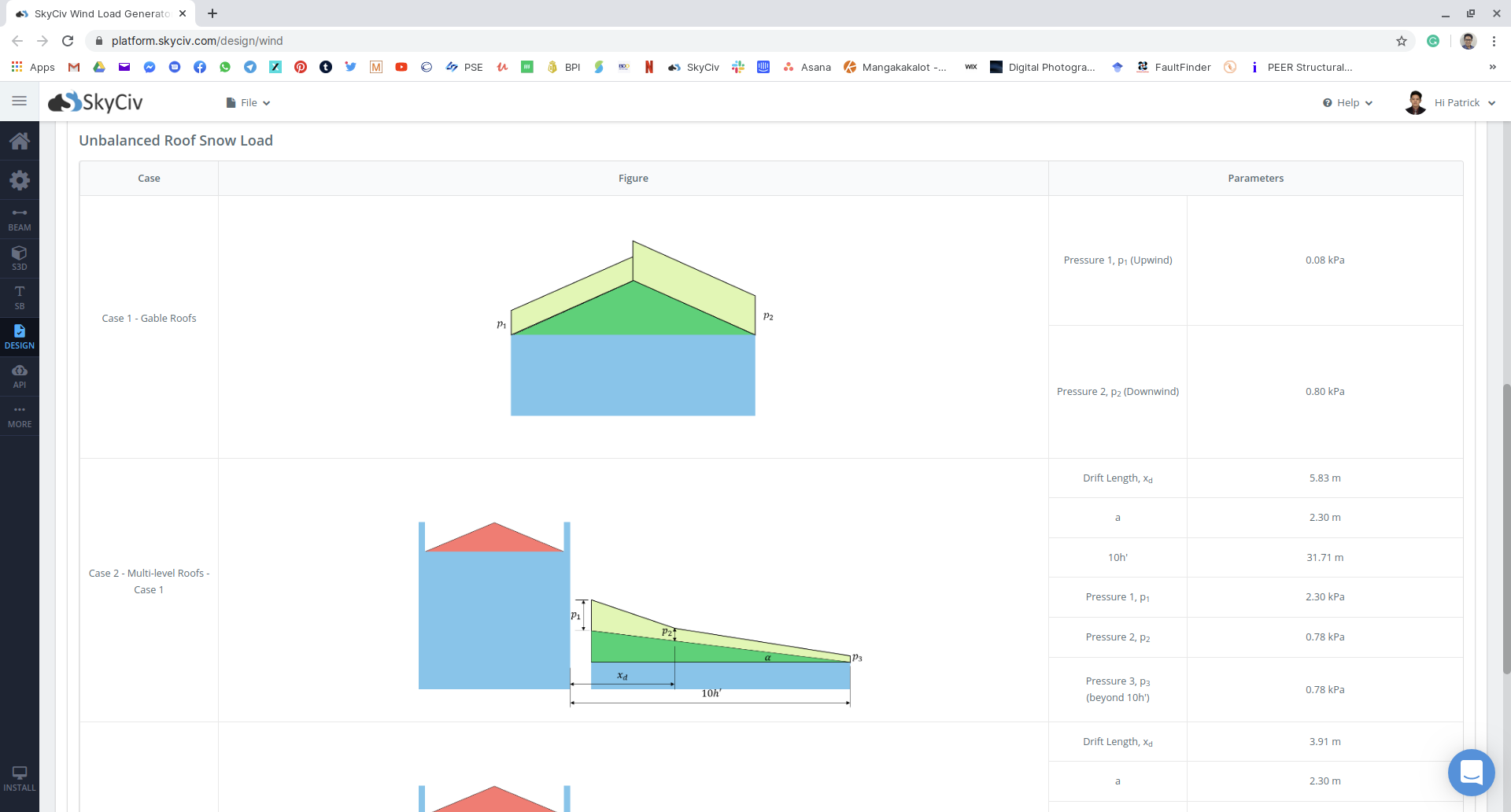
фигура 19: Сводка результатов несбалансированной снеговой нагрузки.
Расчеты снеговой нагрузки в модуле SkyCiv Load Generator поддерживаются ссылочными кодами, такими как ASCE. 7-10, 7-16, В 1991-1-3, NBCC 2015, и AS / NZS 1170.3, и доступен на Standalone (Только генератор нагрузки) и Professional учетные записи. Знаком с программированием и API? Эту функциональность можно автоматизировать с помощью SkyCiv API.
Инженер-строитель, Разработка продукта
MS Гражданское строительство
Ссылки:
- Национальный исследовательский совет Канады. (2015). Национальный строительный кодекс Канады, 2015. Национальный исследовательский совет Канады.
Заметка:
- Ссылка на код NBCC для “Базовый коэффициент снеговой нагрузки на крышу” — Ищу 4.1.6.2 Приговор (2)
- Ссылка на код NBCC для “Фактор воздействия ветра” — Ищу 4.1.6.2 Предложения (3) и (4)
- Ссылка на код NBCC для “Коэффициент наклона” — Ищу 4.1.6.2 Предложения (5), (6), и (7)
- Ссылка на код NBCC для “Фактор накопления” — Ищу 4.1.6.2 Приговор (8), 4.1.6.5 для многоуровневой кровли, 4.1.6.6 для крыш с разрывом, и 4.1.6.9 для двускатных крыш



