Односвайная конструкция в соответствии с AS 2159 (2009) & 3600 (2018)

В случае большой боковой нагрузки или неблагоприятных почвенных условий, свайный фундамент предпочтительнее мелкого фундамента. Чтобы избежать образования свай, можно предпринять такие попытки, как методы модификации почвы., тем не мение, эти методы могут включать дорогостоящие процессы, при этом этот случай, сваи может быть даже дешевле.

Модуль SkyCiv Foundation Design включает в себя проектирование свай в соответствии с Американским институтом бетона. (ACI 318) и австралийские стандарты (ТАК КАК 2159 & 3600).

Хотите попробовать программное обеспечение SkyCiv Foundation Design? Наш бесплатный инструмент позволяет пользователям выполнять расчеты несущей способности без загрузки или установки.!

Калькулятор проектирования фундамента

Расчетная геотехническая прочность сваи

Вертикальные нагрузки, действующие на сваи, воспринимаются концевой опорой сваи и обшивкой или валом - трением по ее длине.. Геотехническая прочность конструкции (р_d,грамм) равна предельной геотехнической прочности (р_{d,а также}) умноженный на геотехнический коэффициент уменьшения (ø_грамм) как указано на ТАК КАК 2159 Раздел 4.3.1.

\({р}_{d,грамм} знак равно {ø}_{грамм} × {р}_{d,а также}\) (1)

р_d,грамм = Расчетная геотехническая прочность

р_{d,а также} = Максимальная геотехническая прочность

ø_грамм = Геотехнический коэффициент уменьшения

Максимальная геотехническая прочность (р_{d,а также})

Предел геотехнической прочности равен сумме факторизованного поверхностного трения сваи. (е_м,s ) умноженное на площадь боковой поверхности и сопротивление основания, умноженное на площадь поперечного сечения на вершине сваи.

\( {р}_{d,а также} знак равно [{р}_{s} × ({е}_{м,s} × {А}_{s} )] + ({е}_{б} × {А}_{б} )\) (2)

р_s = Коэффициент уменьшения сопротивления вала

е_м,s = Сопротивление трению вала

А_s = Площадь боковой поверхности

е_б = Член базового сопротивления

А_б = Площадь поперечного сечения на вершине сваи

Для более подробного руководства, ознакомьтесь с нашей статьей о расчете сопротивление поверхностному трению и несущая способность.

Геотехнический коэффициент уменьшения (ø_грамм)

Геотехнический коэффициент уменьшения - это расчет на основе рисков для окончательного проекта, который учитывает различные факторы., такие как условия сайта, конструкция свай, и установочные факторы. Его значение обычно колеблется от 0.40 в 0.90. ТАК КАК 2159 4.3.1 также указано, как оценить его значение, как показано в уравнении (3).

\( {ø}_{грамм} знак равно {ø}_{ГБ} + [К × ({ø}_{tf} – {ø}_{ГБ})] ≥ {ø}_{ГБ} \) (3)

ø_ГБ = Базовый коэффициент снижения геотехнической прочности

ø_tf = Фактор внутреннего тестирования

K = фактор преимущества тестирования

Факторы выгоды от внутренних испытаний и испытаний зависят от того, какой тип нагрузочного испытания используется на сваях.. Их значения указаны в таблице. 1 и по уравнениям (4) и (5). Нагрузочные испытания свай кратко обсуждаются в разделе 8 AS 2159.

Фактор внутреннего тестирования (øtf)
Статическое нагрузочное тестирование	0.90
Быстрое нагрузочное тестирование	0.75
Испытания на динамическую нагрузку предварительно сформованных свай	0.80
Испытания динамической нагрузкой не готовых свай	0.75
Двунаправленное нагрузочное испытание	0.85
Без тестирования	0.80

Стол 1: Внутренние значения тестового фактора

Фактор преимущества тестирования при статическом нагрузочном тестировании:

\( K = frac{1.33 × p}{п + 3.3} ≤ 1\) (4)

Фактор преимущества тестирования для тестирования динамической нагрузки:

\( K = frac{1.13 × p}{п + 3.3} ≤ 1\) (5)

p = Процент от общего числа свай, которые проверены и соответствуют критериям приемки.

Базовый коэффициент снижения геотехнической прочности оценивается с использованием процедуры оценки риска, описанной в разделе 4.3. AS 2159. Результатом указанной процедуры является индивидуальный рейтинг риска. (IRR) и общий дизайн Средний рейтинг риска (ARR) который должен использоваться для определения значения ø_ГБ как показано в таблице 2.

Базовый коэффициент снижения геотехнической прочности (øГБ)
Средний рейтинг риска (ARR)	Категория риска	øГБ для систем с низким уровнем резервирования	øГБ для систем с высоким резервированием
ARR ≤ 1.5	Очень низкий	0.67	0.76
1.5 < ARR ≤ 2.0	От очень низкой до низкой	0.61	0.70
2.0 < ARR ≤ 2.5	Низкий	0.56	0.64
2.5 < ARR ≤ 3.0	От низкого до среднего	0.52	0.60
3.0 < ARR ≤ 3.5	умеренный	0.48	0.56
3.5 < ARR ≤ 4.0	От умеренного до высокого	0.45	0.53
4.0 < ARR ≤ 4.5	Высокая	0.42	0.50
ARR > 4.5	Очень высоко	0.40	0.47

Стол 2: Значения базового геотехнического коэффициента восстановления, (ТАК КАК 2159 Стол 4.3.2)

Системы с низким уровнем резервирования представляют собой сильно нагруженные одиночные сваи, в то время как системы с высоким уровнем резервирования включают большие группы свай под большими крышками свай или группы свай с более чем 4 геморрой.

Конструктивная прочность конструкции

Сваи конструктивно устроены практически так же, как колонны.. Расчетная прочность конструкции (р_d,s) требует предельных возможностей, такие как осевые и поперечные силы, и изгибающий момент. Расчетная конструкционная прочность бетонной сваи эквивалентна пределу расчетной прочности. (р_нас) уменьшается на коэффициент снижения прочности (ø_s) и коэффициент размещения бетона (К), как указано в разделе 5.2.1 AS 2159.

\( {р}_{d,s} знак равно {ø}_{s} × к × {р}_{нас} \) (6)

ø_s = Коэффициент снижения прочности

k = коэффициент размещения бетона

р_нас = Максимальная прочность конструкции

Значения коэффициента снижения прочности приведены в таблице. 3. Фактор размещения бетона колеблется от 0.75 в 1.0, в зависимости от способа строительства сваи. тем не мение, для свай кроме бетона и раствора, k следует принять как 1.0.

Факторы снижения силы (ø)
Осевое усилие без изгиба	0.65
Гибка без осевого усилия (øpb)	0.65 ≤ 1.24 – [(13 × kуо)/12] ≤ 0.85
Гибка с осевым сжатием:
(я) NU ≥ Nуб	0.60
(II) NU < Nуб	0.60 + {(øpb – 0.66) × [1 – (NU/Nуб)]}
ножницы	0.70

Стол 3: Факторы снижения силы (Стол 2.2.2, ТАК КАК 3600-18)

Осевая и изгибная способности одиночной сваи

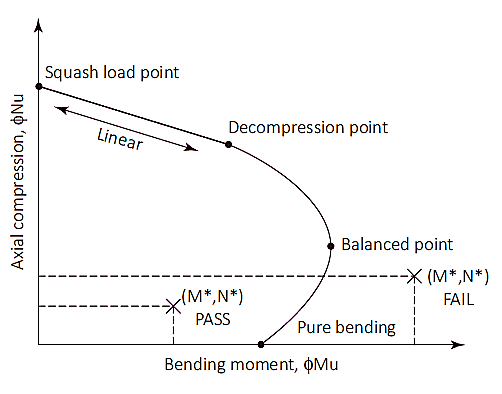
Подобно столбцам, сваи также могут подвергаться комбинированной сжимающей и изгибающей нагрузке.. Осевая и изгибная способности проверяются с помощью диаграммы взаимодействия. Эта диаграмма представляет собой визуальное представление поведения изгибных и осевых нагрузок, вызванных увеличением нагрузки от чистой точки изгиба до достижения точки равновесия..

 

фигура 1: Схема взаимодействия столбцов

Сквош нагрузки (N_уо)

Точка нагружения при сжатии - это точка на диаграмме, где свая разрушится при чистом сжатии.. С этой точки зрения, осевая нагрузка приложена к пластическому центру тяжести сечения, чтобы оставаться в сжатом состоянии без изгиба. Сквош нагрузка (N_уо) и расположение пластикового центроида (d_Q) вычисляются, как показано в уравнениях (7) & (8). Хотя расположение пластикового центроида можно принять как 1/2 общей глубины поперечного сечения для симметричных сечений с симметричным расположением арматуры.

\( {ϕN}_{уо} = ø × [({А}_{грамм} – {А}_{s}) × ({а }_{1} × f’c) + ({А}_{s} × {е}_{его})] \) (7)

А_грамм = Общая площадь поперечного сечения

А_s = Общая площадь стали

а ₁ знак равно 1.0 – (0.003 × f’c) [0.72 ≤α₁ ≤0,85]

f’c = Прочность бетона

е_его = Предел текучести стали

\( {d}_{Q} = Гидроразрыва{[(b × D) – {А}_{s}] × ({а }_{1} × f’c) × сумма_{я = 1}^{N} ({А}_{с} × {е}_{его} × {d}_{йи})}{{N}_{уо}} \) (8)

b = ширина сваи в поперечном сечении

D = Глубина или диаметр поперечного сечения сваи

А_с = Рассматриваемая площадь арматурного стержня

d_йи = Рассматриваемая глубина арматурного стержня

От точки сжатия до точки декомпрессии

Точка декомпрессии - это место, где деформация бетона в крайнем сжимающем волокне равна 0.003 а деформация в крайнем растяжимом волокне равна нулю. Прочность сваи между сжимающей нагрузкой и точками декомпрессии может быть рассчитана путем линейной интерполяции с коэффициентом уменьшения прочности. (ø_s) из 0.6.

От точки декомпрессии до чистого изгиба

Чистая точка изгиба - это точка, при которой осевая нагрузка равна нулю.. При переходе от точки декомпрессии к чистому изгибу используется коэффициент снижения прочности, равный 0.6 в 0.8 и входной параметр (К_U) вводится. Значение k_U начинается в 1 в точке декомпрессии и уменьшается до достижения чистого изгиба. Между переходом двух точек, достигается сбалансированное состояние. С этой точки зрения, бетонная деформация на пределе (е_с= 0,003) и внешняя деформация стали достигает текучести (е_s= 0,0025), Значение k_U на данный момент примерно 0.54 с коэффициентом снижения прочности 0.6.

Как только значение k_U выбран, растягивающие и сжимающие силы секции могут быть рассчитаны. Осевая нагрузка на сечение эквивалентна сумме растягивающих и сжимающих сил., в то время как изгибающий момент рассчитывается путем разрешения этих сил относительно нейтральной оси. Расчет для сжимающих и растягивающих сил перечислен ниже.

Сила из-за бетона (F_cc):

\( {F}_{cc} знак равно {а }_{2} × f’c × {А}_{с} \) (9)

а ₂ знак равно 0.85 – (0.0015 × f’c) [а _{2 ≥}0.67]

А_с = Площадь блока сжатия (см. рисунок 2)

= b × γ × к_U × d (прямоугольное сечение)

знак равно(1/2) × (θ – sinθ) × (D / 2)² (круглое сечение)

γ = 0.97 – (0.0025 × f’c) [с _≥0.67]

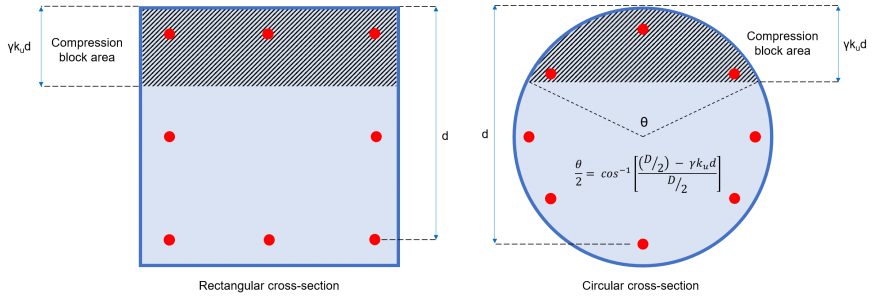
фигура 2: Бетонный блок сжатия

Сила (F_и) и момент (M_я) вклад каждого отдельного бара:

Каждый арматурный стержень секции оказывает силу, которая может быть сжимающей или растягивающей., в зависимости от величины деформации стержня (е_и) показано в уравнении (10).

\( {е}_{и} = frac{{е}_{с}}{({К}_{U} × d)} × [({К}_{U} × d) – {d}_{йи}] \) (10)

d_йи = Глубина до рассматриваемого стержня

е_с= Деформация бетона = 0.003

Если ε_и < 0 (штанга в напряжении)

Если ε_и > 0 (бар находится в сжатии)

Бар в сжатии:

\( {F}_{и} знак равно {σ}_{и} × {А}_{с} \) (11)

σ_и = Напряжение в барах = Минимум [(е_и × Е_s ), е_его]

Е_s = Модуль упругости стали

А_с = Барная зона

Штанга в напряжении:

\( {F}_{и} знак равно [{σ}_{и} – ({а }_{2} × f’c)] × {А}_{с} ≥ 0\) (12)

σ_и = Напряжение в барах = Минимум [(е_и × Е_s ), –е_его]

Е_s = Модуль упругости стали

А_с = Барная зона

Момент у каждого бара:

\( {M}_{я} знак равно {F}_{и} × {d}_{йи} \) (13)

Осевая вместимость сваи:

\( {остров}_{U} = ø × [ {F}_{cc} + {Σ}_{я = 1}^{N} {F}_{и}]\) (14)

Изгибная способность сваи:

\( {воспаленный}_{U} = ø × [ ({N}_{U} × {d}_{Q}) – ({F}_{cc} × {и}_{с}) – {Σ}_{я = 1}^{N} {M}_{я}] \) (15)

Расчетный изгибающий момент:

Раздел 7.2 указывает, что сваи должны иметь допуск на смещение 75 мм для горизонтального позиционирования свай.. Это требование может вызвать изгибающий момент, равный осевой нагрузке, умноженной на эксцентриситет 75 мм.. Дополнительно, также следует учитывать минимальный расчетный момент, который эквивалентен осевой силе, умноженной на 5% от общей минимальной ширины ворса. Следовательно, расчетный изгибающий момент должен быть большим значением между уравнениями 16a и 16b..

\( {M}_{d} знак равно {{M}^{*}}_{применяемый} + ({N}^{*} × 0.075 м) \) (16а )

\( {M}_{d} знак равно {N}^{*} × (0.05 × D) \) (16б)

M_d = Расчетный изгибающий момент

М *_{применяемый} = Примененный момент

N * = осевая нагрузка

D = ширина сваи

Прочность на сдвиг одиночной сваи

Расчет прочности на сдвиг должен производиться в соответствии с Разделом 8.2 AS 3600. Прочность на сдвиг эквивалентна совокупной прочности на сдвиг бетона и стальной арматуры. (уравнение 17).

\( {практика}_{U} = ø × ({V}_{uc} + {V}_{нас}) ≤ {практика}_{U,Максимум} \) (17)

Прочность бетона на сдвиг (V_uc)

Вклад бетона в способность к сдвигу рассчитывается, как показано в уравнении (18) который определен в разделе 8.2.4.1 AS 3600. Этот раздел также требует, чтобы значение √f’c не превышало 9.0 МПа. Значения параметра k_v и θ_v определяются с помощью упрощенного метода, предложенного в Разделе 8.2.4.3 AS 3600.

\( {V}_{uc} знак равно {К}_{v} × б × {d}_{v} × sqrt{f'c} \) (18)

d_v = Эффективная глубина сдвига = Максимум [(0.72 × D ), (0.90 × d )]

Определение минимальной площади поперечной арматуры (А_св.мин) & К_v:

Площадь сдвига арматуры (А_св) это общая площадь всех предоставленных стальных стержней, привязанных в одном направлении от приложенной нагрузки.. Раздел 8.2.1.7 AS 3600 предоставил уравнение для минимальной поперечной поперечной поперечной прочности арматуры, который будет:

\( \гидроразрыва{{А}_{св.мин}}{s} = frac{0.08 × sqrt{f'c} × б}{{е}_{sy.f}} \)

е_sy.f = Предел текучести арматурных стержней на сдвиг

s = Расстояние между центрами поперечных арматурных стержней

Для (А_св/s) < (А_св.мин/s):

\( {К}_{v} = frac{200}{[1000 + (1.3 × {d}_{v} )]} ≤ 0.10\)

Для (А_св/s) ≥ (А_св.мин/s):

\( {К}_{v} знак равно 0.15 \)

Прочность на сдвиг стальных стержней (V_нас)

Вклад поперечной сдвиговой арматуры в вычисленную сдвигающую способность показан в уравнении (19), который определен в разделе 8.2.5 AS 3600.

\( {V}_{нас} = frac{{А}_{св} × {е}_{sy.f} × {d}_{v}}{s} × детская кроватка{θ}_{v} \) (19)

θ_v= угол наклона стойки сжатия = 36º

Максимальная прочность на сдвиг (V_u.max)

Прочность на сдвиг ограничена и ни в коем случае не должна превышать максимальное значение, указанное в разделе 8.2.6 AS 3600 (уравнение 20).

\( {V}_{u.max} знак равно 0.55 × [ (f’c × b × {d}_{v}) × гидроразрыв{детская кроватка{θ}_{v} + детская кроватка{а }_{v}}{1 + детская кроватка ^{2}{θ}_{v} }] \) (20)

а _v= угол между арматурой, работающей на наклонный сдвиг, и продольной растянутой арматурой ≈ 90º

Максимальная прочность на сдвиг (V_U)

Общая прочность на сдвиг, вносимая бетоном и арматурой на сдвиг, должна быть меньше или равна предельному значению V._u.max

\( {V}_{U} знак равно ({V}_{uc} + {V}_{нас} ) ≤ {V}_{u.max} \) (21)

Расчетная прочность на сдвиг (практика_U)

Коэффициент уменьшения емкости, который должен применяться для определения предела прочности на сдвиг, составляет ø = 0.7. Следовательно, Расчетная прочность сваи на сдвиг определяется выражением:

\( {практика}_{U} = ø × ({V}_{uc} + {V}_{нас} ) \) (22)

Ссылки

• Пакет, Лонни (2018). Австралийское руководство для инженеров-строителей. CRC Press.
• Проектирование и установка свай (2009). ТАК КАК 2159. Австралийский стандарт
• Бетонные конструкции (2018). ТАК КАК 3600. Австралийский стандарт