Односвайная конструкция в соответствии с ACI 318 (2014)

Сваи - это длинные и тонкие элементы, которые переносят нагрузки от надстройки на более глубокую почву или на скалу с соответствующей несущей способностью.. Материалы, используемые для свай, могут включать дерево., стали, и бетон. Установка сваи в грунт возможна забивная., пробурили, или домкратом, которые затем соединяются с заглушками. Много факторов, такие как условия сайта, тип почвы, передача грузов, считаются классифицирующими по типу и установке свай. В этой статье основное внимание уделяется проектированию бетонной сваи в соответствии с Американским институтом бетона. (ACI) 318 – 2014.

Модуль SkyCiv Foundation Design включает в себя проектирование свай, соответствующее требованиям Американского института бетона. (ACI 318) и австралийские стандарты (ТАК КАК 2159 & 3600).

Хотите попробовать программное обеспечение SkyCiv Foundation Design? Наш бесплатный инструмент позволяет пользователям выполнять расчеты несущей способности без загрузки или установки.!

Калькулятор проектирования фундамента

Несущая способность сваи

В общем-то, вертикальные нагрузки, действующие на сваи, воспринимаются концевой опорой сваи, и сопротивление трению кожи развивалось по всей длине. Максимальная грузоподъемность (Q_U) должен быть представлен уравнением (1). Коэффициент запаса прочности применяется для расчета допустимой грузоподъемности. (Q_А).

\({Q}_{U} знак равно {Q}_{п} + {Q}_{s}\) (1)

Q_U = Максимальная грузоподъемность

Q_п = Сопротивление концевого подшипника

Q_S = Сопротивление поверхностному трению

\({Q}_{А} = frac{{Q}_{U}}{FOS} \) (2)

Q_А = Допустимая грузоподъемность

FOS = коэффициент безопасности

Для более подробного руководства, ознакомьтесь с нашей статьей о расчете сопротивление поверхностному трению и несущая способность.

Конструктивная прочность одиночной сваи

На сваи также действуют осевые силы., сдвигающая сила, и изгибающий момент, поэтому они конструктивно похожи на колонны. Раздел 10.5.1.1 заявляет, что вся факторная нагрузка не должна превышать соответствующую расчетную прочность.

\( {Op}_{N} ≤ {п}_{U} \) (3а )

\( {воспаленный}_{N} ≤ {M}_{U} \) (3б)

\( {практика}_{N} ≤ {V}_{U} \) (3с)

п_U, M_U, V_U = Фактор осевой, изгибающий момент, поперечные нагрузки

п_N, M_N, V_N = Номинальный осевой, изгибающий момент, поперечные нагрузки

ø = Коэффициенты снижения прочности (Стол 1)

Факторы снижения силы(φ)
аксиальный	0.65-0.90
гибкий	0.65-0.90
ножницы	0.75

Стол 1: Факторы снижения силы (Стол 21.2.1, ACI 318-14)

Прочность на сдвиг одиночной сваи (практика_N)

Номинальная прочность на сдвиг должна быть эквивалентна совокупному вкладу прочности на сдвиг бетона и стальной арматуры..

Прочность бетона на сдвиг (V_с)

Вклад бетона в способность к сдвигу рассчитывается, как показано в уравнении (4) который определен в разделе 22.5.5.1 ACI 318-14.

\( {V}_{с} знак равно 0.17 × λ × sqrt{Ь»} × б × г \) (4)

λ = коэффициент модификации бетона = 1 (Бетон нормального веса, Стол 19.2.4.2)

Ь’ = Прочность бетона

b = ширина или диаметр сваи

d = 0.80 × глубина сваи (Раздел 22.5.2.2)

Прочность на сдвиг стальных стержней (V_s)

Вклад поперечной поперечной арматуры в сдвигающую способность вычисляется как минимум между уравнениями (5) и (6).

\( {V}_{s} знак равно 0.066 × sqrt{Ь»} × б × г \) (5)

\( {V}_{s} = frac{{А}_{v} × {е}_{уг} × d }{s} \) (6)

А_V = Площадь поперечных арматурных стержней

е_уг = Предел текучести арматурных стержней на сдвиг

s = Расстояние между центрами поперечных арматурных стержней

Номинальная прочность на сдвиг (практика_N)

Подводя итоги вывода уравнения 4-6 должно привести к номинальной прочности сваи на сдвиг. Фактор снижения прочности (ø) должен быть равен 0.75 как определено в таблице 22.2.1 ACI 318-14.

\( {практика}_{N} = ø × ({V}_{с} + {V}_{s}) ≤ {практика}_{U} \) (7)

Калькулятор проектирования фундамента

Осевая и изгибная способности одиночной сваи (Op_N, воспаленный_N )

Осевая и изгибная способности проверяются с помощью диаграммы взаимодействия. Эта диаграмма представляет собой визуальное представление поведения изгибных и осевых нагрузок, вызванных увеличением нагрузки от чистой точки изгиба до достижения точки равновесия..

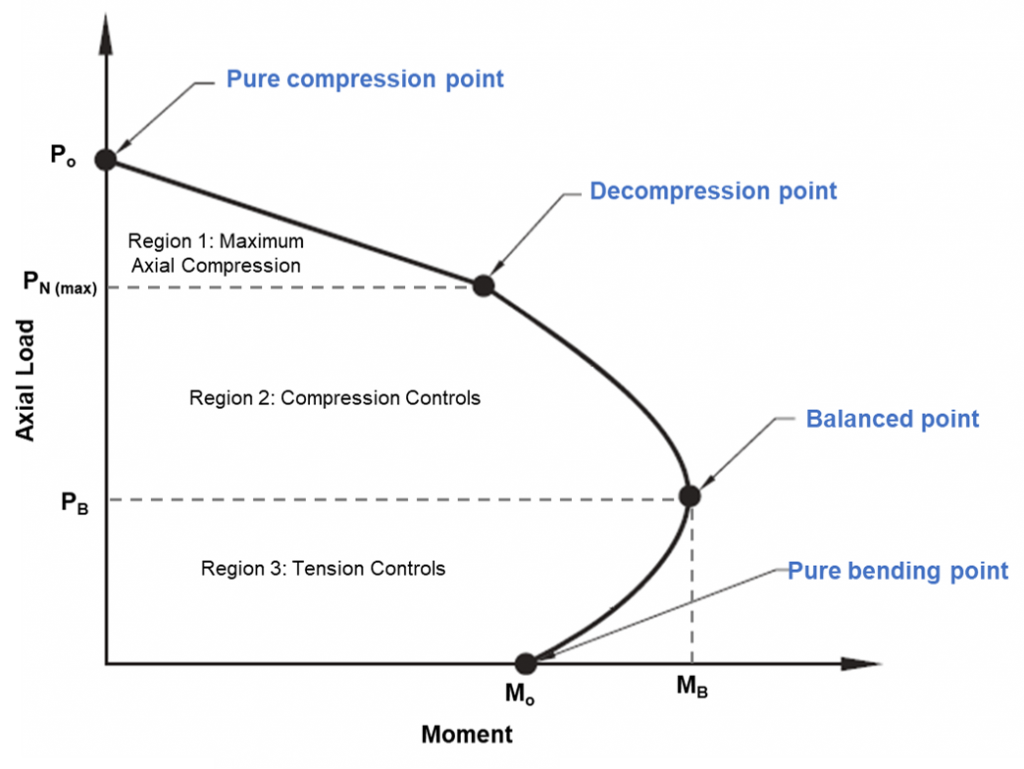
фигура 1: Диаграмма взаимодействия столбцов

Схема взаимодействия столбцов

Точка чистого сжатия на диаграмме - это то место, где сваю не сжимается полностью.. С этой точки зрения, осевая нагрузка приложена к пластическому центру тяжести сечения, чтобы оставаться в сжатом состоянии без изгиба. Прочность сваи между точками чистого сжатия до точек декомпрессии можно рассчитать с помощью линейной интерполяции. Точка декомпрессии - это когда деформация бетона в крайнем сжимающем волокне равна 0.003, а деформация в крайнем растяжимом волокне равна нулю. Чистая точка изгиба - это точка, при которой осевая нагрузка равна нулю.. Между переходом от точки декомпрессии к точке чистого изгиба, достигается сбалансированное состояние. С этой точки зрения, бетонная деформация на пределе (е_с= 0,003), и внешняя деформация стали достигает текучести (е_s= 0,0025). Любая комбинация осевой нагрузки и изгибающего момента за пределами диаграммы приведет к отказу.

Максимальная номинальная осевая прочность на сжатие для расчета (Op_N)

Расчетная осевая прочность секции должна быть ограничена только 80-85% номинальной осевой прочности для учета случайного эксцентриситета.

\( {Op}_{N} = ø × {п}_{О} \) (8а )

\( {п}_{О} = F × [0.85 × {е}_{с} × ({А}_{грамм} – {А}_{улица}) + ({е}_{и} × {А}_{улица}) ] \) (8б)

F = 0.80 (связи)

F = 0.85 (спиральный)

А_грамм = Общая площадь поперечного сечения сваи

А_улица = Общая площадь продольных стальных стержней

е_и = Предел текучести стальных стержней

Номинальная прочность на изгиб (воспаленный_N)

Построение диаграммы взаимодействия для столбца включает построение ряда значений P_N И м_N. Значения для P_N должен быть эквивалентен сумме сил растяжения и сжатия., как показано на рисунках 2a и 2b, а соответствующее M_N вычисляется путем разрешения этих сил относительно нейтральной оси. Эти силы включают в себя сжимающую силу, действующую на зону сжатия, и силы, оказываемые каждым из арматурных стержней, которые могут быть сжимающими или растягивающими.. Ниже предлагается общая процедура построения диаграммы взаимодействия с использованием представленных уравнений.

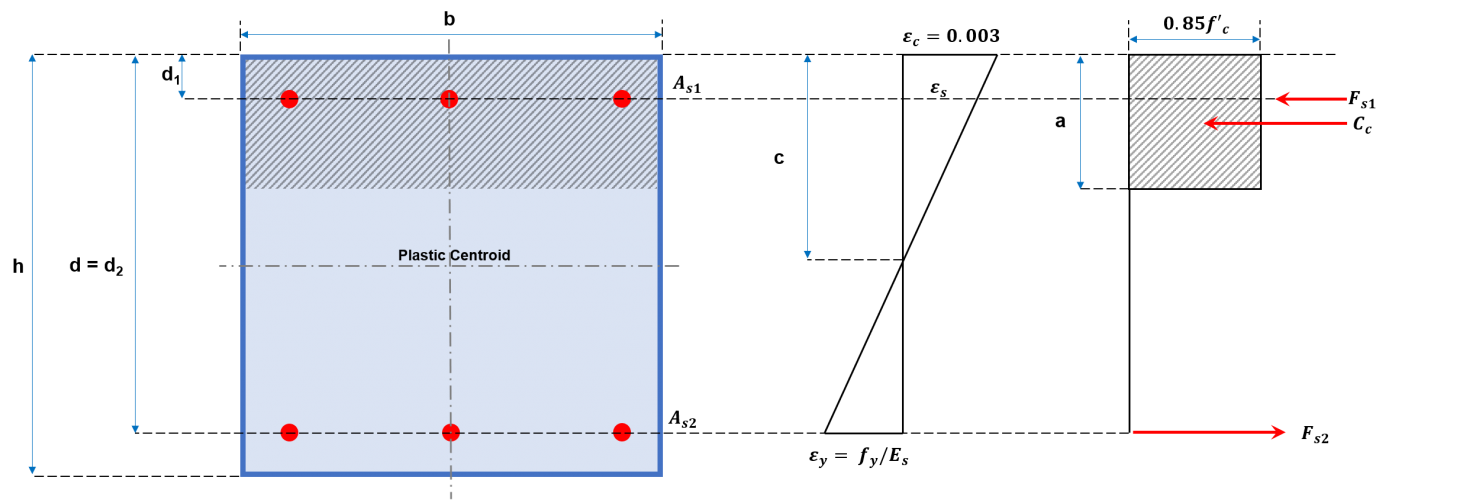
Рисунок 2а: Прямоугольная колонна в поперечном сечении

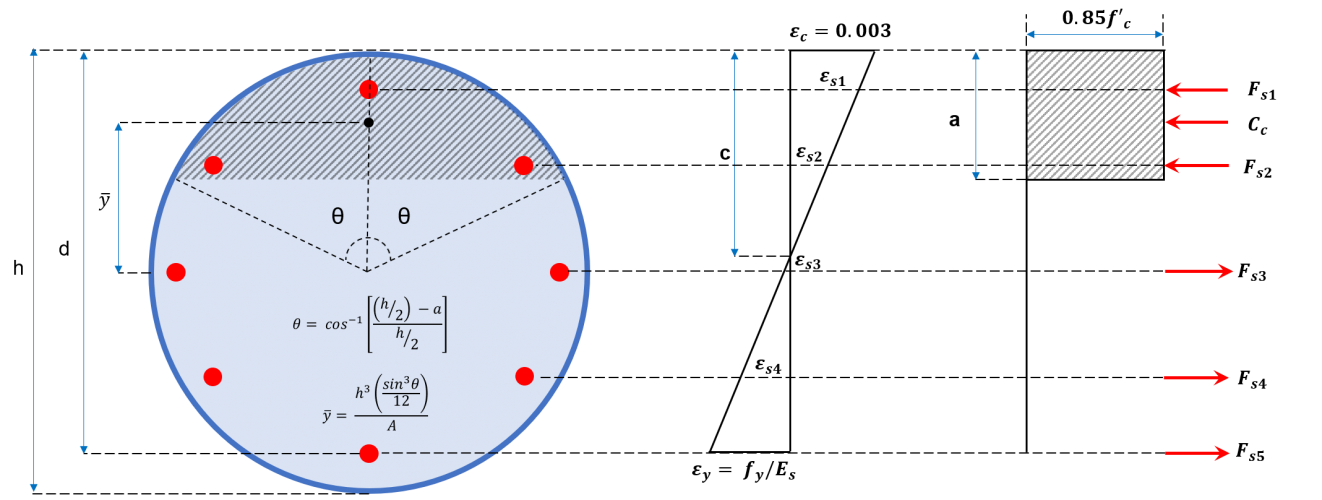
Рисунок 2b: Круглое поперечное сечение колонны

Общий порядок построения диаграммы взаимодействия колонны

(1) Вычислить значение P_О и P_N (уравнения 8a и 8b).

(2) Определите c и деформации в арматуре.

\( c = 0.003 × гидроразрыв{{d}_{1}}{0.003 + (С УЧАСТИЕМ + {е}_{и})} \) (9)

c = глубина нейтральной оси

е_и = Деформация стали = f_и/Е_s

Z = произвольное значение (0, -0.5, -1.0, -2.5)

Следует рассмотреть ряд случаев, выбрав различные положения нейтральной оси., с. Чтобы установить положение нейтральной оси, различные деформации стали выбираются путем умножения произвольного значения Z на предел текучести стали.. Существует широкий диапазон значений Z. тем не мение, есть только четыре обязательных точки для использования на диаграмме взаимодействия.

• Z = 0: с этой точки зрения, деформация в крайнем слое при растяжении равна нулю. Эта точка отмечает переход от стыковки внахлест со сжатием, разрешенной на всех продольных стержнях, к стыковке внахлест с натяжением..
• Z = -0.5: это распределение деформации влияет на длину стыка внахлест в колонне. & обычно наносится на диаграмму взаимодействия.
• Z = -1: это отмечает точку сбалансированного состояния. Это распределение деформации отмечает переход от отказов сжатия, возникающих из-за раздавливания поверхности сжатия секции, до отказов при растяжении, вызванных текучестью продольной арматуры..
• Z = -2.5: эта точка соответствует пределу контролируемой деформации 0.005.

(3) Расчет напряжений в слоях армирования.

\({е}_{и} знак равно{е}_{и} × {Е}_{s} \) (10)

е_и = Напряжение в стали

е_и = Деформация в стали

\({е}_{и} = frac{с -{d}_{я}}{с} × 0.003 \) (11)

Е_s = Модуль упругости стали

(4) Определите высоту блока напряжения сжатия, а .

\(а = {б}_{1} × c \) (а ≤ ч)(12)

Для f’c ≤ 4000 фунтов на квадратный дюйм (28 МПа):

б₁ знак равно 0.85

Для f’c > 4000 фунтов на квадратный дюйм (28 МПа):

\( {б}_{1} знак равно 0.85 – \гидроразрыва{0.05 × (f'c – 4000)}{1000} \) (имперский)

\( {б}_{1} знак равно 0.85 – \гидроразрыва{0.05 ×(f'c – 28)}{7} \) (метрический)

(5) Расчет сил в бетоне и стали.

Площадь блока напряжений сжатия:

\({А}_{с} = а × б \) (Прямоугольное сечение)

\({А}_{с} знак равно{час}^{2} × гидроразрыв{θ – sinθ cosθ}{4} \) (Круглое сечение)

Сила сжатия в бетоне:

\({С}_{с} знак равно (0.85 × f’c) × {А}_{с}\) (14)

Сила растяжения в стали (d_я≤ а):

\({F}_{и} знак равно {е}_{и} × {А}_{и} \) (15)

Сила сжатия в стали (d_я > а ):

\({F}_{и} знак равно [{е}_{и} – (0.85 × f’c)] × {А}_{и} \) (16)

(6) Рассчитайте осевую нагрузку (п_N).

\({п}_{N} знак равно {С}_{с} + Σ {F}_{и} \) (17)

(7) Рассчитайте изгибную способность (M_N).

\({M}_{N} знак равно [{С}_{с} × (\гидроразрыва{час}{2} – \гидроразрыва{а }{2})]+ Σ [{F}_{и} × (\гидроразрыва{час}{2} – {d}_{я}) \) (18)

(8) Вычислить значение коэффициента снижения прочности (ø).

Как показано в таблице 1, коэффициент снижения прочности как для осевого, так и для изгиба варьируется от 0.60 в 0.90. Раздел 21.2 ACI 318-14 демонстрирует свою ценность на данный момент, осевая сила, или комбинированный момент и осевая сила, как показано в таблице 2 ниже.

классификация	спиральный	связанный
Сжатие контролируемое	0.75	0.65
Переход от сжатия к растяжению	0.75 + [50 × (еT – 0.003) ]	0.65 + [(250/3) × (еT – 0.003) ]
Контроль натяжения	0.90	0.90

Стол 2: Коэффициенты снижения прочности для осевого, момент или сочетание осевого и моментного (Стол 21.2.2, ACI 318-14)

(9) Повторите шаги 2-8 с различными значениями Z.

(10) Нанесите на диаграмму значения øP_N и øM_N.

Расчет бетонных свай с помощью бесплатного калькулятора фундамента SkyCiv

Бесплатный калькулятор фундамента SkyCiv поможет вам с проектированием бетонных свай и другими задачами, такими как проектирование фундаментов и бетонных свай. Проверьте это прямо сейчас, чтобы узнать, как наш калькулятор может помочь вам с вашим проектом бетонных свай.!

Калькулятор проектирования фундамента

Ссылки

• • Требования Строительных норм для конструкционного бетона (2014). переменный ток! 318-14 Американский институт бетона.
  • Hsiao, J.K. (2012). Влияние оси изгиба на момент нагрузки (ВЕЧЕРА) Диаграммы взаимодействия круглых бетонных колонн с ограниченным количеством продольных арматурных стержней. Электронный журнал структурной инженерии 12 (1). Получено с http://www.ejse.org