Системы плит, рассматриваемые стандартом
Австралийские стандарты устанавливают минимальные требования к конструкции железобетонных плит., такие как односторонние и двусторонние типы. Относительно конфигурации плана и включения балок, плиты также можно разделить на плиты, поддерживаемые с четырех сторон, балочно-плитные системы, плоские плиты, и плоские пластины. Эти типы представлены на следующих изображениях..
Упростите соответствие конструкции австралийских плит с помощью передовых технологий SkyCiv. Экспорт подробного отчета о расчетах для использования в качестве конечного результата или в пакете расчетов.. Попробуйте это! Легко применять AS 3600 проверки слябов и плоских плит.
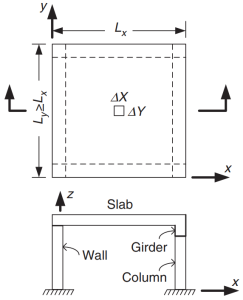
фигура 1. Плита, поддерживаемая с четырех сторон. (Ю-Чае Лу & Сануал Хуг Чоудхури , “Железобетон и предварительно напряженный бетон”, 2второе издание, Издательство Кембриджского университета).
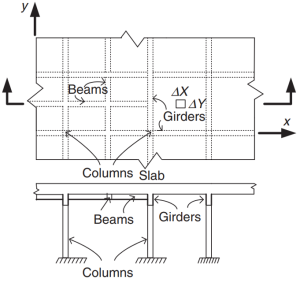
фигура 2. Система перекрытий ростверка. (Ю-Чае Лу & Сануал Хуг Чоудхури , “Железобетон и предварительно напряженный бетон”, 2второе издание, Издательство Кембриджского университета).
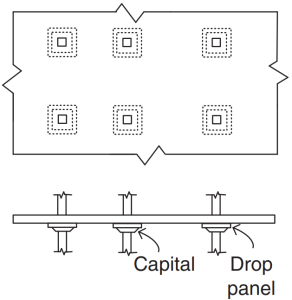
фигура 3. Плоские плиты. (Ю-Чае Лу & Сануал Хуг Чоудхури , “Железобетон и предварительно напряженный бетон”, 2второе издание, Издательство Кембриджского университета).
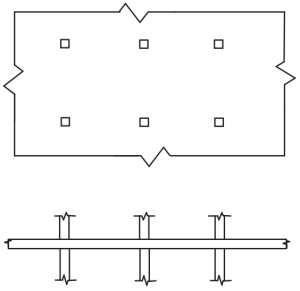
фигура 4. Плоские пластины. (Ю-Чае Лу & Сануал Хуг Чоудхури , “Железобетон и предварительно напряженный бетон”, 2второе издание, Издательство Кембриджского университета).
Стандарт рекомендует некоторые методы (упрощенные и проверенные процедуры) при определении изгибающих моментов:
- Пункт 6.10.2: Сплошные балки и односторонние плиты
- Пункт 6.10.3: Двусторонние плиты, поддерживаемые с четырех сторон
- Пункт 6.10.4: Двусторонние плиты с несколькими пролетами
Целью нормы является расчет общего количества стальной арматуры по основным направлениям в системе плит.. Арматура будет рассчитана на изгибающие моменты. “Mx” и “Мой.” фигура 5 показывает другие силы или действия в конечном элементе плиты, в котором код предписывает значения их сопротивления..
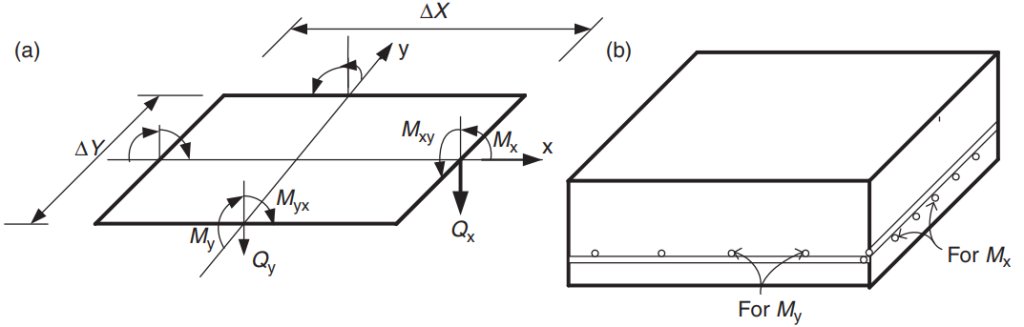
фигура 5. Силы в конечном элементе плиты: изгибающие моменты (Mx, Мой), крутящие моменты (Мкси, Микс), и ножницы (Кх, Qy). (Ю-Чае Лу & Сануал Хуг Чоудхури , “Железобетон и предварительно напряженный бетон”, 2второе издание, Издательство Кембриджского университета)
В этой статье, мы разработаем два примера проектирования плит, односторонние и двусторонние системы перекрытий, используя упрощенные методы, ориентированные и разрешенные кодом. В обоих случаях, мы создадим S3D-модель SkyCiv и сравним результаты с методами, упомянутыми выше..
Если вы новичок в SkyCiv, Зарегистрируйтесь и протестируйте программу самостоятельно!
Пример конструкции односторонней плиты
Ниже показано небольшое здание и плиты, которые мы спроектируем.
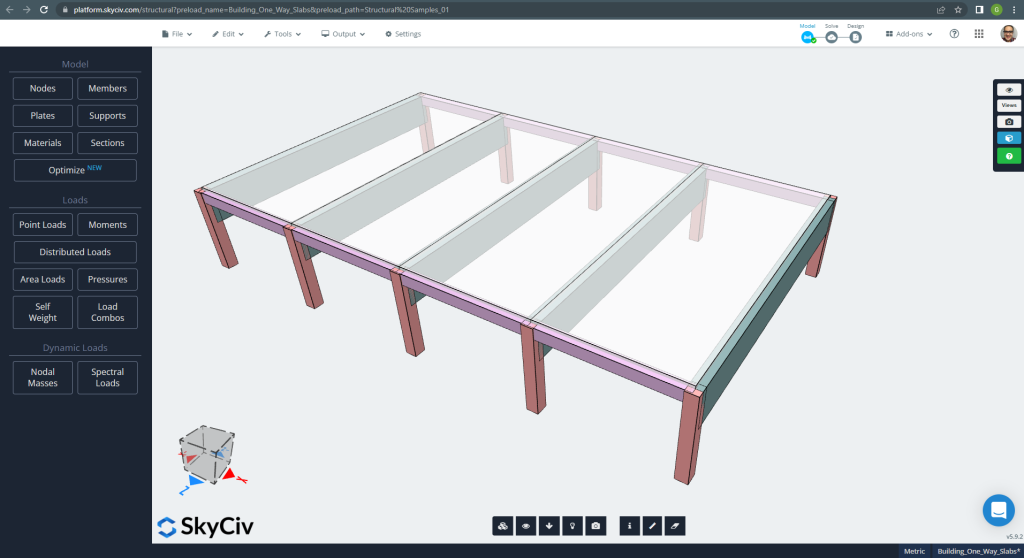
фигура 6. Односторонние плиты в примере небольшого здания. (Структурное 3D, Облачная инженерия SkyCiv).
Размеры плана показаны ниже.
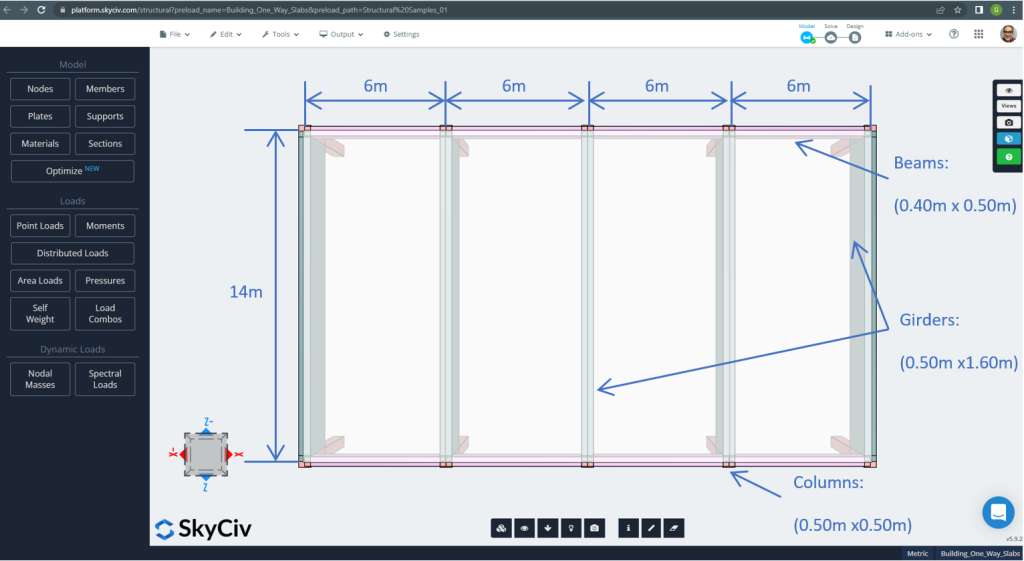
фигура 7. Размеры плана и конструктивные элементы. (Структурное 3D, Облачная инженерия SkyCiv).
Для примера плиты, В итоге, материал, свойства элементов, и множество для рассмотрения :
- Классификация типов плит: Один – способ поведения \(\гидроразрыва{Л_2}{Л_1} > 2 ; \гидроразрыва{14м}{6м}=2,33 > 2.00 \) Ok!
- Оккупация здания: Жилое использование
- Толщина плиты \(т_{плита}=0.25m\)
- Плотность железобетона при коэффициенте стального армирования 0.5% \(\ро_в = 24 \гидроразрыва{кН}{м^3} + 0.6 \гидроразрыва{кН}{м^3} \раз 0.5 знак равно 24.3 \гидроразрыва{кН}{м^3} \)
- Характеристическая прочность бетона на сжатие при 28 дней \(ф’к = 25 МПа \)
- Модуль упругости бетона по австралийскому стандарту \(Е_с = 26700 МПа \)
- Собственный вес плиты \(Dead = \rho_w \times t_{плита} знак равно 24.3 \гидроразрыва{кН}{м^3} \умножить на 0,25 м = 6.075 \гидроразрыва {кН}{м^2}\)
- Сверхналоженная статическая нагрузка \(SD = 3.0 \гидроразрыва {кН}{м^2}\)
- Живая нагрузка \(L = 2.0 \гидроразрыва {кН}{м^2}\)
Ручной расчет по стандарту AS3600
В этой секции, мы рассчитаем необходимую армированную стальную арматуру, используя ссылку на австралийский стандарт.. Сначала получим суммарный изгибающий момент, который должен воспринимать полоса плиты единичной ширины..
- Статическая нагрузка, \(г = (3.0 + 6.075) \гидроразрыва{кН}{м^2} \раз 1 m = 9.075 \гидроразрыва{кН}{м}\)
- Живая нагрузка, \(q = (2.0) \гидроразрыва{кН}{м^2} \раз 1 m = 2.0 \гидроразрыва{кН}{м}\)
- Предельная нагрузка, \(Fd = 1.2\times g + 1.5\раз q = (1.2\раз 9.075 + 1.5\раз 2.0)\гидроразрыва{кН}{м} =13.89 \frac{кН}{м} \)
Используя упрощенный метод, предусмотренный стандартом, первый, необходимо соблюдать следующие ограничения:
- \(\гидроразрыва{Л_и}{Л_дж} \в 1.2 . \гидроразрыва{6м}{6м} Ниже приведены различные способы определения коэффициентов давления грунта для расчета удельного сопротивления трения свай в песке. < 1.2 \). Ok!
- Нагрузка должна быть равномерной. Ok!
- \(q \le 2g. q=2 \frac{кН}{м} < 18.15 \гидроразрыва{кН}{м}\). Ok!
- Сечение плиты должно быть равномерным.. Ok!.
Рекомендуемая минимальная толщина, d
\(d \ge \frac{L_{фе}}{{к_3}{к_4}{\SQRT[3]{\гидроразрыва{\гидроразрыва{\Дельта}{L_{ef}}{Э_с}}{F_{d, ef}}}}}\)
куда
- \(к_3 = 1.0; к_4 = 1.75 \)
- \(\гидроразрыва{\Дельта}{L_{ef}}=1/250 \)
- \(Е_с = 27600 МПа \)
- \(F_{d,ef} знак равно (1.0 +к_{cs})\раз г + (\psi_s + к_{cs}\times \psi_1) \раз q=(1.0+0.8)\раз 9.075 + (0.7+0.8\раз 0.4)\раз 2 знак равно 18.375 kPa\)
- \(\psi_s = 0.7 \) Кратковременный коэффициент динамической нагрузки
- \(\psi_1 = 0.4 \) Долгосрочный коэффициент постоянной нагрузки
- \(к_{cs} знак равно 0.8 \)
\(d \ge \frac{5.50м}{{1.0}\раз {1.75}{\SQRT[3]{\гидроразрыва{\гидроразрыва{1}{250}\раз{27600 \раз 10^3 кПа}}{18.375 кПа}}}} \0,173 м. д = 0,25 м > 0.173м \) Ok!
Как только мы продемонстрируем, что ограничения удовлетворены, изгибающий момент рассчитывается по выражению: \(M=\alpha \times F_d \times L_n^2\) где \(\альфа) — константа, определенная на следующем рисунке.
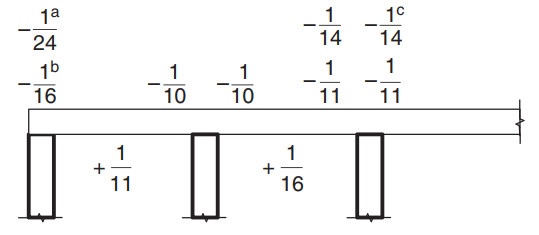
фигура 8. Значения моментного коэффициента \(\альфа) для плит с числом пролетов более двух. (Ю-Чае Лу & Сануал Хуг Чоудхури , “Железобетон и предварительно напряженный бетон”, 2второе издание, Издательство Кембриджского университета).
куда:
- (а ) Случай плит и балок на балочной опоре
- (б) Только для непрерывной балочной поддержки
- (с) Где используется арматура класса L
- \(Л_н \) - унитарный пролет полосы
- \(Ф_д \) гравитационная нагрузка
Для примера плиты, нам нужно использовать случай (а ) потому что плита опирается на жесткие балки. Будет объяснен только один случай, а остальные показаны в следующей таблице.. Мы также включаем расчет площади стальной арматуры..
- \(М={\альфа} {Ф_д}{Л_н^2}знак равно{-\гидроразрыва{1}{24}}\раз {13.89 \гидроразрыва{кН}{м}}\раз (6м-0.5м)^ 2 = – 17.51{кН}{м}\)
- Крышка = 20 мм (Минимум 10 мм необходим для периода огнестойкости. 60 минут).
- \(д = т_{плита} – Крышка – \гидроразрыва{БарДиаметр}{2} = 250 мм – 20мм – 6мм = 224 мм \)
- \(\альфа_2 = 1.0-0.003 f’c = 1.0-0.003\times 25 знак равно 0.925 (0.67 \le \alpha_2 \le 0.85) \) таким образом, мы выбираем \(\альфа_2 = 0.85\)
- \(\xi = \frac{\alpha_2\times f’c}{f_{его}} = frac{0.85\раз 25 МПа}{500 МПа} знак равно 0.0425 \)
- \(\rho_t = \xi – \SQRT{{\xi}^ 2 – \гидроразрыва{{2}{\xi}{M}}{{\фи}{б}{д ^ 2}{f_{его}}}} знак равно 0.0425 – \SQRT{{0.0425}^2-\frac{2\times 0.0425\times 17.51{кН}{м}}{{0.8}\раз {1м}\раз {{(0.224м)^ 2}} \раз {500\раз {10^3}кПа}}}=0.0008814\)
- \(\гамма= 1.05-0.007 f’c = 1.05-0.007\times 25 знак равно 0.875 (0.67 \le \gamma \le 0.85) \) таким образом, мы выбираем \(\гамма = 0.85\)
- \(k_u = \frac{\rho_t \times f_{его}}{0.85\times \gamma \times f’c}= Гидроразрыва{0.0008814\раз 500 МПа}{0.85\раз 0.85 \раз 25 МПа} =0.0244\)
- \(\фи = 1.19 – \гидроразрыва{13\раз k_{ты0}}{12} знак равно 1.19 – \гидроразрыва{13\раз 0.0244}{12} знак равно 1.164 (0.6 \le \phi \le 0.8) \) таким образом, мы выбираем \(\фи = 0.8\). Ok!.
- \(\расстояние от центра колонны{T,мин} знак равно 0.20 {(\гидроразрыва{D}{d})^ 2}{(\гидроразрыва{f'_{ct,е}}{f_{его}})} знак равно 0.20 \раз (\гидроразрыва{0.25м}{0.224м})^2 \times \frac{0.6\раз sqrt{25МПа}}{500 МПа} знак равно 0.0015\)
- \(A_{улица}=макс.(\расстояние от центра колонны{T,мин}, \ро_т)\times b \times d = max(0.0015,0.0008814)\раз 1000 mm \times 224 мм = 334.82 мм^2 \)
| \(\альфа) и моменты | Внешний негатив слева | Внешний Положительный | Внешний негатив справа | Внутреннее негативное левое | Интерьер Позитив | Внутреннее отрицательное право |
|---|---|---|---|---|---|---|
| \(\альфа) стоимость | -\(\гидроразрыва{1}{24}\) | \(\гидроразрыва{1}{11}\) | -\(\гидроразрыва{1}{10}\) | \(\гидроразрыва{1}{10}\) | \(\гидроразрыва{1}{16}\) | \(\гидроразрыва{1}{11}\) |
| значение М | -17.51 | 38.20 | -42.02 | 42.02 | 26.26 | 38.20 |
| \(\rho_t\) | 0.0008814 | 0.001948 | 0.002148 | 0.002148 | 0.00133 | 0.001948 |
| к | 0.0244 | 0.0539 | 0.0594 | 0.0594 | 0.0368 | 0.05391 |
| \(\фи) | 0.8 | 0.8 | 0.8 | 0.8 | 0.8 | 0.8 |
| \(A_{улица} {мм^2}\) | 334.82 | 436.31 | 481.099 | 481.099 | 334.8214 | 436.3100 |
После расчета площади стальной арматуры, вы можете определить детализацию (реальный способ размещения арматуры в плите). В помощь вашему знанию, мы делимся следующим изображением, который указывает расположение арматуры для положительных и отрицательных моментов:
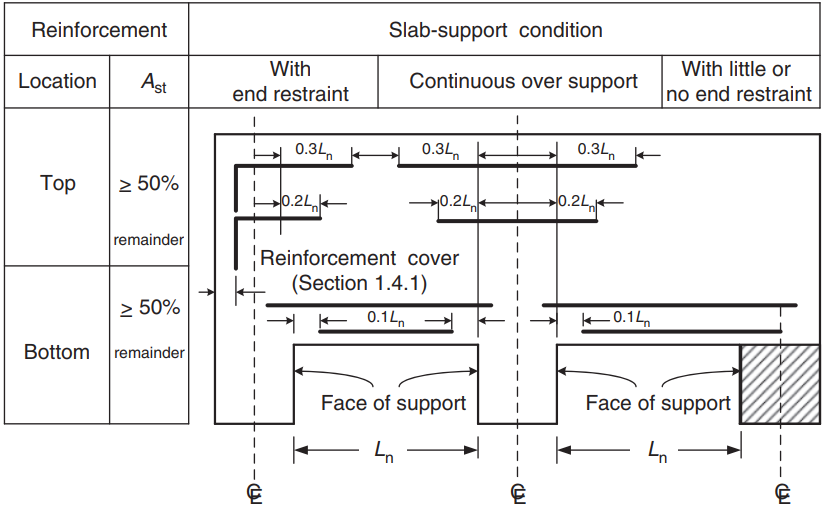
фигура 9. Схема армирования односторонних и двусторонних плит.. (Ю-Чае Лу & Сануал Хуг Чоудхури , “Железобетон и предварительно напряженный бетон”, 2второе издание, Издательство Кембриджского университета)
Если вы новичок в SkyCiv, Зарегистрируйтесь и протестируйте программу самостоятельно!
Результаты модуля проектирования пластин SkyCiv S3D
В первом представлении, мы покажем несколько изображений для моделирования и структурного анализа примера в S3D. Рекомендуем прочитать о моделировании в SkyCiv по следующим ссылкам. Как моделировать тарелки? - Коэффициент неравномерного конца по оси Z Пример проектирования плиты ACI с помощью SkyCiv.
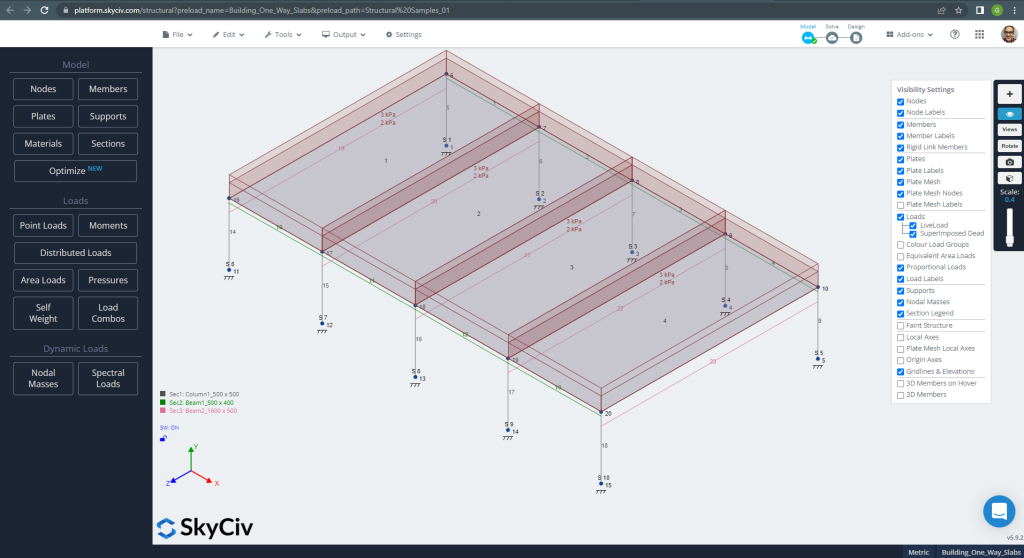
фигура 10. Структурная модель в S3D для примера односторонних плит. (Структурное 3D, Облачная инженерия SkyCiv).
Перед анализом модели, мы должны определить размер сетки пластины. Некоторые ссылки (2) порекомендуйте размер для элемента оболочки 1/6 короткого пролета или 1/8 длинного пролета, короче из них. После этого значения, у нас есть \(\гидроразрыва{L2}{6}= Гидроразрыва{6м}{6} = 1 м \) или \(\гидроразрыва{L1}{8}= Гидроразрыва{14м}{8}=1,75 м \); мы берем 1 м в качестве максимального рекомендуемого размера и применяемый размер ячейки 0,50 м.
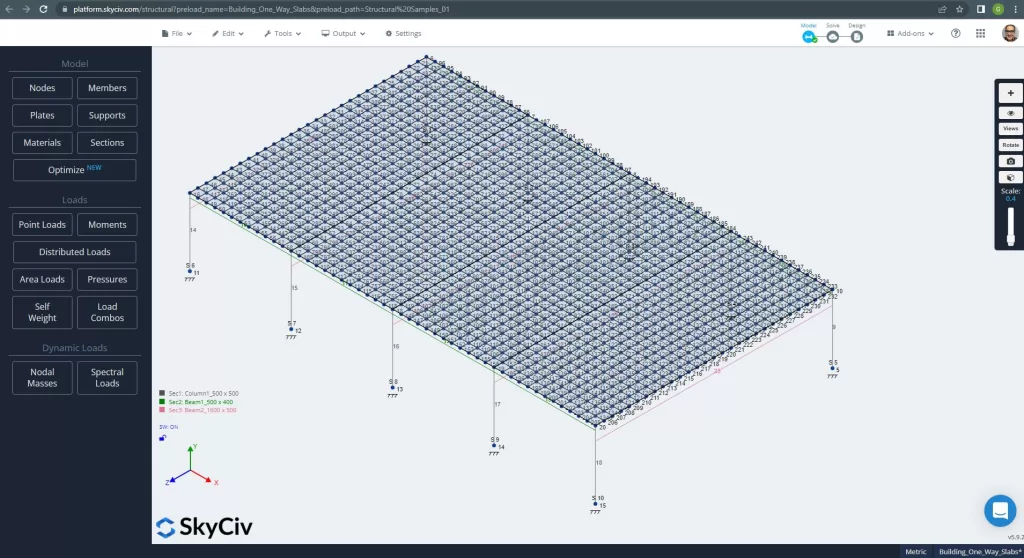
фигура 11. Улучшенная сетка в пластинах. (Структурное 3D, Облачная инженерия SkyCiv).
Как только мы улучшили нашу аналитическую структурную модель, мы проводим линейный упругий анализ. При проектировании плит, мы должны проверить, меньше ли вертикальное смещение, чем максимально допустимое кодом. Австралийскими стандартами установлено максимальное вертикальное смещение работоспособности \(\гидроразрыва{L}{250}= Гидроразрыва{6000мм}{250}=24.0 mm\).
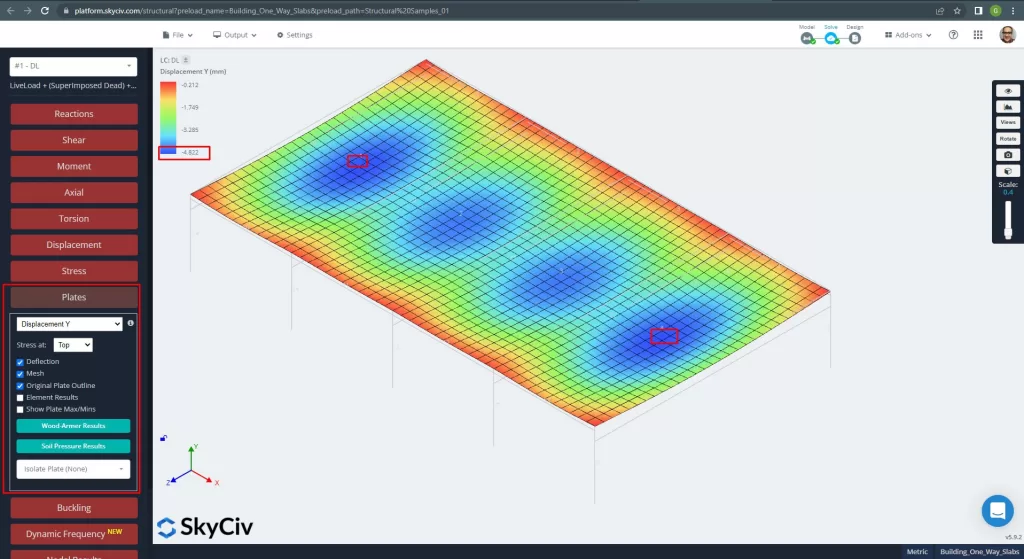
фигура 12. Вертикальное смещение в пластинах. (Структурное 3D, Облачная инженерия SkyCiv).
Сравнение максимального вертикального смещения со значением, указанным в коде., жесткость плиты достаточная. \(4.822 мм < 24.00mm\).
Максимальные моменты в пролетах плиты располагаются для положительных в центре и для отрицательных на внешних и внутренних опорах.. Давайте посмотрим значения этих моментов на следующих изображениях..
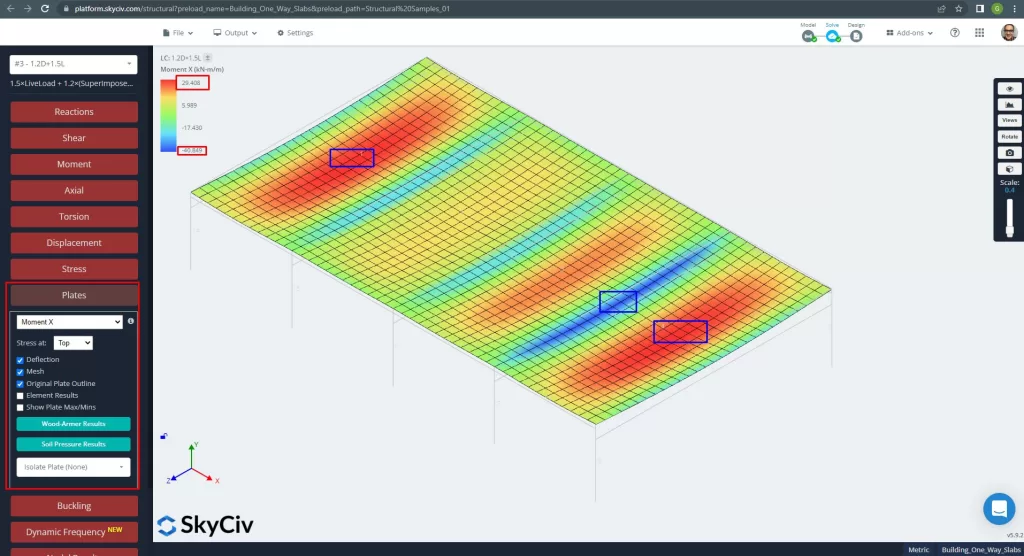
фигура 13. Моменты в направлении X. (Структурное 3D, Облачная инженерия SkyCiv).
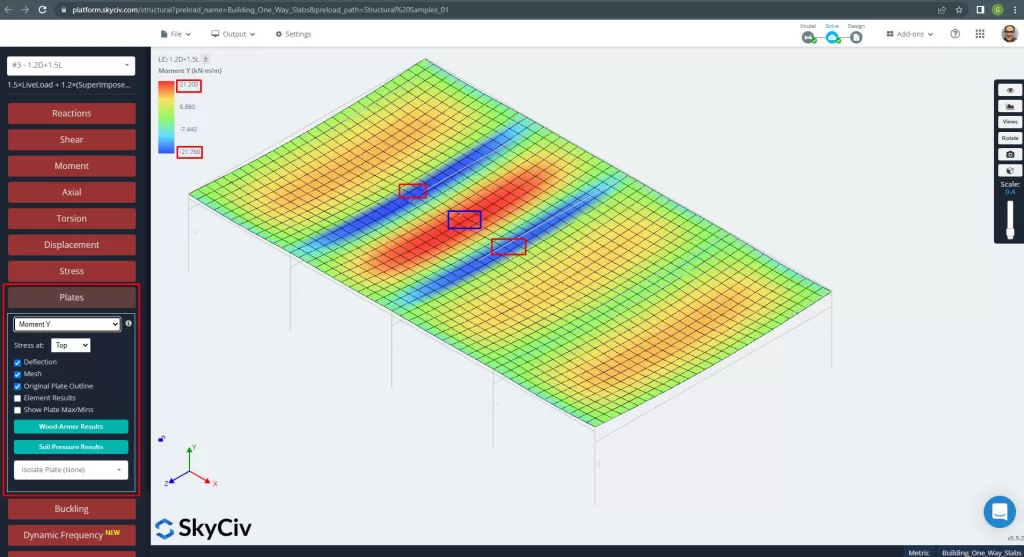
фигура 14. Моменты в направлении Y. (Структурное 3D, Облачная инженерия SkyCiv).
Местные оси пластинчатого элемента указаны ниже..
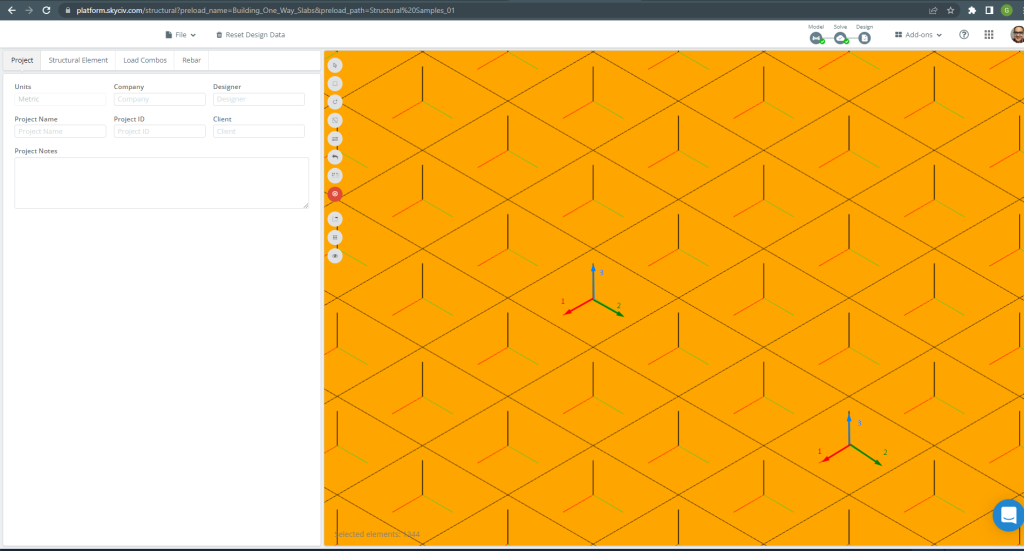
фигура 15. Местные оси плиты. (Структурное 3D, Облачная инженерия SkyCiv).
Более подробную информацию об автоматизированном проектировании армированных плит см., см. нашу документацию Тарелки в SkyCiv.
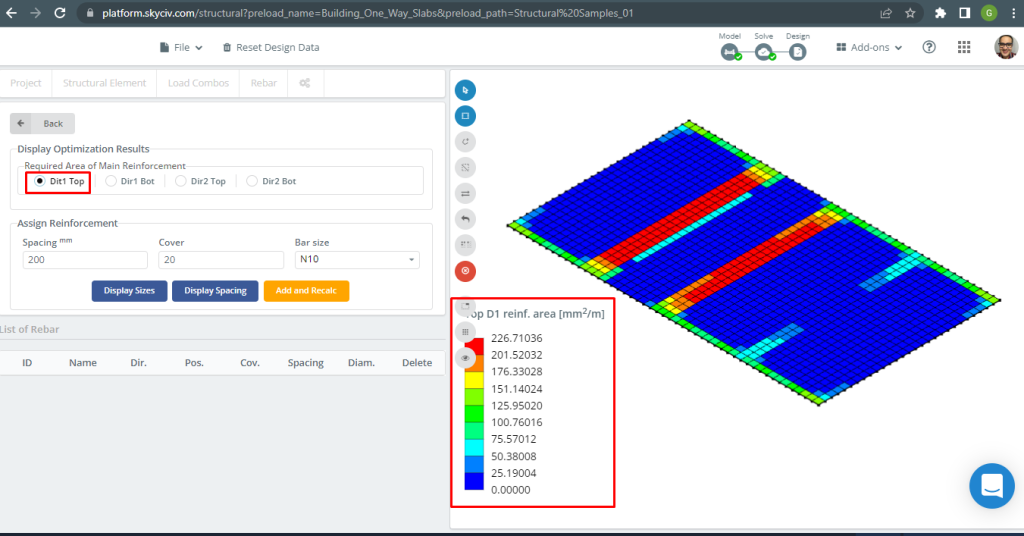
фигура 16. Верхнее армирование D1. (Структурное 3D, Облачная инженерия SkyCiv).
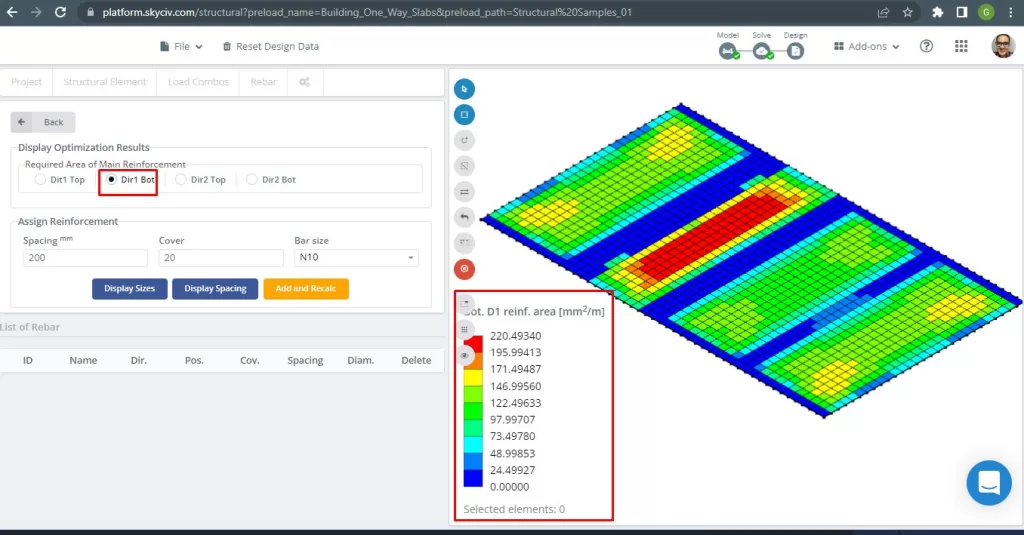
фигура 17. Нижнее усиление D1. (Структурное 3D, Облачная инженерия SkyCiv).
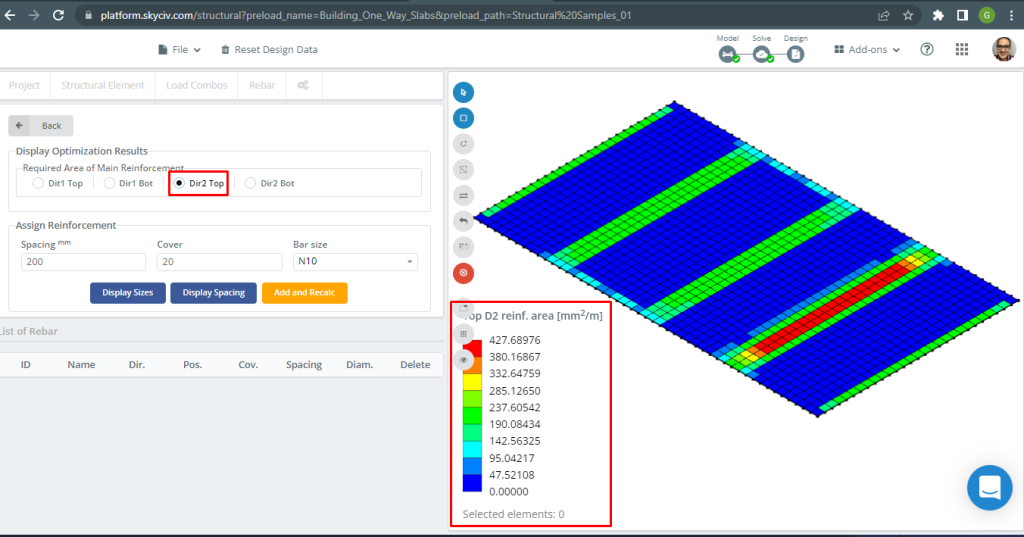
фигура 18. Верхнее армирование D2. (Структурное 3D, Облачная инженерия SkyCiv).
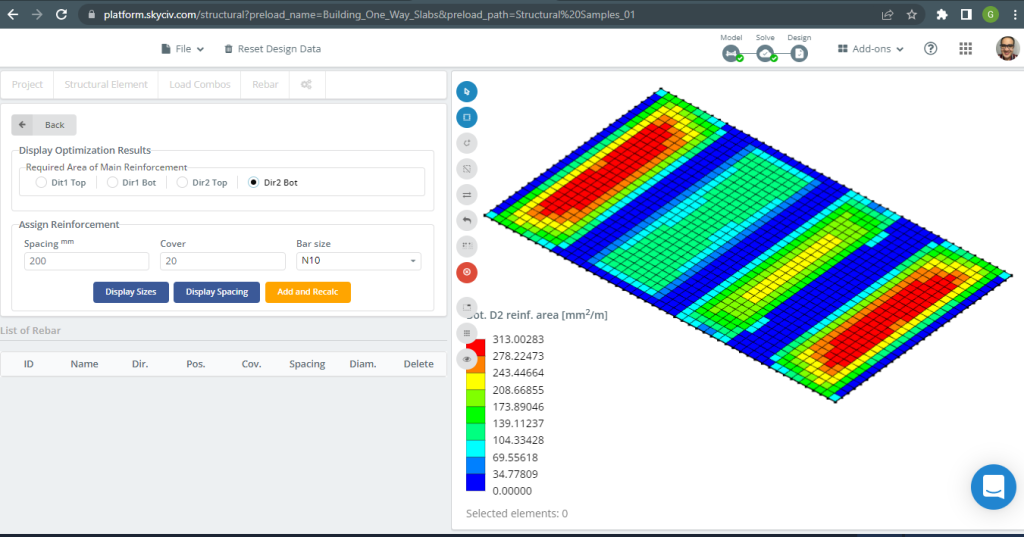
фигура 19. Нижнее усиление D2. (Структурное 3D, Облачная инженерия SkyCiv).
Сравнение результатов
Последним шагом в этом примере конструкции односторонней плиты является сравнение площади стальной арматуры, полученной с помощью анализа S3D. (местные оси “2”) и ручные расчеты.
| Моменты и площадь стали | Внешний негатив слева | Внешний Положительный | Внешний негатив справа | Внутреннее негативное левое | Интерьер Позитив | Внутреннее отрицательное право |
|---|---|---|---|---|---|---|
| \(A_{улица, HandCalcs} {мм^2}\) | 334.82 | 436.31 | 481.099 | 481.099 | 334.8214 | 436.3100 |
| \(A_{улица, S3D} {мм^2}\) | 285.13 | 313.00 | 427.69 | 427.69 | 313.00 | 427.69 |
| \(\Дельта_{диф}\) (%) | 14.84 | 28.262 | 11.101 | 11.101 | 6.517 | 1.986 |
Мы видим, что результаты значений очень близки друг к другу. значит расчеты верны!
Пример конструкции двусторонней плиты
В этой секции, разработаем пример, состоящий из ростверковой системы.
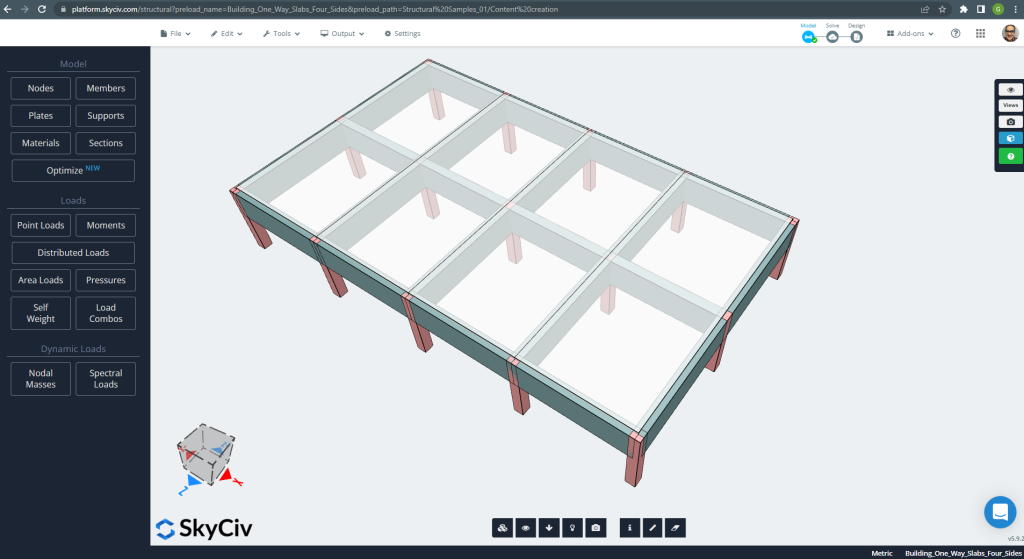
фигура 20. Система ростверка. (Структурное 3D, Облачная инженерия SkyCiv).
Размеры плана показаны ниже.
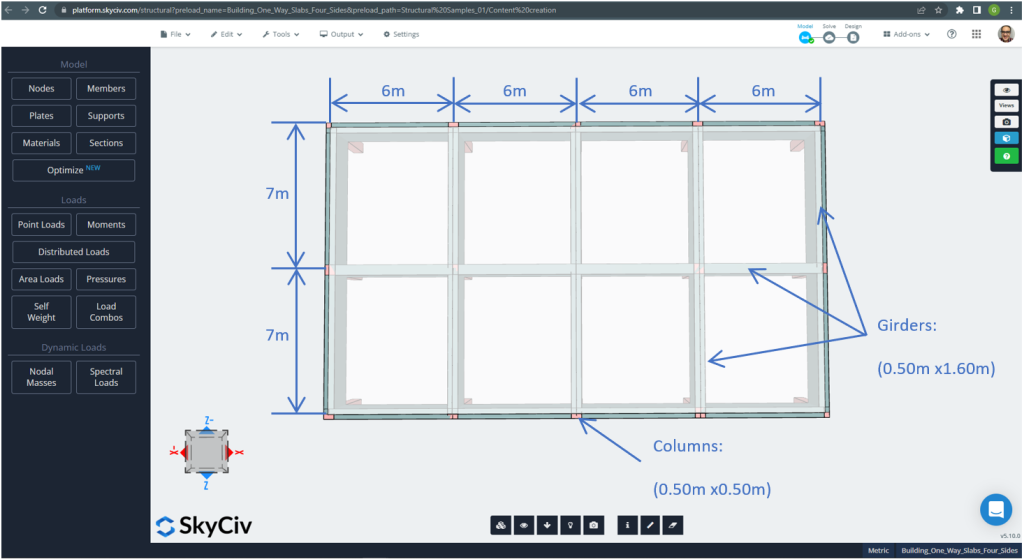
фигура 21. Размеры плана для примера четырехсторонней двусторонней плиты. (Структурное 3D, Облачная инженерия SkyCiv).
Для примера плиты, В итоге, материал, свойства элементов, и множество для рассмотрения :
- Классификация типов плит: Два – способ поведения \(\гидроразрыва{Л_2}{Л_1} \в 2 ; \гидроразрыва{7м}{6м}= 1,167 < 2.00 \) Ok!
- Оккупация здания: Жилое использование
- Толщина плиты \(т_{плита}=0.25m\)
- Плотность железобетона при коэффициенте стального армирования 0.5% \(\ро_в = 24 \гидроразрыва{кН}{м^3} + 0.6 \гидроразрыва{кН}{м^3} \раз 0.5 знак равно 24.3 \гидроразрыва{кН}{м^3} \)
- Характеристическая прочность бетона на сжатие при 28 дней \(ф’к = 25 МПа \)
- Модуль упругости бетона по австралийскому стандарту \(Е_с = 26700 МПа \)
- Собственный вес плиты \(Dead = \rho_w \times t_{плита} знак равно 24.3 \гидроразрыва{кН}{м^3} \умножить на 0,25 м = 6.075 \гидроразрыва {кН}{м^2}\)
- Сверхналоженная статическая нагрузка \(SD = 3.0 \гидроразрыва {кН}{м^2}\)
- Живая нагрузка \(L = 2.0 \гидроразрыва {кН}{м^2}\)
Ручной расчет по стандарту AS3600
В этой секции, мы рассчитаем необходимую армированную стальную арматуру, используя ссылку на австралийский стандарт.. Сначала мы получаем общий учтенный изгибающий момент, который будут переносить полосы единой ширины плиты в каждом главном направлении изгиба..
- Статическая нагрузка, \(г = (3.0 + 6.075) \гидроразрыва{кН}{м^2} \раз 1 m = 9.075 \гидроразрыва{кН}{м}\)
- Живая нагрузка, \(q = (2.0) \гидроразрыва{кН}{м^2} \раз 1 m = 2.0 \гидроразрыва{кН}{м}\)
- Предельная нагрузка, \(Fd = 1.2\times g + 1.5\раз q = (1.2\раз 9.075 + 1.5\раз 2.0)\гидроразрыва{кН}{м} =13.89 \frac{кН}{м} \)
Расчетные моменты и коэффициенты
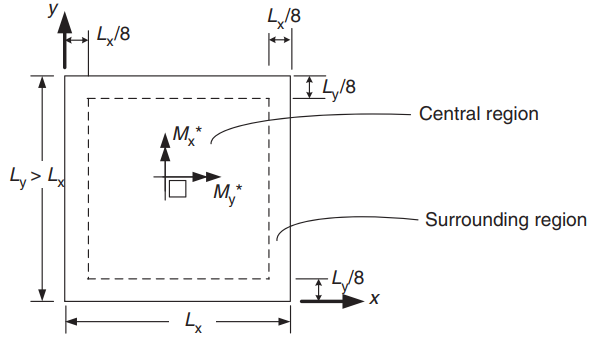
фигура 22. Ориентация двусторонней плиты для определения положительных моментов. (Ю-Чае Лу & Сануал Хуг Чоудхури , “Железобетон и предварительно напряженный бетон”, 2второе издание, Издательство Кембриджского университета)
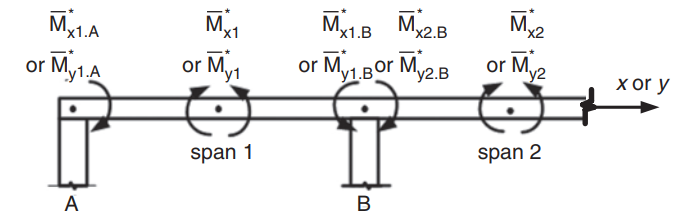
фигура 23. Определение отрицательных моментов в двусторонней плите. (Ю-Чае Лу & Сануал Хуг Чоудхури , “Железобетон и предварительно напряженный бетон”, 2второе издание, Издательство Кембриджского университета)
| Краевое состояние | Кратковременные коэффициенты (\(\beta_x\)) | Коэффициенты большого диапазона (\(\бета_y)\) все значения \(\гидроразрыва{Л_у}{Л_х}\) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Значения \(\гидроразрыва{Л_у}{Л_х}\) | |||||||||
| 1.0 | 1.1 | 1.2 | 1.3 | 1.4 | 1.5 | 1.75 | \(\гэ 2.0\) | ||
| 1. Четыре края непрерывные | 0.024 | 0.028 | 0.032 | 0.035 | 0.037 | 0.040 | 0.044 | 0.048 | 0.024 |
| 2. Один короткий край прерывается | 0.028 | 0.032 | 0.036 | 0.038 | 0.041 | 0.043 | 0.047 | 0.050 | 0.028 |
| 3. Один длинный край прерывистый | 0.028 | 0.035 | 0.041 | 0.046 | 0.050 | 0.054 | 0.061 | 0.066 | 0.028 |
| 4. Два коротких края прерывистые | 0.034 | 0.038 | 0.040 | 0.043 | 0.045 | 0.047 | 0.050 | 0.053 | 0.034 |
| 5. Два длинных края прерывистые | 0.034 | 0.046 | 0.056 | 0.065 | 0.072 | 0.078 | 0.091 | 0.100 | 0.034 |
| 6. Два смежных края прерывисты | 0.035 | 0.041 | 0.046 | 0.051 | 0.055 | 0.058 | 0.065 | 0.070 | 0.035 |
| 7. Три края прерывистые (один длинный край сплошной) | 0.043 | 0.049 | 0.053 | 0.057 | 0.061 | 0.064 | 0.069 | 0.074 | 0.043 |
| 8. Три края прерывистые (один короткий край сплошной) | 0.043 | 0.054 | 0.064 | 0.072 | 0.078 | 0.084 | 0.096 | 0.105 | 0.043 |
| 9. Четыре края разрываются | 0.056 | 0.066 | 0.074 | 0.081 | 0.087 | 0.093 | 0.103 | 0.111 | 0.056 |
Стол 1. (Ю-Чае Лу & Сануал Хуг Чоудхури , “Железобетон и предварительно напряженный бетон”, 2второе издание, Издательство Кембриджского университета)
На следующем изображении объясняются все девять случаев, к которым относится таблица выше.
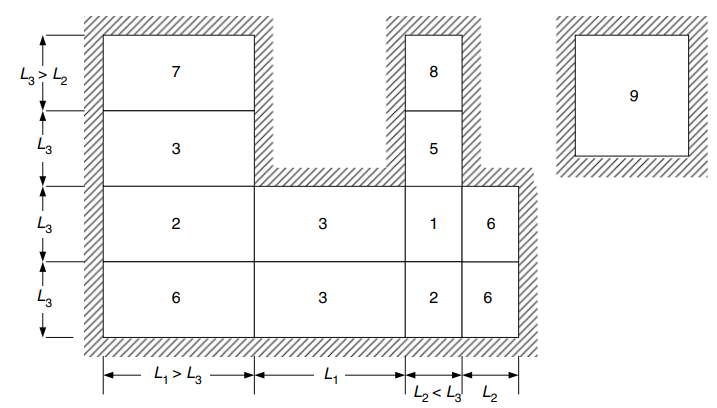
фигура 24. Краевые условия для двухсторонних плит, опертых с четырех сторон. (Ю-Чае Лу & Сануал Хуг Чоудхури , “Железобетон и предварительно напряженный бетон”, 2второе издание, Издательство Кембриджского университета)
Проектные моменты для центрального региона (Дело 6 Два смежных края прерывисты.) :
- \(L_x = 6м, L_y=7м, \гидроразрыва{Л_у}{Л_х} = frac{7м}{6м}знак равно 1.167 \) Значения для линейной интерполяции
- Позитивы:
- \(М_х = {\beta_x}{Ф_д}{Л_х^2} знак равно {0.04435}\раз {13.89 \гидроразрыва{кН}{м}}\раз{(6м)^ 2}=22.177 kNm\)
- \(М_у = {\бета_y}{Ф_д}{Л_х^2} знак равно{0.035}\раз {13.89 \гидроразрыва{кН}{м}}\раз{(6м)^ 2}=17,501 кНм \)
- Негативы внешнего пролета:
- \(M_{х1,А} = -\lambda_e \times M_x = -0.5 \раз 22.177 кНм = – 11.089 kNm\)
- \(M_{у1,А} = -\lambda_e \times M_y = -0.5 \раз 17.501 кНм = -8.751 кНм \)
- Негативы внутреннего пролета:
- \(M_{х1, Б} = -\lambda_{1Икс} \раз M_x = -1.33 \раз 22.177 кНм = – 29.495 kNm\)
- \(M_{у1, В} = -\lambda_{1и} \раз M_y = -1.33 \раз 17.501 кНм = -23.276 кНм \)
Проектные моменты для центрального региона (Дело 3 Один длинный край прерывистый) :
- \(L_x = 6м, L_y=7м, \гидроразрыва{Л_у}{Л_х} = frac{7м}{6м}знак равно 1.167 \) Значения для линейной интерполяции
- Позитивы:
- \(М_х = {\beta_x}{Ф_д}{Л_х^2} знак равно {0.03902}\раз {13.89 \гидроразрыва{кН}{м}}\раз{(6м)^ 2}знак равно 19.512 kNm\)
- \(М_у = {\бета_y}{Ф_д}{Л_х^2} знак равно{0.028}\раз {13.89 \гидроразрыва{кН}{м}}\раз{(6м)^ 2}знак равно 14.001 кНм \)
- Негативы внутреннего пролета:
- \(M_{х1, Б} = -\lambda_{1Икс} \раз M_x = -1.33 \раз 19.512 кНм = – 25.951 kNm\)
- \(M_{у1, Б} = -\lambda_{1и} \раз M_y = -1.33 \раз 14.001 кНм = – 18.621 кНм \)
- Негативы внутреннего второго пролета:
- \(M_{х2,Б} = -\lambda_{2Икс} \раз M_x = -1.33 \раз 19.512 кНм = – 25.951 kNm\)
- \(M_{у2,Б} = -\lambda_{2и} \раз M_y = -1.33 \раз 14.001 кНм = – 18.621 кНм \)
Арматура стальная для направления X
| \(\альфа) и моменты | Внешний негатив слева | Внешний Положительный | Внешний негатив справа | Внутреннее негативное левое | Интерьер Позитив | Внутреннее отрицательное право |
|---|---|---|---|---|---|---|
| значение М | 11.089 | 22.177 | 29.495 | 25.951 | 19.512 | 25.951 |
| \(\rho_t\) | 0.00055614 | 0.00112 | 0.001496 | 0.001313 | 0.000984 | 0.001313 |
| к | 0.015395 | 0.0310 | 0.0414 | 0.0364 | 0.0272 | 0.0364 |
| \(\фи) | 0.8 | 0.8 | 0.8 | 0.8 | 0.8 | 0.8 |
| \(A_{улица} {мм^2}\) | 334.8214 | 334.8214 | 335.08233 | 334.821 | 334.8214 | 334.8214 |
Арматурная сталь для направления Y
| \(\альфа) и моменты | Внешний негатив слева | Внешний Положительный | Внешний негатив справа | Внутреннее негативное левое | Интерьер Позитив | Внутреннее отрицательное право |
|---|---|---|---|---|---|---|
| значение М | 8.751 | 17.501 | 23.276 | 18.621 | 14.001 | 18.621 |
| \(\rho_t\) | 0.0004383 | 0.0008811 | 0.001176 | 0.0009381 | 0.000703 | 0.0009381 |
| к | 0.0121 | 0.0244 | 0.03256 | 0.02597 | 0.0195 | 0.02597 |
| \(\фи) | 0.8 | 0.8 | 0.8 | 0.8 | 0.8 | 0.8 |
| \(A_{улица} {мм^2}\) | 334.821 | 334.821 | 334.821 | 334.821 | 334.8214 | 334.821 |
Если вы новичок в SkyCiv, Зарегистрируйтесь и протестируйте программу самостоятельно!
Результаты модуля проектирования пластин SkyCiv S3D
После уточнения модели, пришло время провести линейный упругий анализ.
При проектировании плит, мы должны проверить, меньше ли вертикальное смещение, чем максимально допустимое кодом. Австралийскими стандартами установлено максимальное вертикальное смещение работоспособности \(\гидроразрыва{L}{250}= Гидроразрыва{6000мм}{250}=24.0 mm\).
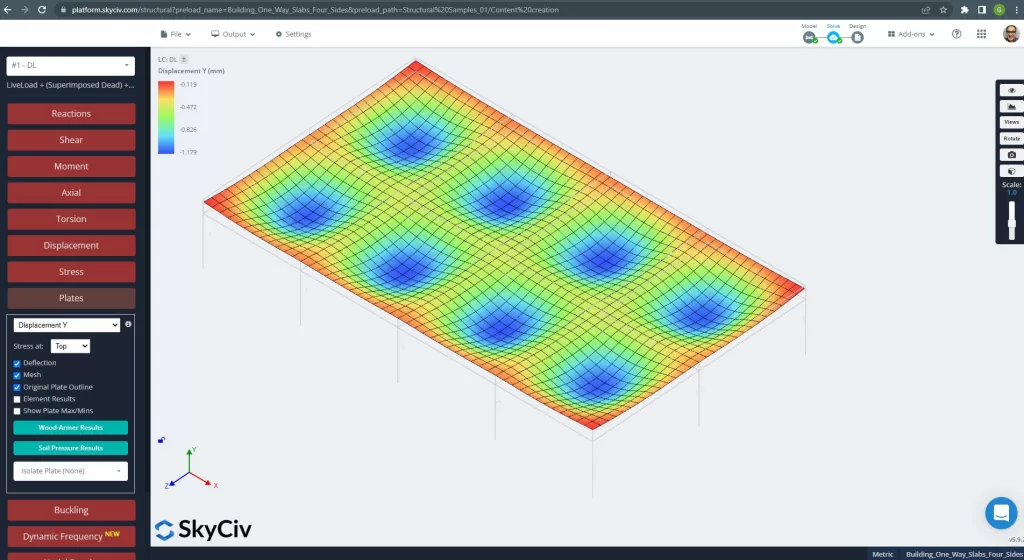
фигура 25. Вертикальное смещение в системе плит ростверка. (Структурное 3D, Облачная инженерия SkyCiv).
Изображение выше дает нам вертикальное смещение. Максимальное значение составляет -1,179 мм, что меньше максимально допустимого значения -24 мм.. Следовательно, жесткость плиты достаточная.
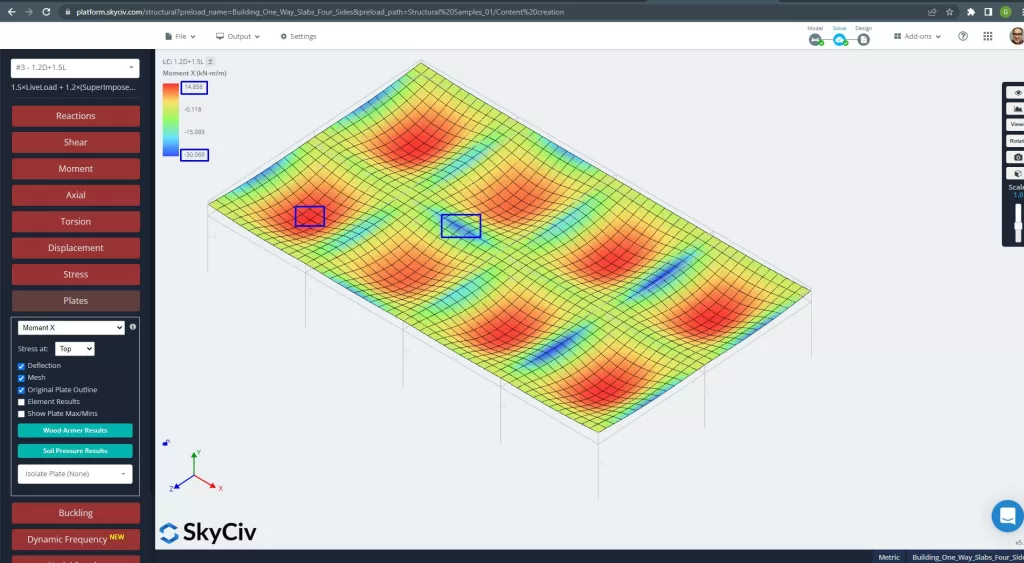
фигура 26. Моменты пластин в направлении X. (Структурное 3D, Облачная инженерия SkyCiv).
Изображений 27 и 28 состоит из изгибающего момента в каждом основном направлении. Получение распределения моментов и значений, программное обеспечение, SkyCiv, можно получить общую площадь стальной арматуры.
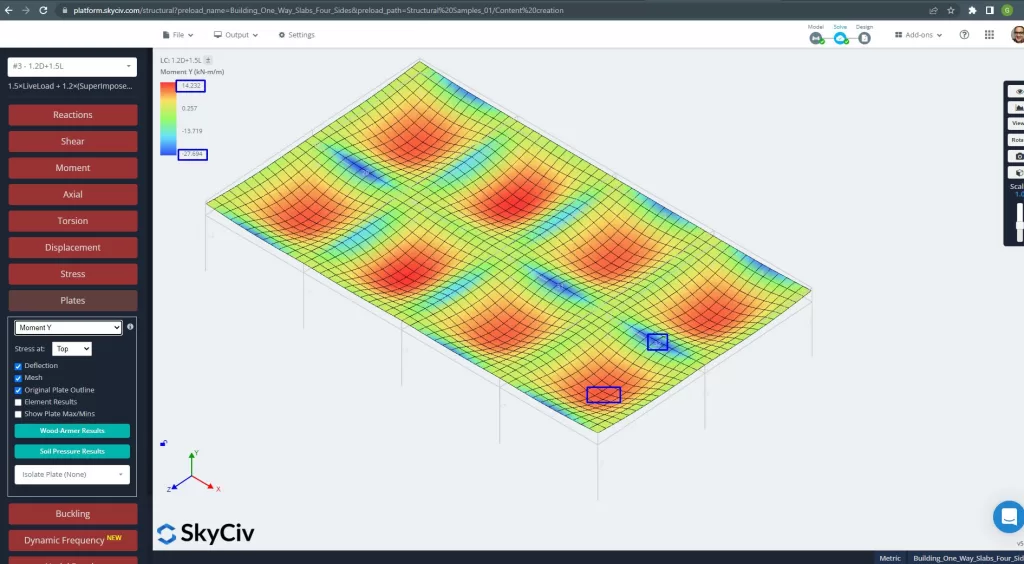
фигура 27. Моменты пластин в направлении Y. (Структурное 3D, Облачная инженерия SkyCiv).
Участки стального армирования:
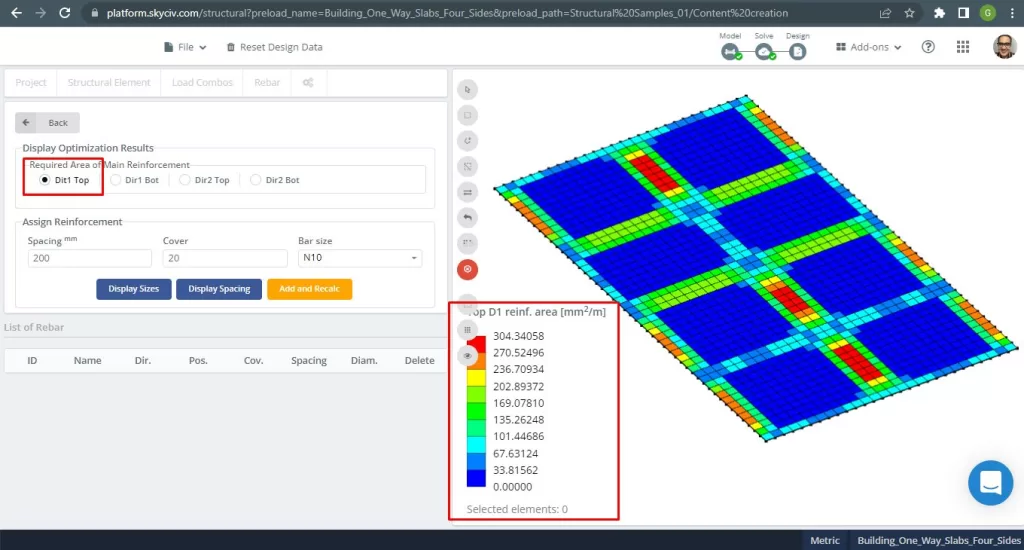
фигура 28. Верхнее армирование стальной арматуры в направлении 1. (Структурное 3D, Облачная инженерия SkyCiv).
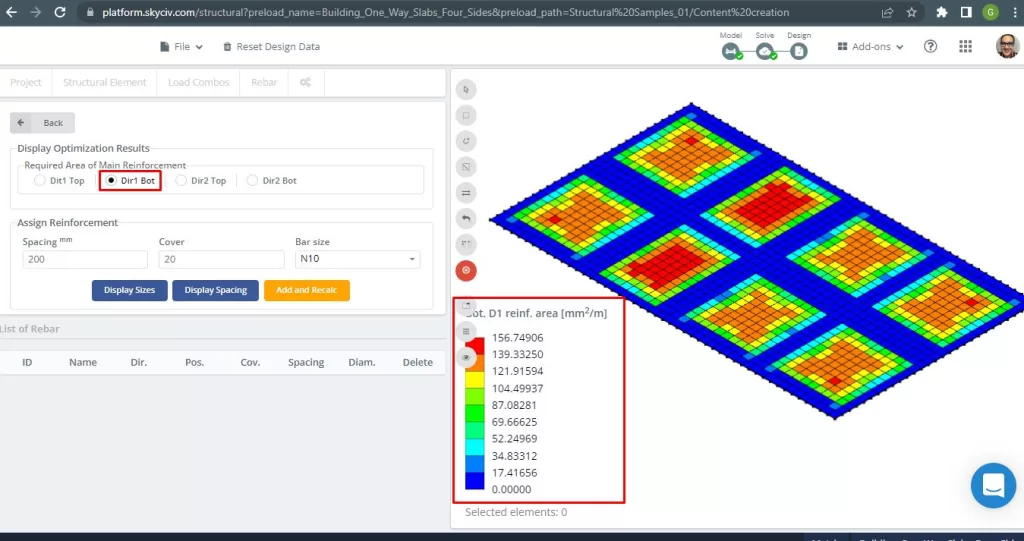
фигура 29. Нижняя стальная арматура, армированная в направлении 1. (Структурное 3D, Облачная инженерия SkyCiv).
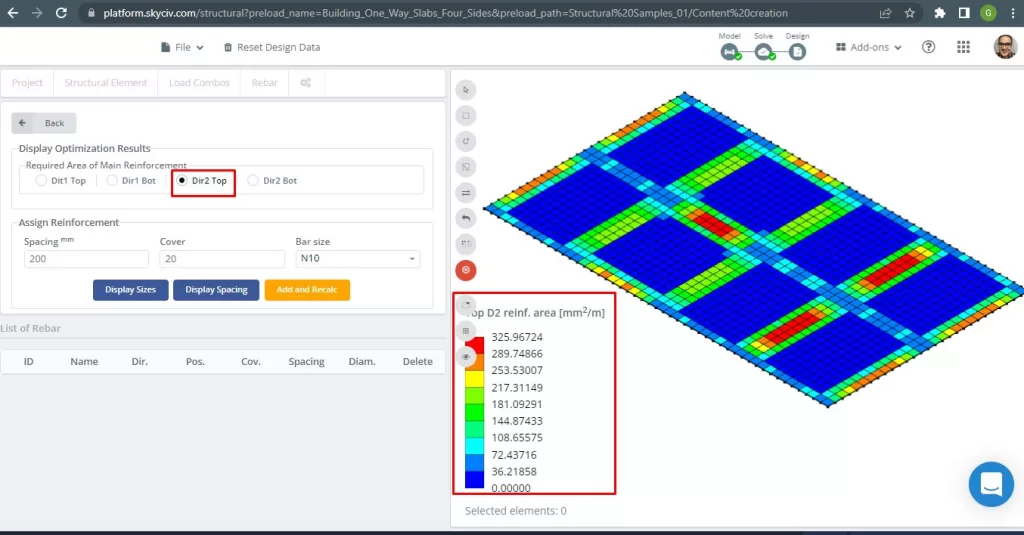
фигура 30. Верхнее армирование стальной арматуры в направлении 2. (Структурное 3D, Облачная инженерия SkyCiv).
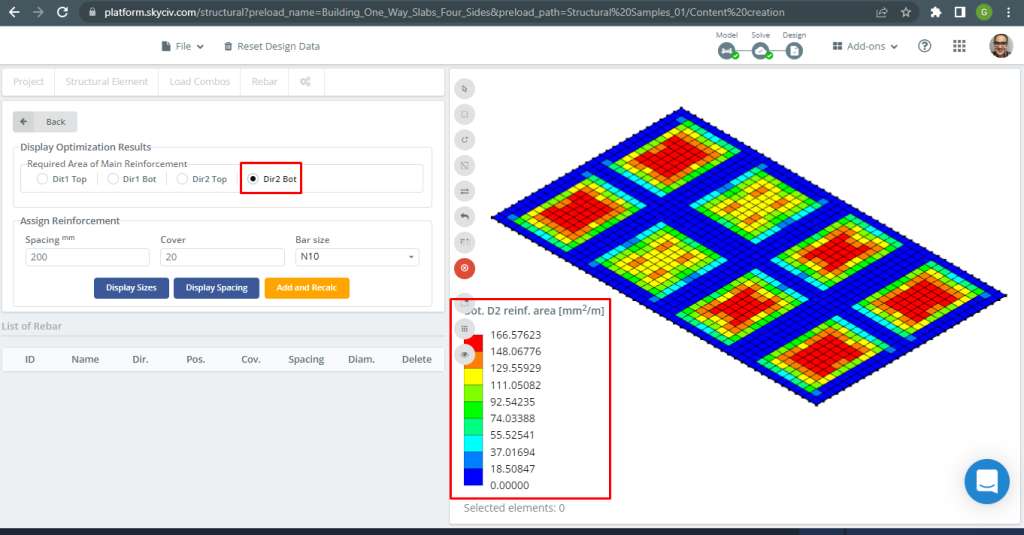
фигура 31. Нижняя стальная арматура, армированная в направлении 2. (Структурное 3D, Облачная инженерия SkyCiv).
Сравнение результатов
Последний шаг в этом примере проектирования односторонней плиты — сравнение площади стальной арматуры, полученной с помощью S3D-анализа и ручных расчетов..
Арматура стальная для направления X
| Моменты и площадь стали | Внешний негатив слева | Внешний Положительный | Внешний негатив справа | Внутреннее негативное левое | Интерьер Позитив | Внутреннее отрицательное право |
|---|---|---|---|---|---|---|
| \(A_{улица, HandCalcs} {мм^2}\) | 334.8214 | 334.8214 | 335.08233 | 334.821 | 334.8214 | 334.8214 |
| \(A_{улица, S3D} {мм^2}\) | 289.75 | 149.35 | 325.967 | 325.967 | 116.16 | 217.311 |
| \(\Дельта_{диф}\) (%) | 13.461 | 55.39 | 2.720 | 2.644 | 65.307 | 35.0964 |
Арматурная сталь для направления Y
| Моменты и площадь стали | Внешний негатив слева | Внешний Положительный | Внешний негатив справа | Внутреннее негативное левое | Интерьер Позитив | Внутреннее отрицательное право |
|---|---|---|---|---|---|---|
| \(A_{улица, HandCalcs} {мм^2}\) | 334.821 | 334.821 | 334.821 | 334.821 | 334.821 | 334.821 |
| \(A_{улица, S3D} {мм^2}\) | 270.524 | 156.75 | 304.34 | 304.34 | 156.75 | 270.52 |
| \(\Дельта_{диф}\) (%) | 19.203 | 53.184 | 9.104 | 9.104 | 53.184 | 19.204 |
Разница довольно велика для положительных моментов, и причиной может быть наличие балок с высокой жесткостью на кручение, которые влияют на результаты анализа методом конечных элементов пластины и расчеты на изгиб арматурной стали..
Если вы новичок в SkyCiv, Зарегистрируйтесь и протестируйте программу самостоятельно!
Ссылки
- Ю-Чае Лу & Сануал Хуг Чоудхури , “Железобетон и предварительно напряженный бетон”, 2второе издание, Издательство Кембриджского университета.
- Базан Энрике & Мели Пиралла, “Сейсмический расчет сооружений”, 1ред, ПРОЗРАЧНЫЙ.
- Австралийский стандарт, Бетонные конструкции, КАК 3600:2018


