What are P-Delta Effects?
Of course, any structural model will deflect when it is loaded. A deflected structure may encounter significant secondary moments because the ends of the members have changed position. To illustrate this, consider the simple cantilevered column example shown below: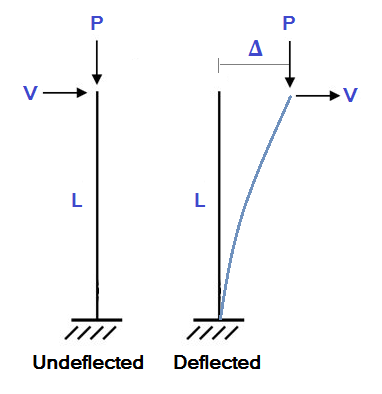
In this example, a column of length L is encountering an axial load (P) and a lateral load (V). In a standard linear static analysis we would calculate the lateral deflection (Δ) as:
[math]
\Delta = \dfrac{ML^2}{3EI} = \dfrac{VL^3}{3EI} \text{ since M=VL}
[math]
Notice that in the case of a linear static analysis the lateral deflection, Δ, depends on the lateral load (V). However, if the column is encountering an axial load (P), then wouldn't the column deflect even more? This is obvious because the axial load would induce a secondary moment with a value of P×Δ. To illustrate this, let's sum the moments about the base of the column:
[math]
\sum{M}=(V \times L) + (P \times \Delta)= VL + P\Delta \\\\
M_{1} = VL \\\\
M_{2} = P\Delta
[math]
Here M1 is due to the lateral point load whereas, M2 is due to the axial load. Each of these moments contribute to lateral deflection differently (you can look up the cantilever formulae for the end deflection due to a point load and a moment, respectively for these formulae):
[math]
\Delta_{1} = \dfrac{M_{1}L^2}{3EI} = \dfrac{VL^3}{3EI} \\\\
\Delta_{2} = \dfrac{M_{2}L^2}{2EI} = \dfrac{P \Delta L^2}{2EI}
[math]
So really, the total lateral deflection would be closer to:
[math]
\Delta_{new} = \Delta_{1} + \Delta_{2} = \dfrac{VL^3}{3EI} + \dfrac{P \Delta L^2}{2EI}
[math]
We can see that compared to the original deflection value, there is an extra term on the right in terms of P and Δ. If P or Δ are significant values, the standard linear static analysis would be underestimating the deflection of the column. It should be obvious now that a P-Delta Analysis is named after the secondary moment PΔ. Therefore, P-Delta effects are caused by geometric non-linearity. For this reason, a P-Delta Analysis is often called a Non-Linear Analysis. A proper P-Delta Analysis would continue to iterate the process above to update the value of Δnew.
When do I need to worry about conducting a P-Delta Analysis?
The good news is that SkyCiv Structural 3D can now perform a P-Delta Analysis for you. P-Delta effects usually become prevalent in tall structures that are experiencing gravity loads and lateral displacement due to wind or other forces. If the lateral displacement and/or the vertical axial loads through the structure are significant, a P-Delta Analysis should be performed to account for the non-linearities. In many cases, a linear static analysis can severely underestimate displacement (among other results) in comparison with a P-Delta (Non-Linear) Analysis. The importance of a P-Delta Non-Linear Analysis will be illustrated in the example below. The multi-storey frame of the building is 20m in height, with each storey being 5m high. The columns are fully fixed at the base with distributed loads on each level. Additionally, there are vertical loads on the top floor and self weight is considered so gravity loads can be simulated. There is also a relatively small lateral load applied to the side of the structure.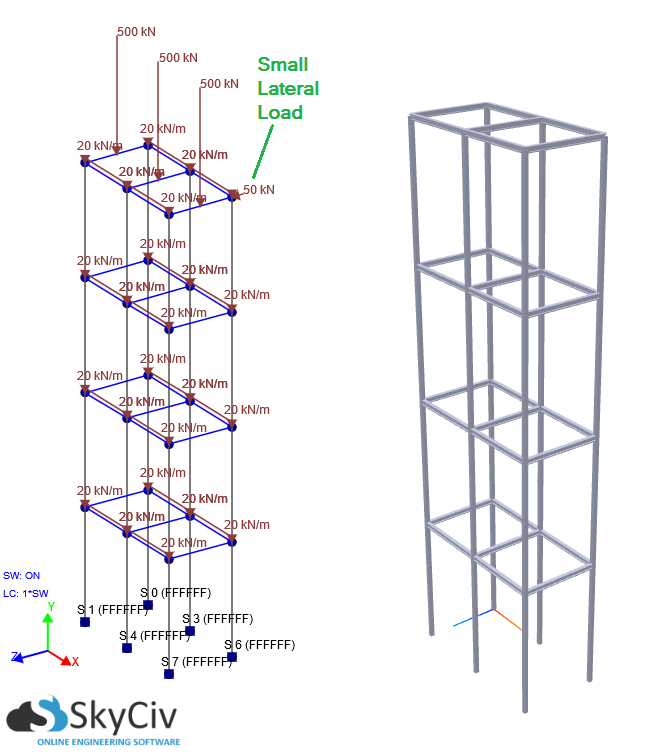
Under these conditions let's compare the results between a Linear and P-Delta (Non-Linear) Analysis:
| Linear | P-Delta (Non-Linear) | % Difference | |
|---|---|---|---|
| Max Total Displacement | 254 mm | 353 mm | + 39% |
| Max Vertical Reaction | 629 kN | 668 kN | + 6% |
| Max Moment Reaction | 42 kN-m | 60 kN-m | + 43% |
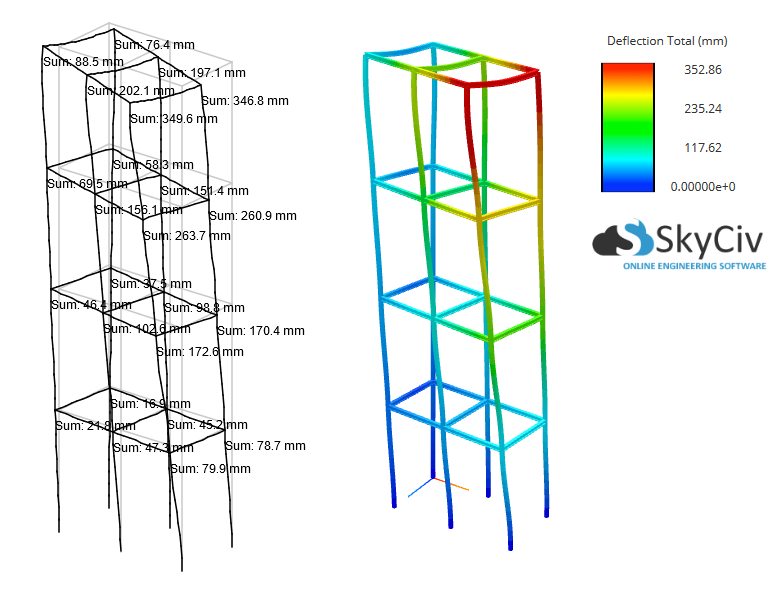It is clear that P-Delta effects play an extremely significant role with this structure, increasing the max deflection and max moment results by around 40%! Thus, a linear static analysis is inadequate in such a case.
In summary, P-Delta Analysis is preferable to Linear Static Analysis as it accounts for unforeseen non-linearities in your model. You can use SkyCiv Structural 3D to perform fast and effective P-Delta Analyses on your models; simply select "P-Delta Analysis" when clicking "Solve." Let the software do the work for you so all you have to worry about is the design!
Paul Comino
CTO and Co-Founder of SkyCiv
BEng Mechanical (Hons1), BCom
LinkedIn
CTO and Co-Founder of SkyCiv
BEng Mechanical (Hons1), BCom
