Kostenloser Trägheitsmoment- und Schwerpunktrechner
Berechnen Sie das Trägheitsmoment, Schwerpunkt, und Abschnittsmodul für eine Vielzahl von Formen
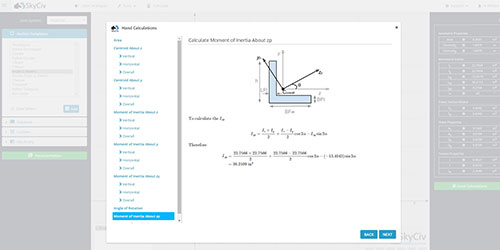
Ausführliche Anleitung zu unserem Trägheitsmomentrechner
Mit dem SkyCiv Trägheitsmoment- und Schwerpunkt-Rechner können Sie das Trägheitsmoment, den Schwerpunkt, und andere wichtige geometrische Eigenschaften für eine Vielzahl von Formen wie Rechtecke, Kreise, Hohlprofile, Dreiecke, I-Träger, T-Träger, Winkel und Kanäle bestimmen. Unten finden Sie auch einige Artikel über die Berechnung des Trägheitsmoments, und weitere Informationen über Schwerpunkt und Widerstandsmoment.
Sie können bis zu drei Abschnitte lösen, bevor Sie sich für ein kostenloses Benutzerkonto anmelden müssen - mit dem Sie Zugang zu mehr Software und Ergebnissen erhalten. Unser kostenpflichtiges Konto zeigt die vollständigen manuellen Berechnungen, wie das Tool zu diesem Ergebnis gekommen ist. Weitere Informationen zu diesem Thema sowie Links zu anderen nützlichen Tools und Funktionen, die SkyCiv Ihnen bietet, finden Sie unter dem Rechner.
So verwenden Sie den SkyCiv-Trägheitsmomentrechner
Sehen Sie sich das Demo-Video unten an, um mit unserem Rechner zu beginnen.
Wählen Sie einfach die Querschnittsform, die Sie berechnen möchten, aus der Dropdown-Liste aus, geben Sie die Abmessungen des ausgewählten Querschnitts ein und klicken Sie auf Berechnen.
Dieser kostenlose Mehrzweck-Rechner ist Teil unserer umfassenden Software zur Strukturanalyse. Der Rechner ermöglicht Ihnen:
- Berechnung des Trägheitsmoments (I) eines Trägerquerschnitts (zweites Flächenträgheitsmoment)
- Berechnen Sie den Schwerpunkt (C.) in der X- und Y-Achse eines Trägerquerschnitts
- Berechnung des ersten Flächenträgheitsmoments (Statisches Trägheitsmoment) (Q.) eines Trägerquerschnitts
- Querschnittsmodulrechner zur Berechnung des Querschnittsmoduls (MIT) eines Trägerquerschnitts
- Berechnung der Torsionskonstanten (J.) eines Trägerquerschnitts
Gemeinsame Abschnittseigenschaftsdefinitionen
Der Trägheitsmomentrechner berechnet eine Reihe wichtiger Querschnittseigenschaften, die im Bauwesen verwendet werden. Es folgt eine kurze Auflistung der Begriffe und Definitionen der Querschnittswerte:
- Querschnittsfläche (Ein) – Die Querschnittsfläche ist eine recht einfache Berechnung, die jedoch direkt für die Berechnung der axialen Spannung verwendet wird (je größer die Querschnittsfläche, desto höher die axiale Festigkeit)
- Trägheitsmoment (Iz, Iy) – auch bekannt als zweites Flächenträgheitsmoment, ist eine Berechnung zur Bestimmung der Festigkeit eines Bauteils und seines Widerstands gegen Durchbiegung. Je höher diese Zahl ist, desto stärker ist das Profil. Hier gibt es zwei Achsen:
- Hauptachse (Iz) – Sie verläuft um die Z-Achse und wird in der Regel als Hauptachse betrachtet, da sie in der Regel die stärkste Richtung des Trägers ist
- Neben achse (Iy) - Sie verläuft um die Y-Achse und gilt als Nebenachse oder schwache Achse. Der Grund dafür ist, dass die Profile nicht für die Aufnahme von so viel Kraft um diese Achse ausgelegt sind
- Wenn eine Form in beiden Richtungen die gleichen Abmessungen hat (quadratisch, kreisförmig usw..) sind diese Werte in beiden Richtungen identisch. Siehe Inerialmoment eines Kreises, um mehr darüber zu erfahren.
- Schwerpunkt (Cz, Cy) – dies ist der Schwerpunkt des Abschnitts und hat normalerweise eine Z- und Y-Komponente. Bei symmetrischen Formen, ist dies der geometrische Mittelpunkt. Bei nicht symmetrischen Formen (z.B. Winkel, Kanal) liegen diese an anderen Stellen. Erfahren Sie, wie Sie den Schwerpunkt eines Trägerprofils berechnen können. Der obige Rechner dient auch zur Berechnung des X- und Y-Schwerpunkts jeder Art von Form.
- Statisches Trägheitsmoment (Qz, Qy) – Auch bekannt als erstes Flächenmoment, misst es die Verteilung der Fläche eines Trägerprofils von einer Achse aus. Wie das Trägheitsmoment, gilt es sowohl für die Z- als auch für die Y-Richtung. Diese Werte werden in der Regel bei Berechnungen der Scherspannung verwendet, Je größer dieser Wert ist, desto stärker ist der Querschnitt gegen Scherung. Der Rechner liefert diesen Wert, aber klicken Sie hier, um mehr über die Berechnung des ersten Flächenmoments zu erfahren.
- Elastischer Querschnittsmodul (Sz, Sy in Amerika. Zz, Zy in Großbritannien oder Australien) – Auch bekannt als statischer Querschnittsmodul, und wird bei Biegespannungsberechnungen verwendet. Sie werden normalerweise für den oberen und unteren Faserquerschnitt berechnet. Zum Beispiel, ist Szt das Widerstandsmoment um die Z-Achse für die obere Faser des Querschnitts.
- Torsionskonstante (J.) - Auch bekannt als polares Trägheitsmoment oder J, ist ein Wert, der den Widerstand eines Materials gegen Verdrehung oder Torsionsverformung beschreibt.
- Der plastische Querschnittsmodul (S.) - ein Maß für die Fähigkeit einer Querschnittsform, einer plastischen Biegung zu widerstehen, Er wird verwendet, um die Spannung eines Materials abzuschätzen, wenn es unter einer bestimmten Belastung beginnt, nachzugeben (seine plastische Grenze zu erreichen) und wird typischerweise für die Konstruktion und Analyse von Trägern unter Belastung verwendet.
Andere Parameter - Dies sind erweiterte Ergebnisse, die mit dem vollständigen SkyCiv Section Builder berechnet wurden:
- Produkt der Trägheit (um die Z- und Y-Achse): Ein Maß für den Widerstand einer Form gegen eine Drehung um eine bestimmte Achse, das dem Kreuzprodukt aus dem Abstand von der Achse zu einem beliebigen Punkt der Form und der entsprechenden Komponente des Trägheitsmoments des Punktes entspricht.
- Plastischer Querschnittsmodul (um die Z- und Y-Achse): Ein Maß für die Fähigkeit einer Querschnittsform, einer plastischen Biegung zu widerstehen, Er wird verwendet, um die Spannung eines Materials abzuschätzen, wenn es unter einer bestimmten Belastung beginnt, nachzugeben (seine plastische Grenze zu erreichen) ..
- Plastische neutrale Achse (um die Z- und Y-Achse): Eine Achse in einer Querschnittsform, durch die alle auf die Form wirkenden Kräfte verlaufen müssen, um eine plastische Verformung zu bewirken.
- Scherfläche (um die Z- und Y-Achse): Die Fläche einer Querschnittsform, die effektiv Scherkräften widersteht.
- Abstand des Scherzentrums zum Schwerpunkt (in der Z- und Y-Achse): Mit dem SkyCiv-Schwerpunktsrechner können Sie den Abstand zwischen dem Scherzentrum und dem Schwerpunkt einer Querschnittsform berechnen.
- Torsionskonstante (mit FEA): Ein Wert, der den Widerstand eines Materials gegen Verdrehung oder Torsionsverformung beschreibt, und mit Hilfe der Finite-Elemente-Analyse berechnet wird.
- Torsionsradius: Der Abstand von einer Achse, auf den sich die Fläche einer Querschnittsform konzentrieren muss, um die gleiche Torsionskonstante wie die tatsächliche Form zu erhalten.
- Verformungskonstante: Ein Wert, der die Widerstandsfähigkeit eines Materials gegen Verformung oder Verzerrung beschreibt.
- Monosymmetriekonstante (um die Z- und Y-Achse): Ein Maß dafür, wie symmetrisch eine Querschnittsform um eine bestimmte Achse ist, wobei ein Wert von Null eine perfekte Symmetrie anzeigt.
- Trägheitsradius (um die Z- und Y-Achse): Der Abstand von einer Achse, in dem die Fläche einer Querschnittsform konzentriert sein muss, um dasselbe Trägheitsmoment wie die eigentliche Form zu ergeben.
- Drehungswinkel der Hauptachse: Der Winkel zwischen der neutralen Achse und der Hauptachse einer Querschnittsform.
Über Trägheitsmoment, Schwerpunkte und andere Schnitteigenschaften
Darüber hinaus haben wir weitere Informationen zur Berechnung des Trägheitsmoments von Profilen zusammengestellt. Dieser umfassende Leitfaden soll dazu beitragen, eine umfassende Wissensbasis für alle Fragen im Zusammenhang mit Trägheitsmoment, Zentroide, Widerstandsmodul und andere wichtige geometrische Eigenschaften des Querschnitts. In den unteren Segmenten, enthalten wir das Trägheitsmoment, wie man den Schwerpunkt berechnet, Trägheitsmoment und allgemeine MOI-Gleichungen mit dem SkyCiv Trägheitsmoment und Schwerpunkt-Rechner.
Was ist Trägheitsmoment?
Das Trägheitsmoment (technisch als Flächenträgheitsmoment, oder zweites Flächenträgheitsmoment bekannt) ist eine wichtige geometrische Eigenschaft, die im Bauwesen verwendet wird. Es steht in direktem Zusammenhang mit der Dicke des Querschnitts.
Im Allgemeinen gilt, Je höher das Flächenträgheitsmoment, desto stärker ist der Querschnitt, und desto weniger wird er sich unter Belastung durchbiegen. Das Trägheitsmoment eines Rechtecks, oder irgendeine Form für diese Angelegenheit, oder einer anderen Form ist technisch gesehen ein Maß für das Drehmoment - das erforderlich ist, um die Masse um eine Achse zu beschleunigen.
Bestimmung des Trägheitsmoments - Rechteckig
Um das Trägheitsmoment eines Rechtecks zu berechnen, kann die Formel:
Ich = (b * h^3) / 12
I ist das Trägheitsmoment des Rechtecks
b ist die Breite des Rechtecks
h ist die Höhe des Rechtecks
Es ist wichtig, dass die Maßeinheiten für b und h konsistent sind (z.B., Zoll, Millimeter, etc.). Die Einheit des Endergebnisses hängt auch von der Eingabeeinheit ab, z.B. wenn die Eingabe in Meter erfolgt, ist die Einheit des Ergebnisses m^4.
Beispielberechnung des Trägheitsmoments
Nehmen wir an, wir haben ein Rechteck mit den folgenden Abmessungen:
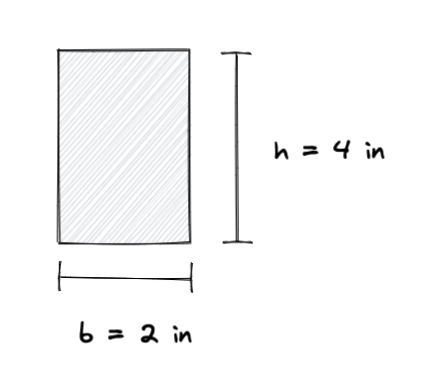
Verwenden Sie die Formel für das Trägheitsmoment, Wir können das Trägheitsmoment des Rechtecks wie folgt berechnen:
Ich = (b * h^3) / 12
Ich = (2 * 4^ 3) / 12
Ich = (2 * 64) / 12
= 10.67 in^4 anzeigt
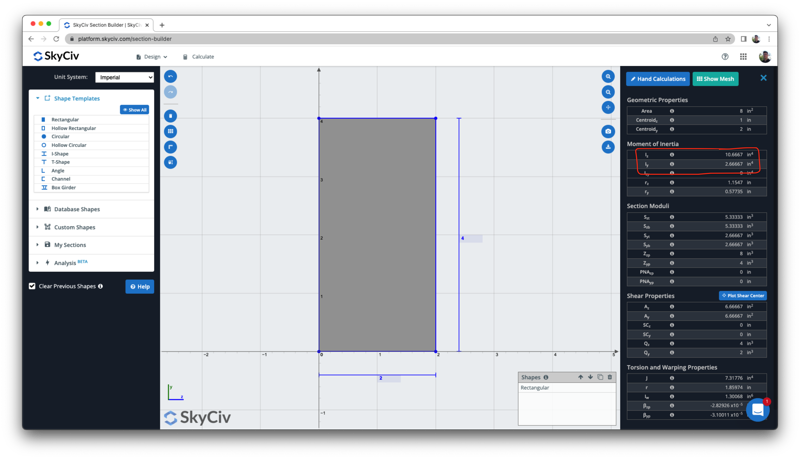
Also ist das Trägheitsmoment des Rechtecks 10.67 Zoll^4. Trägheitsmoment befindet sich um die Schwerachse, denken Sie daran, wenn Sie das Trägheitsmoment um eine andere Achse finden müssen, müssen Sie eine andere Formel verwenden oder eine Transformation durchführen. Sie können auch überprüfen, ob die Einheit immer das Produkt der Leistung der Eingabeeinheit ist, in diesem Fall sind alle Eingabeeinheiten Zoll, also ist das Ergebnis in Zoll^4.
Wir können dieses Ergebnis mit dem obigen freien Trägheitsmomentrechner überprüfen, der das gleiche Ergebnis von 10.6667 in^4 anzeigt:
Bestimmung des Trägheitsmoments - Ich glänze
Betrachten wir nun einen komplexeren Fall, bei dem der Querschnitt ein I-Träger, mit unterschiedlichen Flanschabmessungen ist. Das Konzept ist das gleiche, aber der Ansatz ist in diesem Fall ganz anders. Grundsätzlich, Im Prinzip müssen wir den I-Träger als eine Kombination verschiedener Rechtecke betrachten und die verschiedenen Teile addieren, um das gesamte Trägheitsmoment der Querschnitte zu erhalten. Kurz gesagt, Zusammenfassend müssen wir diese drei Schritte befolgen:
- Berechnung der neutralen Achse für den gesamten Querschnitt
- Berechnen Sie das Trägheitsmoment für jeden einzelnen Teil
- Berechnen des Trägheitsmoments mit Hilfe des Parallelachsensatzes - dies ist im Wesentlichen die Summe der einzelnen Trägheitsmomente
Betrachten wir also den folgenden Abschnitt:
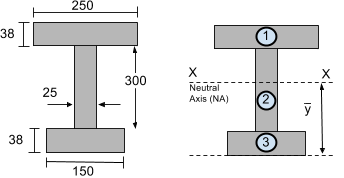
Die neutrale Achse (N / A) befindet sich im Schwerpunkt. Sie ist im Wesentlichen ein gewichteter Mittelwert der Fläche und des Abstands vom Boden für jedes Segment. Wir brauchen nur die Zentroidgleichung zu verwenden, um die Vertikale (j) den Schwerpunkt einer Form mit mehreren Segmenten zu berechnen.

Die Bezugslinie befindet sich an der Unterseite des Trägerquerschnitts. Für jedes Segment des oben gezeigten I-Trägerquerschnitts sind Ai und yi zu bestimmen, um den vertikalen Schwerpunkt bzw. den Schwerpunkt y zu ermitteln.


Jetzt haben wir den Schwerpunkt. Wir können nun das Trägheitsmoment berechnen. Um das Gesamtträgheitsmoment des Querschnitts zu berechnen, müssen wir das "Parallelachsentheorem" wie unten definiert verwenden:

Da wir es in drei rechteckige Abschnitte unterteilt haben, müssen wir das Trägheitsmoment für jeden dieser Abschnitte berechnen. Wir können jetzt die vereinfachte rechteckige Trägheitsmomentformel verwenden:
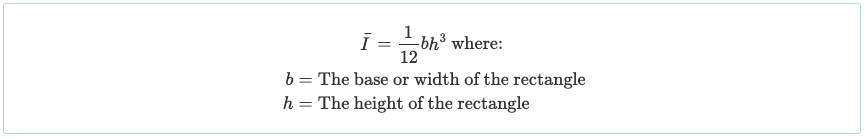
Jetzt haben wir alle Informationen, die wir brauchen, um mit dem "Parallelachsentheorem" das Gesamtträgheitsmoment des I-Trägerquerschnitts zu bestimmen. In unserem Beispiel:

Noch einmal, Wieder können wir dieses Ergebnis mit dem des freien Trägheitsmomentrechners vergleichen, um die Ergebnisse des Schwerpunkts und des Trägheitsmoments zu vergleichen, wo sowohl der Schwerpunkt (216.29 im) als auch das Trägheitsmoment (4.74 x 10^8 Zoll^4) Spiel haben:
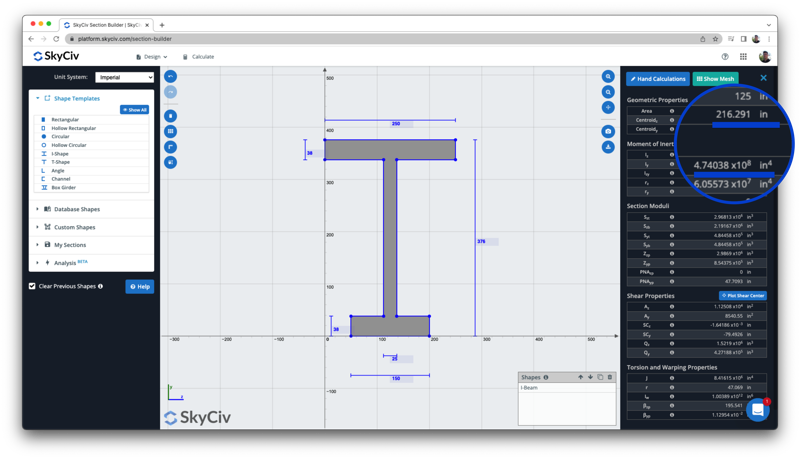
Für mehr Informationen, Besuchen Sie unser Tutorial auf Berechnung des Trägheitsmoments eines Balkenabschnitts.
Gleichungen für Trägheitsmomente
Für die Berechnung des Trägheitsmoments üblicher Formen und Querschnitte können auch einfache Gleichungen verwendet werden. Es handelt sich um schnelle Trägheitsmomentberechnungen, die schnelle Werte liefern und eine gute Möglichkeit darstellen, Querverweise zu erstellen oder Ihre Ergebnisse zu überprüfen. Konzentrieren Sie sich nur auf einfache Formen, Das folgende Diagramm zeigt einige dieser Gleichungen:
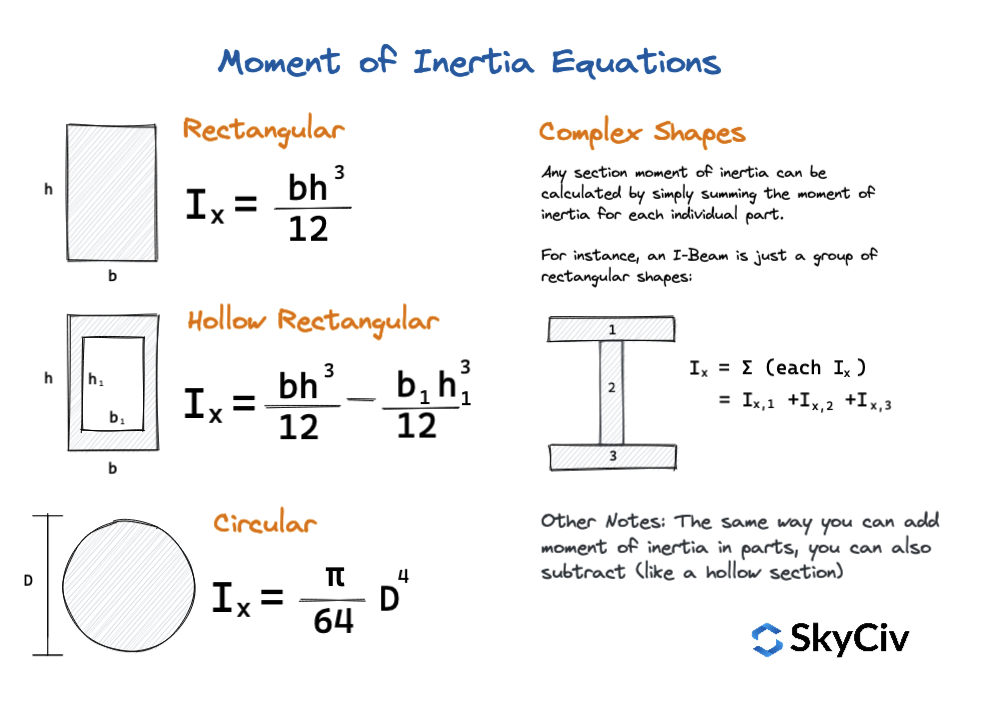
SkyCiv Schwerpunkt-Rechner
Ein Schwerpunkt, auch „geometrischer Mittelpunkt“ genannt, ist der Massenmittelpunkt eines Objekts mit einheitlicher Dichte. Eine vereinfachte Veranschaulichung eines Schwerpunktes wäre die Stelle, an der man einen Bleistift ansetzen müsste, um ihn auf dem Finger balancieren zu lassen. Die Stelle, an der der Bleistift im Gleichgewicht ist und nicht vom Finger fällt, wäre die ungefähre Stelle des Schwerpunkts des Bleistifts. Die Masse und Dichte des Materials werden berücksichtigt, um den Punkt zu bestimmen, an dem die Masse des Bleistifts auf beiden Seiten des Fingers gleich ist, und somit den "Schwerpunkt" des Bleistifts darstellt.
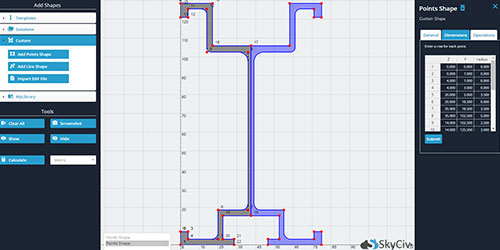
Der SkyCiv Centroid Calculator verwendet FEA, um innerhalb von Sekunden hochpräzise Ergebnisse zu liefern, egal wie komplex die Form ist. In der Premium-Version, kann der Benutzer die Koordinaten der Punkte eingeben, die die Form definieren, und unser Rechner liefert die Koordinaten des Schwerpunkts. Dies beinhaltet die Möglichkeit, benutzerdefinierte Formen durch DXF-Import, mehrere (konstruierte) Formen und benutzerdefinierte Punktformen zu entwerfen.
Unser Schwerpunktrechner ist nicht nur schnell und genau, sondern auch unglaublich einfach zu bedienen. Über eine einfache Benutzeroberfläche, können Sie Ihre Querschnittsabmessungen eingeben und erhalten die Querschnittswerte (einschließlich des Querschnittsschwerpunkts) in Sekundenschnelle. Ob Sie an einem Entwurfsprojekt arbeiten, mit verschiedenen Querschnitten experimentieren oder für eine Prüfung lernen, der SkyCiv Schwerpunktrechner ist das perfekte Werkzeug, um Sie bei Ihrer Arbeit zu unterstützen.
Abschnittsmodulrechner
Wie bereits erwähnt, können Sie mit diesem kostenlosen Tool auch den Elastizitätsmodul berechnen, aber wenn Sie ein Ingenieur sind, verstehen Sie vielleicht nicht, was der Widerstandsmoment ist. Einfach ausgedrückt, ist der Elastizitätsmodul eine Querschnittseigenschaft, die den Biegewiderstand eines Querschnitts misst und als Verhältnis des Trägheitsmoments zum Abstand zwischen der neutralen Achse und der am weitesten entfernten Faser berechnet wird. Der Elastizitätsmodul ist in dieser Gleichung einfach dargestellt:
Wo,
- S ist der Abschnittsmodul
- I ist das Trägheitsmoment des Abschnitts um die neutrale Achse
- y ist der Abstand von der neutralen Achse zum am weitesten entfernten Punkt des Abschnitts
Es gibt zwei Arten von Querschnittsmodulen: elastisch und plastisch. In Amerika, wird S typischerweise verwendet, um sich auf den elastischen Querschnittsmodul zu beziehen, während Z verwendet wird, um sich auf den plastischen Querschnittsmodul zu beziehen. Im Vereinigten Königreich und in Australien, ist es umgekehrt. Der elastische Modul wird normalerweise mit dem Buchstaben Z bezeichnet, während der plastische Modul mit dem Buchstaben S bezeichnet wird.
Im Allgemeinen, wird der Elastizitätsmodul für die Bemessung von Querschnitten verwendet, da er für die meisten Metalle bis zur Streckgrenze anwendbar ist. Metalle werden normalerweise nicht über die Streckgrenze hinaus ausgelegt.
Zusätzliche Dokumentation
Weitere Informationen über das Trägheitsmoment, seine Berechnung für verschiedene Formen, Formen und die Verwendung unseres Schwerpunktrechners finden Sie auf den folgenden Seiten:
Weitere kostenlose Tools verfügbar
SkyCiv bietet auch andere Tools an, z. B. das I-Beam-Size-Tool und eine kostenlose Konstruktionssoftware. Die Schublade für dynamische Abschnitte zeigt Ihnen auch eine grafische Darstellung Ihres Balkenabschnitts. Wenn Sie also das Trägheitsmoment des Kreises berechnen möchten, Trägheitsmoment eines Rechtecks oder einer anderen Form, Sie können gerne die unten stehende Software oder unseren All-Inclusive-SkyCiv Section Builder verwenden.
SkyCiv bietet eine breite Palette an Cloud-Strukturanalyse- und Entwurfssoftware für Ingenieure. Als ein sich ständig weiterentwickelndes Technologieunternehmen sind wir bestrebt, bestehende Arbeitsabläufe zu erneuern und zu hinterfragen, um Ingenieuren bei ihren Arbeitsprozessen und Entwürfen Zeit zu sparen.
Benötigen Sie mehr Funktionalität?
Upgrade auf a professioneller Plan um alle Funktionen freizuschalten