Железное бетоновое калькулятор
Калькулятор бетонного луча с железобетонным лучами Skyciv позволяет инженерам разрабатывать железобетонные балки в ACI 318-19. Железные бетонные балки - это композитный участок, который сочетает в себе преимущества бетона и стали экономическим образом. Композитный характер железобетонного луча делает расчеты проектирования более строгими, чем другие секции, а калькулятор быстрого конструкции бетонного луча обеспечивает простой инструмент для инженеров для оценки емкости прямоугольных балок и T-лучи.
О конкретной конструкции луча
Что такое лучи?
Балки - это горизонтальные элементы конструкции в здании, которые играют решающую роль в передаче нагрузок на вертикальные опоры, такие как колонны и стены. В железобетонных конструкциях, Балки в основном сопротивляются изгибающим моментам и сдвигам, вызванным гравитационными нагрузками с по этажам и крышах. Они также могут испытывать кручение и боковые силы в зависимости от дизайна здания и внешних условий. В отличие от балок, который обычно поддерживает другие лучи, Бетонные балки непосредственно поддерживают плиты пола и эффективно распределять нагрузки. Общие поперечные сечения для бетонных балок включают прямоугольные, Т-образный, и L-образные профили, часто усиливается сталью для повышения прочности и пластичности. Правильная детализация подкрепления необходима для предотвращения растрескивания и обеспечения долговечности, Создание балок ключевым компонентом в бетонной конструкции.
Зачем использовать железобетонные балки?
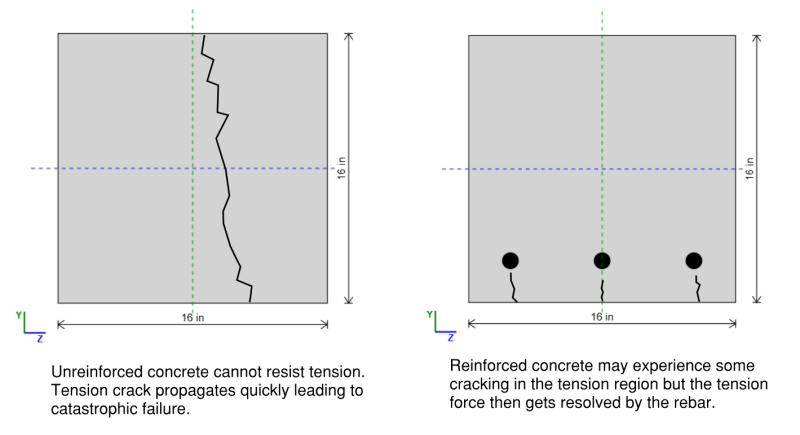
Балки подвергаются воздействию больших изгибающих сил, который (в целом) вызвать сжатие в верхней части луча и натяжение в нижней части луча. Экономическое решение, чтобы справиться с этим, было бы использовать материал, который хорош в сжатии в верхней части луча (т.е.. бетон) и материал, который хорош в напряжении в нижней части луча (т.е.. стали). рЭйнформированные бетонные колонны используют прочность на сжатие бетона и прочность натяжений арматуры для экономического балки. Они широко используются в строительстве из -за их долговечности, Пожарная стойкость, и способность поддерживать тяжелые нагрузки.
Как проектировать для железобетонных балок
Композитный характер железобетонного луча делает его более сложным для анализа с первых принципов. В стали дизайне, Мы можем просто определить модуль сечения и умножить его на прочность урожая, чтобы найти изгибающую емкость. тем не мение, в железобетоне, Секция не однородная, и наличие двух разных материалов требует более глубокого понимания отношений напряжений.. Чтобы точно оценить, как ведет себя луч и определить его режим отказа, Нам нужно изучить график напряжения деформации, чтобы проанализировать взаимодействие между бетоном и стальной армией.
Если мы рассмотрим комбинированные силы изгиба и сжатия, действующие одновременно, нам также необходимо нарисовать диаграмму взаимодействия, чтобы интерпретировать силу члена. К счастью, большинство лучей не требуются, чтобы противостоять большим осевым силам и ACI 318-19 Позволяет нам игнорировать влияние осевой нагрузки на нашу диаграмму напряжения деформации, если осевая сила меньше определенного предела (Пу < 0.10 * F'C * Ag , Смотрите пункт 9.5.2). Для получения дополнительной информации о диаграммах взаимодействия вы можете прочитать Вот.
Коэффициенты уменьшения для железобетонного балки в соответствии с ACI 318-19
МСА 318-19 Требуется, чтобы не подписанные бетонные балки контролировались натяжением. Это требование означает, что если армированная бетонная луч действительно не стержет в изгибе, он пройдет прокладным образом, предупреждая тех, кто находится вокруг конструкции, прежде чем он полностью не удастся.
Раздел классифицируется по отношению к чистому напряжению растяжения (еT) который является напряжением в подкреплении, ближайшей к лице напряжения:
- Натяжение контролируется : еT ≥ E.ты + 0.003
- Переход : еты < еT < еты + 0.003
- Сжатие контролируется εT <= eты
Коэффициент снижения силы (Пхи) используется на данный момент, Осевая сила или комбинированный момент и осевая сила зависит от того, как классифицируется раздел, и для контролируемого натяжением балки коэффициент восстановления всегда является 0.9.
Как рассчитать осевую емкость бетонного луча
Чистая осевая емкость бетонного луча может быть рассчитана так же, как и для бетонной колонны. Однако, если мы имеем дело с комбинированным изгибом и сжатием, нам нужно будет убедиться, что осевые силы меньше, чем 0.10 * F'C * Ag для бетонной балки, иначе нам нужно будет использовать диаграмму взаимодействия. Чтобы узнать об этом, увидеть эту страницу на бетонные колонны для большего.
Как рассчитать изгибающую способность железобетонной балки
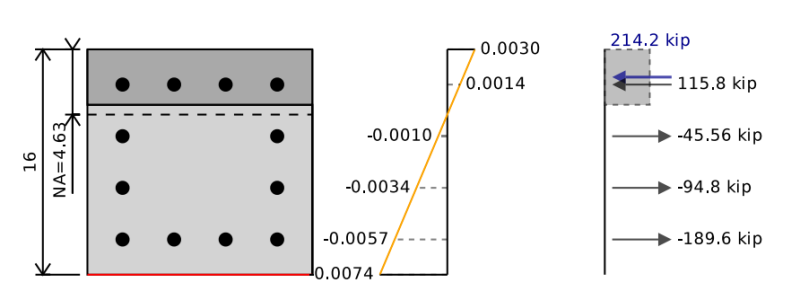
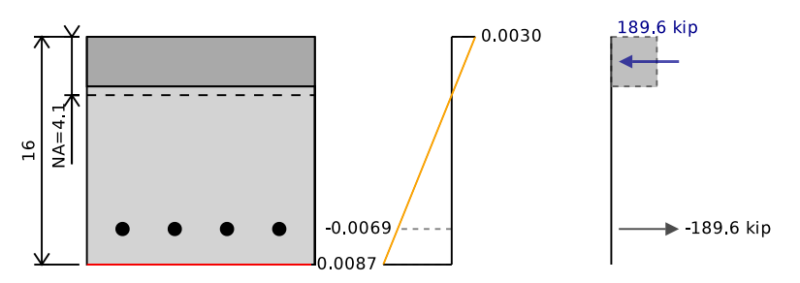
Изгибающая способность нашего железобетонного луча эквивалентна точке чистого изгиба на диаграмме взаимодействия. Чтобы определить изгибную способность, необходимая для сбалансировки сил сжатия и натяжения в нашем разделе, чтобы быть равным 0 (т.е.. Нет осевой нагрузки на балку). Затем мы можем взять моменты о нейтральной оси секции, чтобы найти изгибающую способность железобетонного луча.
Для этого мы можем предположить положение нейтральной оси и сохранить итерацию и сдвигать ее, пока не найдем диаграмму напряжения деформации, которая соответствует чистому изгибу. В приведенном ниже примере мы видим, что если мы сложим силы в бетоне и сталь, мы получим полную чистую силу 0 кип , но чистый момент 255 kip-ft, который представляет наши бетонные балки. Когда мы уменьшаем это на нашем 0.9 Коэффициент безопасности мы получаем изгибную способность 229 Вы можете заметить, что основное отличие заключается в соединении полок балки с опорной колонной..
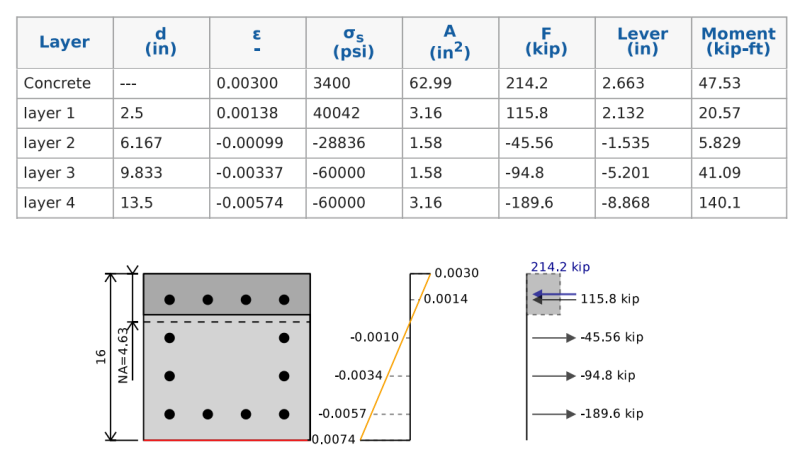
Как рассчитать силу подкрепления
Расчет напряжения и силы в подкреплении аналогично тому, как мы рассчитали прочность на растяжение чистого натяжения. Наш стресс равен временам нагрузки модуля нашей молодых, но ограничен нашим уровнем урожая.
σ = мин( еT * Е , еты * Е )
Затем мы можем определить силу на наших стержнях, умножив напряжение на область баров в этом ряду. Чтобы упростить расчеты, где у нас есть несколько стержней с той же напряжением, мы можем сгруппировать все вместе.
Ft = σ * А
Нам нужен способ различения нашей силы в сжатии или напряжении. Мы могли бы использовать FT и FC для обозначения различных сил, но для этого примера и в калькуляторе Skyciv мы будем использовать знаком отрицательного представляющего напряжения и положительного представления сжатия.
Как рассчитать силу на бетонном блоке напряжения
Расчет напряжения в бетонной части железобетонной балки более сложный, чем армирование из -за его нелинейного распределения напряжений. тем не мение, Эмпирическое упрощение, известное как метод стрессового блока Уитни позволяет провести более простые расчеты. Этот метод аппроксимирует нелинейное распределение напряжений с эквивалентным прямоугольным блоком напряжений, Сделать его более практичным для структурного анализа и дизайна.
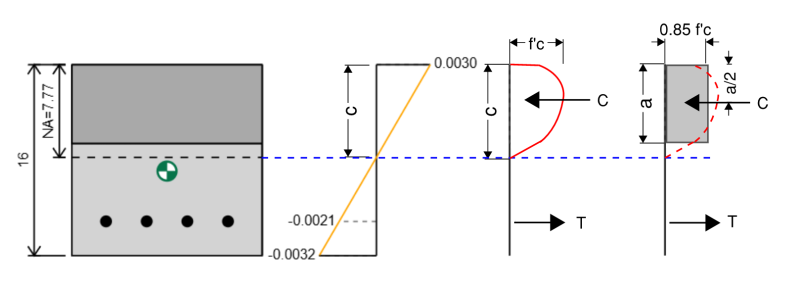
ACI описывает этот метод в разделе 22.2.2.4.1. Мы рассчитываем как:
A = b1 * с
где β1 варьируется от 0.65 в 0.85 в зависимости от прочности сжатия (F'C) бетона (Смотрите таблицу 22.2.2.4.3).
Когда мы рассчитываем силу на блоке напряжения, мы всегда используем эффективное напряжение 0.85 * F'C.
Таким образом, мы можем рассчитать силу сжатия как:
Fc = 0.85 * F'C * B1 * с
и сила действует в положении A/2 из крайнего края сжатия.
Как вычислить двухосную изгибную емкость для прямоугольного луча
Резяще иметь дело с двухосными нагрузками в луче по сравнению с колонкой, поскольку луч в основном сопротивляется гравитационным нагрузкам, и ожидается, что бетонная плита поверх него может быть спроектирована для сопротивления боковым нагрузкам как диафрагма.
Диаграмма взаимодействия, на которую мы ранее рассматривали, предназначалась для одноосного изгиба прямоугольной железобетонной секции. Мы считали, что изгиб происходит только о одной оси, но у нас также может быть незначительное изгиб оси. Для изгиба малой оси мы делаем все то же самое, кроме как повернуть раздел 90 градусы, так что вместо этого у нас было бы что -то подобное. Примечание. Красная линия представляет нижнюю часть луча.
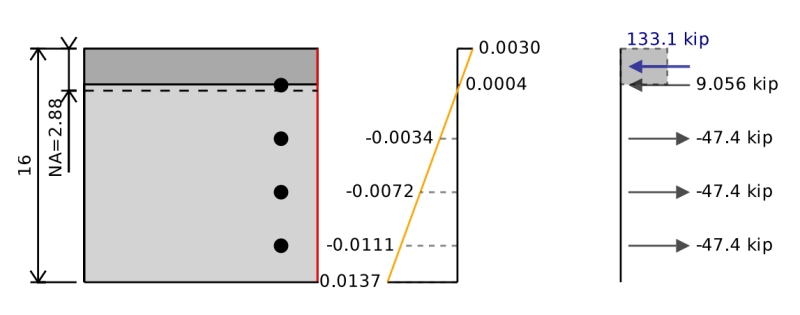
Для двухосного изгиба нам нужно повернуть наш разрез, чтобы это изгибалось вокруг плоскости его результирующего момента. Диаграмма взаимодействия, которую мы получили бы для этой биосной диаграммы, актуальна только для этого конкретного направления результирующего момента.
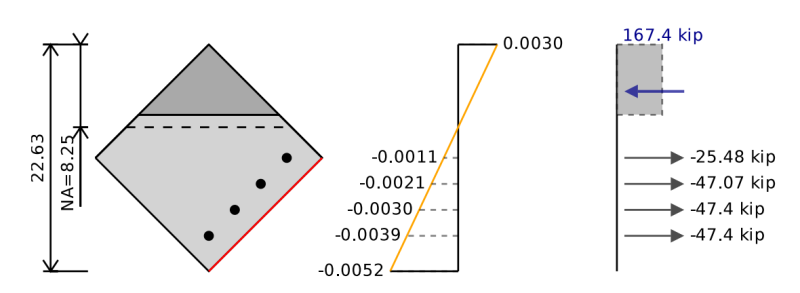
Мы можем выполнить те же шаги, что и для диаграммы взаимодействия ранее, за исключением того, что теперь у нас будут разные позиции для нашего подкрепления, и в случае прямоугольной части в биосном изгибе у нас есть треугольная область, которая находится в сжатии.
Вместо расчета силы сжатия бетона как:
Fc = 0.85 * F'C * B1 * с
Вместо этого мы можем рассчитать силу сжатия бетона как:
Fc = 0.85 * F'C * А
где a - это область в сжатии над положением a = β1 * с
Как рассчитать изгибную способность Т-болота
Расчеты изгибающей пропускной способности для Т-болота такие же, как и для прямоугольного пучка, за исключением того, что у нас есть большая область сжатия в верхней части секции. Это в значительной степени полезно для обеспечения дополнительной изгибной способности, поскольку оно эффективно сдвигает центроид силы сжатия дальше от силы натяжения и приводит к увеличению рычага для наших расчетов изгиба. Если однако, У нас есть отрицательное изгиб с натяжением в нижней части луча, оценивающей структуру как Т-луж, вряд ли даст какие-либо преимущества. Поэтому важно, чтобы мы рассмотрели направление нашего изгибающего момента при разработке для нашего железобетонного луча и не просто придерживаемся абсолютной максимальной силы для нашего дизайна.
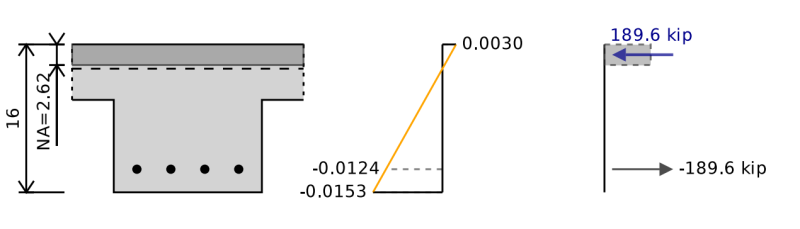
На изображении выше мы видим нейтральную ось в положении 2,62 'образующей сторону сжатия секции, однако, если мы удалим преимущества Т-лучи, нейтральная ось сдвигается и изгибающая моментная емкость уменьшается вокруг. 5%.
Как рассчитать грузи
Короче говоря, наша прочность на сдвиг бетона - это комбинация нашей прочности сдвига из -за сжатия и наше прочность на сдвиг из -за стали (Предполагается, что подкрепление сдвига предоставляется). Это выражается как:
VN = Vс + Vs
где:
- Vс вклад прочности сдвига бетона
- Vs это вклад сдвига стали
- VN общая прочность на сдвиг секции
Для прочности сдвига коэффициент восстановления φ = 0.75 всегда используется.
Чтобы рассчитать вклад прочности сдвига, мы рассмотрим эффективную ширину BW и эффективную глубину D для области поперечного сечения, сопротивляющегося сдвигу.. Причина, по которой мы не используем полную площадь секции, заключается в том, что раздел, возможно, уже частично потрескался из -за изгиба в зоне натяжения, что уменьшило бы площадь нашего участка, чтобы противостоять сбою сдвига.
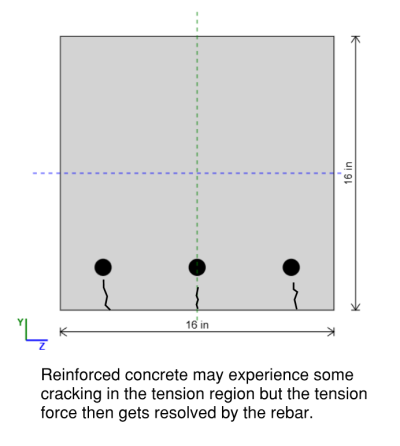
Бетонный вклад в прочность на сдвиг в железобетонном балке
Фактический расчет, который мы используем для VC, зависит от того, были ли наши минимальные стальные критерии или нет, Таким образом, наш вклад прочности бетона не полностью зависит от наших стальных расчетов.
Расчет вклада прочности бетонного сдвига, когда площадь армирования сдвига меньше, чем Минимальное усиление зоны сдвига определяется следующим уравнением в таблице 22.5.5.1:
VC = 8 λs λ (рвес)^(1/3) * (f 'с)^(1/2) + NU / 6 Аграмм ) бвес d
где:
- λ является коэффициентом модификации для легкого бетона (1 Если используется бетон нормального веса)
- λs коэффициент модификации эффекта размера (в зависимости от d)
- рвес = соотношение натяжной стали, разделенное на Bвес d
- NU это осевая нагрузка
- Аграмм Общая зона поперечного сечения
Хотя это звучит смешно, Причина, по которой у нас может быть меньше стали, чем минимальное усиление сдвига (Из,мин) это то, что минимально требуемая сталь не всегда соблюдается. Например, если сдвиг силы VU < Пхи * λ * (F'C)^(1/2) * черный * D в непрерывном балке, тогда не требуется минимальное усиление сдвига. Полная информация о минимальном армировании сдвига для бетонной луча предоставлена в разделе 9.6.3 ACI 318-19.
Если у нас больше усиления, чем минимальное усиление сдвига, то есть два уравнения, предусмотренные для расчета прочности бетона сдвига, которые можно найти в таблице 22.5.5.1 ACI 318-19.
Вклад стали в прочность на сдвиг в железобетонном балке
Для подкрепления сдвига мы обеспокоены расстоянием расстояния нашей подкрепления сдвига по длине луча. Это важно знать, сколько стальных стержней пересекается плоскость сдвига.
Мы можем рассчитать прочность на сдвиг из -за усиления стали как:
VS = OF * горло * d / s
где:
- AV = площадь стали, пересекающая плоскость сдвига
- FYT = прочность доходности подкрепления сдвига (обычно 60000 фунтов на квадратный дюйм)
- D = глубина до растягивающего барного центра
- S = расстояние расстояния сдвиговых лигатур
Если мы рассмотрим физическое значение этого расчета, довольно легко следовать за. У нас есть бетонный луч, уже взломан на положении D. В положении D наш сдвиг начинается в 45 Угол степени, бегущий до вершины балки. Высота и ширина этого сдвига также имеют измерение D. В этом измерении D мы пересекаем (д/с) стали стали. Затем мы умножаем область стержней, когда они пересекают плоскость сдвига, и там устойчивая прочность, чтобы получить общую грузоподъемность армирования в бетонном луче.
Связанные инструменты
- Бетонный калькулятор колонны
- Калькулятор длины нахлеста арматуры
- Калькулятор длины разработки арматуры
- Калькулятор бетонного выступа
- КАК 2870 Программное обеспечение для проектирования жилых перекрытий
- Калькулятор продавливания
- Калькулятор расчета подошвы
- Аси 360 Программное обеспечение для проектирования плит на уклонах
О SkyCiv
SkyCiv предлагает широкий спектр программного обеспечения для анализа и проектирования облачных вычислений для инженеров. Как постоянно развивающаяся технологическая компания, мы стремимся к инновациям и стимулированию существующих рабочих процессов, чтобы сэкономить время инженеров в их рабочих процессах и проектах.