Stahlbetonbalkenrechner
Mit dem Skyciv -Stahlbeton -Balkenrechner können Ingenieure Stahlbetonstrahlen zum ACI gestalten 318-19. Stahlbetonstrahlen sind ein Verbundabschnitt, der die Vorteile von Beton und Stahl auf wirtschaftliche Weise kombiniert. Die zusammengesetzte Natur eines Stahlbetonstrahls macht Auslegungsberechnungen strenger als andere Abschnitte, und der Quick Design Betonstrahlrechner bietet Ingenieuren ein einfach.
Über Betonbalkendesign
Was sind Balken??
Balken sind horizontale Strukturmitglieder in einem Gebäude, das eine entscheidende Rolle bei der Übertragung von Lasten auf vertikale Stützen wie Säulen und Wände spielen. In Stahlbetonstrukturen, Balken widerstehen hauptsächlich Biege Momenten und Scherkräften, die durch Schwerkraftbelastungen von Böden und Dächern verursacht werden. Sie können auch Torsions- und Seitenkräfte in Abhängigkeit vom Design und der externen Bedingungen des Gebäudes erleben. Im Gegensatz zu Trägern, die typischerweise andere Strahlen unterstützen, Betonbalken stützen die Bodenplatten direkt und verteilen Sie Lasten effizient. Gemeinsame Querschnitte für Betonbalken sind rechteckig, T-förmig, und L-förmige Profile, oft mit Stahl verstärkt, um die Festigkeit und Duktilität zu verbessern. Die ordnungsgemäßen Verstärkungsdetails sind wichtig, um ein Knacken zu verhindern und die Haltbarkeit zu gewährleisten, Strahlen zu einer Schlüsselkomponente in der Betonkonstruktion machen.
Warum verstärkte Betonbalken verwenden??
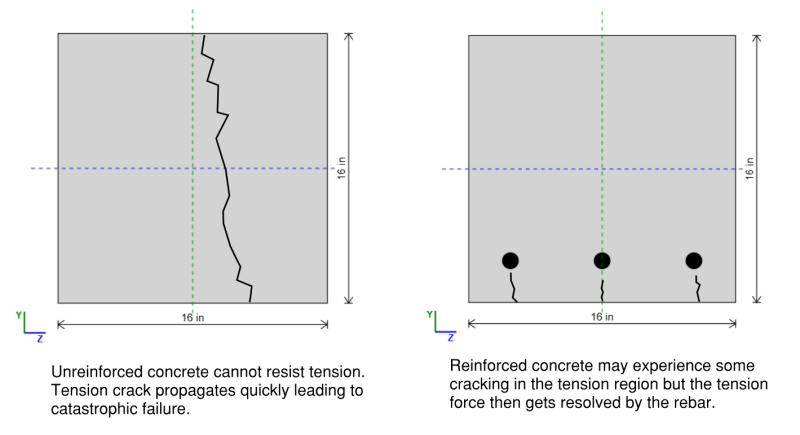
Balken sind großen Biegerkräften ausgesetzt, welcher (allgemein) induzieren Kompression oben am Strahl und die Spannung am Boden des Strahls. Eine wirtschaftliche Lösung, die damit umgeht (d.h.. Beton) und ein Material, das am Boden des Strahls gut in der Spannung ist (d.h.. Stahl). R.Einheitliche Betonsäulen verwenden die Kompressionsstärke von Beton und Spannungsstärke von Bewehrungsstärke für ein wirtschaftliches Strahlentwurf. Sie sind aufgrund ihrer Haltbarkeit häufig im Bauwesen eingesetzt, Feuerwiderstand, und Fähigkeit, schwere Lasten zu unterstützen.
So entwerfen Sie für Stahlbetonstrahlen
Die zusammengesetzte Natur eines Stahlbetonstrahls macht es komplexer, aus den ersten Prinzipien zu analysieren. In Stahldesign, Wir können einfach den Abschnittsmodul bestimmen und ihn mit der Ertragsfestigkeit multiplizieren, um die Biegerkapazität zu finden. Jedoch, in verstärktem Beton, Der Abschnitt ist nicht homogen, und das Vorhandensein von zwei verschiedenen Materialien erfordert ein tieferes Verständnis der Stress-Dehnungs-Beziehung. Um genau zu beurteilen, wie sich der Strahl verhält und seinen Fehlermodus feststellt, Wir müssen in das Spannungs-Dehnungs-Diagramm prüfen, um die Wechselwirkung zwischen Beton und Stahlverstärkung zu analysieren.
Wenn wir in Betracht ziehen, mischte Bieger- und Kompressionskräfte gleichzeitig wirken, müssten wir auch ein Interaktionsdiagramm zeichnen, um die Stärke des Mitglieds zu interpretieren. Zum Glück sind die meisten Strahlen nicht erforderlich, um großen axialen Kräften und dem ACI zu widerstehen 318-19 Lassen Sie uns die Auswirkungen der axialen Belastung auf unser Spannungs-Dehnungs-Diagramm ignorieren, wenn die axiale Kraft geringer ist als eine bestimmte Grenze (Pu < 0.10 * Die Scherfestigkeit entspricht einer kombinierten Schertragfähigkeit des Betons und der Stahlbewehrung * Ag , Siehe Klausel 9.5.2). Weitere Informationen zu Interaktionsdiagrammen können Sie lesen Hier.
Reduktionsfaktoren für Stahlbetonbalken -Design nach ACI 318-19
Der ACI 318-19 erfordert, dass nicht sprudelte Betonstrahlen spannungsgesteuert sind. Diese Anforderung bedeutet, dass ein Stahlbetonballe beim Biegen fehlschlägt..
Der Abschnitt wird in Bezug auf die Net -Zugstrecke klassifiziert (et) Welches ist die Belastung in der Verstärkung, die dem Spannungsgesicht am nächsten liegt:
- Mit Spannung kontrolliert : et ≥ ety + 0.003
- Übergang : ety < et < ety + 0.003
- Kompression kontrolliert εt <= ety
Der Festigkeitsreduktionsfaktor (Phi) für den Moment verwendet, Axiale Kraft oder kombinierte Moment und axiale Kraft hängen davon ab, wie der Abschnitt klassifiziert wird, und für einen spannungsgesteuerten Strahl ist der Reduktionsfaktor immer 0.9.
Wie man die axiale Kapazität eines Betonstrahls berechnet
Die reine axiale Kapazität eines Betonstrahls kann genauso berechnet werden wie für eine Betonspalte. Wenn wir jedoch mit kombiniertem Biegung und Komprimierung zu tun haben, müssen wir sicherstellen, dass die axialen Kräfte geringer sind als 0.10 * Die Scherfestigkeit entspricht einer kombinierten Schertragfähigkeit des Betons und der Stahlbewehrung * AG für einen Betonstrahl, sonst müssen wir ein Interaktionsdiagramm verwenden. Um dies zu erfahren, finden Sie diese Seite auf Betonspalten für mehr.
Wie berechnet man die Biegerkapazität eines Stahlbetonbalkens
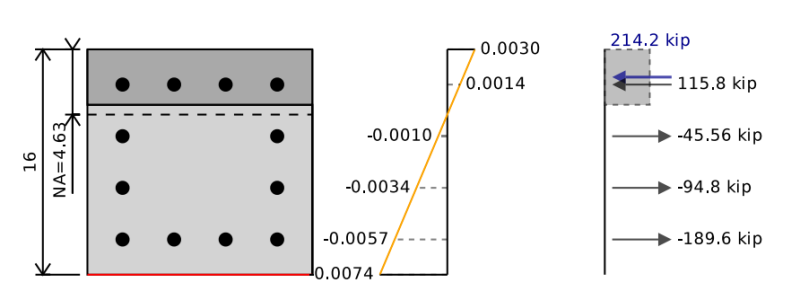
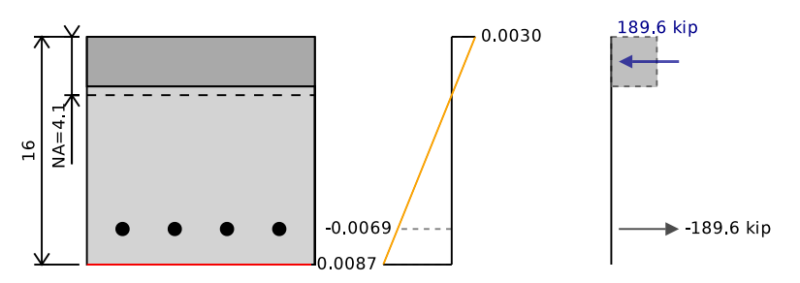
Die Biegekapazität unseres Stahlbetonbalkens entspricht dem Punkt der reinen Biegung eines Wechselwirkungsdiagramms. Um die Biegekapazität zu bestimmen, müssen wir die Kompressions- und Spannungskräfte in unserem Abschnitt ausgleichen, um gleich zu sein 0 (d.h.. Keine axiale Last, die auf den Strahl wirkt). Wir können dann Momente über die neutrale Achse des Abschnitts nehmen, um die Biegekapazität des Stahlbetonbalkens zu finden.
Dazu können wir eine Position einer neutralen Achse annehmen und sie weiterhin iterieren und verschieben, bis wir das Spannungs-Dehnungs-Diagramm finden. Im folgenden Beispiel können wir sehen, dass wir, wenn wir die Kräfte im Beton und im Stahl addieren, eine totale Nettokraft erhalten 0 kip, Aber ein Netto -Moment von 255 KIP-FT, der unsere Betonstrahlen ultimative Biegekapazität darstellt. Wenn wir dies durch unsere reduzieren 0.9 Sicherheitsfaktor Wir erhalten eine Design -Biegekapazität von 229 kip-ft.
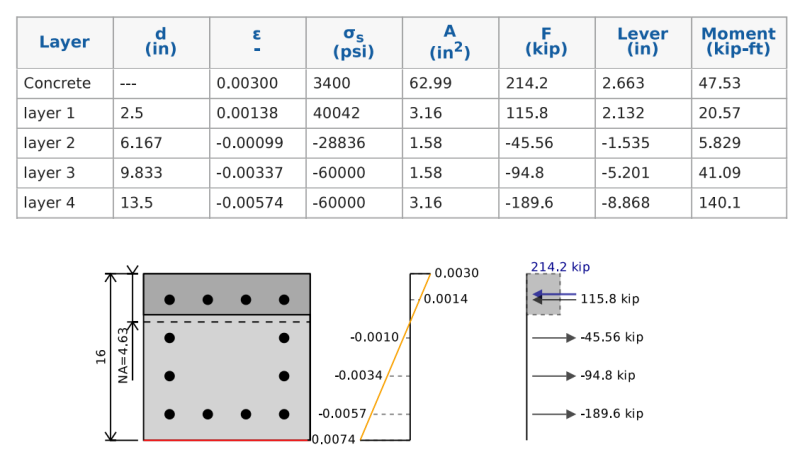
Wie man die Kraft auf die Verstärkung berechnet
Die Berechnung der Spannung und Kraft in der Verstärkung ähnelt der Art, wie wir die reine Spannungsstärke berechnet haben. Unser Stress entspricht unseren Belastungszeiten unseres Jungmoduls, aber durch unseren Ertragsstress begrenzt.
σ = min( et * E. , ety * E. )
Wir können dann die Kraft auf unseren Balken bestimmen, indem wir den Stress mit dem Bereich der Stangen in dieser Reihe multiplizieren. Um Berechnungen zu vereinfachen, bei denen wir mehrere Balken mit dem gleichen Belastung haben, können wir diese alle zusammen gruppieren.
Ft = σ * Ein
Wir brauchen eine Möglichkeit, zwischen unserer Kraft in Kompression oder Spannung zu unterscheiden. Wir könnten FT und FC verwenden, um die verschiedenen Kräfte zu bezeichnen, aber für dieses Beispiel und im Skyciv -Rechner werden wir eine Vorzeichenbeschreibung der negativen Spannung und der positiven Komprimierung verwenden.
Wie berechnet man die Kraft auf einem Betonspannungsblock
Die Berechnung der Spannung im Betonabschnitt eines Stahlbetonbalkens ist aufgrund seiner nichtlinearen Spannungsverteilung komplexer als die Verstärkung. Jedoch, Eine empirische Vereinfachung, die als Whitney Stress Block -Methode bekannt ist, ermöglicht einfachere Berechnungen. Diese Methode nähert sich der nichtlinearen Spannungsverteilung mit einem äquivalenten rechteckigen Spannungsblock, für die strukturelle Analyse und das Design praktischer machen.
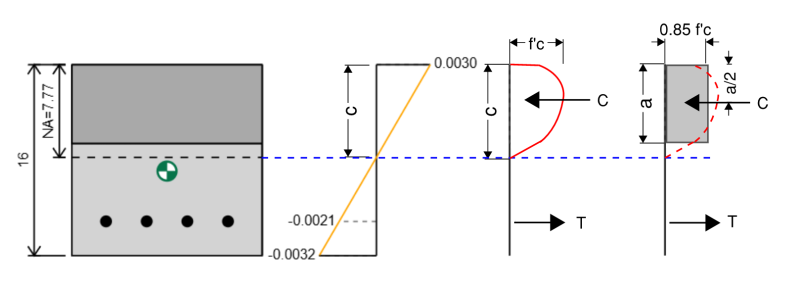
Das ACI beschreibt diese Methode im Abschnitt 22.2.2.4.1. Wir berechnen a as:
A = B1 * c
wo β1 reicht von 0.65 zu 0.85 Abhängig von der Kompressionsstärke (Die Scherfestigkeit entspricht einer kombinierten Schertragfähigkeit des Betons und der Stahlbewehrung) von Beton (Siehe Tabelle 22.2.2.4.3).
Wenn wir die Kraft auf dem Spannungsblock berechnen, verwenden wir immer einen wirksamen Stress von 0.85 * Die Scherfestigkeit entspricht einer kombinierten Schertragfähigkeit des Betons und der Stahlbewehrung.
So können wir die Kompressionskraft als berechnen:
Fc = 0.85 * Die Scherfestigkeit entspricht einer kombinierten Schertragfähigkeit des Betons und der Stahlbewehrung * B1 * c
und die Kraft wirkt an einer Position A/2 aus der extremen Komprimierungskante.
Wie berechnet man die biaxiale Biegekapazität für einen rechteckigen Strahl
Es ist seltener, sich mit biaxialen Belastungen in einem Strahl im Vergleich zu einer Säule zu befassen Membran.
Das Wechselwirkungsdiagramm, das wir uns zuvor angesehen haben. Wir haben die Biegung nur für eine Achse in Betracht gezogen, aber wir könnten auch eine kleinere Achsenbiegung haben. Für eine kleinere Achsenbiegung würden wir alles gleich tun, außer dass wir den Abschnitt drehen würden 90 Grad, also hätten wir stattdessen so etwas. Beachten Sie, dass die rote Linie den Boden des Strahls darstellt.
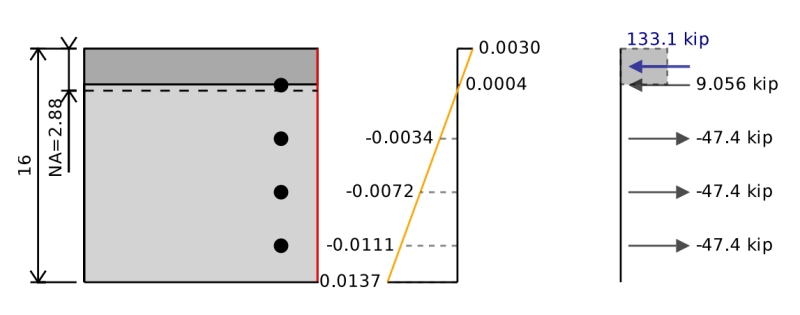
Für die biaxiale Biegung müssen wir unseren Abschnitt drehen. Das Interaktionsdiagramm, das wir für dieses biaxiale Diagramm erhalten würden, ist nur für diese besondere Richtung des resultierenden Moments relevant.
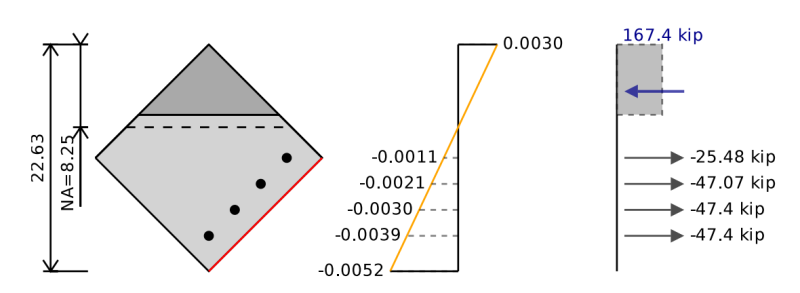
Wir können die gleichen Schritte wie für das Interaktionsdiagramm ausführen, außer jetzt werden wir unterschiedliche Positionen für unsere Verstärkung haben, und im Falle eines rechteckigen Abschnitts in biaxialer Biegung haben wir einen dreieckigen Bereich, der sich in Kompression befindet.
Anstatt die Betonkompressionskraft als zu berechnen:
Fc = 0.85 * Die Scherfestigkeit entspricht einer kombinierten Schertragfähigkeit des Betons und der Stahlbewehrung * B1 * c
Wir können stattdessen die Betonkompressionskraft als berechnen:
Fc = 0.85 * Die Scherfestigkeit entspricht einer kombinierten Schertragfähigkeit des Betons und der Stahlbewehrung * Ein
wobei a der Bereich in Kompression über der Position a = β1 ist * c
Wie berechnet man die Biegekapazität eines T-Strahls
Die Biegekapazitätsberechnungen für einen T-Strahl sind die gleichen wie bei einem rechteckigen Strahl, außer dass wir eine größere Kompressionsfläche oben im Abschnitt haben. Dies ist weitgehend von Vorteil, um eine zusätzliche Biegerkapazität bereitzustellen, da sie den Schwerpunkt der Kompressionskraft weiter von der Spannungskraft entfernt und zu einem erhöhten Hebelarm für unsere Biegeberechnungen führt. Wenn jedoch, Wir haben eine negative Biegung mit Spannungen am Boden des Strahls, in dem die Struktur bewertet wird, wenn ein T-Strahl keine Vorteile bietet. Es ist daher wichtig, dass wir die Richtung unseres Biegermoments bei der Gestaltung unseres Stahlbetonstrahls betrachten und nicht einfach die absolute maximale Kraft für unser Design einnehmen.
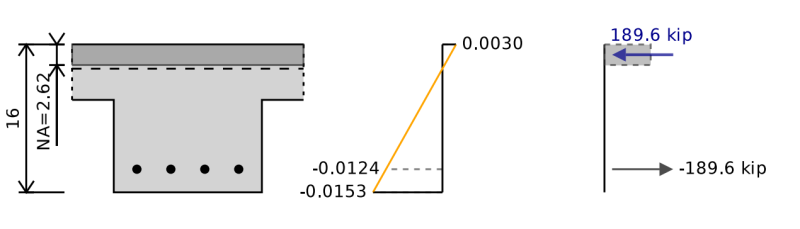
Im Bild oben sehen wir die neutrale Achse an einer Position von 2,62 'Form der Kompressionsseite des Abschnitts 5%.
Wie man die Scherkapazität eines Stahlbetonbalkens berechnet
Kurz gesagt, unsere Betonscherfestigkeit ist die Kombination unserer Scherfestigkeit aufgrund von Kompression und unserer Scherfestigkeit aufgrund von Stahl (Angenommen, die Scherverstärkung ist bereitgestellt). Dies wird ausgedrückt als:
V n = Vc + V s
wo:
- V c ist der Scherfestigkeitsbeitrag von Beton
- V s ist der Scherbeitrag von Stahl
- V n ist die Gesamtscherfestigkeit des Abschnitts
Für die Scherfestigkeit ist ein Reduktionsfaktor von φ = 0.75 wird immer verwendet.
Zur Berechnung des Beitrags der Scherfest. Der Grund, warum wir den vollständigen Abschnittsbereich nicht verwenden, ist, dass der Abschnitt möglicherweise bereits teilweise geknackt hat.
Betonbeitrag zur Scherfestigkeit in einem Stahlbetonbalken
Die tatsächliche Berechnung, die wir für VC verwenden, hängt davon ab, ob unsere Mindeststahlkriterien erfüllt wurden oder nicht, Unser Betonstärkebeitrag hängt also nicht ganz von unseren Stahlberechnungen ab.
Die Berechnung für den Beitrag der Betonscherfestigkeit, wenn der Bereich der Scherverstärkung ist weniger als Die minimale Verstärkung des Scherbereichs erfolgt durch die folgende Gleichung in der Tabelle 22.5.5.1:
Vc = 8 λs λ (rw)^(1/3) * (f'c)^(1/2) + N.u / 6 EinG ) bw d
wo:
- λ ist der Modifikationsfaktor für leichten Beton (1 Wenn Normalgewicht Beton verwendet wird)
- λs ist der Größeneffektveränderungsfaktor (abhängig von d)
- rw = Verhältnis von Spannstahl geteilt durch bw d
- N.u ist axiale Belastung
- EinG ist Brutto -Querschnittsbereich
Obwohl es lustig klingt, Der Grund, warum wir weniger Stahl haben als die minimale Scherverstärkung (Von,Min.) ist, dass der minimal erforderliche Stahl nicht immer durchgesetzt wird. Zum Beispiel, wenn die Scherkraft vu betreibt < Phi * λ * (Die Scherfestigkeit entspricht einer kombinierten Schertragfähigkeit des Betons und der Stahlbewehrung)^(1/2) * BW * D In einem nicht sprudelten Strahl ist die minimale Scherverstärkung nicht erforderlich, um bereitzustellen. Die vollständigen Details zur minimalen Scherverstärkung für einen Betonstrahl finden Sie in Abschnitt 9.6.3 von ACI 318-19.
Wenn wir mehr Verstärkung als die minimale Scherverstärkung haben, werden zwei Gleichungen zur Berechnung der Scherfestigkeit von Beton vorgesehen, die in der Tabelle gefunden werden können 22.5.5.1 des ACI 318-19.
Stahlbeitrag zur Scherfestigkeit in einem verstärkten Betonbalken
Für die Scherverstärkung befassen wir uns mit dem Abstand unserer Scherverstärkung entlang der Länge des Strahls. Dies ist wichtig zu wissen, wie viele Stahlstangen eine Scherebene schneiden würden.
Wir können die Scherfestigkeit aufgrund der Stahlverstärkung als berechnen:
Vs = von * Kehle * d / s
wo:
- AV = der Bereich des Stahls, der die Scherebene schnitt,
- FYT = die Ertragsfestigkeit der Scherverstärkung (normalerweise 60000 psi)
- d = die Tiefe zur Zugstange
- S = Abstand von Scherligaturen
Wenn wir die physische Bedeutung dieser Berechnung betrachten, ist es recht einfach, mitzumachen. Wir haben den Betonstrahl bereits auf Position D geknackt. In Position D beginnt unser Scherversagen bei a 45 Gradwinkel, der bis zur Oberseite des Strahls läuft. Die Höhe und Breite dieses Scherversagens ist ebenfalls von Dimension D.. Über diese Dimension d kreuzen wir uns (d/s) Stahlstangen. Wir multiplizieren dann den Bereich der Stäbe, wenn sie die Scherebene schneiden und dort die Festigkeit ergeben, um die Gesamtschubkapazität der Verstärkung im Betonstrahl zu erhalten.
Verwandte Tools
Über SkyCiv
SkyCiv bietet eine breite Palette an Cloud-Strukturanalyse- und Entwurfssoftware für Ingenieure. Als ein sich ständig weiterentwickelndes Technologieunternehmen sind wir bestrebt, bestehende Arbeitsabläufe zu erneuern und zu hinterfragen, um Ingenieuren bei ihren Arbeitsprozessen und Entwürfen Zeit zu sparen.