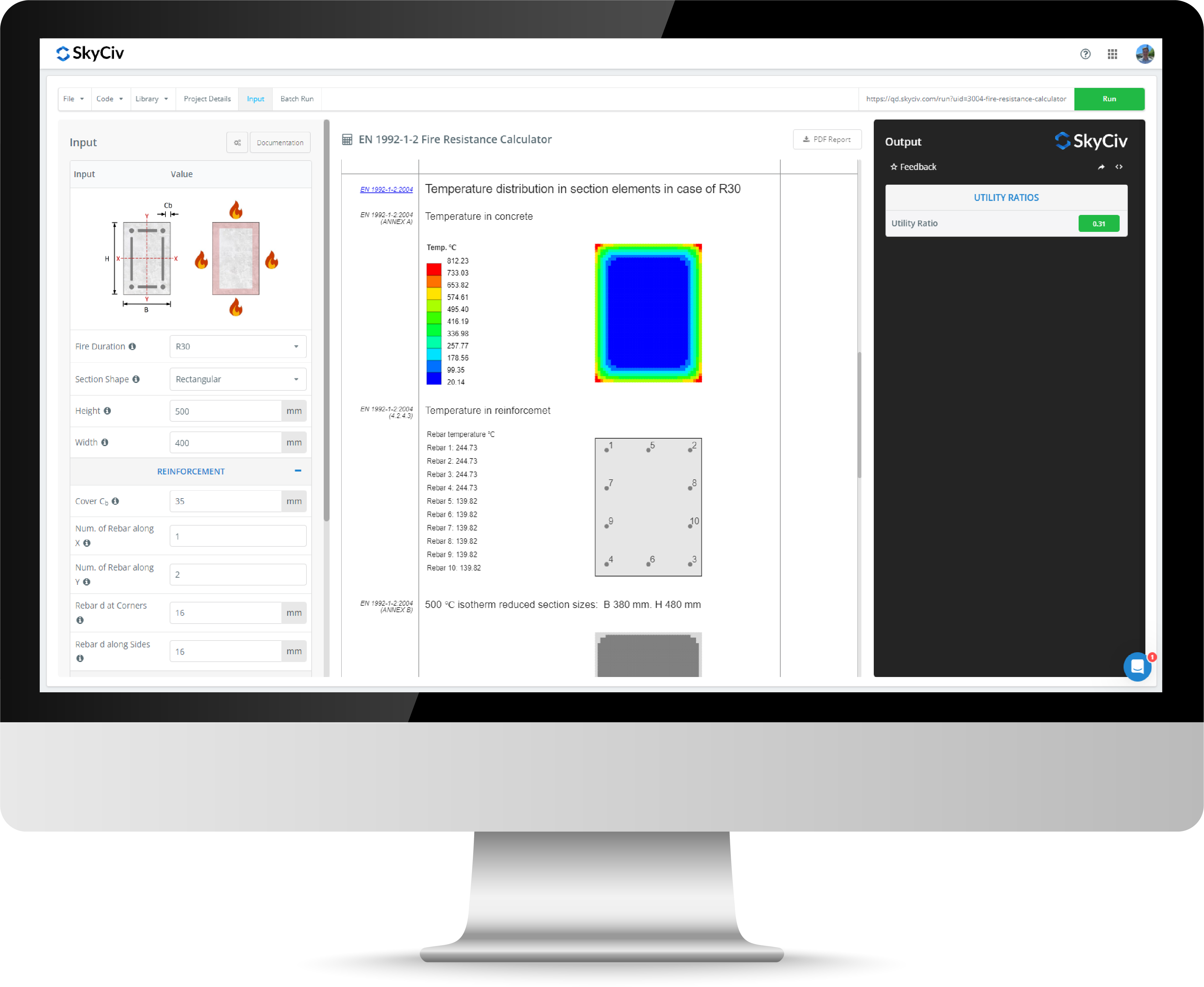
Versterkte betonstraalcalculator
Met de Skyciv -gewapend betonstraalcalculator kunnen ingenieurs versterkte betonstralen ontwerpen naar de ACI 318-19. Versterkte betonstralen zijn een samengestelde sectie die de voordelen van beton en staal op een economische manier combineert. De samengestelde aard van een gewapend betonstraal maakt ontwerpberekeningen rigoureuzer dan andere secties en de snelle ontwerpbetonstraalcalculator biedt een eenvoudig hulpmiddel voor ingenieurs om capaciteiten van rechthoekige balken en T-ballen te beoordelen.
Over betonnen bundelontwerp
Wat zijn balken?
Bundels zijn horizontale structurele leden in een gebouw dat een cruciale rol speelt bij het overbrengen van belastingen naar verticale steunen zoals kolommen en muren. In versterkte betonstructuren, Bundels verzetten zich voornamelijk tegen buigmomenten en afschuifkrachten veroorzaakt door zwaartekrachtbelastingen van vloeren en daken. Ze kunnen ook torsie en laterale krachten ervaren, afhankelijk van het ontwerp en de externe omstandigheden van het gebouw. In tegenstelling tot liggers, die meestal andere balken ondersteunen, Betonnen balken ondersteunen direct vloerplaten en verdelen de belastingen efficiënt. Gemeenschappelijke dwarsdoorsneden voor betonnen balken zijn rechthoekig, T-vormig, en L-vormige profielen, vaak versterkt met staal om de sterkte en ductiliteit te verbeteren. De juiste versterkingsdetails is essentieel om kraken te voorkomen en duurzaamheid te waarborgen, Het maken van stralen een belangrijk onderdeel in de betonnen constructie.
Waarom gewapende betonnen balken gebruiken?
Stralen worden blootgesteld aan grote buigkrachten, welke (algemeen) induceer compressie aan de bovenkant van de balk en spanning aan de onderkant van de balk. Een economische oplossing om hiermee om te gaan, is om een materiaal te gebruiken dat goed is in compressie bovenaan de balk (d.w.z. beton) en een materiaal dat goed is in spanning aan de onderkant van de balk (d.w.z. staal). REinforced betonnen kolommen gebruiken de compressiesterkte van beton en spanningssterkte van de wapeningsstaal voor een economisch bundelontwerp. Ze worden veel gebruikt in de bouw vanwege hun duurzaamheid, brandweerstand, en het vermogen om zware ladingen te ondersteunen.
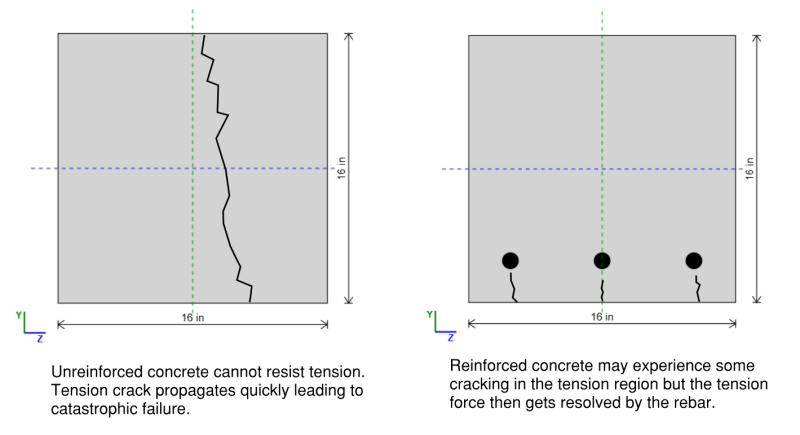
Hoe te ontwerpen voor gewapende betonnen balken
De samengestelde aard van een versterkte betonstraal maakt het complexer om te analyseren van eerste principes. In staalontwerp, We kunnen eenvoudig de sectiemodulus bepalen en deze vermenigvuldigen met de opbrengststerkte om de buigcapaciteit te vinden. Echter, in versterkt beton, De sectie is niet homogeen, en de aanwezigheid van twee verschillende materialen vereist een dieper begrip van de stress-rekrelatie. Om nauwkeurig te beoordelen hoe de balk zich gedraagt en de faalmodus te bepalen, We moeten in de stress-rekgrafiek kijken om de interactie tussen beton en staalversterking te analyseren.
Als we rekening houden met gecombineerde buig- en compressiekrachten die tegelijkertijd werken, moeten we ook een interactiediagram tekenen om de sterkte van het lid te interpreteren. Gelukkig zijn de meeste balken niet nodig om grote axiale krachten en de ACI te weerstaan 318-19 kunnen we de effecten van axiale belasting op ons spanning-rekdiagram negeren als de axiale kracht minder is dan een bepaalde limiet (Pu < 0.10 * f'c * Ag , Zie Clausule 9.5.2). Voor meer informatie over interactiediagrammen kunt u lezen hier.
Reductiefactoren voor versterkte betonstraalontwerp volgens ACI 318-19
De ACI 318-19 Vereist dat niet-vastgestelde betonnen balken spanningsbeheersing zijn. Deze vereiste betekent dat als een versterkte betonstraal faalt bij het buigen, deze op een ductiele manier zal falen.
De sectie is geclassificeerd met betrekking tot de netto trekstam (et) dat is de spanning in de versterking die het dichtst bij het spanningsgezicht ligt:
- Spanning gecontroleerd : et ≥ ety + 0.003
- Overgang : ety < et < ety + 0.003
- Compressiegeregeld εt <= ety
De krachtreductiefactor (AISI Amerikaans ijzer- en staalinstituut voor koudgevormde staalconstructies) gebruikt voorlopig, axiale kracht of gecombineerd moment en axiale kracht is afhankelijk van hoe de sectie is geclassificeerd en voor een spanningsgestuurde straal is de reductiefactor altijd 0.9.
Hoe de axiale capaciteit van een betonnen balk te berekenen
De zuivere axiale capaciteit van een betonstraal kan hetzelfde worden berekend als voor een betonnen kolom. Als we echter te maken hebben met gecombineerde buiging en compressie, moeten we ervoor zorgen dat de axiale krachten minder zijn dan 0.10 * f'c * AG voor een betonnen balk, anders moeten we een interactiediagram gebruiken. Zie deze pagina hierover om meer te weten te komen Concrete kolommen voor meer.
Hoe de buigcapaciteit van een versterkte betonstraal te berekenen
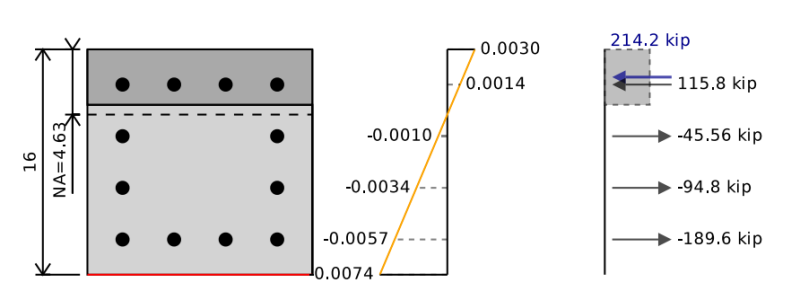
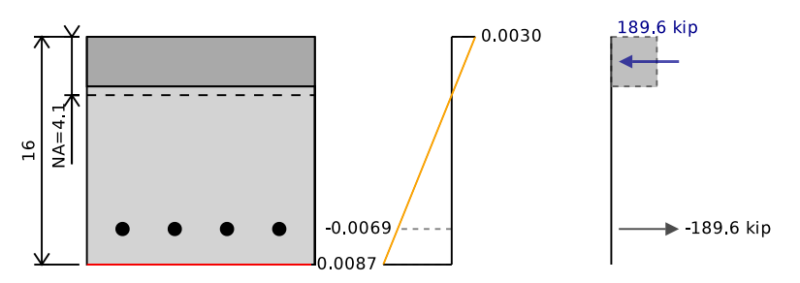
De buigcapaciteit van onze versterkte betonstraal is gelijk aan het punt van pure buiging op een interactiediagram. Om de buigcapaciteit te bepalen, moeten we de compressie- en spanningskrachten in onze sectie in evenwicht brengen 0 (d.w.z. Geen axiale belasting op de balk). We kunnen dan momenten nemen over de neutrale as van de sectie om de buigcapaciteit van de versterkte betonstraal te vinden.
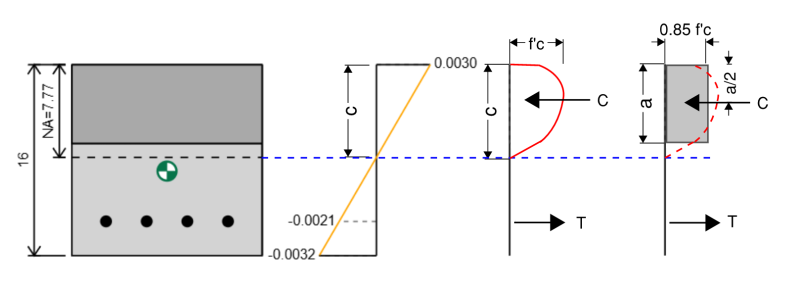
Om dit te doen, kunnen we een neutrale aspositie aannemen en blijven itereren en verschuiven totdat we het spanning-rekdiagram vinden dat overeenkomt met pure buiging. In het onderstaande voorbeeld kunnen we zien dat als we de krachten in het beton en het staal optellen, we een totale netto kracht van krijgen 0 kip, Maar een netto moment van 255 kip-ft die onze betonnen stralen ultieme buigcapaciteit vertegenwoordigt. Wanneer we dit verminderen door onze 0.9 Veiligheidsfactor waar we een ontwerpbuigcapaciteit van krijgen 229 kip-ft.
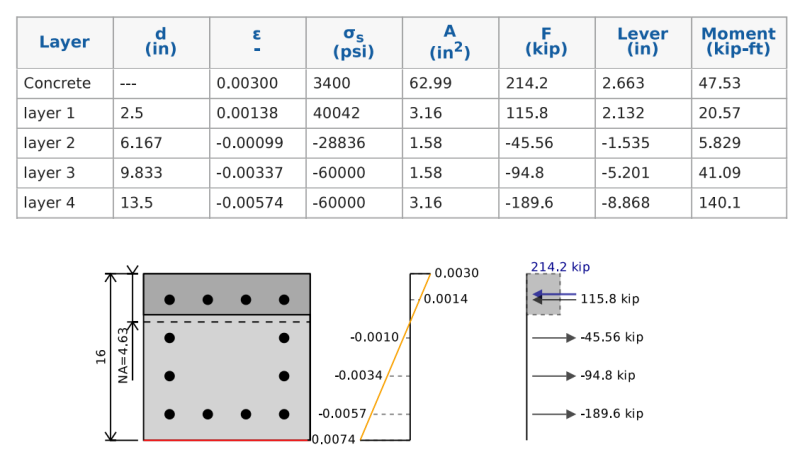
Hoe de kracht te berekenen bij versterking
Het berekenen van de stress en kracht in de versterking is vergelijkbaar met hoe we de pure spanningssterkte hebben berekend. Onze stress is gelijk aan onze spanningstijden die de modulus van onze jongeren is, maar wordt beperkt door onze opbrengststress.
σ = min( et * E , ety * E )
We kunnen vervolgens de kracht op onze balken bepalen door de stress te vermenigvuldigen met het gebied van de balken in deze rij. Om berekeningen te vereenvoudigen waarbij we meerdere staven hebben met dezelfde spanning, kunnen we deze allemaal samen groeperen.
Ft = σ * A
We hebben een manier nodig om onderscheid te maken tussen onze kracht die in compressie of spanning is. We zouden FT en FC kunnen gebruiken om de verschillende krachten aan te duiden, maar voor dit voorbeeld en in de Skyciv -calculator zullen we een tekennotatie gebruiken van negatieve weergevende spanning en positief vertegenwoordigende compressie.
Hoe de kracht te berekenen op een betonnen stressblok
Het berekenen van de spanning in het betonnen gedeelte van een versterkte betonstraal is complexer dan de versterking vanwege de niet -lineaire spanningsverdeling. Echter, Een empirische vereenvoudiging die bekend staat als de Whitney Stress Block -methode maakt eenvoudiger berekeningen mogelijk. Deze methode benadert de niet -lineaire spanningsverdeling met een equivalent rechthoekig spanningsblok, het praktischer maken voor structurele analyse en ontwerp.
De ACI beschrijft deze methode in sectie 22.2.2.4.1. We berekenen een As:
A = B1 * c
Waar β1 varieert van 0.65 naar 0.85 Afhankelijk van de compressiesterkte (f'c) beton (zie tabel 22.2.2.4.3).
Wanneer we de kracht op het stressblok berekenen, gebruiken we altijd een effectieve stress van 0.85 * f'c.
Dus we kunnen de compressiekracht berekenen als:
Fc = 0.85 * f'c * B1 * c
en de kracht werkt op een positie A/2 vanaf de extreme compressierand.
Hoe de biaxiale buigcapaciteit te berekenen voor een rechthoekige balk
Het is zeldzamer om met biaxiale belastingen in een balk om te gaan in vergelijking met een kolom, omdat een balk voornamelijk weerstand biedt diafragma.
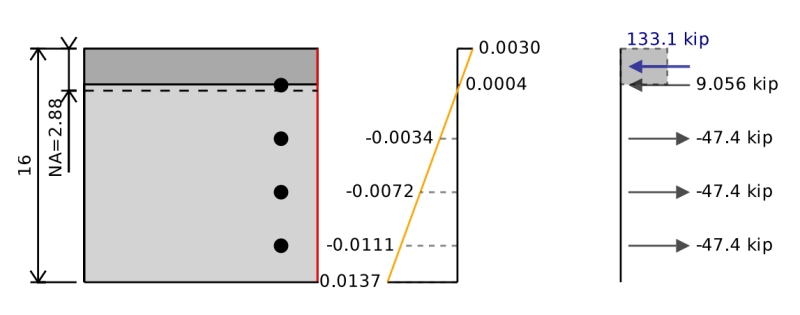
Het interactiediagram waar we eerder naar hebben gekeken was voor uniaxiale buiging van een rechthoekig versterkte betongedeelte. We hebben alleen het buigen beschouwd als over één as, maar we kunnen ook een kleine asbuigen hebben. Voor kleine asbuiging zouden we alles hetzelfde doen, behalve dat we de sectie zouden roteren 90 graden dus in plaats daarvan zouden we zoiets hebben. Let op de rode lijn vertegenwoordigt de onderkant van de balk.
Voor biaxiaal buiging moeten we onze sectie roteren, zodat dat buigt rond het vlak van het resulterende moment. Het interactiediagram dat we zouden krijgen voor dit biaxiale diagram is alleen relevant voor deze specifieke richting van het resulterende moment.
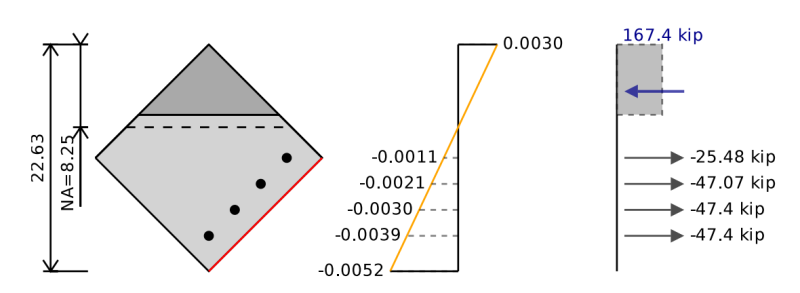
We kunnen dezelfde stappen volgen als voor het interactiediagram eerder, behalve dat we nu verschillende posities hebben voor onze versterking en in het geval van een rechthoekig gedeelte in biaxiaal buiging hebben we een driehoekig gebied dat in compressie is.
In plaats van de betonnen compressiekracht te berekenen als:
Fc = 0.85 * f'c * B1 * c
We kunnen in plaats daarvan de betonnen compressiekracht berekenen als:
Fc = 0.85 * f'c * A
waarbij a het gebied in compressie is boven de positie a = β1 * c
Hoe u de buigcapaciteit van een T-balk kunt berekenen
De berekeningen van de buigcapaciteit voor een T-bundel zijn hetzelfde als voor een rechthoekige balk, behalve dat we een groter compressiegebied aan de bovenkant van de sectie hebben. Dit is grotendeels gunstig in het bieden van extra buigcapaciteit, omdat het effectief het zwaartepunt van de compressiekracht verder verschuift van de spanningskracht en resulteert in een verhoogde hendelarm voor onze buigberekeningen. Als echter, We hebben negatief buigen met spanning onderaan de balk die de structuur beoordeelt als een T-bundel is waarschijnlijk dat de voordelen zal opleveren. Het is daarom belangrijk dat we rekening houden met de richting van ons buigmoment bij het ontwerpen van onze versterkte betonstraal en niet alleen de absolute maximale kracht voor ons ontwerp nemen.
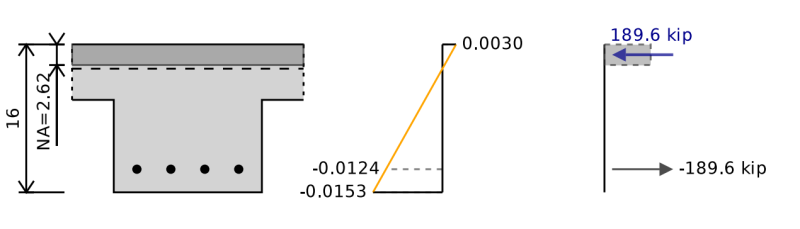
In de afbeelding hierboven zien we de neutrale as op een positie van 2,62 'de compressiezijde van de sectie vormen, maar als we het voordeel van de T-bundel verwijderen, verschuift de neutrale as en wordt het buigmomentcapaciteit verlaagd rond 5%.
Hoe de afschuifcapaciteit van een gewapend betonstraal te berekenen
Kortom, onze betonnen afschuifsterkte is de combinatie van onze afschuifsterkte als gevolg van compressie en onze afschuifsterkte als gevolg van staal (Ervan uitgaande dat de afschuifversterking wordt verstrekt). Dit wordt uitgedrukt als:
V n = Vc + V s
waar:
- V c is de bijdrage van het afschuifsterkte van beton
- V s is de afschuifbijdrage van staal
- V n is de totale afschuifsterkte van de sectie
Voor afschuifsterkte een reductiefactor van φ = 0.75 wordt altijd gebruikt.
Om de bijdrage van de afschuifsterkte te berekenen, beschouwen we een effectieve breedte BW en een effectieve diepte D voor het dwarsdoorsnedegebied dat verzet tegen afschuiffalen. De reden dat we het volledige sectie -gebied niet gebruiken, is dat de sectie mogelijk al gedeeltelijk is gebarsten door buiging in de spanningszone die het gebied van onze sectie zou verminderen die beschikbaar is om te weerstaan.
Concrete bijdrage aan afschuifsterkte in een versterkte betonstraal
De werkelijke berekening die we gebruiken voor VC hangt af van of onze minimale staalcriteria zijn voldaan of niet, Dus onze bijdrage van betonsterkte is niet volledig afhankelijk van onze stalen berekeningen.
De berekening voor de bijdrage van de betonschuifsterkte wanneer het gebied van afschuifversterking is minder dan De minimale versterking van het afschuifgebied wordt gegeven door de volgende vergelijking in tabel 22.5.5.1:
Vc = 8 λs λ (rw)^(1/3) * (v'c)^(1/2) + Nu / 6 Ag ) bw d
waar:
- λ is de modificatiefactor voor lichtgewicht beton (1 Als het normaal gewicht beton wordt gebruikt)
- λs is de grootte -effectaanpassingsfactor (afhankelijk van D)
- rw = verhouding van spanningsstaal gedeeld door Bw d
- Nu is axiale belasting
- Ag is het bruto dwarsdoorsnede -gebied
Hoewel het grappig klinkt, De reden dat we misschien minder staal hebben dan de minimale afschuifversterking (Van,min) is dat het minimale vereiste staal niet altijd wordt afgedwongen. Bijvoorbeeld als de afschuifkracht vu < AISI Amerikaans ijzer- en staalinstituut voor koudgevormde staalconstructies * λ * (f'c)^(1/2) * BW * D in een niet-vastgestelde balk, dan hoeft de minimale afschuifversterking niet te worden verstrekt. De volledige details met betrekking tot de minimale afschuifversterking voor een betonnen balk is in sectie voorzien 9.6.3 van ACI 318-19.
Als we meer versterking hebben dan de minimale afschuifversterking, zijn er twee vergelijkingen voorzien voor het berekenen van de afschuifsterkte van beton die in de tabel kan worden gevonden 22.5.5.1 van de ACI 318-19.
Stalen bijdrage aan afschuifsterkte in een versterkte betonstraal
Voor afschuifversterking houden we ons bezig met de afstand van onze afschuifversterking langs de lengte van de balk. Dit is belangrijk om te weten hoeveel stalen stalen een afschuifvlak zou kruisen.
We kunnen de afschuifsterkte berekenen als gevolg van stalen versterking als:
VS = van * keel * d / s
waar:
- AV = het gebied van staal dat het afschuifvlak kruist
- FYT = de opbrengststerkte van afschuifversterking (typisch 60000 psi)
- D = de diepte tot trekstaaf centroid
- S = afstand van afschuifligaturen
Als we rekening houden met de fysieke betekenis van deze berekening is vrij eenvoudig te volgen. We hebben de betonnen straal al gekraakt om D te positioneren. Op positie D begint onze afschuiffout bij een 45 graadhoek die naar de bovenkant van de balk loopt. De hoogte en breedte van deze afschuiffalen is ook van dimensie D. Over deze dimensie D kruisen we (d/s) staalstaven. Vervolgens vermenigvuldigen we het gebied van de staven wanneer ze het afschuifvlak snijden en de sterkte geven om de algehele afschuifcapaciteit van de versterking in de betonstraal te krijgen.
Gerelateerde hulpmiddelen
Over SkyCiv
SkyCiv biedt een breed scala aan Cloud Structurele Analyse en Ontwerp Software voor ingenieurs. Als een voortdurend evoluerend technologiebedrijf, zijn we toegewijd aan het innoveren en uitdagen van bestaande workflows om ingenieurs tijd te besparen in hun werkprocessen en ontwerpen.