鉄筋コンクリートビーム計算機
SkyCIV鉄筋コンクリートビーム計算機により、エンジニアは鉄筋コンクリートビームをACIに設計できます。 318-19. 鉄筋コンクリートビームは、コンクリートと鋼の利点を経済的に組み合わせた複合セクションです. 鉄筋コンクリートビームの複合性により、設計計算により他のセクションよりも厳密になり、クイックデザインコンクリートビーム計算機は、エンジニアが長方形ビームとTビームの容量を評価するための簡単なツールを提供します。.
コンクリートビームデザインについて
ビームとは何ですか?
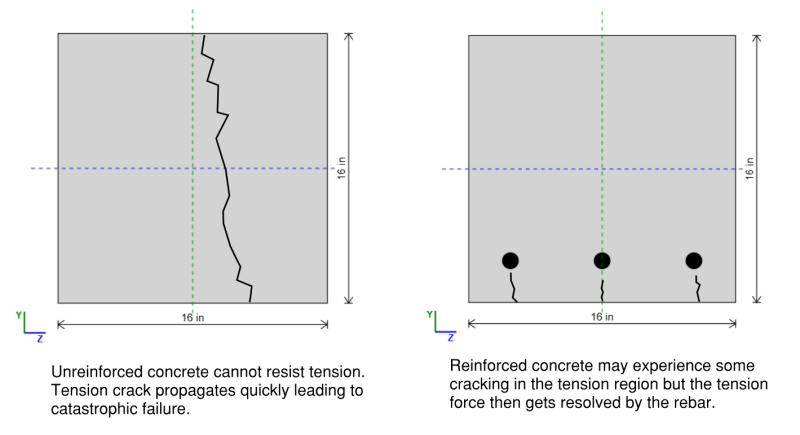
ビームは、列や壁などの垂直サポートに負荷を伝達する上で重要な役割を果たす建物内の水平構造メンバーです. 鉄筋コンクリート構造で, 梁は主に床や屋根からの重力荷重によって引き起こされる曲げモーメントとせん断力に抵抗します. 彼らはまた、建物の設計と外部条件に応じて、ねじれや横方向の力を経験する可能性があります. ガーダーとは異なります, 通常、他のビームをサポートします, コンクリートビームは床スラブを直接サポートし、荷物を効率的に分配します. コンクリートビームの一般的な断面には長方形が含まれます, T字型, およびL字型プロファイル, 多くの場合、強度と延性を高めるために鋼で補強されます. 亀裂を防ぎ、耐久性を確保するためには、適切な強化の詳細が不可欠です, ビームをコンクリート構造の重要なコンポーネントにする.
鉄筋コンクリートビームを使用する理由?
ビームは大きな曲げ力にさらされます, どれの (一般的に) ビームの上部に圧縮を誘導し、ビームの下部に張力を誘導します. これに対処するための経済的解決策は、ビームの上部での圧縮に適した材料を使用することです (つまり. コンクリート) そして、ビームの底で緊張が良好な材料 (つまり. 鋼). Rエインフォームコンクリート柱は、経済的ビーム設計のためにコンクリートの圧縮強度と鉄筋の張力強度を利用しています. それらは耐久性のために建設に広く使用されています, 耐火性, 重い負荷をサポートする能力.
鉄筋コンクリート梁の設計方法
鉄筋コンクリートビームの複合性は、第一原則から分析することをより複雑にします. スチールデザイン, セクションのモジュラスを単純に決定し、曲げ能力を見つけるために降伏強度を掛けることができます. しかしながら, 鉄筋コンクリート, セクションは均一ではありません, そして、2つの異なる材料の存在には、ストレスとストレインの関係をより深く理解する必要があります. ビームがどのように動作するかを正確に評価し、その故障モードを決定する, コンクリートと鉄の補強材との相互作用を分析するには、ストレス - ひずみグラフを調べる必要があります.
曲げ力と圧縮力を同時に作用することを検討する場合は、メンバーの強度を解釈するために相互作用図を描く必要があります. 幸いなことに、ほとんどのビームは、大きな軸方向の力とACIに抵抗するために必要ではありません 318-19 軸方向の力が一定の制限よりも少ない場合、ストレス - ひずみ図に対する軸荷重の影響を無視しましょう (Pu < 0.10 * f'c * Ag , 句を参照してください 9.5.2). 相互作用図の詳細については、読むことができます ここに.
ACIによる鉄筋コンクリートビーム設計の還元因子 318-19
ACI 318-19 プレストレストされていないコンクリートビームが張力制御される必要があります. この要件は、鉄筋コンクリートビームが曲げに失敗した場合、構造が完全に失敗する前に、構造の周りの人々に警告を与える延性方法で失敗することを意味します.
セクションは、正味引張株に関連して分類されます (et) これは、緊張面に最も近い補強の緊張です:
- 緊張が制御されました : et ≥eタイ + 0.003
- 遷移 : eタイ < et < eタイ + 0.003
- 圧縮制御εt <= eタイ
強度削減係数 (ファイ) 今のところ使用されています, 軸方向の力または結合モーメントと軸力は、セクションの分類方法に依存し、張力制御ビームの場合、還元係数は常にです 0.9.
コンクリートビームの軸容量を計算する方法
コンクリートビームの純粋な軸容量は、コンクリート柱と同じように計算できます. ただし、曲げと圧縮を組み合わせて扱っている場合は、軸方向の力がより少ないことを確認する必要があります。 0.10 * f'c * コンクリートビームの場合、それ以外の場合は相互作用図を使用する必要があります. これについて学ぶには、このページを参照してください 詳細については、具体的な列.
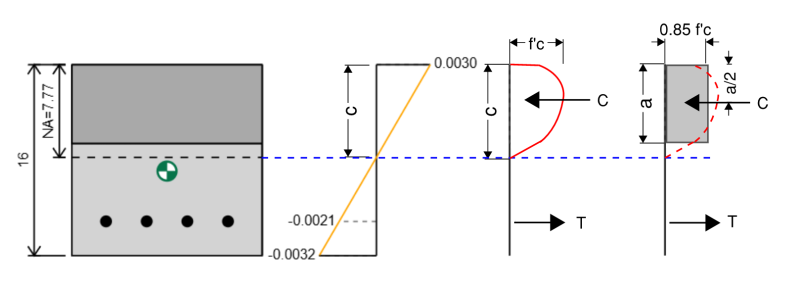
鉄筋コンクリートビームの曲げ能力を計算する方法
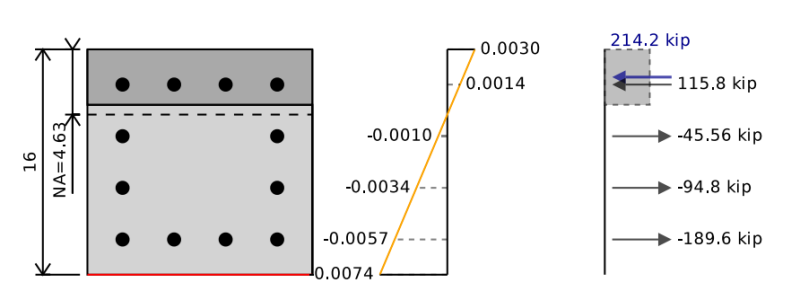
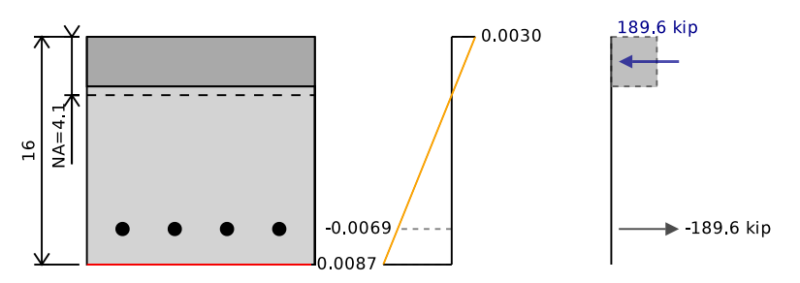
鉄筋コンクリートビームの曲げ能力は、相互作用図に純粋な曲げの点と同等です. 曲げ能力を決定するには、セクションの圧縮力と張力の力のバランスをとる必要があります。 0 (つまり. ビームに作用する軸荷重はありません). その後、鉄筋コンクリートビームの曲げ能力を見つけるために、セクションの中性軸について瞬間をとることができます.
これを行うために、ニュートラルな軸の位置を想定し、純粋な曲げに対応する応力 - ひずみ図が見つかるまで、繰り返してシフトし続けることができます. 以下の例では、コンクリートと鋼の力を合計すると、 0 キップ, しかし、の純瞬間 255 コンクリートビームの最終的な曲げ容量を表すキップフフト. 私たちがこれを私たちによって減らすとき 0.9 安全因子設計曲げ容量を取得します 229 キップフィート.
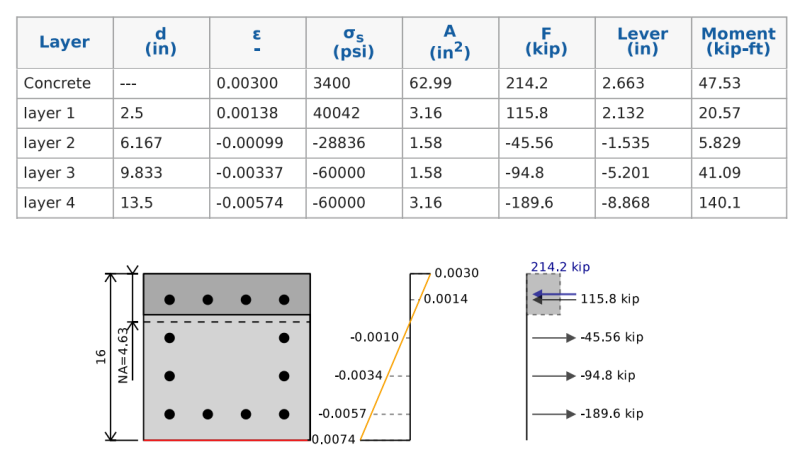
補強の力を計算する方法
補強のストレスと力を計算することは、純粋な張力強度の計算方法に似ています. 私たちのストレスは私たちのひずみ時間に等しいですが、私たちのヤング率は私たちの降伏ストレスによって制限されます.
σ= min( et * E , eタイ * E )
その後、この行のバーの領域をストレスに掛けることで、バーの力を決定できます. 同じひずみのある複数のバーがある場合に計算を簡素化するために、これらすべてをグループ化できます.
ft =σ * あ
私たちは、私たちの力が圧縮または緊張状態にあることを区別する方法が必要です. FTとFCを使用してさまざまな力を示すことができますが、この例ではSKYCIV計算機では、緊張を表す否定的な表記と圧縮を表す正の表記表記を使用します。.
コンクリート応力ブロックの力を計算する方法
鉄筋コンクリートビームのコンクリート部分の応力を計算することは、その非線形応力分布のため、強化よりも複雑です. しかしながら, ホイットニーストレスブロックメソッドとして知られる経験的単純化により、計算を容易にすることができます. この方法は、非線形応力分布に相当する長方形の応力ブロックを近似します, 構造分析と設計のためにそれをより実用的にします.
ACIは、この方法についてセクションで説明しています 22.2.2.4.1. ASを計算します:
A = B1 * c
β1の範囲 0.65 に 0.85 圧縮強度に応じて (f'c) コンクリートの (テーブルを参照してください 22.2.2.4.3).
ストレスブロックの力を計算するとき、私たちは常にの効果的な応力を使用します 0.85 * f'c.
そのため、圧縮力を計算できます:
fc = 0.85 * f'c * B1 * c
そして、力は極端な圧縮エッジからA/2の位置で作用します.
長方形のビームの二軸曲げ能力を計算する方法
ビームは主に重力荷重に抵抗しているため、柱と比較してビーム内の二軸負荷に対処することはまれです。 横隔膜.
私たちが以前に見た相互作用図は、長方形の鉄筋コンクリートセクションの一軸曲げのためのものでした. 私たちは、曲げが1つの軸について起こっているとしか考えていませんが、マイナー軸曲げもすることもできます. マイナー軸曲げの場合、セクションを回転させることを除いてすべてを実行します 90 学位を持っているので、代わりにこのようなものがあります. 注意してください赤い線はビームの底を表します.
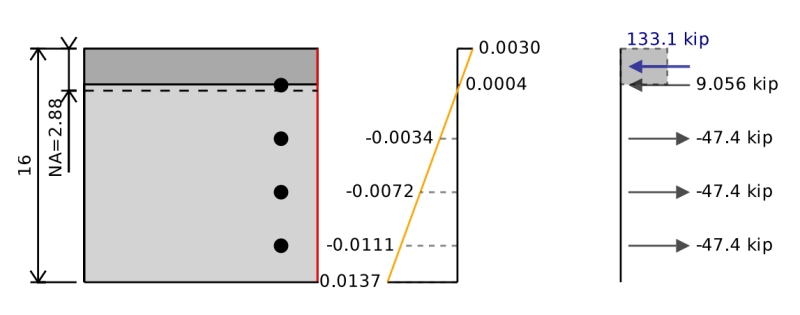
二軸曲げには、結果の瞬間の平面の周りに曲がっているので、セクションを回転させる必要があります. この二軸図に得られる相互作用図は、結果として生じるこの特定の方向にのみ関連しています.
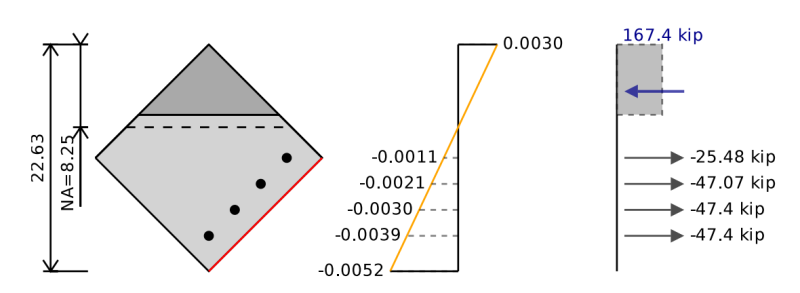
以前の相互作用図で行ったのと同じ手順に従うことができます。これを除いて、補強のための異なる位置があり、二軸曲げの長方形のセクションの場合、圧縮中の三角領域があります。.
コンクリート圧縮力を計算する代わりに:
fc = 0.85 * f'c * B1 * c
代わりに、コンクリート圧縮力を計算できます:
fc = 0.85 * f'c * あ
ここで、Aは位置A =β1の上の圧縮の領域です * c
Tビームの曲げ能力を計算する方法
Tビームの曲げ能力計算は、セクションの上部に大きな圧縮領域があることを除いて、長方形のビームの場合と同じです。. これは、圧縮力の重心を張力からさらにシフトし、曲げ計算のためにレバーアームの増加をもたらすため、余分な曲げ容量を提供する上で主に有益です。. ただし、場合, ビームの底部に張力を伴う負の曲げがあります。Tビームとして構造を評価することは、利点を提供する可能性は低いです. したがって、鉄筋コンクリートビームのために設計するときに曲げ瞬間の方向を考慮し、デザインの絶対的な最大力を単にとらないことが重要です.
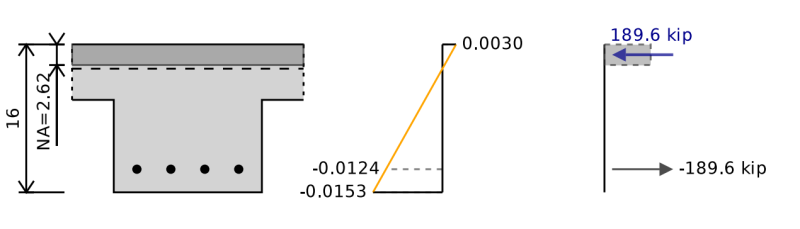
上の画像では、セクションの圧縮側を形成する2.62 'の位置にあるニュートラル軸が表示されますが、Tビームの利点を削除すると、中性軸シフトと曲げモーメント容量が周りで減少します。 5%.
鉄筋コンクリートビームのせん断容量を計算する方法
要するに、私たちのコンクリートせん断強度は、圧縮によるせん断強度と鋼によるせん断強度の組み合わせです (せん断補強が提供されていると仮定します). これはとして表されます:
V ん = Vc + V s
どこ:
- V c コンクリートのせん断強度の寄与です
- V s 鋼のせん断寄与です
- V ん セクションの総せん断強度です
せん断強度の場合、φ=の還元係数 0.75 常に使用されます.
せん断強度の寄与を計算するために、断面領域に有効な幅BWと有効な深さdを考慮しますが、せん断障害に抵抗する. 完全なセクションエリアを使用しない理由は、せん断障害に抵抗するために利用可能なセクションの面積を減らす張力ゾーンでの曲げにより、セクションがすでに部分的に割れている可能性があるためです.
鉄筋コンクリートビームのせん断強度へのコンクリートの寄与
VCに使用する実際の計算は、最小鋼の基準が満たされているかどうかによって異なります, したがって、私たちの具体的な強度の貢献は、鋼鉄の計算から完全に依存しているわけではありません.
せん断補強の面積があるときのコンクリートせん断強度の寄与の計算 未満 せん断領域の最小補強は、テーブルの次の方程式によって与えられます 22.5.5.1:
vc = 8 λs λ (rw)^(1/3) * (f 'c)^(1/2) + Nあなた / 6 あg ) bw d
どこ:
- λは、軽量コンクリートの修正係数です (1 通常の重量コンクリートが使用されている場合)
- λs サイズ効果の変更係数です (dに依存します)
- rw = bで割った張力鋼の比率w d
- Nあなた 軸荷重です
- あg 総断面積です
面白そうですが, 最小のせん断補強よりも少ない鋼があるかもしれない理由 (の,分) 必要な鋼が常に強制されているわけではないということです. たとえば、せん断力vuの場合 < ファイ * λ * (f'c)^(1/2) * bw * d非プレストレスビームでは、最小のせん断補強材を提供する必要はありません. コンクリートビームの最小せん断補強に関する詳細は、セクションに記載されています 9.6.3 ACIの 318-19.
最小のせん断補強材よりも多くの補強がある場合、テーブルにあるコンクリートのせん断強度を計算するための2つの方程式が提供されています。 22.5.5.1 ACIの 318-19.
鉄筋コンクリートビームのせん断強度への鋼の寄与
せん断補強のために、ビームの長さに沿ったせん断補強の間隔に関心があります. これは、せん断平面が交差する鋼鉄の棒の数を知るために重要です.
鋼鉄の補強材のためにせん断強度を計算できます:
vs = of * 喉 * d / s
どこ:
- av =せん断平面と交差する鋼の面積
- FYT =せん断補強の降伏強度 (通常 60000 psi)
- d =引張バー重心までの深さ
- S =せん断靭帯の間隔
この計算の物理的な意味を考慮すると、それに続くのは非常に簡単です. 私たちはすでにdの位置dのために具体的な梁を割っています. 位置Dでは、我々のせん断障害はaから始まります 45 ビームの上部に走行する度角度. このせん断障害の高さと幅も寸法dです. この次元Dを超えて交差します (d/s) 鋼鉄のバー. 次に、バーの領域がせん断平面と交差するときに乗算し、コンクリートビームの補強材の全体的なせん断容量を得るために降伏強度があります.
関連ツール
SkyCivについて
SkyCivは、エンジニアに幅広いCloud Structural Analysis and Design Softwareを提供しています. 常に進化するテクノロジー企業として, 私たちは、既存のワークフローの革新と挑戦に取り組み、エンジニアの作業プロセスと設計の時間を節約します.