Πώς διαφέρει η μη γραμμική ανάλυση καλωδίων από τη γραμμική ανάλυση?

Τα στοιχεία καλωδίων που χρησιμοποιούνται στο δομικό λογισμικό είναι πολύ χρήσιμα όταν αντιμετωπίζουμε καλωδιωτικές γέφυρες, κρεμαστές γέφυρες, καλωδιακά δίχτυα και στύλοι/πύργοι με κουφώματα. Ωστόσο, Τα καλώδια είναι πολύ δύσκολο να μοντελοποιηθούν και να αναλυθούν λόγω των εξαιρετικά μη γραμμικών χαρακτηριστικών τους. Τα καλώδια γενικά μοιάζουν με λεπτά χαλύβδινα σύρματα ή σχοινιά που είναι πολύ εύκαμπτα, συχνά υφίστανται μεγάλες εκτροπές. Για αυτούς τους λόγους, μια γραμμική-στατική ανάλυση δεν είναι κατάλληλη και μπορεί να οδηγήσει σε εξαιρετικά ανακριβή αποτελέσματα.

Στοιχεία καλωδίου αλυσίδων

Ένα καλό λογισμικό δομικής ανάλυσης θα περιλαμβάνει τη δυνατότητα μοντελοποίησης δομών χρησιμοποιώντας ένα αποκλειστικό στοιχείο καλωδίου. Ορισμένα λογισμικά δεν υποστηρίζουν άμεσα στοιχεία καλωδίου, αλλά προτείνουν ότι τα καλώδια μοντελοποιούνται χρησιμοποιώντας μια σειρά από στοιχεία δοκών μόνο με τάση. Ωστόσο, προκειμένου τα στοιχεία ζευκτών να είναι έστω και εξ αποστάσεως ακριβή σε αυτό το σενάριο, Ο χρήστης πρέπει να εισαγάγει τις αρχικές κομβικές θέσεις για να εκτιμήσει το παραμορφωμένο σχήμα του καλωδίου. Όπως μπορεί να φανταστεί κανείς, αυτό γίνεται συχνά δύσκολο έργο σε περίπτωση χαλάρωσης και προέντασης. Επί πλέον, εάν ένας μηχανικός επιχειρήσει να μοντελοποιήσει ένα στοιχείο καλωδίου χρησιμοποιώντας ένα μέλος δοκού με ασθενή καμπτική ακαμψία (Εγώ_με και εγώ_και), τότε η εκτροπή θα είναι μεγάλη χωρίς καμία αύξηση της αξονικής δύναμης όταν εφαρμόζεται εγκάρσια φόρτιση. Προφανώς δεν συμπεριφέρονται έτσι τα καλώδια. Ένα πραγματικό στοιχείο καλωδίου αλυσοειδούς θα λαμβάνει υπόψη την αλλαγή στη γεωμετρία λόγω της εγκάρσιας φόρτισης και "μετατρέπω" αυτή η δράση σε αξονική τάση. Ετσι, ένα μόνο στοιχείο καλωδίου αλυσοειδούς μπορεί να μοντελοποιήσει τη συμπεριφορά ενός καλωδίου με μεγαλύτερη ακρίβεια και ευκολία από ένα στοιχείο δοκού ή πολλαπλά στοιχεία δοκών.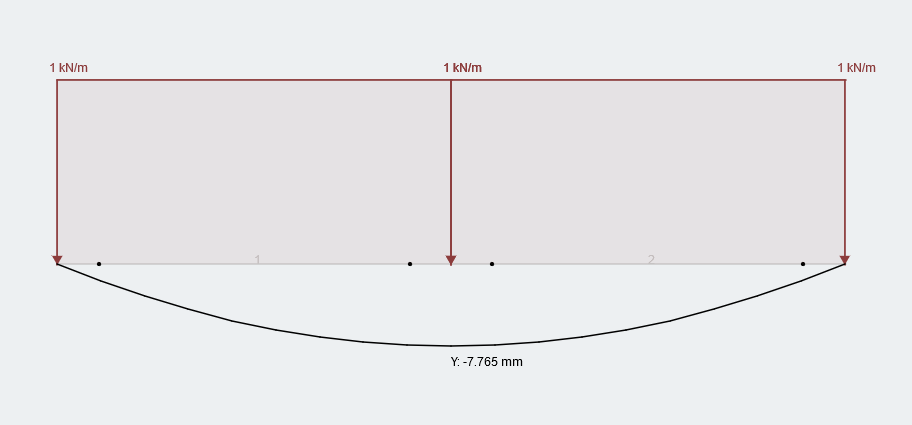

Ένα μοναδικό στοιχείο καλωδίου αλυσοειδούς που παρουσιάζει παραμόρφωση λόγω UDL.

Μοναδικές ιδιότητες των καλωδίων

Τα καλώδια είναι ιδιαίτερα σε αυτό έχουν μόνο αξονική ακαμψία που υποστηρίζει την τάση. Αυτό σημαίνει ότι δεν έχουν κάμψη, ικανότητα διάτμησης ή στρέψης. Επιπροσθέτως, καθώς αυξάνονται τα φορτία των καλωδίων, τείνουν να γίνονται πιο άκαμπτα και είναι σε θέση να υποστηρίξουν μεγαλύτερες ποσότητες.

Πώς ωφελεί τα καλώδια μια μη γραμμική ανάλυση?

Οπως δηλώθηκε παραπάνω, Τα καλώδια είναι γεωμετρικά μη γραμμικά επειδή είναι εξαιρετικά ελαστικά και εύκαμπτα, Επομένως, όταν εμπλέκονται καλώδια, οι μεγάλες παραμορφώσεις είναι κοινές. Σε γραμμική-στατική ανάλυση, οι εξισώσεις ισορροπίας βασίζονται στην απαραμόρφωτη γεωμετρία Ποιες είναι οι συνηθισμένες αστοχίες σε μια δομή boomilever εφαρμόζονται φορτία. Ωστόσο, εάν η παραμόρφωση είναι μεγάλη (όπως όταν υπάρχουν καλώδια), είναι απαραίτητο να εξεταστεί η ισορροπία σε παραμορφωμένες καταστάσεις. Φανταστείτε ότι καθώς εφαρμόζονται φορτία, αλλάζουν κατεύθυνση καθώς η δομή παραμορφώνεται και περιστρέφεται. Μπορείτε να δείτε ένα παράδειγμα αυτού στην παρακάτω εικόνα. Εάν η δοκός παρουσιάσει μικρή παραμόρφωση, τότε η διαδρομή των φορτίων θα παραμείνει σταθερή καθώς η δοκός εκτρέπεται. Ωστόσο, εάν η δοκός εκτρέπεται και περιστρέφεται σημαντικά, τα φορτία γίνονται διαγώνια παρά κατακόρυφα. Τα καλώδια παρουσιάζουν παρόμοια συμπεριφορά όταν παραμορφώνονται και επομένως απαιτείται μια γεωμετρικά μη γραμμική ανάλυση.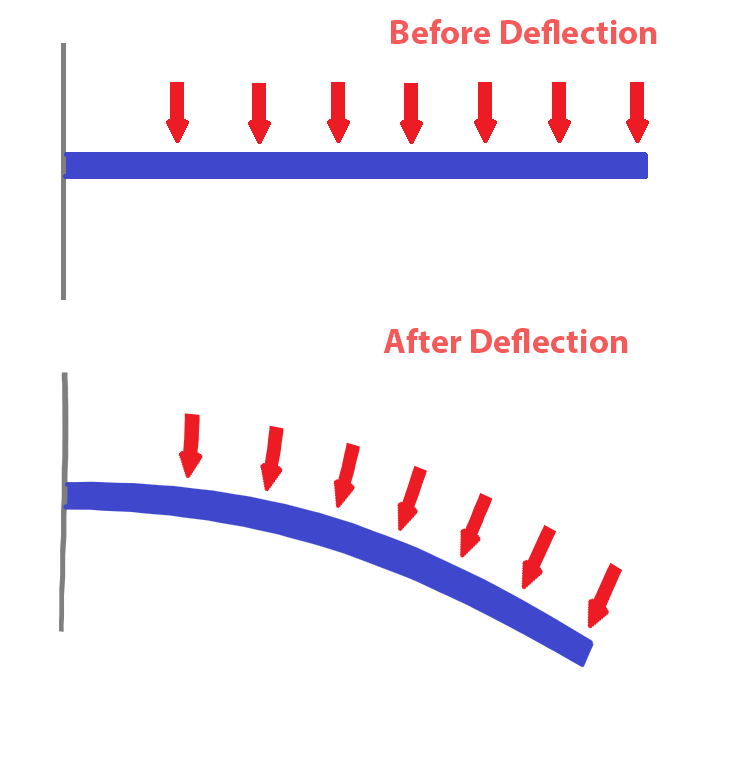

Η κατεύθυνση των φορτίων αλλάζει όταν η εκτροπή είναι μεγάλη, καθιστώντας μια γραμμική-στατική ανάλυση ακατάλληλη.

Η δυσκολία με τη μοντελοποίηση καλωδίων πηγάζει συχνά από ζητήματα σύγκλισης. Οι μη γραμμικές αναλύσεις είναι επαναληπτικές, οπότε η λύση μπορεί να αποκλίνει.

SkyCiv Structural 3D: Καλώδια Catenary

Τα καλά νέα είναι ότι το SkyCiv μπορεί πλέον να αναλύει καλώδια αλυσοειδούς ροής μέσω μη γραμμικής ανάλυσης χρησιμοποιώντας τη θεωρία μεγάλης μετατόπισης. Στην έκδοση 2.1 του SkyCiv Structural 3D, Οι χρήστες θα μπορούν πλέον να μοντελοποιούν καλώδια χρησιμοποιώντας ένα πραγματικό στοιχείο καλωδίου αλυσοειδούς. Οι πελάτες μας μπορούν επίσης να ελέγξουν την προένταση και τη χαλάρωση του καλωδίου καθορίζοντας ένα αρχικό (ή άστρωτο) μήκος καλωδίου.   Ελπίζω αυτό το άρθρο να σας ενημέρωσε σχετικά με την ανάλυση καλωδίων αλυσοειδών και τα μοναδικά χαρακτηριστικά του. Εάν έχετε ερωτήσεις σχετικά με τη μοντελοποίηση ή την ανάλυσή σας, μη διστάσετε να επικοινωνήσετε με την ομάδα υποστήριξής μας!

Δεν έχετε δοκιμάσει το SkyCiv? Ξεκινήστε δωρεάν σήμερα!

ΕΓΓΡΑΦΕΙΤΕ ΔΩΡΕΑΝ