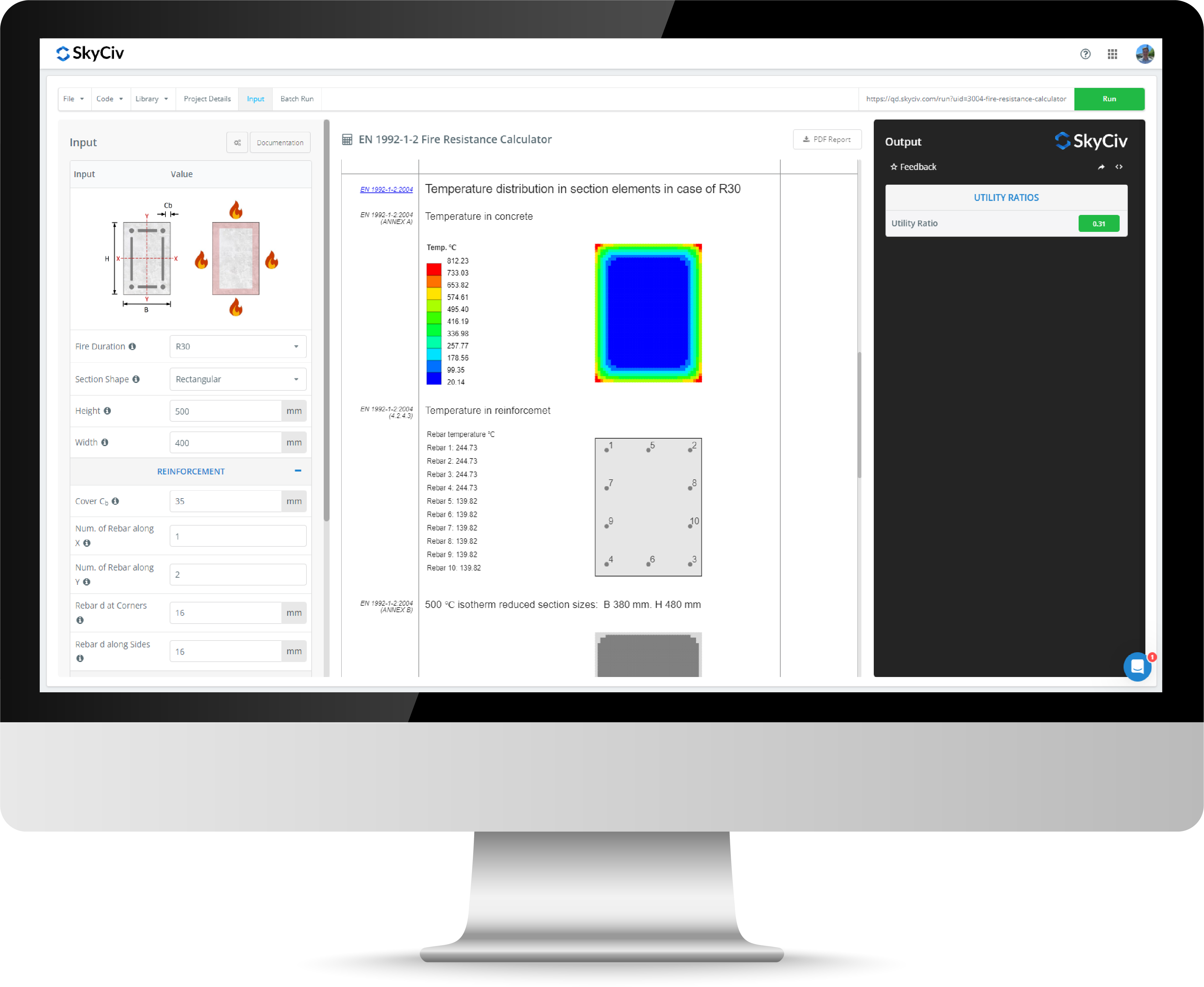
Stahlbeton -Säulenkonstruktionsrechner
Mit dem Säulenrechner mit Skyciv -Stahlbeton können Ingenieure Stahlbeton -Säulendesign für kreisförmige und rechteckige Betonsäulen zu ACI vervollständigen, europäische, und australische Standards. Stahlbetonsäulen sind ein Verbundabschnitt, der die Vorteile von Beton und Stahl auf wirtschaftliche Weise kombiniert. Die zusammengesetzte Natur einer Stahlbetonspalte macht Auslegungsberechnungen strenger als andere Abschnitte, und der Quick -Konstor -Betonspaltenrechner bietet Ingenieuren ein einfach die folgenden Standards:
- den USA - ACI-318-19: Bauvorschriften für Konstruktionsbeton.
- Australische Standards - AS 3600-2018: Australisches Handbuch für Bauingenieure, Stahl & Sehnen.
- Europäische Standards - Eurocode 2: Entwurf von Betonkonstruktionen (IM 1992-1-1:2004).
- Neuseeländische Standards - NZS 3101:2006: Der Entwurf von Betonkonstruktionen
Sie können zwischen diesen Standards in der Wechsel wechseln oben rechts am Betonrechner Verwenden des Flag -Symbols oben auf der linken Eingangsfeld. Um den Rechner auszuführen, Drücken Sie die Schaltfläche „Ausführen“ oben rechts in der Software.
Über konkrete Säulendesign
Was sind Spalten?
Säulen sind vertikale Mitglieder innerhalb eines Gebäudes und sind der Schlüssel, um die Ladung in einem Gebäude zu seiner Fundament zu ermöglichen. Als vertikale Mitglieder, Sie befassen sich hauptsächlich mit großen Kompressionslasten aufgrund von Schwerkraftkräften, aber natürlich aufgrund von Exzentrizitäten bei Beladung und seitlichen Kräften wie Wind- und Erdbebenlasten müssen sie auch den Biegemomenten widerstehen. Säulen sind den Stapeln ziemlich ähnlich, außer dass Stapel Erde haben, um sich gegen das Knicken zurückzuhalten, und können Kräfte entlang des Stapels lösen, wo sich eine Säule an seiner Basis widersetzt. Pfähle haben fast immer einen kreisförmigen Abschnitt, aber Betonsäulen haben üblicherweise kreisförmige oder rechteckige Querschnitte.
Warum konkrete Spalten verwenden?
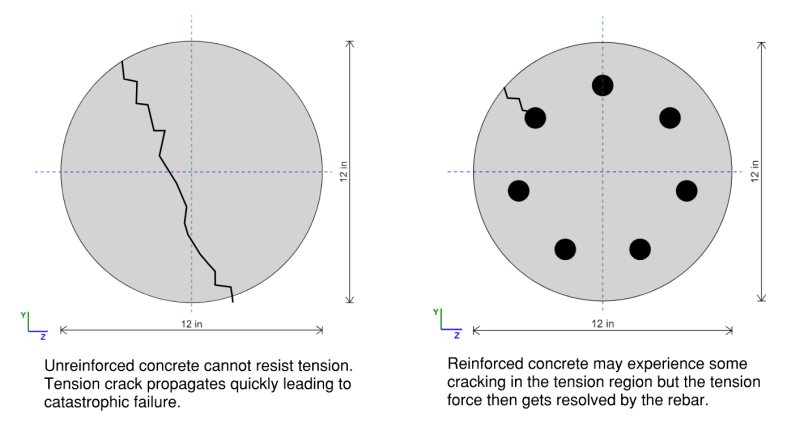
Säulen sind großen Komprimierungskräften ausgesetzt, die uns natürlich dazu bringen, Beton zu verwenden, Eine sehr wirtschaftliche Lösung für den Umgang mit Kompressionslasten. Unglücklicherweise, Einfacher Beton ist spröde und schwach in Spannung und Biegung machen es unsicher, ohne Stahlverstärkungsstangen zu verwenden (Bewehrung).
Stahlbetonsäulen verwenden die Kompressionsstärke von Beton und Spannungsstärke von Bewehrungsstärke für eine wirtschaftliche Säulendesign. Betonsäulen werden aufgrund ihrer Haltbarkeit häufig im Bau verwendet, Feuerwiderstand, und Fähigkeit, schwere Lasten zu unterstützen.
So entwerfen Sie für Stahlbetonspalten
Die zusammengesetzte Natur einer verstärkten Säule macht es schwieriger, aus den ersten Prinzipien zu analysieren. Mit Stahl können wir einfach den Abschnittsmodul berechnen und diese durch die Ertragsfestigkeit multiplizieren, um eine Biegerkapazität zu finden. Mit Stahlbeton ist der Abschnitt nicht homogen und mit zwei verschiedenen Materialien müssen wir uns mit dem Stress-Dehnungs-Diagramm befassen, um wirklich zu sehen, was passiert und wie unser Abschnitt möglicherweise scheitern kann.
Dies wird schwieriger, wenn wir bedenken. Ein Werkzeug, das bei einem solchen Design hilft, ist das, was als Interaktionsdiagramm bezeichnet wird.
Was ist ein Interaktionsdiagramm ?
Ein Wechselwirkungsdiagramm ist eine grafische Darstellung der Festigkeitskapazität einer Säule unter kombinierten Biege und axialen Lasten.
In den folgenden Abschnitten dieses Artikels wird beschrieben, wie das Wechselwirkungsdiagramm für eine verstärkte Spalte von Hand berechnet wird. Nach den Prinzipien zur Erzeugung des Interaktionsdiagramms wird der Leser ein besseres Verständnis der wichtigsten Punkte in einem Interaktionsdiagramm und die Interpretation der Ergebnisse des Interaktionsdiagramms für ein konkretes Säulendesign hinterlassen.
Das Generieren eines Interaktionsdiagramms von Hand für jeden Spaltenabschnitt kann zeitaufwändig sein, sodass Software wie der Skyciv -Betonspaltenrechner vorhanden ist Diagramm.
So erstellen Sie ein Interaktionsdiagramm
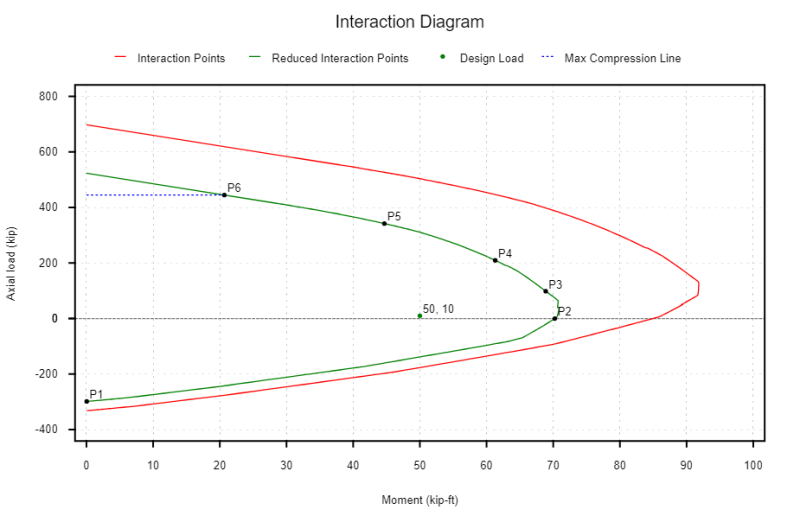
Bei der Erstellung eines Interaktionsdiagramms werden die Säule der Stahlbeton für die folgenden Fälle bewertet:
- (Ein Rundgang durch die Berechnungen, die zum Entwerfen eines kombinierten Fundaments erforderlich sind) Reine Spannung - Dies ist die größte axiale Zuglast, die die Säule tragen kann.
- (Ein Rundgang durch die Berechnungen, die zum Entwerfen eines kombinierten Fundaments erforderlich sind) Reines Biegen - Der Abschnitt unterliegt einem Biegemoment m und einer axialen Kraft von p = 0
- (P3) Ausgeglichener Punkt (et = ety) - Ein ausgewogener Zustand wird erreicht, wenn ein Betonversagen gleichzeitig mit dem Ausbeuten des extremen Zugstahls auftritt.
- (P4) Halbzielpunkt (et = 0.5 ety) - Dies ist eine Zwischenposition, um ein genaues Interaktionsdiagramm zu zeichnen.
- (P5) Dekompressionspunkt (et = 0) - Dieser Fall markiert die Position, wenn Spannungsrundenspleiße zu Kompressionsrundenspleißen wechseln (ACI). Balken wechseln zwischen einigen Spannungskräften, um nur Kompressionskräfte zu übernehmen.
- (P6) Reine Komprimierung - Dies ist die größte axiale Druckbelastung, die die Säule tragen kann.
Unser Interaktionsdiagramm kann auch den in unserem Design erforderlichen Sicherheitsreduzierungsfaktor berücksichtigen. Etwas, das wir im obigen Wechselwirkungsdiagramm bemerken, ist, dass wir einen größeren Sicherheitsfaktor in der kompression kontrollierten Region haben (0.65 oder 0.75) als wir in der spannungsgesteuerten Region tun (0.9).
Reduktionsfaktoren für die Konstruktion von Betonspalten nach ACI 318-19
Der Festigkeitsreduktionsfaktor (Phi) für den Moment verwendet, Axiale Kraft oder kombiniertes Moment und axiale Kraft hängen davon ab, wie der Abschnitt klassifiziert wird.
Der Abschnitt wird in Bezug auf die Net -Zugstrecke klassifiziert (et) Welches ist die Belastung in der Verstärkung, die dem Spannungsgesicht am nächsten liegt:
- Mit Spannung kontrolliert : et ≥ ety + 0.003
- Übergang : ety < et < ety + 0.003
- Kompression kontrolliert εt <= ety
Aufgrund der Änderung des Festigkeitsreduktionsfaktors kann es auch nützlich sein, den Kompressionskontrollpunkt zu berechnen (P3 im vorherigen Diagramm) und der Spannungskontrollpunkt (et ≥ ety + 0.003) nicht beschriftet.
Es hängt auch von unserer Querverstärkung ab. Für Spiralen, die bestätigt werden 25.7.3 Wir können PHI basierend auf unserem ε bekomment wie:
- Mit Spannung kontrolliert: φ = 0.9
- Kompression kontrolliert: φ = 0.75
- Übergang: φ = 0.75 + 0.15 (et - ety ) / 0.003
Für andere Arten von Querverstärkung:
- Mit Spannung kontrolliert - φ = 0.9
- Kompression kontrolliert - φ = 0.65
- Übergang = φ = 0.65 + 0.25 (et - ety ) / 0.003
(Tatsächlich ist die Übergangsformel eine einfache lineare Funktion, die davon abhängt, wie nahe wir uns an den Komprimierung oder den Spannungsregelpunkt sind.)
So berechnen Sie die reine Kompressionskapazität einer Betonspalte
Die reine Kompressionskapazität oder die Kürbislast ist die Stärke der Säule unter reiner axialer Belastung.
Mit dem ACI 318-19 Sektion 22.4.2 Wir können die reine Kompressionslast für eine Betonspalte unter Verwendung der folgenden Formel berechnen:
P0 = 0.85 f'c * (EinG - Einst) + fj * Einst
wo:
- f'c ist die Betonkompressionsstärke
- fj Ist die Rendite der Bewehrung
- EinG ist die Bruttofläche des Abschnitts
- Einst ist die Gesamtfläche der Stahlbewusstsein
- (EinG - Einst) ist der effektive Querschnittsbereich von Beton.
Dieser Punkt entspricht der oben links im Wechselwirkungsdiagramm ohne einen angewandten Festigkeitsreduktionsfaktor. Wir können diesen Wert durch unseren Festigkeitsreduktionsfaktor für den kompression kontrollierten Bereich verringern (Da wir in reiner Kompression sind). Der ACI 318-19 Die maximale Grenze über die durch die gestrichelte Blaulinie angegebene maximale Grenze jedoch auferlegt und im nächsten Abschnitt abgedeckt wird.
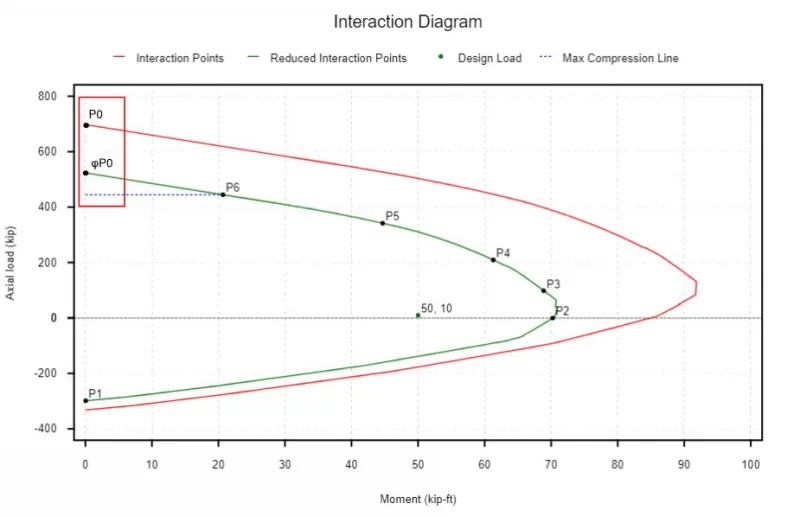
Berechnung der maximal zulässigen Kompressionskapazität einer Betonspalte (ACI)
Für zufällige Exzentrizität das ACI zu berücksichtigen 318-19 begrenzt die maximal zulässige Kompressionskomposition einer Stahlbetonspalte auf 80 zu 85 Prozent der im vorherigen Abschnitt berechneten reinen nominalen Kompressionskapazität.
Die Reduzierung hängt von der Art des Mitglieds und der in der Säule verwendeten Querverstärkung ab (Siehe Tabelle 22.4.2.1 von ACI 318-19).
Im Allgemeinen haben wir das Folgende, wo die Querverstärkung Krawatten ist:
- P.n,max = 0.80 * P0
Oder wenn die Querverstärkung Spiralen ist:
- P.n,max = 0.85 * P0
So berechnen Sie die reine Spannungskapazität einer Betonspalte (ACI)
Die Spannungsstärke der Stahlbetonsäule erfolgt ausschließlich aus der Stärke der Verstärkung und ist proportional zu dem Bereich der Verstärkung, den wir haben.
Die Formel zur Berechnung der axialen Spannungsstärke einer Stahlbetonspalte ist einfach:
P.nt,max = fj * Einst
&
P1 = φ * P.nt,max
Da sich der Abschnitt in reiner Spannung befindet und alle unsere Balken als den Abschnitt ergeben, ist der Abschnitt kontrolliert und der Festigkeitsreduktionsfaktor φ immer ist 0.9.
Berechnung der Gleichgewichtspunktkapazität einer Betonspalte
Der Gleichgewichtspunkt ist definiert als die Belastung, die dazu führtt = ety im selben Moment, in dem der Beton ergibt. Die Methode zur Berechnung der Säulenstärke (Für Biege und axiale Kompression oder Spannung) Zu diesem Zeitpunkt entspricht die Methode, die für andere Punkte mit einem bestimmten ε verwendet wirdt (d.h.. εt = 0, et = 0.5 εy).
Wir können zuerst die Ertragsdehnung der Verstärkung unter Verwendung des Hookes -Gesetzes berechnen:
εty = fj / E.
Für ein 60 KSI -Bar mit einem Jungmodul von 29000 KSI Wir haben eine Ertragsstamm von
εty = 60/290000 = 0.00207
Wir nehmen auch immer die Ertragsdehnung für Beton ein 0.003 (in Abschnitt definiert 22.2.2.1 von ACI 318-19).
Mit diesen beiden Werten können wir unser Dehnungsdiagramm zeichnen und auf dem Dehnungsdiagramm basieren, können wir die Spannungen in unserem Abschnitt bestimmen. Die Berechnung von Spannungen ist in den nächsten beiden Abschnitten behandelt.
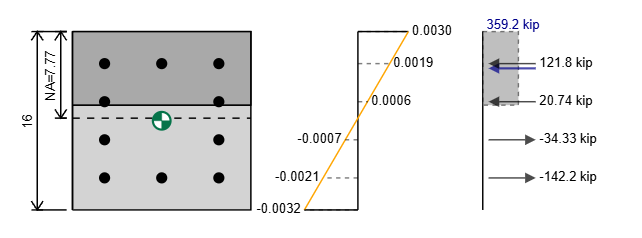
So berechnen Sie die Kraft der Verstärkung in der Betonspalte
Die Berechnung der Spannung und Kraft in der Verstärkung ähnelt der Art, wie wir die reine Spannungsstärke berechnet haben. Unser Stress entspricht unseren Belastungszeiten unseres Jungmoduls, aber durch unseren Ertragsstress begrenzt.
σ = min( et * E. , ety * E. )
Wir können dann die Kraft auf unseren Balken bestimmen, indem wir den Stress mit dem Bereich der Stangen in dieser Reihe multiplizieren. Um Berechnungen zu vereinfachen, bei denen wir mehrere Balken mit dem gleichen Belastung haben, können wir diese alle zusammen gruppieren.
Ft = σ * Ein
Wir brauchen eine Möglichkeit, zwischen unserer Kraft in Kompression oder Spannung zu unterscheiden. Wir könnten FT und FC verwenden, um die verschiedenen Kräfte zu bezeichnen, aber für dieses Beispiel und im Skyciv -Rechner werden wir eine Vorzeichenbeschreibung der negativen Spannung und der positiven Komprimierung verwenden.
Wie berechnet man die Kraft auf einem Betonspannungsblock
Die Berechnung der Spannung der Betonkomponente unserer Stahlbetonspalte ist etwas komplizierter, da die Spannungsverteilung für einen Betonabschnitt nicht linear ist und stattdessen ungefähr parabolisch ist. Glücklicherweise, Es gibt eine empirische Vereinfachung für die Berechnung von Spannungen auf dem konkreten Abschnitt, der als Whitney -Stressblockmethode bekannt ist. Bei dieser Methode approximieren wir die parabolische Spannungsverteilung als einen rechteckigen Spannungsblock.
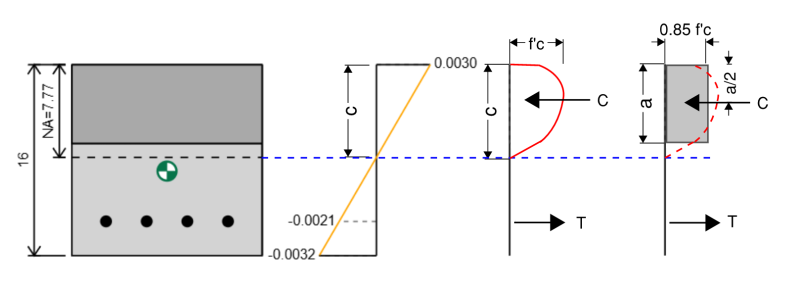
Das ACI beschreibt diese Methode im Abschnitt 22.2.2.4.1. Wir berechnen a as:
A = B1 * c
wo β1 reicht von 0.65 zu 0.85 Abhängig von der Kompressionsstärke (Die Scherfestigkeit entspricht einer kombinierten Schertragfähigkeit des Betons und der Stahlbewehrung) von Beton (Siehe Tabelle 22.2.2.4.3).
Wenn wir die Kraft auf dem Spannungsblock berechnen, verwenden wir immer einen wirksamen Stress von 0.85 * Die Scherfestigkeit entspricht einer kombinierten Schertragfähigkeit des Betons und der Stahlbewehrung.
So können wir die Kompressionskraft als berechnen:
Fc = 0.85 * Die Scherfestigkeit entspricht einer kombinierten Schertragfähigkeit des Betons und der Stahlbewehrung * B1 * c
und die Kraft wirkt an einer Position A/2 aus der extremen Komprimierungskante.
So berechnen Sie die axiale Kapazität einer Betonsäule aus einem Spannungs-Dehnungs-Diagramm
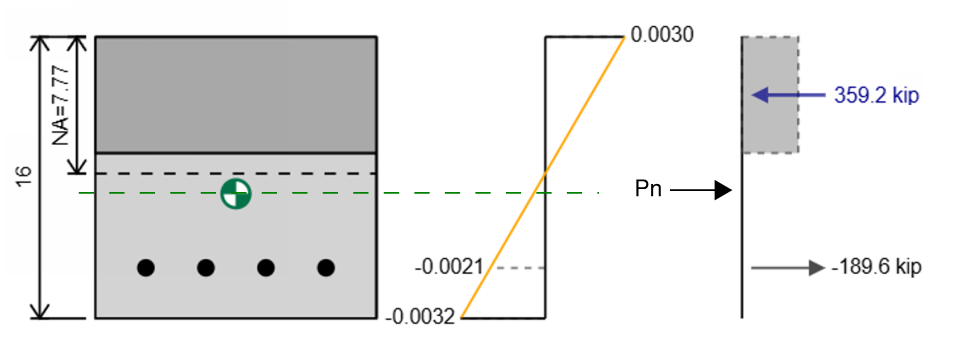
Wir haben jetzt alle Stämme, Spannungen und Kräfte auf der Verstärkung und Beton in unserem Abschnitt, aber wir haben immer noch nicht angegeben, wie die axiale Kapazität oder die Biegekapazität für diesen Abschnitt ist.
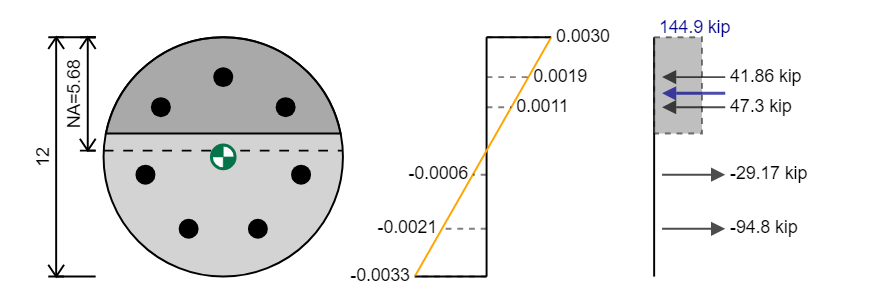
Die axiale Kapazität ist die resultierende Kraft und die Position, in der sie wirkt (Grüner Zentroidmarker im Diagramm). Im obigen Beispiel ist die axiale Kapazität
Mit der PrinciStatikples Wir können unser Kraftdiagramm verwenden, um die Kapazität unseres Abschnitts zu bestimmen. Zuerst können wir die Kräftesumme verwenden, um die axiale Kapazität zu bestimmen, Zu wissen, dass unsere Gesamtkomprimierungskräfte unserer Gesamtspannung gleich sein müssenCES.
Σfx = 0 → σc = σt
Wir können dann die Stahlkompressionskräfte und die Beton -Druckkraft und die Stahlspannungskräfte zusammenfassen, um die resultierende Kraft herauszufinden, die die axiale Kapazität unseres Abschnitts ist.
Pn = σc - Σt
Zum Beispiel wenn wir haben 359.2 Kip der Komprimierung und 189.6 Kip der Spannung Für den Abschnitt ist die resultierende Kraft 359.2 - 189.6 = 169.6 kip. Beachten Sie, dass die gezogene Kraft, die den Abschnitt vollständig ausgleichen würde (dh eine Spannungskraft von 169.6) ist das Gegenteil der Kapazität, die ist 169.6 Kip in Komprimierung, da wir können
So berechnen Sie die Biegekapazität einer Betonsäule aus einem Spannungs-Dehnungs-Diagramm
Wir wissen jetzt, dass wir eine Kraft benötigen, die auf unseren Abschnitt wirkt, um sie auszugleichen. Diese Kraft wirkt am Kunststoff -Schwerpunkt des Abschnitts, der in der obigen Zeichnung durch den Green Centroid -Marker gekennzeichnet ist.
Um das Kunststoff -Schwerpunkt zu ermitteln, sind die Berechnungen übereinstimmend wie bei a Normale Zentroidberechnung Außer anstatt eine um einen Abstand zu multiplizieren, sind wir mehrere F um eine Entfernung.
Um die Biegerkapazität zu berechnen, können wir Momente über jede Position einnehmen, und wir werden einen Nettoomoment bekommen. Wir können die Momente über die Position des Plastik -Schwerpunkts einnehmen, also müssen wir uns dann keine Sorgen um die Kraftpnn in unseren Berechnungen machen, da sein Hebel wäre 0. Eine Tabelle kann für diese Berechnungen hilfreich sein, insbesondere wenn wir viele Verstärkungsschichten haben.

Wir können sehen, dass die Berechnungen für unsere Momentkapazität sind
Mn = Σf x Hebel = 359.2 x 5.615/12 + -189.6 x -4.206/12 = 168.1 + 66.5 = 234.6 kip-ft
Ein positiver Moment bedeutet, dass sich die Oberseite des Abschnitts in Komprimierung befindet und der Boden des Abschnitts in Spannung ist.
So berechnen Sie die reduzierte Biege- und Axialkapazität der Betonsäule
Wir haben eine Momentkapazität von berechnet 234.6 KIP-ft und eine Kompressionskapazität von 169.6 KIP, dies sind jedoch unsere endgültigen Kapazitäten und müssen durch einen Festigkeitsreduktionsfaktor reduziert werden.
Da wir derzeit den Gleichgewichtspunkt in Betracht ziehen und εt = εty sind, dann befinden wir uns im kompression kontrollierten Bereich und müssen einen Sicherheitsfaktor verwenden 0.65 oder 0.75 Abhängig von der Querverstärkung in der Säule der Stahlbeton.
Aufteilung eines Interaktionsdiagramms
Bisher haben wir gesehen, wie man berechnet
- (Ein Rundgang durch die Berechnungen, die zum Entwerfen eines kombinierten Fundaments erforderlich sind) Reiner Spannungspunkt
- (P6) Reiner Komprimierungspunkt
- (P3) Ausgeglichener Punkt
Verwenden des gleichen Verfahrens wie die Berechnung für den ausgewogenen Punkt können wir auch die axiale und biege Kapazität berechnen:
- (P4) Halbzielpunkt
- (P5) Dekompressionspunkt
Der Unterschied zwischen diesen drei Punkten (P3, P4, P5) ist einfach die anfängliche Annahme, die wir bei der Erzeugung des Dehnungsdiagramms machen, wobei jeder Schritt nach demselben ist.
Mit diesen fünf Punkten ermittelten, für den wir nicht berechnet haben, ist der reine Biegepunkt. Dieser Punkt entspricht dem Punkt, an dem wir PN = haben 0 in unserem Abschnitt. Um diesen Punkt zu bestimmen, erfordern wir eine iterative Lösung, bei der wir eine Position einer neutralen Achse erraten (Wert von C in ACI) und bestimmen, ob pn = 0. Sobald wir diese Position der neutralen Achse gefunden haben.
Bei jedem Wert können wir dann ein Wechselwirkungsdiagramm für unsere Säule der Stahlbeton erzeugen. Wir können einfach unsere Schlüsselpunkte zeichnen und eine gerade Linie zwischen ihnen zeichnen, um ein einfaches Interaktionsdiagramm zu erstellen. Mit Software wie dem Skyciv Quick Design Concret Column Calculator können wir im Interaktionsdiagramm viele weitere Punkte erzeugen, anstatt nur die wichtigsten Punkte, die als glatteres und genauereres Diagramm ergeben können.
Ein weiterer Punkt, der beim Entwerfen des ACI nützlich sein kann 318-19 ist der Übergangspunkt der Spannungssteuerung, da sich der Phi -Faktor so verändert. Beachten Sie auch, dass die maximal zulässige reine Kompressionskraft eine Verringerung der maximal zulässigen Kraft vorliegt (Bezeichnet durch die blaue Linie) Die maximale Kompressionskraft kann auch einer Momentkapazität widerstehen, die nach Punkt P6 in der folgenden Grafik bezeichnet wird.
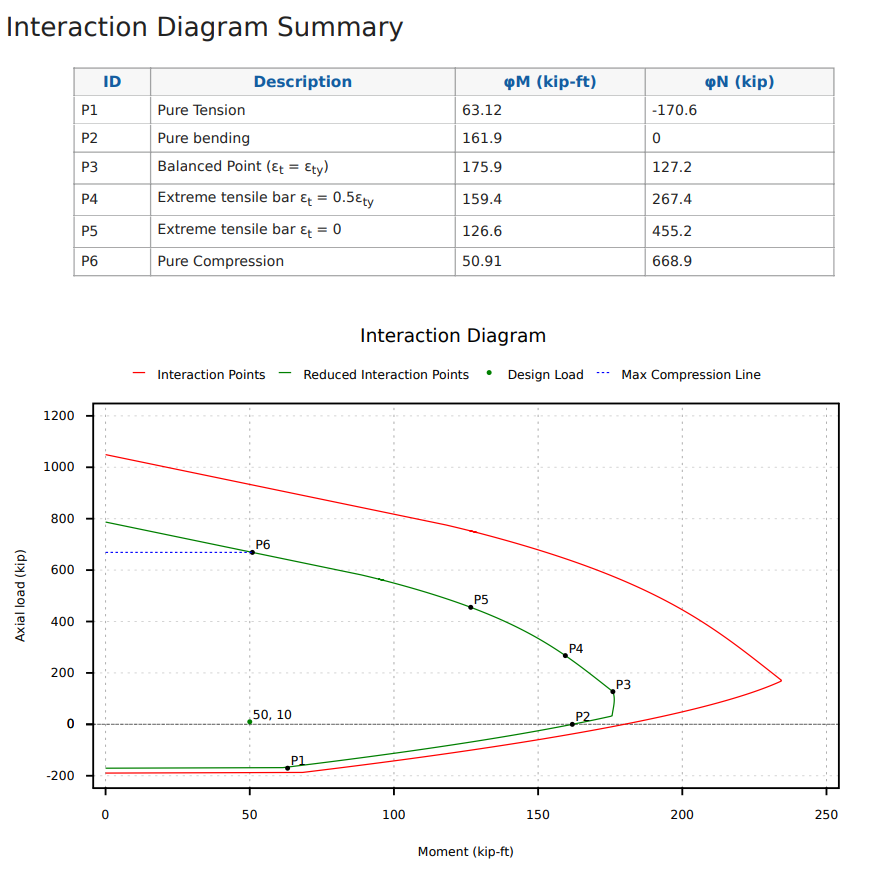
So lesen Sie ein Interaktionsdiagramm?
Bisher haben wir viel darüber gelernt, wie wir ein Interaktionsdiagramm erstellen können, aber wie können wir es in unserem Design verwenden und warum ist es notwendig.
Letzten Endes, Das Interaktionsdiagramm ist nützlich, da es für unseren Abschnitt immer gleich gleich ist (Biegen in eine bestimmte Richtung Biegen) und hängt nicht von den Variationen unserer axialen Kraft und unserem Moment ab.
Wenn wir nur berechnen würden, wenn unser Abschnitt eine Kapazität für eine einzelne axiale Kraft und eine Momentkombination hatte.
Das Interaktionsdiagramm bietet Verwendung mit einem visuellen Tool, mit dem wir schnell feststellen können, ob eine bestimmte Lastkombination den Anforderungen des von uns verwendeten Entwurfsstandards wie dem ACI erfüllt 318-19. Alles, was wir tun müssen, ist unseren Punkt zu zeichnen und sicherzustellen, dass es sich im Bereich unseres Interaktionsdiagramms befindet, Und wir konnten viele verschiedene Lastkombinationen gleichzeitig zeichnen.
Nutzungsverhältnisse sind geringfügig willkürlich, da wir uns hauptsächlich darum befassen, wenn wir uns im Bereich befinden oder nicht, Wir können jedoch die Nutzungsverhältnisse dadurch definieren, wie weit wir von einer bestimmten Grenze entfernt sind. Unser Abstand in der X -Achse ist unsere Momentauslastung für das Interaktionsdiagramm und unser Abstand in der Y -Achse ist unsere axiale Auslastung für das Interaktionsdiagramm.
So erstellen Sie ein Interaktionsdiagramm für das biaxiale Biegen auf einer Betonspalte
Das Wechselwirkungsdiagramm, das wir uns zuvor angesehen haben. Wir haben die Biegung nur für eine Achse in Betracht gezogen, aber wir könnten auch eine kleinere Achsenbiegung haben. Für eine kleinere Achsenbiegung würden wir alles gleich tun, außer dass wir den Abschnitt drehen würden 90 Grad, also hätten wir stattdessen so etwas.
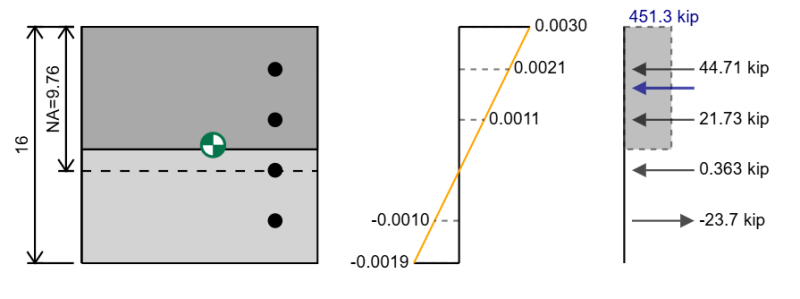
Für die biaxiale Biegung müssen wir unseren Abschnitt drehen. Das Interaktionsdiagramm, das wir für dieses biaxiale Diagramm erhalten würden, ist nur für diese besondere Richtung des resultierenden Moments relevant.
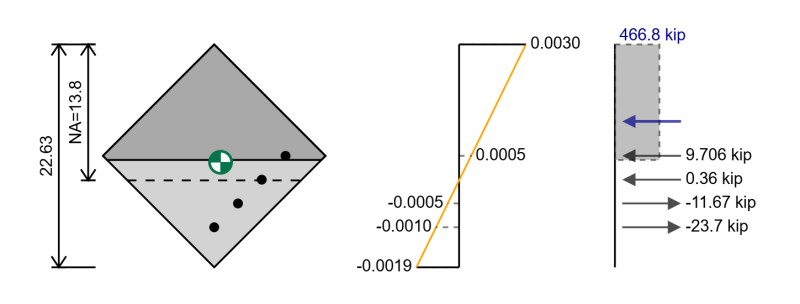
Wir können die gleichen Schritte wie für das Interaktionsdiagramm ausführen, außer jetzt werden wir unterschiedliche Positionen für unsere Verstärkung haben, und im Falle eines rechteckigen Abschnitts in biaxialer Biegung haben wir einen dreieckigen Bereich, der sich in Kompression befindet.
Anstatt die Betonkompressionskraft als zu berechnen:
Fc = 0.85 * Die Scherfestigkeit entspricht einer kombinierten Schertragfähigkeit des Betons und der Stahlbewehrung * B1 * c
Wir können stattdessen die Betonkompressionskraft als berechnen:
Fc = 0.85 * Die Scherfestigkeit entspricht einer kombinierten Schertragfähigkeit des Betons und der Stahlbewehrung * Ein
wobei a der Bereich in Kompression über der Position a = β1 ist * c
Was ist ein 3D -Interaktionsdiagramm?
Eine der Einschränkungen bei der Erstellung eines 2D -Interaktionsdiagramms für die biaxiale Biegung ist, dass es nur für eine bestimmte resultierende Momentrichtung relevant ist. Wir haben jetzt drei Variablen, um unsere Kapazität zu berücksichtigen, warum MZ sind, Mein und n. Natürlich können wir, anstatt ein 2D -Diagramm zu verwenden, das nur zwei Achsen und damit zwei Variablen verarbeiten kann.
Wie das 2D -Interaktionsdiagramm ist es unser Ziel, unsere Ladungskombinationen im Bereich der Tabelle zu haben. Der Unterschied ist nun, dass wir drei Punkte zu berücksichtigen haben (Mz, Meine,N.) und unser Punkt muss in unserem Interaktionsdiagrammvolumen enthalten sein (eher als Gebiet). Dies ist ein nützliches visuelles Instrument zur gleichzeitigen Bewertung mehrerer Punkte, aber seine Einschränkung ist, dass es schwierig ist, in 2D. Der Skyciv Section -Builder kann dazu beitragen, 3D -Interaktionsdiagramme zu erzeugen, mit denen einfach zu arbeiten ist.
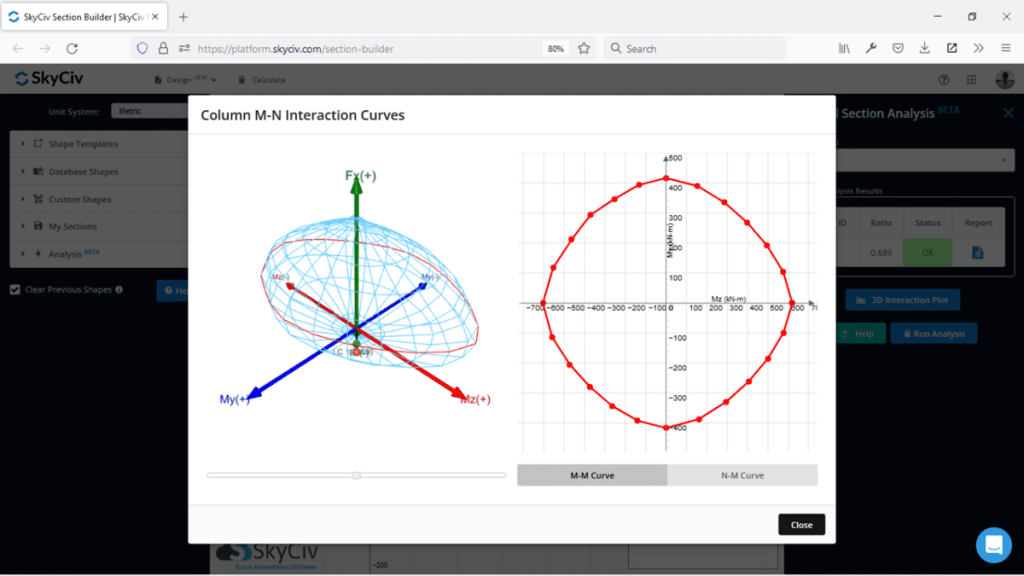
So erstellen Sie ein 3D -Interaktionsdiagramm
Um alle Datenpunkte zu erhalten, müssen wir ein 3D -Interaktionsdiagramm erstellen. Wir können die Rotation verwenden, die wir mögen, Ein vernünftiger Winkel könnte sein 15 Abschlüsse, die uns geben würden 24 Verschiedene Winkel.
Das Erhalten der Daten von Hand ist mühsam, aber möglich, aber diese Daten verwenden, um ein 3D -Interaktiven -Interaktionsdiagramm zu erstellen, ist äußerst schwierig. 3D Interaktionsdiagramme werden am besten mit Software wie Skyciv Section Builder verwendet.
Verwandte Tools
Über SkyCiv
SkyCiv bietet eine breite Palette an Cloud-Strukturanalyse- und Entwurfssoftware für Ingenieure. Als ein sich ständig weiterentwickelndes Technologieunternehmen sind wir bestrebt, bestehende Arbeitsabläufe zu erneuern und zu hinterfragen, um Ingenieuren bei ihren Arbeitsprozessen und Entwürfen Zeit zu sparen.