無料慣性モーメントと重心計算機
慣性モーメントを計算する, 重心, およびさまざまな形状の断面係数
慣性モーメント計算機の総合ガイド
SkyCiv慣性モーメントと重心電卓は、慣性モーメントを決定するのに役立ちます, 重心, および長方形を含むさまざまな形状のその他の重要な幾何学的特性, サークル, 中空部, 三角形, Iビーム, Tビーム, 角度とチャンネル. 慣性モーメントの計算方法については、以下の記事もご覧ください。, 重心と断面係数に関する詳細情報.
無料のアカウントにサインアップする前に、最大3つのセクションを解くことができます - また、より多くのソフトウェアと結果にアクセスできます. 私たちの有料アカウントは、ツールがどのようにしてこの結果に到達したかの完全な手計算を表示します. このトピックの詳細については、電卓の下を参照してください, SkyCivが提供できる他の便利なツールや機能へのリンク.
慣性電卓のSkyCivモーメントを使用する方法
以下のビデオデモを見て、電卓を使い始めましょう.
評価したい断面形状をドロップダウンリストから選択するだけ, 選択したセクションの寸法を入力し、[計算] をクリックします.
この無料の多目的計算機は、当社のフルスイート構造解析ソフトウェアから取得されました. それはすることができます:
- 慣性モーメントを計算する (私) ビーム断面の (面積の2番目の瞬間)
- 重心を計算する (C) ビーム断面のX軸とY軸
- 面積の最初の瞬間を計算する (静的慣性モーメント) (Q) ビーム断面の
- 断面係数を計算するための断面係数計算機 (と) ビーム断面の
- ねじり定数を計算する (J) ビーム断面の
共通セクション プロパティの定義
慣性モーメント計算機は、構造工学で使用されるいくつかの重要な断面特性を正確に計算します. セクション プロパティの用語と定義の簡潔なリストを次に示します。:
- セクションの面積 (あ) – 断面積は非常に単純な計算です, ただし、軸応力計算で直接使用されます (より多くの断面積, より軸方向の強度)
- 慣性モーメント (から, いや) – 面積の二次モーメントとも呼ばれます, は、部材の強度とたわみに対する抵抗を決定するために使用される計算です. この数が多いほど, セクションが強い. ここには2つの軸があります:
- 長軸 (から) – これは Z 軸に関するもので、通常は部材の最も強い方向であるため、通常は主軸とみなされます。
- マイナー 軸 (いや) – これは Y 軸に関するもので、短軸または弱軸と見なされます。. これは、セクションがこの軸の周りにそれほど力を加えるように設計されていないためです。
- 形状が両方向で同じ寸法である場合も注意する価値があります (平方, 円形など。) これらの値は両方向で同じになります. 詳細については、円の慣性モーメントを参照してください.
- 重心 (Cz, Cy) – これはセクションの重心であり、通常は Z 成分と Y 成分を持ちます。. 対称形状の場合, これは幾何学的中心になります. 非対称形状の場合 (角度など, チャネル) これらは異なる場所にあります. ビーム断面の重心を計算する方法を学ぶ. 上記の計算機は、あらゆる種類の形状の X および Y 重心を計算することもできます。.
- 静的慣性モーメント (Qz, Qy) – エリアの最初の瞬間とも呼ばれます, これは、軸からのビームセクションの面積の分布を測定します. 慣性モーメントのように, これらはZ方向とY方向の両方にあります. これらは通常、せん断応力の計算に使用されます, したがって、この値が大きいほど、断面はせん断に対して強くなります。. 計算機はこの値を提供します, 断面一次モーメントの計算の詳細については、ここをクリックしてください.
- 弾性断面係数 (Sz, アメリカのサイ. グーグー, 英国またはオーストラリアの Zy) – 静的断面係数とも呼ばれます, 曲げ応力の計算に使用されます. それらは通常、上部と下部の繊維セクションに対して計算されます. 例えば, Szt は、断面の上部繊維までの Z 軸周りの断面弾性率です。.
- ねじり定数 (J) – 極慣性モーメントまたは J とも呼ばれます。, ねじれまたはねじり変形に対する材料の抵抗を表す値です。.
- 塑性断面係数 (S) – 塑性曲げに抵抗する断面形状の能力の測定, 材料が降伏し始めるときの応力を推定するために使用されます (塑性限界に達する) 特定の荷重下で、通常、荷重下のビームの設計と解析に使用されます.
その他のパラメータ – これらは、完全な SkyCiv Section Builder によって計算されたより高度な結果です:
- 慣性の積 (Z軸とY軸について): 特定の軸を中心とした回転に対する形状の抵抗の尺度, 軸から形状上の任意の点までの距離と、点の慣性モーメントの対応する成分の外積に等しい.
- プラスチック断面係数 (Z軸とY軸について): 塑性曲げに抵抗する断面形状の能力の尺度, 材料が降伏し始めるときの応力を推定するために使用されます (塑性限界に達する) 特定の負荷の下で.
- プラスチック中性軸 (Z軸とY軸について): 塑性変形をもたらすために、形状に作用するすべての力が通過しなければならない断面形状の軸。.
- せん断領域 (Z軸とY軸について): せん断力に抵抗するのに有効な断面形状の面積.
- せん断中心から図心までの距離 (Z軸とY軸の両方で): SkyCiv重心計算機は、せん断中心と断面形状の重心との間の距離を計算するのに役立ちます.
- ねじり定数 (FEAの使用): ねじれまたはねじり変形に対する材料の抵抗を表す値, 有限要素解析を使用して計算.
- ねじり半径: 実際の形状と同じねじれ定数になるように、断面形状の領域が集中しなければならない軸からの距離.
- 反り定数: 反りやゆがみ変形に対する材料の耐性を表す値.
- 単対称定数 (Z軸とY軸について): 断面形状が特定の軸に対してどの程度対称であるかの尺度, 完全な対称性を示すゼロの値.
- 回転半径 (Z軸とY軸について): 実際の形状と同じ慣性モーメントになるように、断面形状の面積を集中させる必要がある軸からの距離.
- 主軸の回転角: 断面形状の中立軸と主軸の間の角度.
慣性モーメントについて, 図心およびその他のセクション プロパティ
また、セクションの慣性モーメントを計算するための詳細情報もまとめました。. この完全なガイドは、慣性モーメントに関連するすべての事柄に関する包括的な知識ベースを提供するのに役立ちます, 重心, 断面係数およびその他の重要な幾何断面特性. 以下のセグメントで, 慣性モーメントとは何かを含めます, 重心の計算方法, SkyCiv Moment of Inertia and Centroid Calculatorの助けを借りた慣性モーメントと一般的なMOI方程式.
慣性モーメントとは?
慣性モーメント (より技術的には、面積の慣性モーメントとして知られています, または面積の二次モーメント) は、構造工学で使用される重要な幾何学的特性です。. それはあなたのセクションが持っている材料強度の量に直接関係しています.
一般的に言えば, 詳細な内訳, セクションの強度が高いほど, その結果、荷重下でのたわみが少なくなります. 長方形の慣性モーメント, 詳細な内訳, 技術的には、軸の周りの質量を加速するために必要なトルクの量の測定値です - したがって、慣性という言葉はその名前に含まれています.
慣性モーメントの求め方 - 長方形
長方形の慣性モーメントを計算するには, 式を使用できます:
私= (b * h^3) / 12
I は長方形の慣性モーメント
b は長方形の幅です
h は長方形の高さです
b と h の測定単位が一致している必要があることに注意することが重要です。 (例えば, インチ, ミリメートル, 等). また、最終結果の単位は入力単位に依存します, たとえば、入力がメートル単位の場合、結果の単位は m^4 になります。.
慣性モーメントの計算例
次の寸法の長方形があるとしましょう:
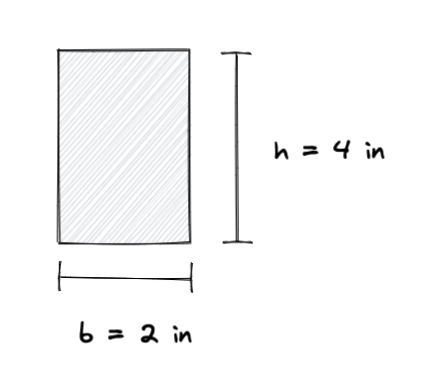
慣性モーメントの計算式の使用, 長方形の慣性モーメントは次のように計算できます。:
私= (b * h^3) / 12
私= (2 * 4他のいくつかの例は) / 12
私= (2 * 64) / 12
= 10.67 ^4
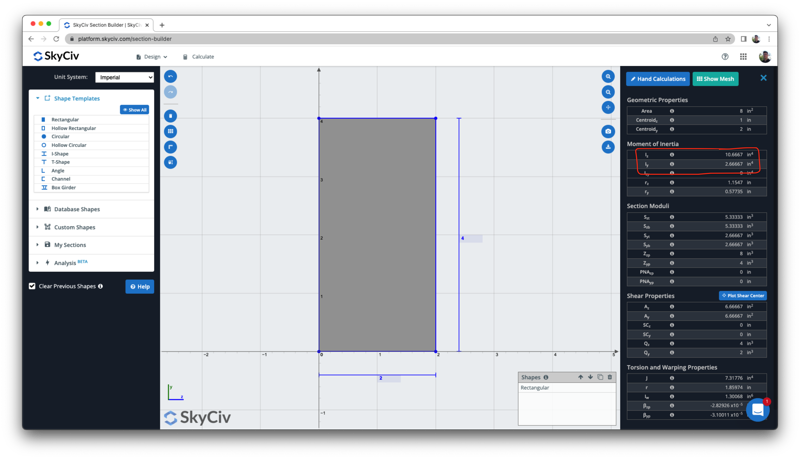
したがって、長方形の慣性モーメントは 10.67 インチ^4. この慣性モーメントは重心軸周りです, 別の軸について慣性モーメントを求める必要がある場合は、, 別の式を使用するか、変換を実行する必要があります. また、単位が常に入力単位の電力の積であることも確認できます, この場合、すべての入力単位はインチです, したがって、結果はインチ^ 4になります.
この結果は、上記の自由慣性モーメント計算機で確認できます。, の同じ結果を示します 10.6667 ^4:
慣性モーメントの求め方 - アイビーム
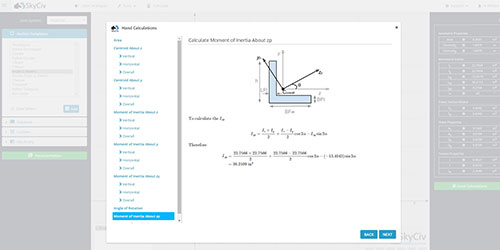
次に、断面が I ビームである、より複雑なケースを見てみましょう。, 異なるフランジ寸法. コンセプトは同じ, ただし、この場合のアプローチはまったく異なります. 基本的に, Iビームをさまざまな長方形の組み合わせとして見て、さまざまな部分を合計して、セクション全体の慣性モーメントを取得する必要があります. 要するに, この3つのステップに従う必要があります:
- セクション全体の中立軸を計算する
- 各パーツのMOIを計算する
- 平行軸の定理を使用して慣性モーメントを計算する - これは本質的に個々の慣性モーメントの合計です
それでは、次のセクションを考えてみましょう:
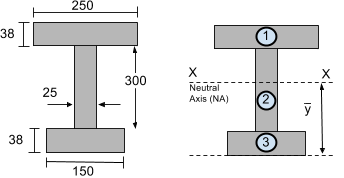
中立軸 (NA) 重心にあります. これは基本的に、各セグメントの面積と底からの距離の加重平均です. 垂直方向を計算するために重心方程式を使用するだけです。 (そして) マルチセグメント形状の図心.

ビーム セクションの下部から基準線または基準線を取得します。. 次に、上に示した I ビーム セクションの各セグメントの Ai と yi を見つけて、垂直方向または y 重心を見つけることができるようにします。.


これで重心が得られました. 引き続き慣性モーメントを計算できます. セクションの総慣性モーメントを計算するには、 "平行軸定理" 以下に定義されているように:

3つの長方形のパーツに分割したので, これらの各セクションの慣性モーメントを計算する必要があります. 簡略化された直角慣性モーメントの式を使用できるようになりました:
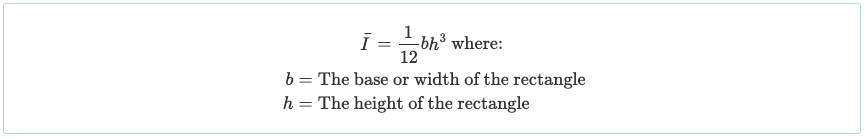
これで、使用する必要があるすべての情報が揃いました。 "平行軸定理" Iビーム断面の総慣性モーメントを求めます. 慣性モーメントの例:

もう一度, この結果を自由モーメント慣性計算機の結果と比較して、重心と慣性モーメントの両方の結果を比較できます。, ここで、両方の重心 (216.29 に) と慣性モーメント (4.74 x 10^8 インチ^4) マッチ:
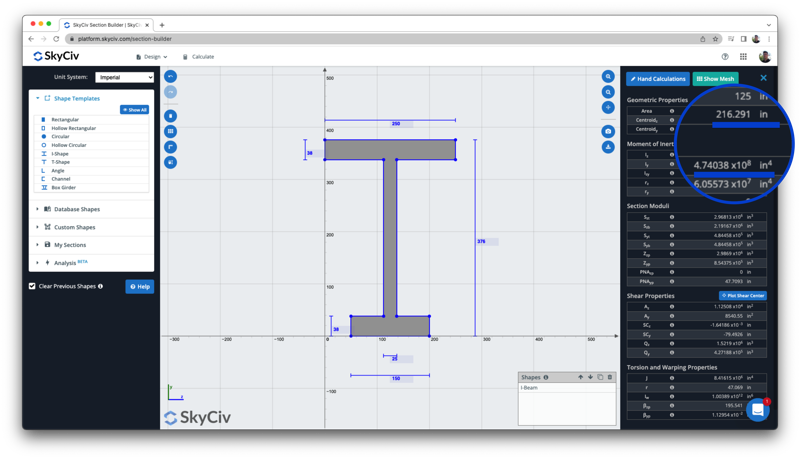
詳細については, のチュートリアルにアクセスしてください ビーム断面の慣性モーメントの計算.
慣性モーメントの式
単純な式を使用して、一般的な形状や断面の慣性モーメントを計算することもできます. これらは、迅速な値を提供する慣性モーメント方程式であり、結果を相互参照または再確認するための優れた方法です。. シンプルな形だけにこだわる, 以下の図は、これらの方程式の一部を示しています:
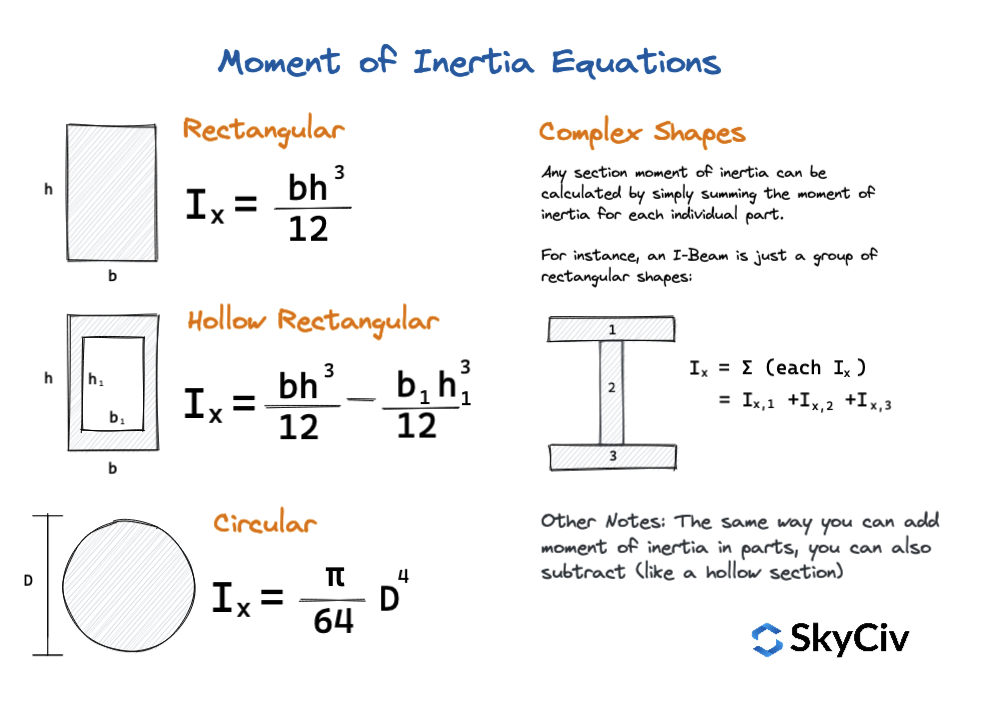
SkyCiv重心電卓
重心, 「幾何学的な中心」としても知られています, 均一な密度を持つ物体の質量の中心です. 重心の簡略化されたデモンストレーション, 指の上でバランスを取るために鉛筆を置く必要がある位置です。. 鉛筆のバランスが取れて指から落ちない位置が、鉛筆の重心のおおよその位置になります。. 材料の質量と密度を考慮して、指の両側で鉛筆の質量が等しい点を決定します。, したがって、鉛筆の「重心」を表します.
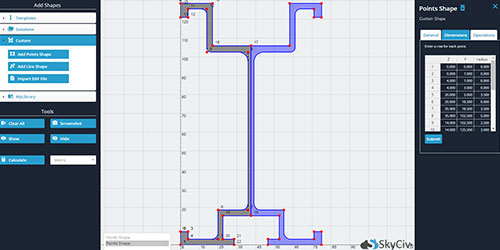
SkyCiv Centroid Calculator は FEA を使用して、数秒で高精度の結果を提供します。, どんなに複雑な形でも. プレミアム版では, ユーザーは形状を定義する点の座標を入力でき、計算機は重心の座標を提供します. これには、DXF インポートを介してカスタム形状をデザインする機能が含まれます。, 多数 (構築された) シェイプとカスタムポイントシェイプ.
そのスピードと正確さに加えて, 私たちの重心計算機も信じられないほど使いやすいです. シンプルなユーザーインターフェースで, セクションの寸法を入力し、セクションのプロパティ値を受け取ることができます (ビーム断面図心を含む) 数秒以内に. デザインプロジェクトに取り組んでいるかどうか, さまざまなセクションを試したり、試験の勉強をしたりする, SkyCiv Centroid Calculator は、仕事を完了するのに役立つ完璧なツールです。.
断面係数計算機
前述のとおり, この無料ツールは、弾性断面係数の計算も提供します, ただし、エンジニアとして始めたばかりの場合は、セクション モジュラスが何であるかを理解していない可能性があります。. 簡単に言えば, 断面係数は、曲げに対する抵抗を測定する断面の断面特性であり、中立軸から最も遠いファイバーまでの距離に対する慣性モーメントの比として計算されます。. 弾性断面係数は、この式で単純に次のように表されます。:
どこ,
- S は断面係数です
- I は中立軸を中心とした断面の慣性モーメントです。
- y は中立軸からセクションの最も遠い点までの距離です。
断面係数には 2 種類あります: 弾性とプラスチック. アメリカでは, S は通常、弾性断面係数を表すために使用され、Z は塑性断面係数を表すために使用されます。. イギリスとオーストラリアでは, これらは通常逆になります. 弾性断面係数は通常、文字 Z で表されます, 塑性断面係数は文字 S で参照されます。.
一般に, 弾性断面係数は、ほとんどの金属の降伏点まで適用できるため、断面設計に使用されます。. 金属は通常、材料の降伏点を超えるように設計されていません.
追加ドキュメント
慣性モーメントの詳細については、次のドキュメント ページを参照してください。, さまざまな形状についてそれらを計算する方法, 重心計算機の使い方:
より多くの無料ツールが利用可能
SkyCivは、Iビームサイズツールや無料の構造設計ソフトウェアなどの他のツールも提供しています. 動的セクションドロワーには、ビームセクションのグラフィック表示も表示されます. したがって、円の慣性モーメントを計算する場合, 長方形またはその他の形状の慣性モーメント, 以下のソフトウェアまたは当社のオールインクルーシブのSkyCiv Section Builderを自由に使用してください.
SkyCivは、エンジニアに幅広いCloud Structural Analysis and Design Softwareを提供しています. 常に進化するテクノロジー企業として, 私たちは、既存のワークフローの革新と挑戦に取り組み、エンジニアの作業プロセスと設計の時間を節約します.
より多くの機能が必要?
にアップグレード プロの計画 完全な機能のロックを解除する