Έχετε αναρωτηθεί ποτέ πώς λειτουργεί ουσιαστικά το δομικό λογισμικό? Απλώς συνέχισε να διαβάζεις, και θα βρείτε πώς μπορούμε να χρησιμοποιήσουμε την πλατφόρμα SkyCiv και τον προγραμματισμό Python μέσα από ένα παράδειγμα που αναπτύχθηκε σε μια τάξη Δομικής Ανάλυσης.
Μια γρήγορη ανασκόπηση της δομικής ανάλυσης
Συχνά χρησιμοποιούμε διαθέσιμο λογισμικό για την επίλυση μιας δομικής ανάλυσης, που έχει ως αποτέλεσμα δυνάμεις, μετατόπιση, στρες, και τα λοιπά. Με απλά λόγια, το πρόβλημα πέφτει στην παρακάτω μορφή:φά=κ∙ρε
F=K∙ρε
Οπου:
- F είναι οι διανυσματικές δυνάμεις
- K είναι η ακαμψία της δομής
- d είναι το πεδίο μετατόπισης
Ο κύριος στόχος είναι η μετατροπή μιας συνεχούς δομής σε διακριτή “κομμάτια” ενός συγκροτήματος και να το αναλύσετε, λήψη δυνάμεων και μετατοπίσεων. Πρέπει να ακολουθηθεί ένας γενικός δρόμος:
- Προεπεξεργασία: το πρώτο βήμα στη δομική ανάλυση, όπου παίρνουμε τα δεδομένα δομής, γεωμετρία, ιδιότητες υλικού, και φορτώνει και οριστικοποιεί όταν η καθολική μήτρα ακαμψίας κατασκευάζεται.
- Επεξεργάζομαι, διαδικασία: όπου λύνουμε την προηγούμενη έκφραση, φά=κ∙ρε F=K∙ρε. Μερικές μέθοδοι γενικά αποδεκτές για την επίλυση του συστήματος γραμμικών εξισώσεων είναι το Gauss-Jordan, Gaussian εξάλειψη, και τα λοιπά.
- Μεταδιεργασία: το τελευταίο μέρος για να εμφανιστούν τα αποτελέσματα όσον αφορά τις δυνάμεις και την πίεση, αν είναι απαραίτητο.
Παράδειγμα επίπεδου πλαισίου
Το παράδειγμα περίπτωσης αποτελείται από ένα κανονικό επίπεδο πλαίσιο (Φιγούρα 1).
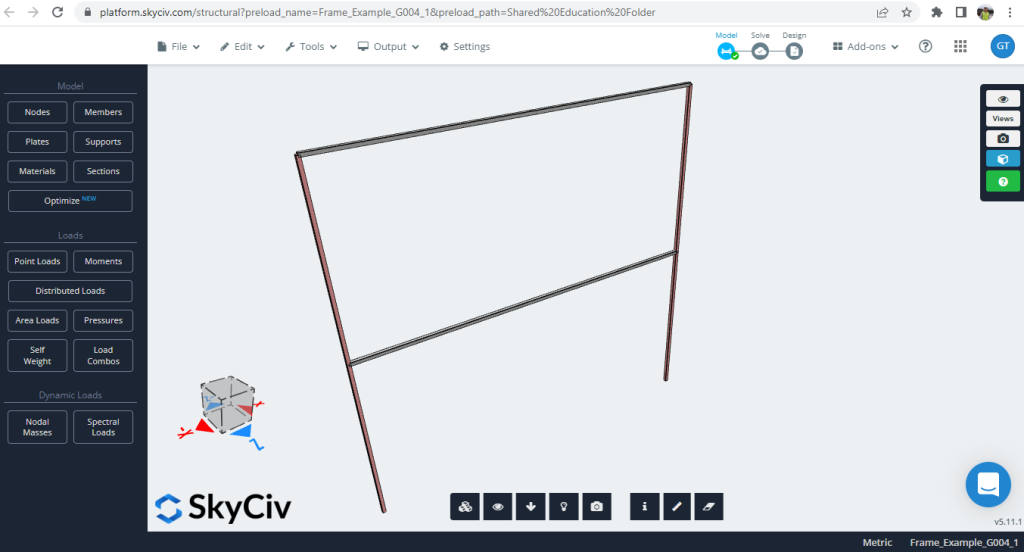
Φιγούρα 1. Παράδειγμα δομικού 2D πλαισίου
Ιδιότητες του στοιχείου για στήλες, δοκάρια, και υλικά είναι:
| Δομικό στοιχείο | Περιοχή, (mm^2) | Αδράνεια, (mm^4) |
|---|---|---|
| Στήλες | 93,000 | 720,000,000 |
| δοκοί | 140,000 | 2,430,000,000 |
Ιδιότητες σκυροδέματος:
- Αντοχή υλικού, φά′ντο=20ΜΠένα f′c=20MPa
- Το μέτρο του Young, μι=17000ΜΠένα E=17000MPa
Προγραμματισμός Python και μοντελοποίηση SkyCiv
Τώρα είναι η ώρα να ξεκινήσετε να εργάζεστε παράλληλα με το modeling σε Python και SkyCiv. Φιγούρα 2 δείχνει τα δεδομένα εισόδου (κόμβοι, στοιχεία, βαθμοί ελευθερίας, τοπικός προσανατολισμός άξονα) για τον κώδικα που αναπτύχθηκε στην Python. Μπορείτε να ελέγξετε μόνοι σας το αρχείο και να εκτελέσετε το παράδειγμα μέσω αυτού Σύνδεσμος.
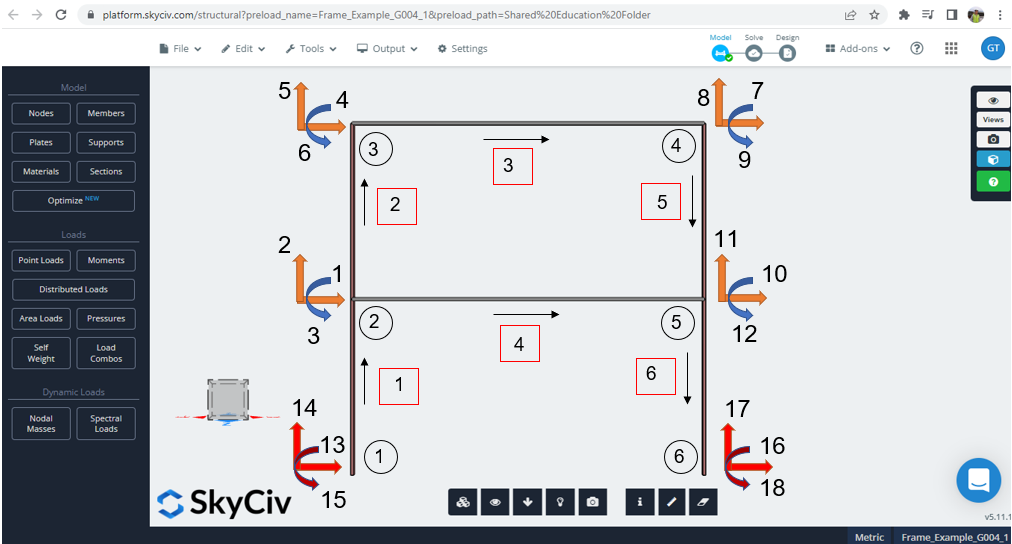
Φιγούρα 2. Συνάρτηση τοπικής μήτρας ακαμψίας
Το αρχείο Python χρησιμοποιεί ένα παράδειγμα λειτουργικού προγραμματισμού επειδή είναι εύκολο να εξηγηθεί και να αναπτυχθεί στην τάξη. Αυτό συνίσταται στη διαίρεση και την κατάκτηση, διαμορφώνοντας την κατασκευή του κώδικα και τις μεθόδους του.
Κατά την κωδικοποίηση της μεθόδου, Το πιο σημαντικό είναι να ορίσετε τη μαθηματική διατύπωση που θα εφαρμοστεί. Θα χρησιμοποιήσουμε τη δοκό Euler Bernoulli:
Οι διαφορές στις αξίες (Python Script και SkyCiv S3D) είναι ήσσονος σημασίας, με περίπου 2.90% ως το μέσο.
2. Αξονικές δυνάμεις
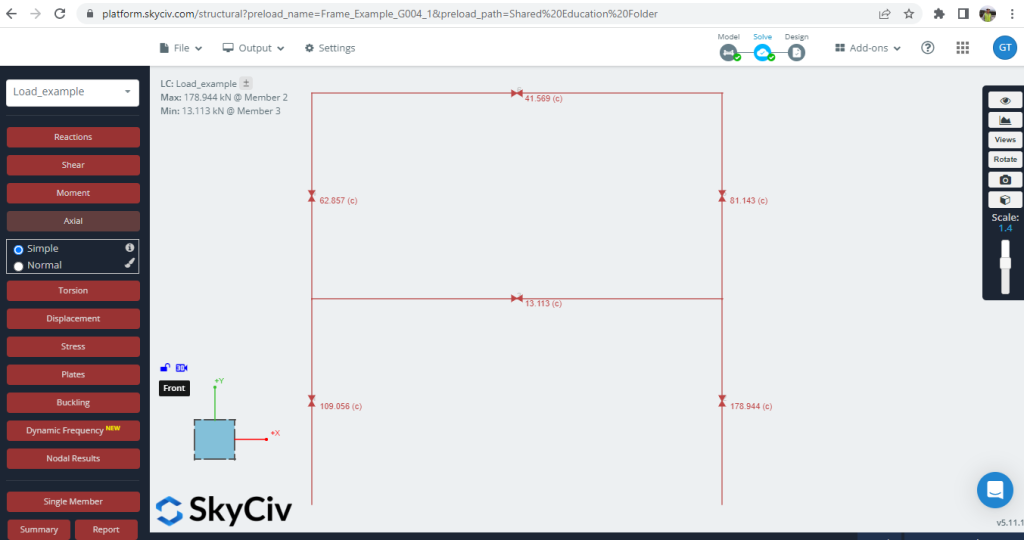
Φιγούρα 5. Αξονικές δυνάμεις αναπτύχθηκαν στο πλαίσιο
| Ερ, ΚΝ, SkyCiv | Ερ, ΚΝ, Σενάριο Python | (Δέλτα )% |
|---|---|---|
| 109.056 | 109.519 | 0.423 |
| 62.857 | 62.616 | 0.383 |
| 41.589 | 43.252 | 3.845 |
| 13.113 | 11.709 | 10.707 |
| 81.143 | 81.384 | 0.296 |
| 178.944 | 178.480 | 0.2593 |
Οι διαφορές στις αξίες (Python Script και SkyCiv S3D) είναι ήσσονος σημασίας, με περίπου 2.65 % ως το μέσο.
3. Διατμητικές δυνάμεις
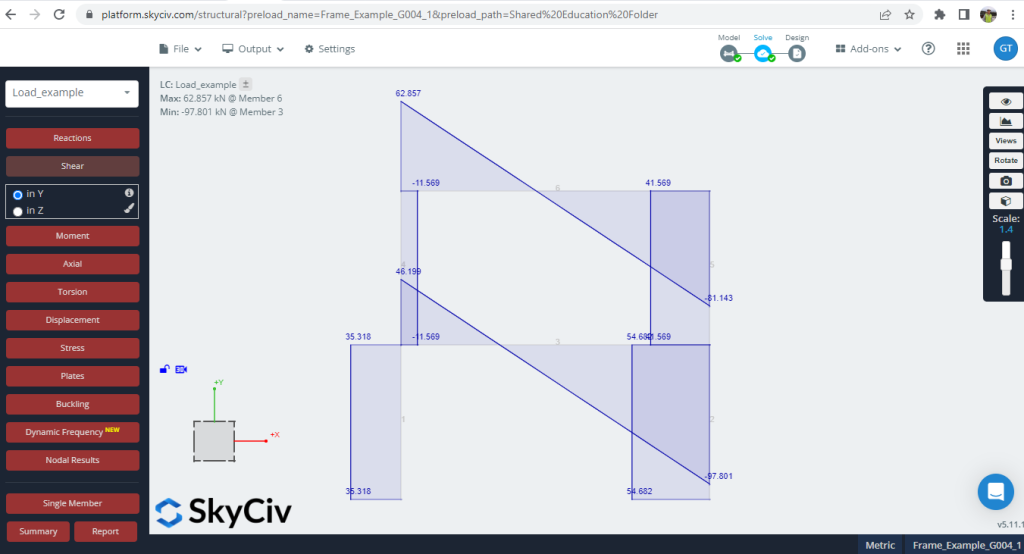
Φιγούρα 6. Οι δυνάμεις διάτμησης αναπτύχθηκαν στο πλαίσιο
| Ερ, ΚΝ, SkyCiv | Ερ, ΚΝ, Σενάριο Python | (Δέλτα )% |
|---|---|---|
| 35.318 | 35.039 | 0.790 |
| 35.318 | 35.039 | 0.790 |
| -11.569 | 13.252 | 12.700 |
| -11.569 | 13.252 | 12.700 |
| 62.857 | 62.616 | 0.383 |
| -81.143 | -81.384 | 0.296 |
| 46.199 | 46.903 | 1.501 |
| -97.801 | -97.097 | 0.720 |
| 41.569 | 43.252 | 3.891 |
| 41.569 | 43.252 | 3.891 |
| 54.682 | 54.961 | 0.508 |
| 54.682 | 54.961 | 0.508 |
Οι διαφορές στις αξίες (Python Script και SkyCiv S3D) είναι ήσσονος σημασίας, με περίπου 3.22% ως το μέσο.
4. Στιγμές κάμψης
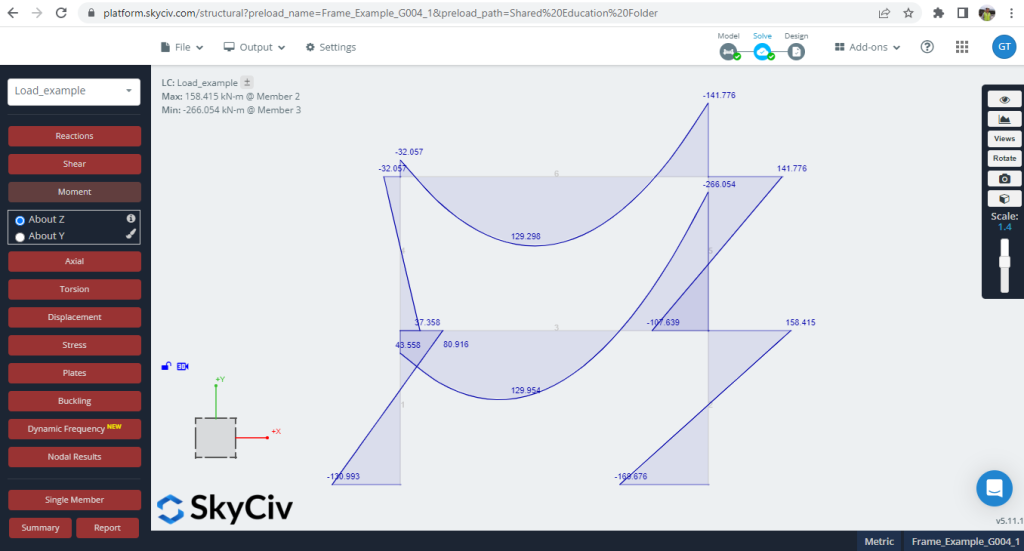
Φιγούρα 7. Στιγμές αναπτύχθηκαν στο κάδρο
| Ερ, kN-m, SkyCiv | Ερ, kN-m, Σενάριο Python | (Δέλτα )% |
|---|---|---|
| -130.993 | -133.213 | 1.667 |
| 80.916 | 77.022 | 4.812 |
| 37.358 | 42.713 | 12.537 |
| -32.057 | -36.797 | 12.881 |
| -32.057 | -36.797 | 12.881 |
| -141.776 | -149.400 | 5.103 |
| 43.558 | 34.309 | 21.234 |
| -266.054 | -266.859 | 0.302 |
| 107.639 | 110.109 | 2.243 |
| -141.776 | -149.400 | 5.103 |
| 169.676 | 173.016 | 1.930 |
| -158.415 | -156.749 | 1.052 |
Οι διαφορές στις αξίες (Python Script και SkyCiv S3D) είναι ήσσονος σημασίας, με περίπου 6.81% ως το μέσο.
5. συμπέρασμα
Αυτή η ανάρτηση έχει χρησιμεύσει ως δοκιμή ότι το πλατφόρμα SkyCiv είναι ένας εξαιρετικός πόρος για εκπαιδευτικούς σκοπούς λόγω των ισχυρών του δυνατοτήτων στη δομική ανάλυση. Χρήση προγραμματισμού Python και σύγκριση των αποτελεσμάτων με ακριβές λογισμικό όπως το SkyCiv, είναι απαραίτητο που κάθε μάθημα μηχανικής πρέπει να περιλαμβάνει στο βασικό του περιεχόμενο.


