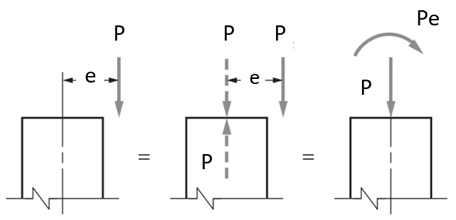
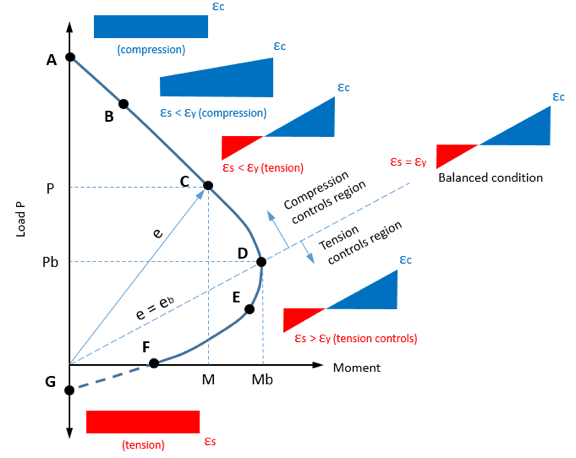
 Voorbeeld van een interactiecurve
Voorbeeld van een interactiecurve- Pure axiale compressie (punt A). Dit is de grootste axiale compressiebelasting die de kolom kan dragen.
- Compressie met kleine buiging (punt B). Dit is het geval van een grote axiale belasting die werkt bij een kleine excentriciteit. De spanningsverdeling wordt schuin, maar de sectie staat nog steeds onder druk. Falen treedt op door het breken van het beton.
- Compressie controle (punt C). Hier bestaan zowel compressiezone als trekzone van beton. Staal staat onder spanning. Bezwijken ontstaat door het verbrijzelen van het beton aan de drukzijde, terwijl de spanning in staal fs kleiner is dan de vloeigrens fy.
- Evenwichtige conditie (punt D). Een evenwichtige toestand wordt bereikt wanneer de drukspanning in het beton beperkt wordt en de trekwapening gelijktijdig meegeeft. Bezwijken van beton vindt plaats op hetzelfde moment als het staal vloeit.
- Spanningscontrole: (punt E). Dit is het geval bij een kleine axiale belasting met grote excentriciteit, dat is, een groot moment. Bij een mislukking, de rek in het spanstaal is groter dan de rekgrens.
- Pure buiging flex (punt F). De sectie wordt in dit geval onderworpen aan een buigend moment M, terwijl de axiale belasting P = . is 0. Falen treedt op als in een balk die alleen aan een buigmoment wordt onderworpen.
- Pure axiale spanning (punt G). Dit is de grootste axiale trekbelasting die een kolom kan dragen.
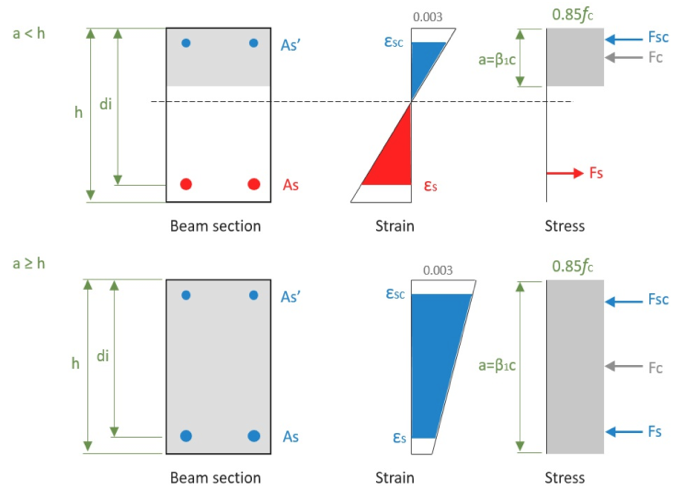
- Spanningen in beton en staal zijn evenredig met de afstand tot de neutrale as
- Aan evenwicht van krachten en spanningscompatibiliteit moet worden voldaan
- De maximaal bruikbare drukspanning in beton is 0.003
- Sterkte van beton onder spanning kan worden verwaarloosd
- Het betonnen spanningsblok kan worden genomen als een rechthoekige vorm

Interactiecurve interpreteren
Om het ontwerp van een kolom als adequaat te beschouwen (veilig), de combinatie van actie-effecten (M, P.) moet kleiner zijn dan de combinatie van ontwerpsterkten (M, P.) uit de interactiecurve. Dit betekent dat als de positie van de M,P-punt op het perceel ligt buiten de curve en wordt geacht niet aan deze criteria te voldoen en wordt als onveilig beschouwd.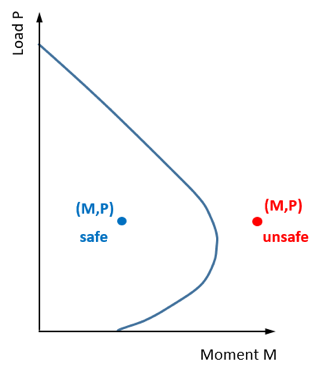
SkyCiv gewapend beton ontwerp
SkyCiv biedt een volledig uitgeruste Ontwerp van gewapend beton software waarmee u betonnen balk- en betonkolomontwerpen kunt controleren volgens ACI 318, ALS 3600 en EN2 Ontwerpnormen. De software is gebruiksvriendelijk en volledig cloudgebaseerd; vereist geen installatie of downloaden om te beginnen!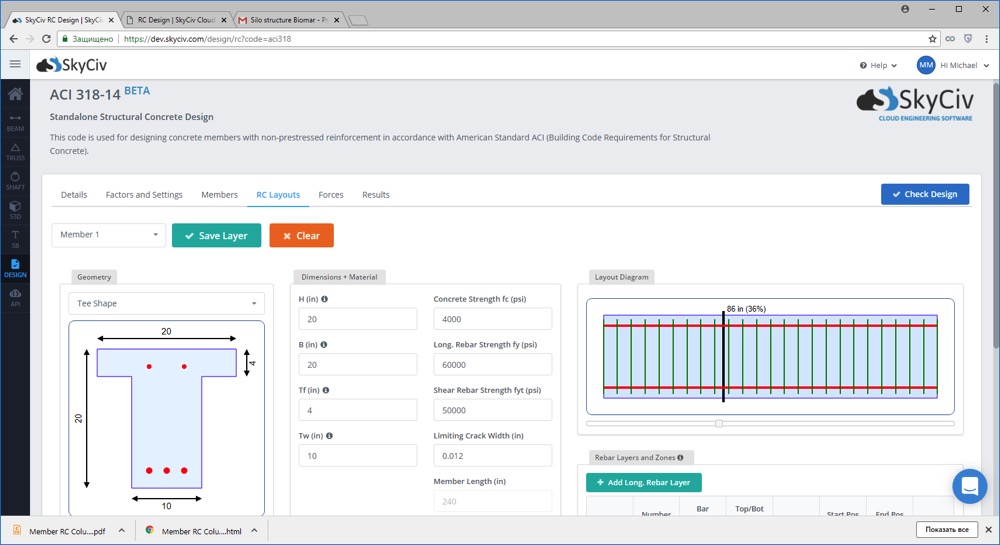
Michael Malgin
Bouwkundig ingenieur, Product ontwikkeling
MEng (Civiel)
[email protected]
Bouwkundig ingenieur, Product ontwikkeling
MEng (Civiel)
[email protected]



