Gratis traagheidsmoment en zwaartepunt calculator
Bereken het traagheidsmoment, Zwaartepunt, en sectiemodulus voor een breed scala aan vormen
Een uitgebreide handleiding voor onze Traagheidsmoment Calculator
SkyCiv Traagheidsmoment en Zwaartepunt Calculator helpt je het traagheidsmoment, zwaartepunt, en andere belangrijke geometrische eigenschappen te bepalen voor verschillende vormen, waaronder rechthoeken, cirkels, holle secties, driehoeken, I-profielen, T-profielen, hoeken en kanalen. We hebben ook enkele artikelen hieronder over hoe je het traagheidsmoment kunt berekenen, evenals meer informatie over zwaartepunten en sectiemodulus.
Je kunt tot drie secties berekenen voordat je je moet aanmelden voor een gratis account - waarmee je ook toegang krijgt tot meer software en resultaten. Ons betaalde account toont de volledige handberekeningen van hoe de tool tot dit resultaat is gekomen. Raadpleeg hieronder de calculator voor meer informatie over dit onderwerp, evenals links naar andere nuttige tools en functies die SkyCiv je kan bieden.
Hoe gebruik je de SkyCiv Traagheidsmoment Calculator
Bekijk de video-demonstratie hieronder om aan de slag te gaan met onze calculator.
Kies simpelweg de doorsnede vorm die je wilt evalueren uit de keuzelijst, voer de afmetingen van je gekozen sectie in en klik op Bereken.
Deze gratis multifunctionele calculator is afkomstig uit onze volledige suite Structural Analysis Software. Hiermee kun je:
- Het traagheidsmoment (I) van een balksectie berekenen (Tweede Oppervlaktemoment)
- Bereken het zwaartepunt (C) in de X- en Y-as van een balksectie te berekenen
- Het eerste oppervlakte moment (Statistisch Traagheidsmoment) (Q) van een balksectie berekenen
- Een sectiemodulus calculator om de sectiemodulus (Z) van een balksectie berekenen
- De torsieconstante (J) van een balksectie berekenen
Veelgebruikte sectie-eigenschappen definities
De traagheidsmoment calculator zal nauwkeurig een aantal belangrijke sectie-eigenschappen berekenen die in de bouwkunde worden gebruikt. Hier is een beknopte lijst van de sectie-eigenschappen termen en definities:
- Oppervlakte van de sectie (A) - De sectieoppervlakte is een vrij eenvoudige berekening, maar wordt direct gebruikt in berekeningen van axiale spanning (hoe groter de doorsnede oppervlakte, hoe meer axiale sterkte)
- Traagheidsmoment (Van, Iy) - ook bekend als tweede oppervlakte moment, is een berekening die wordt gebruikt om de sterkte van een element en zijn weerstand tegen doorbuiging te bepalen. Hoe hoger dit getal, hoe sterker de sectie. Er zijn hier twee assen:
- Hoofd-as (Van) – Dit is rond de Z-as en wordt meestal beschouwd als de hoofd-as omdat dit meestal de sterkste richting van het element is
- Neven as (Iy) - Dit is rond de Y-as en wordt beschouwd als de neven- of zwakke as. Dit komt omdat secties niet zijn ontworpen om zoveel kracht over deze as te weerstaan
- Het is ook de moeite waard op te merken dat als een vorm dezelfde afmetingen in beide richtingen heeft (vierkant, cirkel, enz.) deze waarden in beide richtingen hetzelfde zullen zijn. Zie Traagheidsmoment van een cirkel om meer te leren.
- Zwaartepunt (Cz, Cy) - dit is het zwaartepunt van de sectie en heeft meestal een Z- en Y-component. Voor symmetrische vormen, zal dit het geometrische middelpunt zijn. Voor niet-symmetrische vormen (zoals hoek, Kanaal) zullen deze op verschillende locaties zijn. Leer hoe je het zwaartepunt van een balksectie kunt berekenen. De bovenstaande rekenmachine berekent ook het X- en Y-zwaartepunt van elk type vorm.
- Statistisch Traagheidsmoment (Qz, Qy) - Ook bekend als Eerste Oppervlakte Moment, meet dit de verdeling van de oppervlakte van een balksectie vanaf een as. Net als het traagheidsmoment, zijn deze in zowel de Z- als Y-richting. Deze worden meestal gebruikt in schuifspanning berekeningen, dus hoe groter deze waarde, hoe sterker de sectie is tegen afschuiving. De calculator zal deze waarde verstrekken, maar klik hier om meer te leren over het berekenen van het eerste oppervlakte moment.
- Elastische Sectiemodulus (Sz, Sy in Amerika. Zz, Zy in Groot-Brittannië of Australië) – Ook bekend als statische sectiemodulus, en wordt gebruikt in buigspanningsberekeningen. Ze worden meestal berekend tot de bovenste en onderste vezels van de sectie. Bijvoorbeeld, Szt is de sectiemodulus over de Z-as naar de bovenste vezel van de sectie.
- Torsieconstante (J) - ook bekend als het polaire traagheidsmoment of J, is een waarde die de weerstand van een materiaal tegen verdraaiing of torsionele vervorming beschrijft.
- De Plastische Sectiemodulus (S) - een meting van het vermogen van een doorsnede vorm om plastische buiging te weerstaan, gebruikt om de spanning van een materiaal te schatten wanneer het begint te vloeien (zijn plastische limiet bereikt) onder een specifieke belasting en wordt meestal gebruikt voor het ontwerp en de analyse van balken onder belasting.
Andere Parameters – Dit zijn meer geavanceerde resultaten die worden berekend door de volledige SkyCiv Section Builder:
- Product van Traagheid (over Z- en Y-as): Een maat voor de weerstand van een vorm tegen rotatie over een specifieke as, gelijk aan het kruisproduct van de afstand van de as tot elk punt op de vorm en de bijbehorende component van het traagheidsmoment van het punt.
- Plastische Sectiemodulus (over Z- en Y-as): Een maat voor het vermogen van een doorsnede vorm om plastische buiging te weerstaan, gebruikt om de spanning van een materiaal te schatten wanneer het begint te vloeien (zijn plastische limiet bereikt) onder een specifieke belasting.
- Plastische Neutrale (over Z- en Y-as): Een as in een doorsnede vorm waar alle krachten die op de vorm werken doorheen moeten gaan om plastische vervorming te veroorzaken.
- Afschuifoppervlakte (over Z- en Y-as): De oppervlakte van een doorsnede vorm die effectief is in het weerstaan van schuifkrachten.
- Afstand van Afschuifcentrum tot Zwaartepunt (in zowel Z- als Y-as): SkyCiv zwaartepunt calculator helpt de afstand te berekenen tussen het afschuifcentrum en het zwaartepunt van een doorsnede vorm.
- Torsieconstante (met FEA): Een waarde die de weerstand van een materiaal tegen verdraaiing of torsionele vervorming beschrijft, berekend met behulp van Eindige Elementen Analyse.
- Torsiestraal: De afstand vanaf een as waarop de oppervlakte van een doorsnede vorm moet worden geconcentreerd om te resulteren in dezelfde torsieconstante als de werkelijke vorm.
- Warping Constante: Een waarde die de weerstand van een materiaal tegen vervorming of vervormingsvervorming beschrijft.
- Monosymmetrie Constante (over Z- en Y-as): Een maat voor hoe symmetrisch een doorsnede vorm is over een specifieke as, met een waarde van nul die perfecte symmetrie aangeeft.
- Stralingsradius (over Z- en Y-as): De afstand vanaf een as waarop de oppervlakte van een doorsnede vorm moet worden geconcentreerd om te resulteren in hetzelfde traagheidsmoment als de werkelijke vorm.
- Hoek van Rotatie van Hoofdas: De hoek tussen de neutrale as en hoofdas van een doorsnede vorm.
Over Traagheidsmomenten, Zwaartepunten en andere Sectie-eigenschappen
We hebben ook meer informatie verzameld over het berekenen van het traagheidsmoment van secties. Deze complete gids zou een uitgebreide kennisbasis moeten bieden voor alles wat te maken heeft met traagheidsmomenten, zwaartepunten, sectiemodulus en andere belangrijke geometrische sectie-eigenschappen. In de onderstaande segmenten, bespreken we wat het traagheidsmoment is, hoe je het zwaartepunt, en traagheidsmoment kunt berekenen en veelgebruikte MOI-vergelijkingen met behulp van de SkyCiv Traagheidsmoment en Zwaartepunt Calculator.
Wat is het Traagheidsmoment?
Het Traagheidsmoment (technisch bekend als het traagheidsmoment van oppervlakte, of het tweede oppervlakte moment) is een belangrijke geometrische eigenschap die in de bouwkunde wordt gebruikt. Het is direct gerelateerd aan de hoeveelheid materiaalsterkte die je sectie heeft.
Over het algemeen geldt, hoe hoger het traagheidsmoment, hoe meer sterkte je sectie heeft, en bijgevolg hoe minder het zal doorbuigen onder belasting. Het traagheidsmoment van een rechthoek, of welke vorm dan ook, s technisch gezien een meting van hoeveel koppel nodig is om de massa rond een as te versnellen - vandaar het woord traagheid in de naam.
Hoe het Traagheidsmoment te Berekenen - Rechthoekig
Om het traagheidsmoment van een rechthoek te berekenen, kun je de volgende formule gebruiken:
I = (b * h^3) / 12
I is het traagheidsmoment van de rechthoek
b is de breedte van de rechthoek
h is de hoogte van de rechthoek
Het is belangrijk op te merken dat de meeteenheid voor b en h consistent moet zijn (bijv., inches, millimeter, enz.). Ook is de eenheid van het eindresultaat afhankelijk van de invoereenheid, bijvoorbeeld als de invoer in meters is, dan is de eenheid van het resultaat m^4.
Voorbeeldberekening van het Traagheidsmoment
Laten we zeggen dat we een rechthoek hebben met de volgende afmetingen:
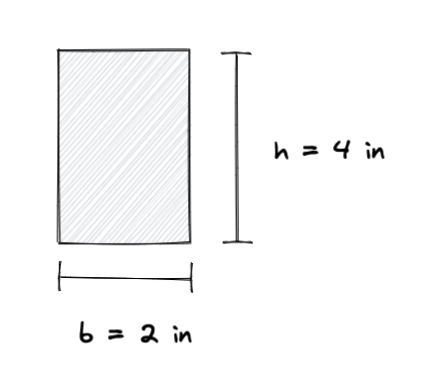
Met behulp van de formule voor het traagheidsmoment, kunnen we het traagheidsmoment van de rechthoek als volgt berekenen:
I = (b * h^3) / 12
I = (2 * 4^3) / 12
I = (2 * 64) / 12
= 10.67 in^4
Dus het traagheidsmoment van de rechthoek is 10.67 inch^4. Dit traagheidsmoment is rond de centroidale as, onthoud dat als je het traagheidsmoment over een andere as wilt vinden, je een andere formule moet gebruiken of een transformatie moet uitvoeren. Je kunt ook controleren dat de eenheid altijd het product is van de macht van de invoereenheid, in dit geval zijn alle invoereenheden inches, dus het resultaat is in inches^4.
We kunnen dit resultaat verifiëren met de bovenstaande gratis traagheidsmoment calculator, die hetzelfde resultaat van 10.6667 in^4:
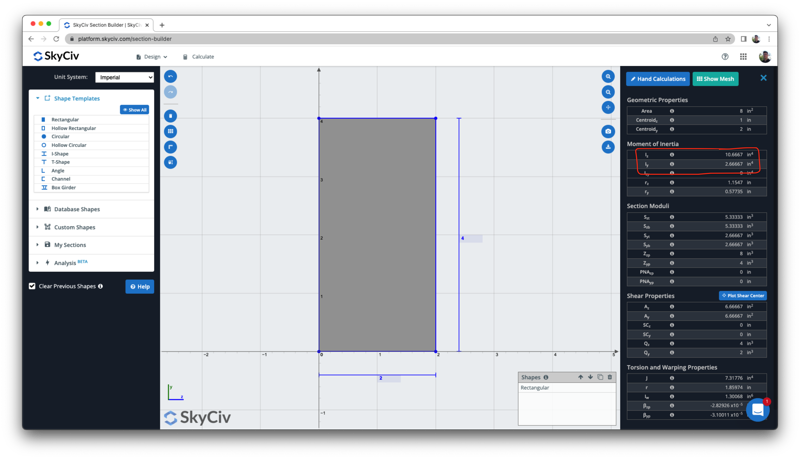
Hoe het Traagheidsmoment te Berekenen - I-balk
Laten we nu eens kijken naar een complexer geval waarbij de doorsnede een I-balk is, met verschillende flensafmetingen. Het concept is hetzelfde, maar de aanpak is in dit geval heel anders. Eigenlijk, we moeten de I-balk in feite beschouwen als een combinatie van verschillende rechthoeken en de verschillende delen optellen om het volledige traagheidsmoment van de sectie te krijgen. Kort gezegd, moeten we deze drie stappen volgen:
- Bereken de Neutrale As voor de gehele sectie
- Bereken het traagheidsmoment van elk deel
- Bereken het traagheidsmoment met behulp van de Parallelle As Stelling - wat in feite de som is van individuele traagheidsmomenten
Laten we dus de volgende sectie beschouwen:
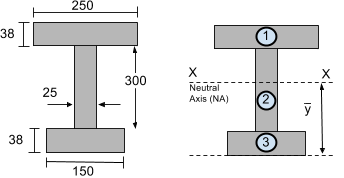
De Neutrale As (NA) bevindt zich op het zwaartepunt. Dit is in wezen een gewogen gemiddelde van de oppervlakte en afstand vanaf de onderkant voor elk segment. We hoeven alleen maar de zwaartepunt vergelijking te gebruiken om het verticale (j) waartepunt van een meersegmentvorm te berekenen.

We nemen de referentielijn vanaf de onderkant van de balksectie. Laten we nu Ai en yi vinden voor elk segment van de I-balk sectie die hierboven is weergegeven, zodat het verticale of y zwaartepunt kan worden gevonden.


Nu hebben we het zwaartepunt. We kunnen doorgaan met het berekenen van het traagheidsmoment. Om het totale traagheidsmoment van de sectie te berekenen, moeten we de "Parallelle As Stelling" gebruiken zoals hieronder gedefinieerd:

Omdat we het in drie rechthoekige delen hebben gesplitst, moeten we het traagheidsmoment van elk van deze secties berekenen. We kunnen nu de vereenvoudigde rechthoekige traagheidsmoment formule gebruiken:
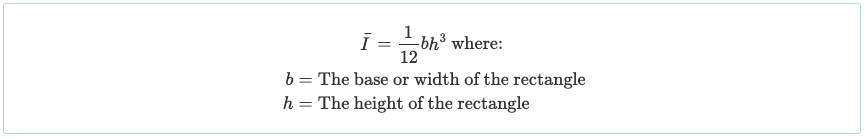
Nu hebben we alle informatie die we nodig hebben om de "Parallelle As Stelling" te gebruiken en het totale traagheidsmoment van de I-balk sectie te vinden. In ons traagheidsmoment voorbeeld:

Nogmaals, we kunnen dit resultaat vergelijken met dat van de gratis traagheidsmoment calculator om de resultaten, van zowel het zwaartepunt (216.29 in) als het traagheidsmoment (4.74 x 10^8 in^4) te vergelijken:
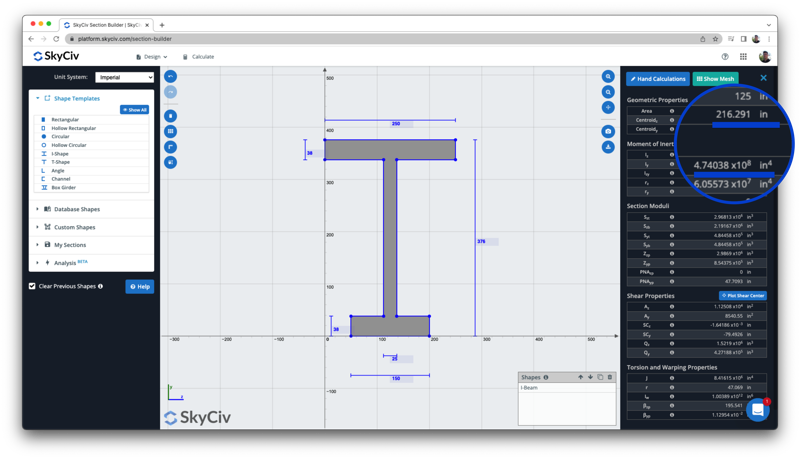
Voor meer informatie, bezoek onze tutorial op Het Berekenen van het Traagheidsmoment van een Balkdoorsnede.
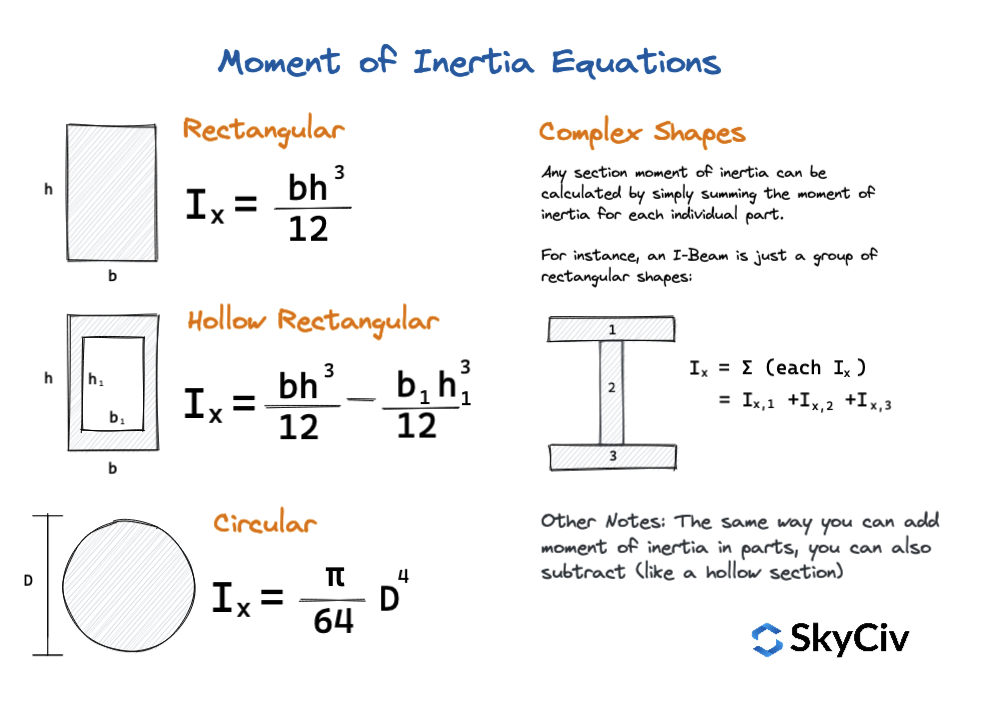
Traagheidsmoment Vergelijkingen
Eenvoudige vergelijkingen kunnen ook worden gebruikt om het traagheidsmoment van veelvoorkomende vormen en secties te berekenen. Dit zijn snelle traagheidsmoment vergelijkingen die snelle waarden bieden en een geweldige manier zijn om je resultaten te controleren of dubbel te controleren. Focussen op eenvoudige vormen, de onderstaande diagram toont enkele van deze vergelijkingen:
SkyCiv Zwaartepunt Calculator
Een zwaartepunt, ook wel het 'geometrische middelpunt' genoemd, is het zwaartepunt van een object met uniforme dichtheid. Een vereenvoudigde demonstratie van een zwaartepunt, zou de locatie zijn waar je een potlood moet plaatsen om het op je vinger te laten balanceren. De locatie waar het potlood in balans is en niet van je vinger valt, zou de geschatte locatie van het zwaartepunt van het potlood zijn. Het houdt rekening met de massa en dichtheid van het materiaal om het punt te bepalen waar de massa van het potlood gelijk is aan beide zijden van je vinger, en vertegenwoordigt dus het 'zwaartepunt' van het potlood.
De SkyCiv Zwaartepunt Calculator gebruikt FEA om zeer nauwkeurige resultaten in seconden te bieden, ongeacht hoe complex de vorm is. In de premium versie, kunnen gebruikers de coördinaten invoeren van de punten die de vorm definiëren en onze calculator geeft je de coördinaten van het zwaartepunt. Dit omvat de mogelijkheid om aangepaste vormen te ontwerpen via DXF-import, meerdere (opgebouwde) vormen en aangepaste puntvormen.
Naast de snelheid en nauwkeurigheid, is onze zwaartepunt calculator ook ongelooflijk eenvoudig te gebruiken. Met een eenvoudige gebruikersinterface, kun je je sectieafmetingen invoeren en je sectie-eigenschap waarden (inclusief het balksectie zwaartepunt) binnen enkele seconden ontvangen. Of je nu werkt aan een ontwerpproject, experimenteert met verschillende secties of studeert voor een examen, de SkyCiv Zwaartepunt Calculator is de perfecte tool om je te helpen de klus te klaren.
Sectiemodulus Calculator
Zoals eerder opgemerkt, biedt deze gratis tool je ook een berekening van de Elastische Sectiemodulus, maar als je net begint als ingenieur, begrijp je misschien niet wat de Sectiemodulus is. Simpel gezegd, de sectiemodulus is een sectie-eigenschap van een doorsnede die de weerstand tegen buiging meet en berekend wordt als de verhouding van het traagheidsmoment tot de afstand van de neutrale as tot de meest verre vezel. De Elastische Sectiemodulus wordt in deze vergelijking eenvoudigweg weergegeven als:
Waarbij,
- S de sectiemodulus is
- I het traagheidsmoment van de sectie over de neutrale as is
- y de afstand van de neutrale as tot het meest verre punt van de sectie is
Er zijn twee soorten Sectiemodulus: Elastisch en Plastisch. In Amerika, wordt S meestal gebruikt om te verwijzen naar de Elastische Sectiemodulus terwijl Z wordt gebruikt om te verwijzen naar de Plastische Sectiemodulus. In Groot-Brittannië en Australië, zijn deze meestal omgekeerd. De Elastische Sectiemodulus wordt meestal aangeduid met de letter Z, terwijl de Plastische Sectiemodulus wordt aangeduid met de letter S.
Over het algemeen, wordt de Elastische Sectiemodulus gebruikt voor sectieontwerp omdat deze toepasbaar is tot het vloeipunt voor de meeste metalen. Metalen worden meestal niet ontworpen om voorbij het vloeipunt van het materiaal te gaan.
Aanvullende Documentatie
Raadpleeg de volgende documentatiepagina's voor meer gedetailleerde informatie over het traagheidsmoment, hoe je deze kunt berekenen voor verschillende vormen, en hoe je onze zwaartepunt calculator kunt gebruiken:
Meer gratis tools beschikbaar
SkyCiv biedt ook andere tools zoals de I-balk maat tool en gratis structurele ontwerpsoftware. De dynamische sectietekening toont ook een grafische weergave van je balksectie. Dus als je het traagheidsmoment van een cirkel, traagheidsmoment van een rechthoek of andere vormen wilt berekenen, gebruik dan gerust de onderstaande software of onze allesomvattende SkyCiv Section Builder.
SkyCiv biedt een breed scala aan Cloud Structurele Analyse en Ontwerp Software voor ingenieurs. Als een voortdurend evoluerend technologiebedrijf, zijn we toegewijd aan het innoveren en uitdagen van bestaande workflows om ingenieurs tijd te besparen in hun werkprocessen en ontwerpen.
Meer functionaliteit nodig?
Upgrade naar een professioneel plan account om alle functies te ontgrendelen