Heeft u zich wel eens afgevraagd hoe structurele software in wezen werkt? Blijf gewoon lezen, en je zult zien hoe we het SkyCiv-platform en Python-programmering kunnen gebruiken door middel van een voorbeeld dat is ontwikkeld in een klaslokaal van structurele analyse.
Een snel overzicht van structurele analyse
We gebruiken vaak beschikbare software om een structurele analyse op te lossen, wat resulteert in krachten, verplaatsing, benadrukt, enzovoort. In simpele termen, het probleem valt in de volgende vorm:F=K∙d
F=K∙d
Waarbij:
- F is de vectorkrachten
- K is de structuurstijfheid
- d is het verplaatsingsveld
Het belangrijkste doel is om een continue structuur om te zetten in discrete “stukken” van een samenstel en analyseer het, verkrijgen van krachten en verplaatsingen. Er moet een algemeen pad worden gevolgd:
- Voorverwerken: de eerste stap in structurele analyse, waar we de structuurgegevens krijgen, geometrie, materiaaleigenschappen:, en laadt en voltooit wanneer de global stijfheidsmatrix is gebouwd.
- Proces: waar we de vorige uitdrukking oplossen, F=K∙d F=K∙d. Sommige methoden die algemeen worden aanvaard om het systeem van lineaire vergelijkingen op te lossen, zijn Gauss-Jordan, Gaussiaanse eliminatie, enzovoort.
- Nabewerking: het laatste deel om de resultaten weer te geven in termen van krachten en stress, National Design Specification Standards® voor houtconstructie.
Voorbeeld van een vlak frame
Het kastvoorbeeld bestaat uit een normaal vlak frame (Figuur 1).
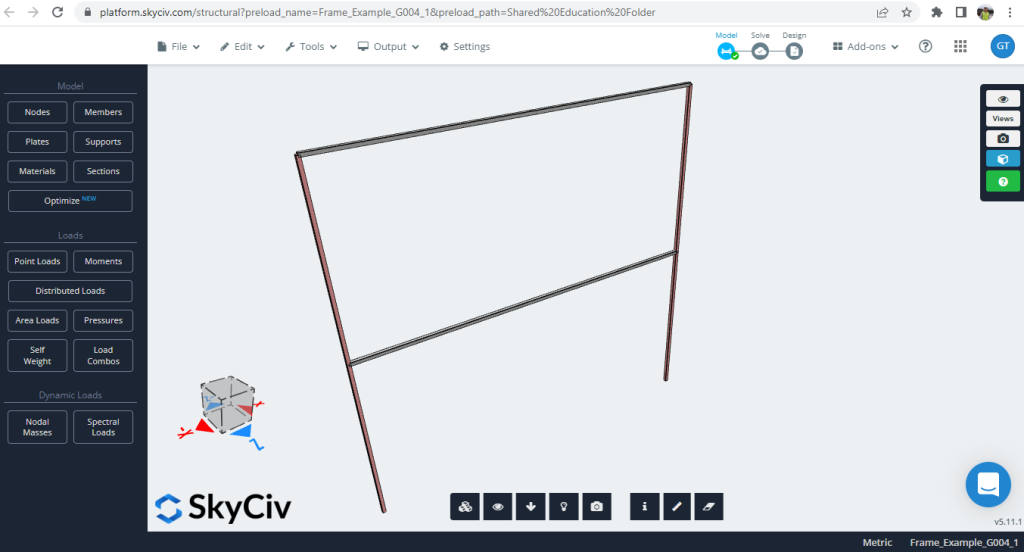
Figuur 1. Structureel 2D-framevoorbeeld
De eigenschappen van het element voor kolommen, balken, en materialen zijn:
| Structureel element | Oppervlakte, (mm^2) | Luiheid, (mm^4) |
|---|---|---|
| Kolommen | 93,000 | 720,000,000 |
| Balken | 140,000 | 2,430,000,000 |
Concrete eigenschappen:
- Materiaalsterkte, f'c=20MP.een f′c=20 MPa
- Young's Modulus, E=17000MP.een E=17000MPa
Python-programmering en SkyCiv-modellering
Dit is het moment om parallel te gaan werken met modellering in Python en SkyCiv. Figuur 2 toont de ingevoerde gegevens (knooppunten, elementen, graden van vrijheid, oriëntatie van de lokale as) voor de code ontwikkeld in Python. U kunt het bestand zelf controleren en het voorbeeld hier doorheen halen link.
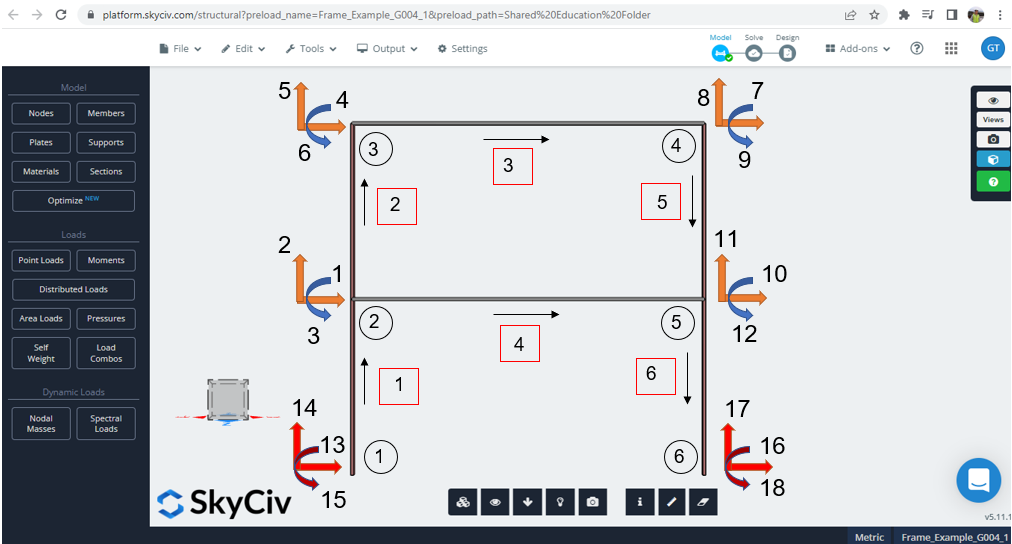
Figuur 2. Lokale stijfheidsmatrixfunctie
Het Python-bestand gebruikt een functioneel programmeerparadigma omdat het gemakkelijk uit te leggen en te ontwikkelen is in de klas. Dit bestaat uit delen en heersen, het modulariseren van de codeconstructie en zijn methoden.
Bij het coderen van de methode, het belangrijkste is het definiëren van de toe te passen wiskundige formulering. We zullen de Euler Bernoulli Beam gebruiken:
De verschillen in waarden (Python-script en SkyCiv S3D) zijn gering, met ongeveer 2.90% als het gemiddelde.
2. Axiale krachten
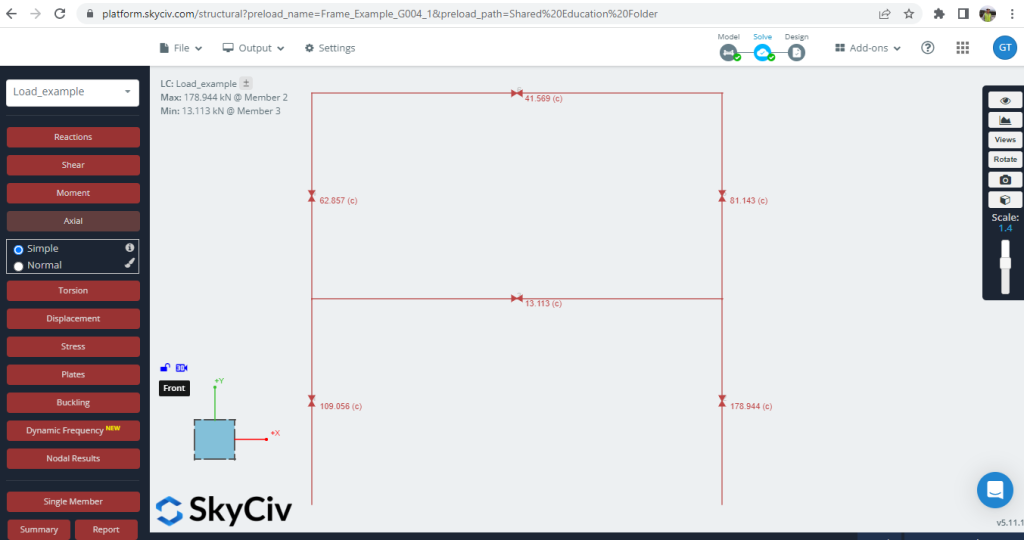
Figuur 5. Axiale krachten ontwikkelden zich in het frame
| Q, kN, SkyCiv | Q, kN, Python-script | (Delta )% |
|---|---|---|
| 109.056 | 109.519 | 0.423 |
| 62.857 | 62.616 | 0.383 |
| 41.589 | 43.252 | 3.845 |
| 13.113 | 11.709 | 10.707 |
| 81.143 | 81.384 | 0.296 |
| 178.944 | 178.480 | 0.2593 |
De verschillen in waarden (Python-script en SkyCiv S3D) zijn gering, met ongeveer 2.65 % als het gemiddelde.
3. Afschuifkrachten
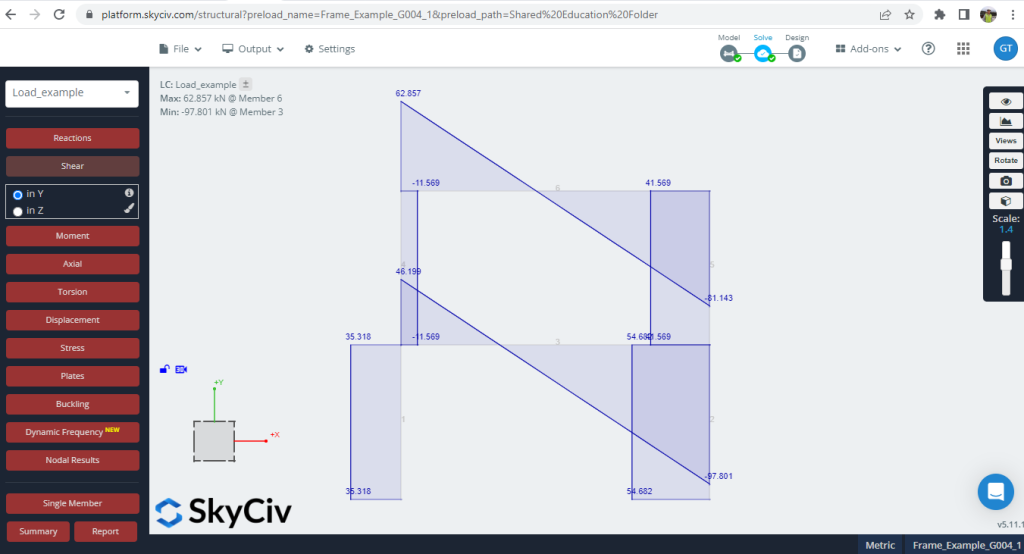
Figuur 6. Dwarskrachten ontwikkelden zich in het frame
| Q, kN, SkyCiv | Q, kN, Python-script | (Delta )% |
|---|---|---|
| 35.318 | 35.039 | 0.790 |
| 35.318 | 35.039 | 0.790 |
| -11.569 | 13.252 | 12.700 |
| -11.569 | 13.252 | 12.700 |
| 62.857 | 62.616 | 0.383 |
| -81.143 | -81.384 | 0.296 |
| 46.199 | 46.903 | 1.501 |
| -97.801 | -97.097 | 0.720 |
| 41.569 | 43.252 | 3.891 |
| 41.569 | 43.252 | 3.891 |
| 54.682 | 54.961 | 0.508 |
| 54.682 | 54.961 | 0.508 |
De verschillen in waarden (Python-script en SkyCiv S3D) zijn gering, met ongeveer 3.22% als het gemiddelde.
4. Buigende momenten
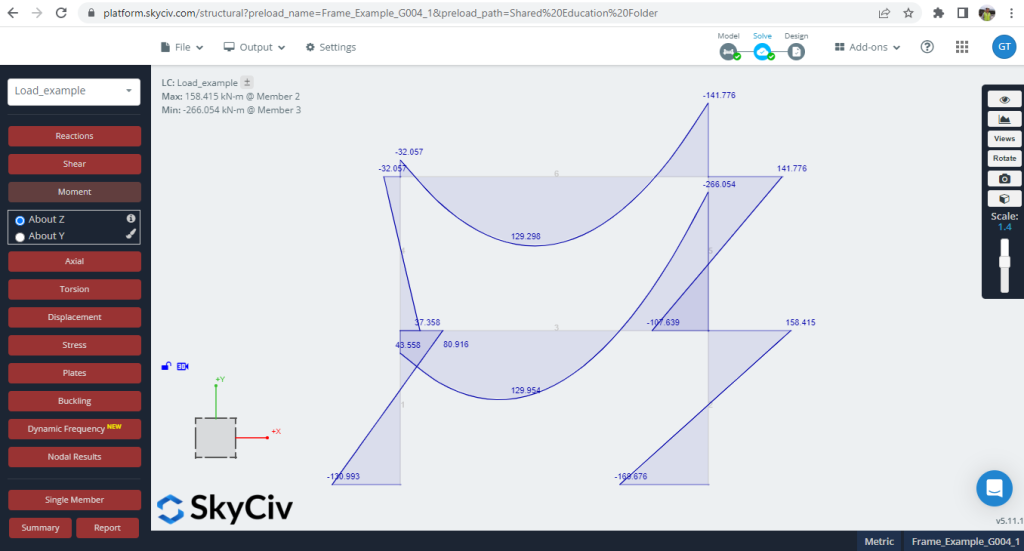
Figuur 7. Momenten ontwikkelden zich in het frame
| Q, kN-m, SkyCiv | Q, kN-m, Python-script | (Delta )% |
|---|---|---|
| -130.993 | -133.213 | 1.667 |
| 80.916 | 77.022 | 4.812 |
| 37.358 | 42.713 | 12.537 |
| -32.057 | -36.797 | 12.881 |
| -32.057 | -36.797 | 12.881 |
| -141.776 | -149.400 | 5.103 |
| 43.558 | 34.309 | 21.234 |
| -266.054 | -266.859 | 0.302 |
| 107.639 | 110.109 | 2.243 |
| -141.776 | -149.400 | 5.103 |
| 169.676 | 173.016 | 1.930 |
| -158.415 | -156.749 | 1.052 |
De verschillen in waarden (Python-script en SkyCiv S3D) zijn gering, met ongeveer 6.81% als het gemiddelde.
5. Gevolgtrekking
Dit bericht heeft gediend als een test dat de SkyCiv-platform is een uitstekende bron voor educatieve doeleinden vanwege zijn krachtige capaciteiten in structurele analyse. Python-programmering gebruiken en de resultaten vergelijken met nauwkeurige software zoals SkyCiv, is een must dat elke technische cursus in de kerninhoud moet opnemen.


