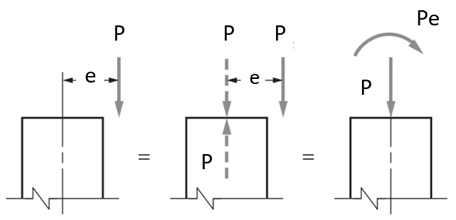
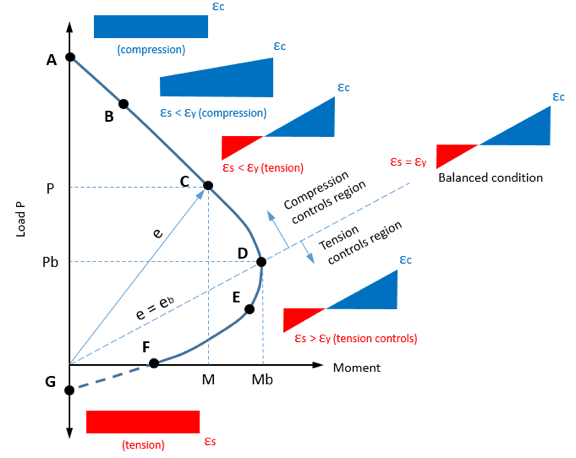
 Beispiel einer Interaktionskurve
Beispiel einer Interaktionskurve- Reine axiale Kompression (Punkt A.). Dies ist die größte axiale Druckbelastung, die die Säule tragen kann.
- Kompression mit geringfügiger Biegung (Punkt B.). Dies ist der Fall bei einer großen axialen Last, die bei einer kleinen Exzentrizität wirkt. Die Spannungsverteilung wird geneigt, aber der Abschnitt wird immer noch komprimiert. Ein Versagen tritt durch Zerkleinern des Betons auf.
- Kompressionskontrolle (Punkt C.). Hier existieren sowohl Druckzone als auch Spannungszone von Beton. Stahl ist Spannung ausgesetzt. Ein Versagen tritt durch Quetschen des Betons auf der Kompressionsseite auf, wohingegen die Spannung in Stahl fs geringer ist als die Fließspannung fy.
- Ausgewogener Zustand (Punkt D.). Ein ausgeglichener Zustand ist erreicht, wenn die Druckspannung im Beton begrenzt ist und die Zugbewehrung gleichzeitig nachgibt. Das Versagen von Beton tritt gleichzeitig mit den Stahlausbeuten auf.
- Spannungsregelung (Punkt E.). Dies ist der Fall bei einer kleinen axialen Last mit großer Exzentrizität, das ist, ein großer Moment. Bei Misserfolg, Die Dehnung im Spannstahl ist größer als die Streckdehnung.
- Reine Biegung (Punkt F.). Der Abschnitt ist in diesem Fall einem Biegemoment M ausgesetzt, wohingegen die axiale Last P = ist 0. Ein Fehler tritt auf wie bei einem Balken, der nur einem Biegemoment ausgesetzt ist.
- Reine axiale Spannung (Punkt G.). Dies ist die größte axiale Zuglast, die die Säule tragen kann.
- Dehnungen in Beton und Stahl sind proportional zum Abstand von der neutralen Achse
- Das Kräftegleichgewicht und die Dehnungsverträglichkeit müssen erfüllt sein
- Die maximal nutzbare Druckspannung in Beton beträgt 0.003
- Die Zugfestigkeit von Beton kann vernachlässigt werden
- Der Betonspannungsblock kann als rechteckige Form angenommen werden
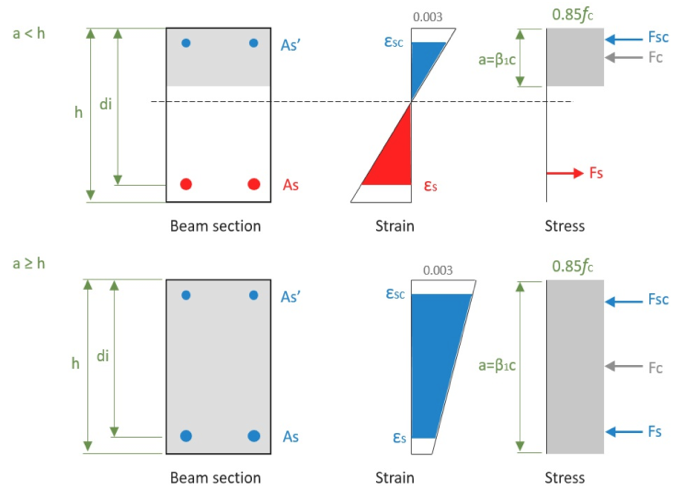

Interpretation der Interaktionskurve
Damit das Design einer Säule als angemessen angesehen wird (sicher), die Kombination von Aktionseffekten (M., P.) muss kleiner sein als die Kombination der Designstärken (M., P.) aus der Interaktionskurve. Dies bedeutet, dass, wenn die Position des M.,Der P-Punkt auf dem Plot liegt außerhalb der Kurve. Es wird davon ausgegangen, dass er diese Kriterien nicht erfüllt und als unsicher eingestuft wird.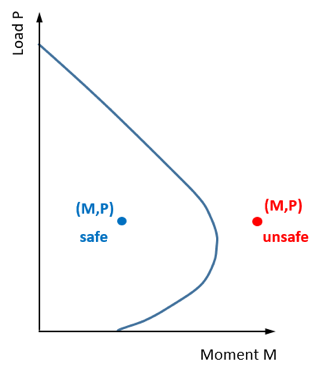
SkyCiv Stahlbetonkonstruktion
SkyCiv bietet eine voll ausgestattete Stahlbetonkonstruktion Software, mit der Sie die Betonbalken- und Betonsäulenkonstruktionen gemäß überprüfen können ACI 318, AS 3600 und EN2 Gestaltungsnormen. Die Software ist einfach zu bedienen und vollständig Cloud-basiert; Für den Start ist keine Installation oder kein Download erforderlich!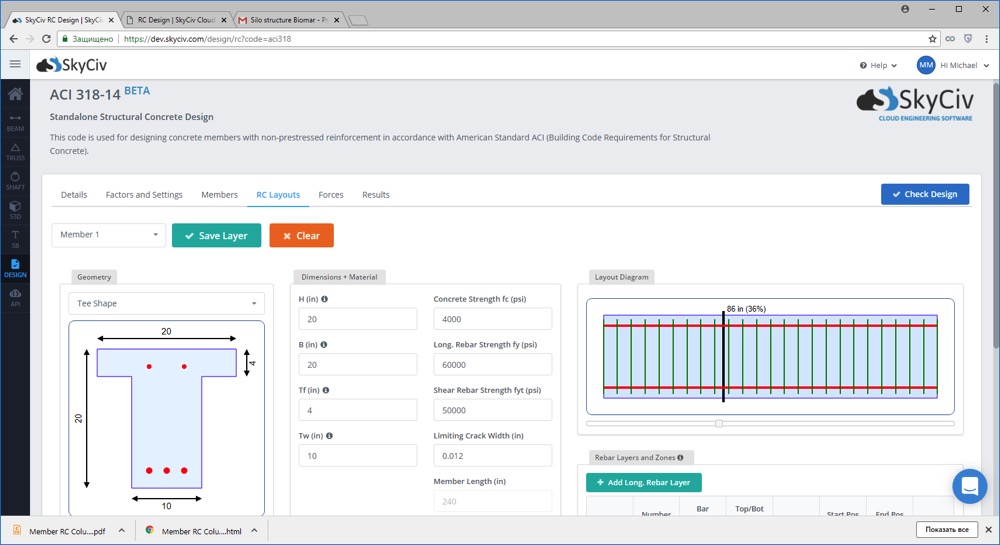
Michael Malgin
Statiker, Produktentwicklung
MEng (Bürgerlich)
[email protected]
Statiker, Produktentwicklung
MEng (Bürgerlich)
[email protected]



