Haben Sie sich schon einmal gefragt, wie Struktursoftware im Wesentlichen funktioniert?? Lesen Sie einfach weiter, und Sie werden anhand eines Beispiels, das in einem Klassenzimmer für Strukturanalyse entwickelt wurde, herausfinden, wie wir die SkyCiv-Plattform und die Python-Programmierung verwenden können.
Ein kurzer Überblick über die Strukturanalyse
Wir verwenden häufig verfügbare Software, um eine Strukturanalyse zu lösen, was zu Kräften führt, Verschiebung, betont, etc. In einfachen Worten, das Problem fällt in die folgende Form:F.=K.∙d
F=K∙d
Wo:
- F sind die Vektorkräfte
- K ist die Struktursteifigkeit
- d ist das Verschiebungsfeld
Das Hauptziel besteht darin, eine kontinuierliche Struktur in eine diskrete umzuwandeln “Stücke” einer Baugruppe und analysieren diese, Kräfte und Verschiebungen erhalten. Es muss ein allgemeiner Weg beschritten werden:
- Vorbereiten: der erste Schritt in der Strukturanalyse, woher wir die Strukturdaten bekommen, Geometrie, den Materialeigenschaften, und lädt und finalisiert, wenn das globale Steifigkeitsmatrix ist konstruiert.
- Verfahren: wo wir den vorherigen Ausdruck lösen, F.=K.∙d F=K∙d. Einige allgemein anerkannte Methoden zur Lösung des linearen Gleichungssystems sind Gauß-Jordan, Gaußsche Elimination, etc.
- Nachbearbeitung: der letzte Teil, um die Ergebnisse in Bezug auf Kräfte und Spannungen anzuzeigen, Entwurfsbestimmungen für beide zulässige Spannungsbemessungen einbeziehen.
Beispiel für einen ebenen Rahmen
Das Fallbeispiel besteht aus einem regelmäßigen ebenen Rahmen (Abbildung 1).
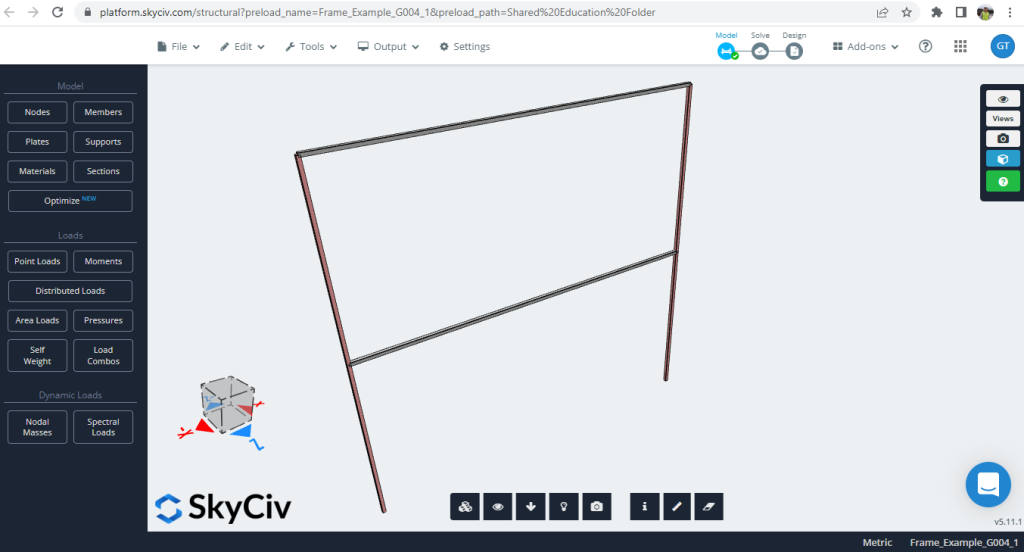
Abbildung 1. Beispiel für einen strukturellen 2D-Rahmen
Die Eigenschaften des Elements für Spalten, Balken, und Materialien sind:
| Strukturelement | Bereich, (mm^2) | Trägheit, (mm^4) |
|---|---|---|
| Säulen | 93,000 | 720,000,000 |
| Träger | 140,000 | 2,430,000,000 |
Konkrete Eigenschaften:
- Materialstärke, f'c=20M.P.ein f′c=20MPa
- Elastizitätsmodul, E.=17000M.P.ein E=17000 MPa
Python-Programmierung und SkyCiv-Modellierung
Jetzt ist es an der Zeit, parallel zur Modellierung in Python und SkyCiv zu arbeiten. Abbildung 2 zeigt die Eingabedaten (Knoten, Elemente, Freiheitsgrade, lokale Achsenorientierung) für den in Python entwickelten Code. Sie können die Datei selbst überprüfen und das Beispiel durch diese ausführen link.
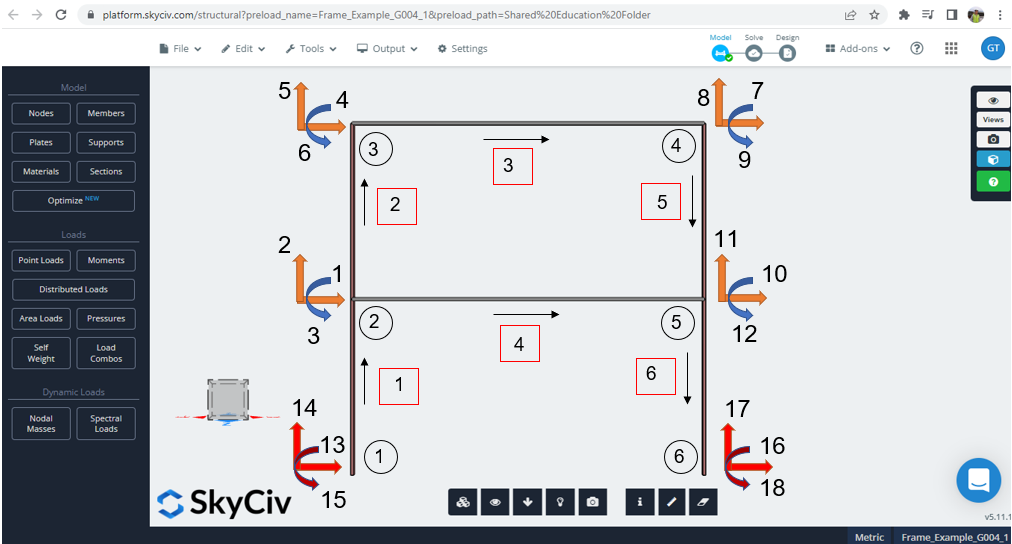
Abbildung 2. Funktion der lokalen Steifigkeitsmatrix
Die Python-Datei verwendet ein funktionales Programmierparadigma, da es im Unterricht einfach zu erklären und zu entwickeln ist. Diese besteht aus Teilen und Erobern, Modularisierung der Codekonstruktion und ihrer Methoden.
Beim Codieren der Methode, Das Wichtigste ist, die anzuwendende mathematische Formulierung zu definieren. Wir verwenden den Euler-Bernoulli-Balken:
Die Werteunterschiede (Python-Skript und SkyCiv S3D) sind gering, mit ca 2.90% als Mittelwert.
2. Axialkräfte
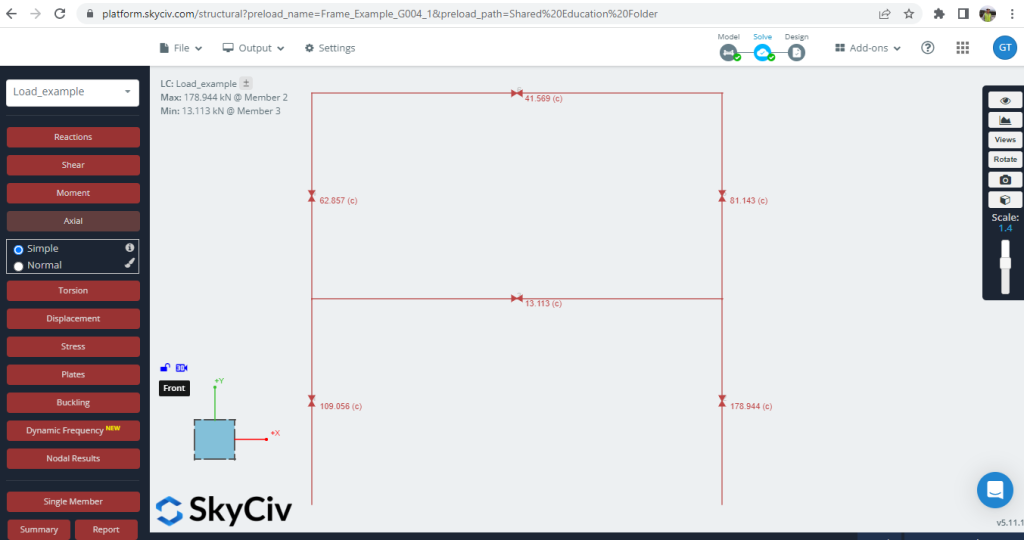
Abbildung 5. In den Rahmen entwickelte Axialkräfte
| Q., kN, SkyCiv | Q., kN, Python-Skript | (p-Delta-Effekte )% |
|---|---|---|
| 109.056 | 109.519 | 0.423 |
| 62.857 | 62.616 | 0.383 |
| 41.589 | 43.252 | 3.845 |
| 13.113 | 11.709 | 10.707 |
| 81.143 | 81.384 | 0.296 |
| 178.944 | 178.480 | 0.2593 |
Die Werteunterschiede (Python-Skript und SkyCiv S3D) sind gering, mit ca 2.65 % als Mittelwert.
3. Scherkräfte
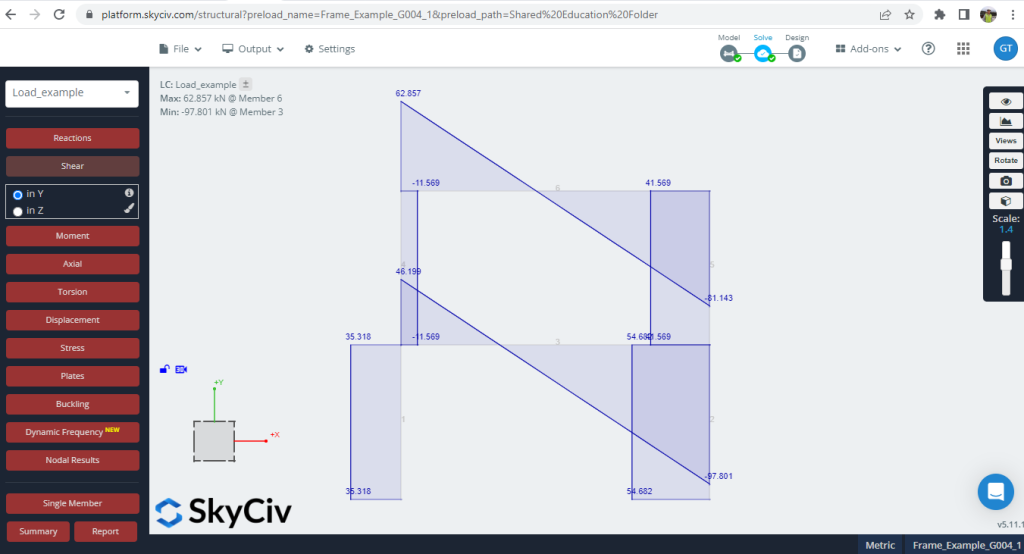
Abbildung 6. Es entwickelten sich Scherkräfte im Rahmen
| Q., kN, SkyCiv | Q., kN, Python-Skript | (p-Delta-Effekte )% |
|---|---|---|
| 35.318 | 35.039 | 0.790 |
| 35.318 | 35.039 | 0.790 |
| -11.569 | 13.252 | 12.700 |
| -11.569 | 13.252 | 12.700 |
| 62.857 | 62.616 | 0.383 |
| -81.143 | -81.384 | 0.296 |
| 46.199 | 46.903 | 1.501 |
| -97.801 | -97.097 | 0.720 |
| 41.569 | 43.252 | 3.891 |
| 41.569 | 43.252 | 3.891 |
| 54.682 | 54.961 | 0.508 |
| 54.682 | 54.961 | 0.508 |
Die Werteunterschiede (Python-Skript und SkyCiv S3D) sind gering, mit ca 3.22% als Mittelwert.
4. Biegemomente
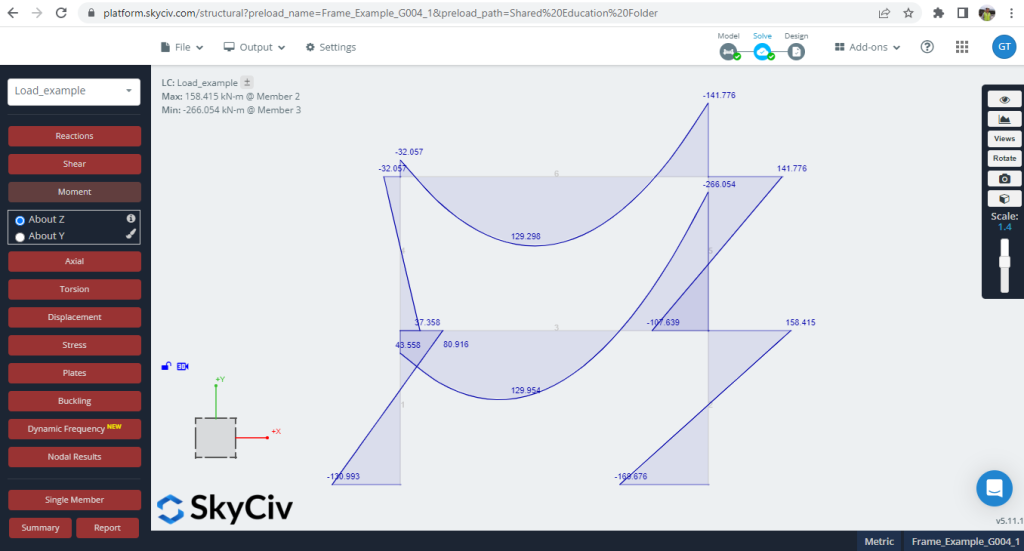
Abbildung 7. In den Rahmen entwickelte Momente
| Q., kN-m, SkyCiv | Q., kN-m, Python-Skript | (p-Delta-Effekte )% |
|---|---|---|
| -130.993 | -133.213 | 1.667 |
| 80.916 | 77.022 | 4.812 |
| 37.358 | 42.713 | 12.537 |
| -32.057 | -36.797 | 12.881 |
| -32.057 | -36.797 | 12.881 |
| -141.776 | -149.400 | 5.103 |
| 43.558 | 34.309 | 21.234 |
| -266.054 | -266.859 | 0.302 |
| 107.639 | 110.109 | 2.243 |
| -141.776 | -149.400 | 5.103 |
| 169.676 | 173.016 | 1.930 |
| -158.415 | -156.749 | 1.052 |
Die Werteunterschiede (Python-Skript und SkyCiv S3D) sind gering, mit ca 6.81% als Mittelwert.
5. Fazit
Dieser Beitrag hat als Test gedient, dass die SkyCiv-Plattform ist aufgrund seiner leistungsstarken Kapazitäten in der Strukturanalyse eine hervorragende Ressource für Bildungszwecke. Verwendung von Python-Programmierung und Vergleich der Ergebnisse mit genauer Software wie SkyCiv, ist ein Muss, das jeder Ingenieurkurs in seinen Kerninhalt aufnehmen muss.


