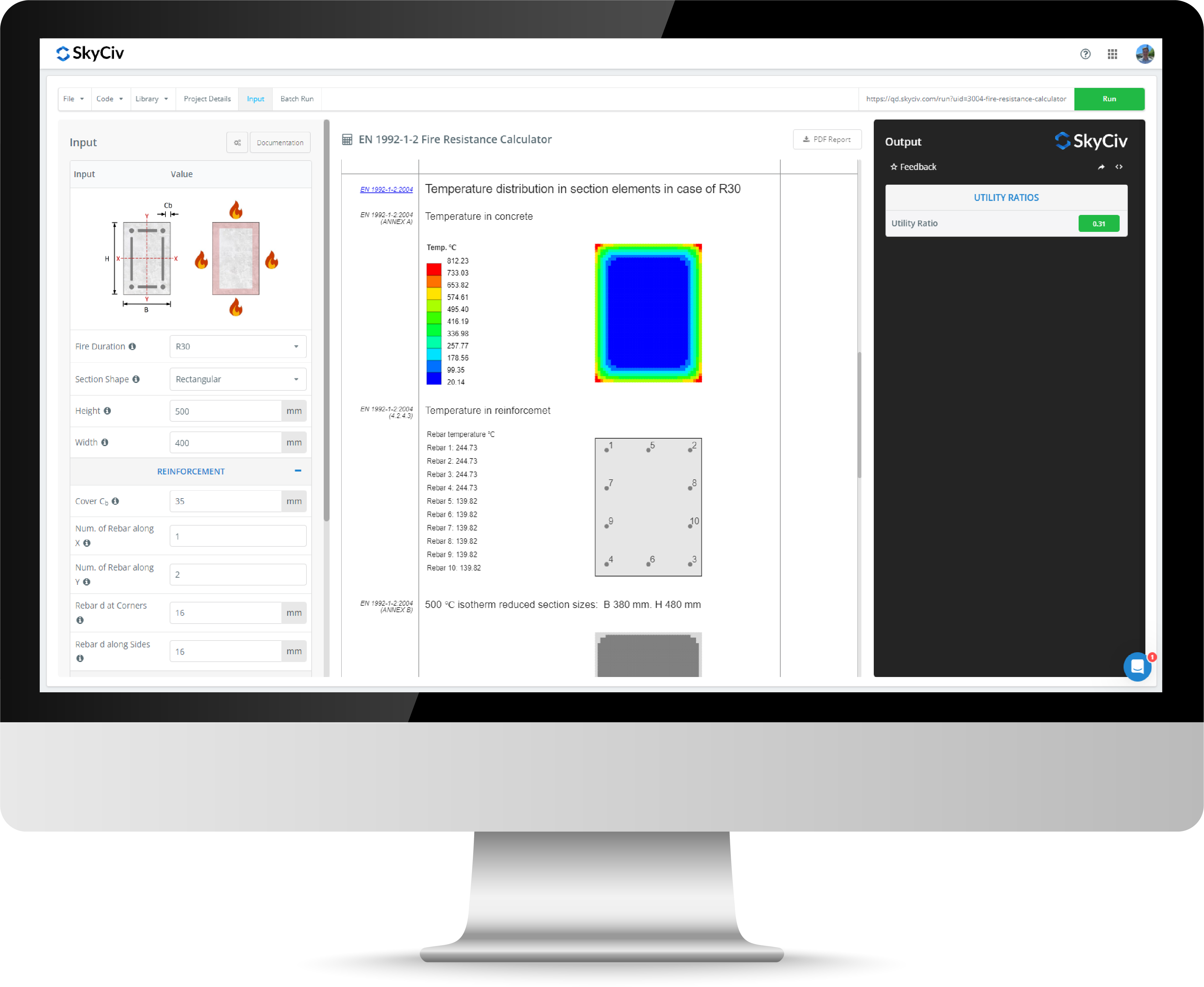
鉄筋コンクリートカラム設計計算機
SkyCIV鉄筋コンクリートカラム計算機により、エンジニアは円形および長方形のコンクリートカラムの鉄筋コンクリートカラム設計をACIに記入できます。, ヨーロッパ人, およびオーストラリアの基準. 鉄筋コンクリートの柱は、コンクリートと鋼の利点を経済的に組み合わせた複合セクションです. 鉄筋コンクリートコラムの複合性により、設計計算により他のセクションよりも厳密になり、クイックデザインのコンクリートカラム計算機は、エンジニアが能力を評価し、相互作用図を生成するための簡単なツールを提供します。 次の基準:
- アメリカ - ACI-318-19: 構造コンクリートの建築基準要件.
- オーストラリア規格 - なので 3600-2018: コンクリート構造物, 鋼 & 腱.
- ヨーロッパの基準 - ユーロコード 2: コンクリート構造物の設計 (に 1992-1-1:2004).
- ニュージーランドの基準 - NZS 3101:2006: コンクリート構造物の設計
これらの標準をに切り替えることができます コンクリート計算機の右上 左側の入力パネルの上部にあるフラグアイコンを使用する. 電卓を実行するには, ソフトウェアの右上にある実行ボタンを押します.
コンクリートの柱の設計について
列とは何ですか?
柱は建物内の垂直メンバーであり、建物内の荷物がその基礎に移動できるようにするための鍵です. 垂直メンバーとして, 彼らは主に重力力のために大きな圧縮荷重を扱っていますが、自然に負荷の偏心や風や地震荷重などの横方向の力のために、曲げモーメントに抵抗するためにも必要です. 柱は杭に非常に似ていますが、杭には座屈に対する抑制に役立つ土壌があり、柱としてその基部に力が抵抗するパイルのシャフトに沿って力を解決する可能性があります。. 杭にはほとんど常に円形のセクションがありますが、具体的な柱には一般的に円形または長方形の断面があります.
コンクリート列を使用する理由?
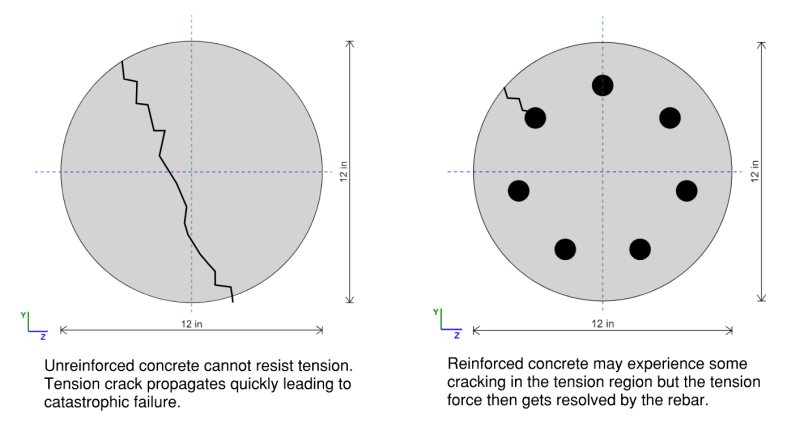
柱は大きな圧縮力にさらされているため、自然にコンクリートを使いたくなります, 圧縮負荷を扱うための非常に経済的なソリューション. 残念ながら, プレーンコンクリートは脆く、張力と曲げが弱いため、鉄の補強材なしで使用するのが安全ではありません (鉄筋).
鉄筋コンクリート柱は、経済的な柱の設計にコンクリートの圧縮強度と鉄筋の張力強度を利用します. コンクリートの柱は、耐久性のために建設に広く使用されています, 耐火性, 重い負荷をサポートする能力.
鉄筋コンクリート柱の設計方法
強化された列の複合性により、第一原則から分析することがより困難になります. スチールを使用すると、セクションのモジュラスを単純に計算し、それを降伏強度を掛けて曲げ容量を見つけることができます. 鉄筋コンクリートを使用すると、セクションは均一ではなく、2つの異なる材料を使用する.
これは、柱の容量に影響を与える列がほとんど常に曲がっていると同時に作用すると考えると、より困難になります。. そのようなデザインを支援するツールは、相互作用図として知られています.
相互作用図とは何ですか ?
相互作用図は、曲げ荷重と軸荷重を組み合わせた列の強度容量のグラフィカルな表現です.
この記事の次のセクションでは、手作業で強化された列の相互作用図を計算する方法について説明します. 相互作用図を生成する原則をフォローすると、読者は相互作用図のキーポイントをよりよく理解し、具体的な列のデザインの相互作用図の結果を解釈する方法をよりよく理解します。.
すべての列セクションの手で相互作用図を生成することは時間がかかる可能性があるため、SkyCIVコンクリートカラム計算機のようなソフトウェアが存在して、コンクリート列の相互作用図を自動的に生成し、ユーザーが相互作用図を手動で確認することなく設計負荷に基づいて利用を評価します。.
相互作用図を作成する方法
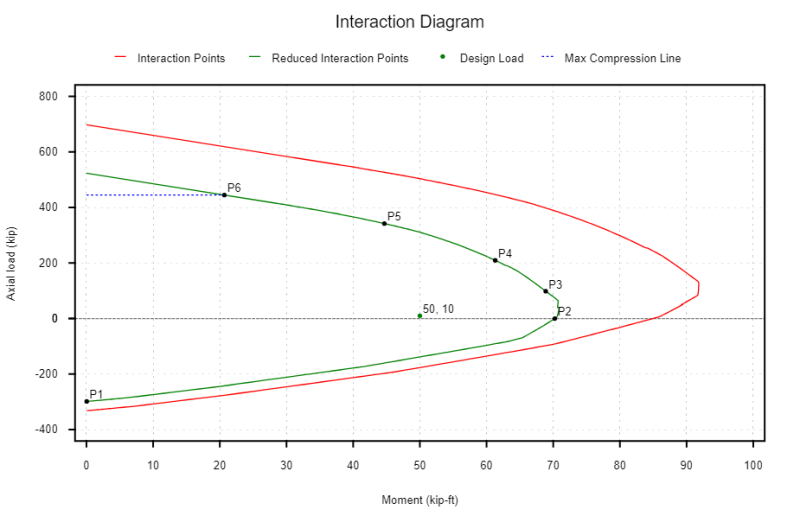
相互作用図を作成するには、次の場合の鉄筋コンクリート列を評価することが含まれます:
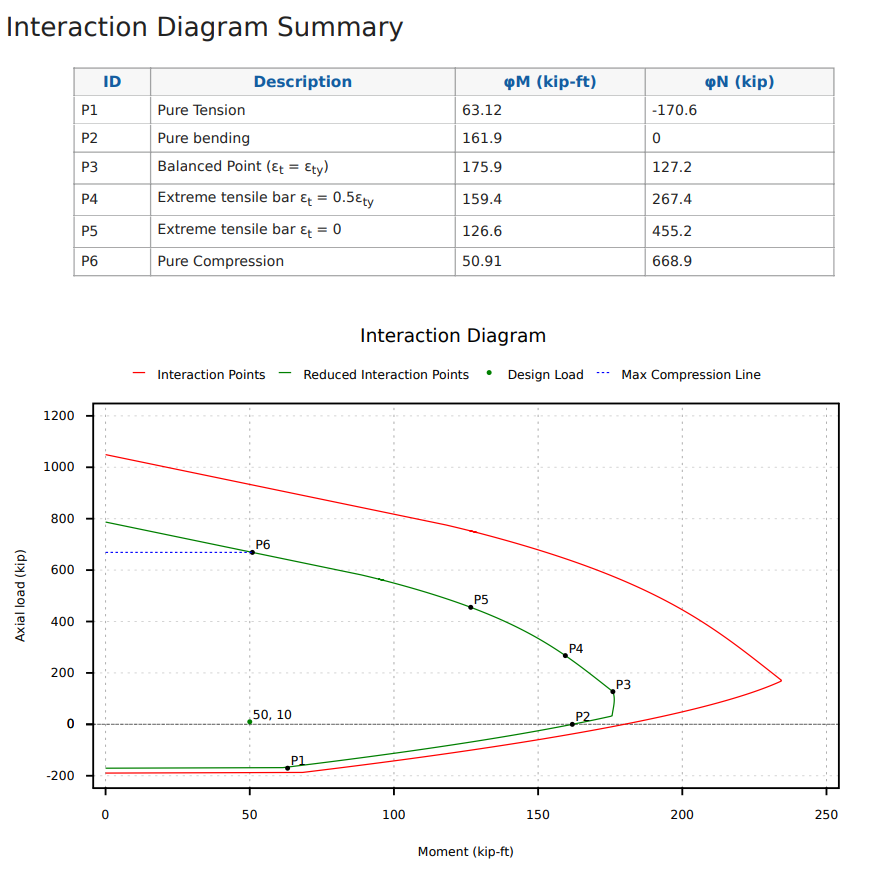
- (P1) 純粋な緊張 - これは、柱がサポートできる最大の軸方向引張荷重です。.
- (P2) 純粋な曲げ - セクションは、曲げモーメントmとp =の軸力の対象となります 0
- (P3) バランスポイント (et = eタイ) - 極端な引張鋼の収量と同時にコンクリートの故障が発生すると、バランスのとれた状態に達します.
- (P4) ハーフイールドポイント (et = 0.5 eタイ) - これは、正確な相互作用図をプロットするのに役立つ中間位置です.
- (p5) 減圧点 (et = 0) - このケースは、緊張ラップスプライスが圧縮ラップスプライスに変更されるときの位置をマークします (ACI). バーは、圧縮力のみを摂取するために張力をかけるためにいくつかの張力をとる間に移行しています.
- (p6) 純粋な圧縮 - これは、柱がサポートできる最大の軸方向圧縮荷重です。.
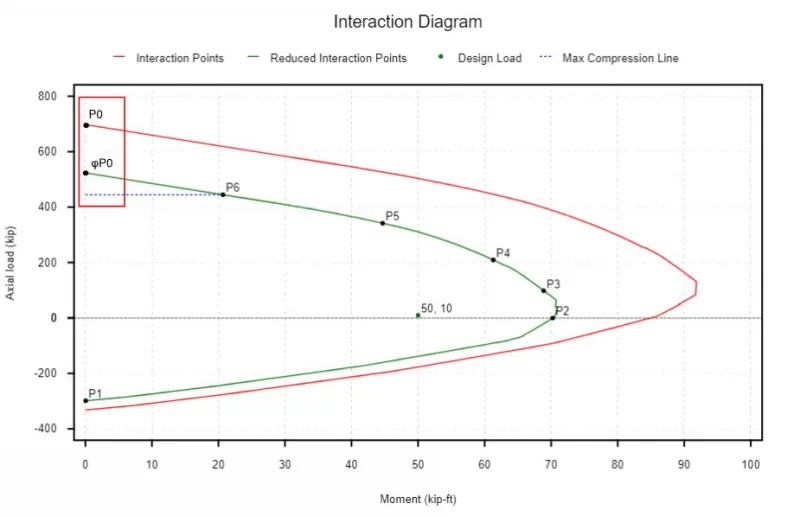
私たちの相互作用図は、設計に必要な安全削減係数も考慮することができます. 上記の相互作用図で気付くかもしれないことは、圧縮制御領域に安全性が大きいことです (0.65 または 0.75) 緊張制御領域で行うよりも (0.9).
ACIによる具体的なカラム設計の還元因子 318-19
強度削減係数 (ファイ) 今のところ使用されています, 軸方向の力または結合モーメントと軸方向の力は、セクションの分類方法に依存しています.
セクションは、正味引張株に関連して分類されます (et) これは、緊張面に最も近い補強の緊張です:
- 緊張が制御されました : et ≥eタイ + 0.003
- 遷移 : eタイ < et < eタイ + 0.003
- 圧縮制御εt <= eタイ
強度削減係数の変化のため、圧縮制御ポイントを手で計算することも役立つかもしれません (前の図のP3) 張力制御点 (et ≥eタイ + 0.003) ラベル付けされていません.
また、横方向の補強にも依存しています. 確認するスパイラルのために 25.7.3 εに基づいてPHIを入手できますt なので:
- 緊張が制御されました: φ = 0.9
- 圧縮制御: φ = 0.75
- 遷移: φ = 0.75 + 0.15 (et - eタイ ) / 0.003
他のタイプの横方向の補強:
- 緊張が制御されました - φ = 0.9
- 圧縮制御 - φ = 0.65
- 遷移=φ= 0.65 + 0.25 (et - eタイ ) / 0.003
(実際、遷移式は、圧縮または張力制御ポイントにどれだけ近いかに依存する単純な線形関数です。)
コンクリート柱の純粋な圧縮能力を計算する方法
純粋な圧縮能力またはスカッシュ荷重は、純粋な軸方向の負荷の下での柱の強度です.
ACIを使用します 318-19 セクション 22.4.2 次の式を使用して、コンクリート列の純粋な圧縮荷重を計算できます:
p0 = 0.85 f 'c * (あg - あst) + fそして * あst
どこ:
- f 'c 具体的な圧縮強度です
- fそして 鉄筋降伏強度です
- あg セクションの総面積です
- あst スチール鉄筋の総面積です
- (あg - あst) コンクリートの効果的な断面積です.
この点は、強度還元係数が適用されない相互作用図の左上に対応します. 圧縮制御領域の強度削減係数によってこの値を減らすことができます (私たちは純粋な圧縮であるので、私たちは確かに圧縮制御領域にいます). ACI 318-19 ただし、これを超えて最大制限を課します。.
コンクリート柱の最大許容圧縮能力を計算する方法 (ACI)
偶発的な偏心を説明するため 318-19 鉄筋コンクリートの列の最大許容圧縮容量をに制限します 80 に 85 前のセクションで計算された純粋な公称圧縮能力の割合.
削減は、メンバーのタイプと列で使用される横方向の補強に依存します (テーブルを参照してください 22.4.2.1 ACIの 318-19).
一般的に、横方向の補強が結びついている場所があります:
- Pん,最高 = 0.80 * P0
または、横方向の補強がらせんである場合:
- Pん,最高 = 0.85 * P0
コンクリート柱の純粋な張力容量を計算する方法 (ACI)
鉄筋コンクリートカラムの張力強度は、完全に補強の強さに由来し、私たちが持っている補強の領域に比例します.
鉄筋コンクリート柱の軸方向の張力強度を計算する式は単に:
Pnt,最高 = fそして * あst
&
p1 =φ * Pnt,最高
セクションは純粋な緊張状態であり、私たちのバーはすべて張力が制御され、強度還元係数φは常に張力制御されていると考えられているため 0.9.
コンクリート列のバランスポイント容量を計算する方法
バランスポイントは、極端な張力メンバーが最初にεを生成する原因となる負荷として定義されますt = eタイ コンクリートが生成すると同時に. カラム強度の計算に使用される方法 (屈曲および軸圧縮または張力用) この時点で、特定のεを持つ他のポイントに使用される方法と同じですt (つまり. εt= 0, et = 0.5 εty).
最初にフック法を使用して補強材の降伏ひずみを計算できます:
εty= fそして / E
のために 60 若い弾性率を持つKSIバー 29000 ksiの収量株があります
εty= 60/290000 = 0.00207
また、コンクリートの収量株を常に採用します 0.003 (セクションで定義されています 22.2.2.1 ACIの 318-19).
これらの2つの値を使用して、ひずみダイグラムをプロットでき、ひずみ図に基づいてセクションのストレスを判断できます. 応力の計算は、次の2つのセクションでカバーされています.
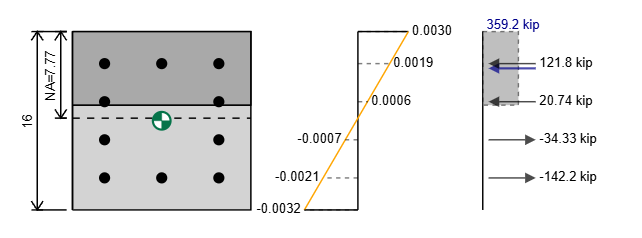
コンクリート柱の補強の力を計算する方法
補強のストレスと力を計算することは、純粋な張力強度の計算方法に似ています. 私たちのストレスは私たちのひずみ時間に等しいですが、私たちのヤング率は私たちの降伏ストレスによって制限されます.
σ= min( et * E , eタイ * E )
その後、この行のバーの領域をストレスに掛けることで、バーの力を決定できます. 同じひずみのある複数のバーがある場合に計算を簡素化するために、これらすべてをグループ化できます.
ft =σ * あ
私たちは、私たちの力が圧縮または緊張状態にあることを区別する方法が必要です. FTとFCを使用してさまざまな力を示すことができますが、この例ではSKYCIV計算機では、緊張を表す否定的な表記と圧縮を表す正の表記表記を使用します。.
コンクリート応力ブロックの力を計算する方法
コンクリートセクションの応力分布は線形ではなく、代わりにほぼ放物線であるため、鉄筋コンクリートカラムのコンクリート成分に対する応力を計算することは、わずかに複雑です. 幸運なことに, ホイットニーストレスブロック法として知られるコンクリートセクションで応力を計算するための経験的単純化が存在します. この方法では、長方形の応力ブロックとして放物線ストレス分布を近似します.
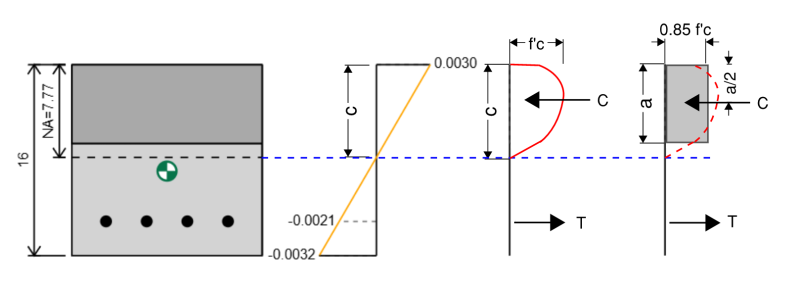
ACIは、この方法についてセクションで説明しています 22.2.2.4.1. ASを計算します:
A = B1 * c
β1の範囲 0.65 に 0.85 圧縮強度に応じて (f'c) コンクリートの (テーブルを参照してください 22.2.2.4.3).
ストレスブロックの力を計算するとき、私たちは常にの効果的な応力を使用します 0.85 * f'c.
そのため、圧縮力を計算できます:
fc = 0.85 * f'c * B1 * c
そして、力は極端な圧縮エッジからA/2の位置で作用します.
ストレスストレイン図からコンクリート列の軸容量を計算する方法
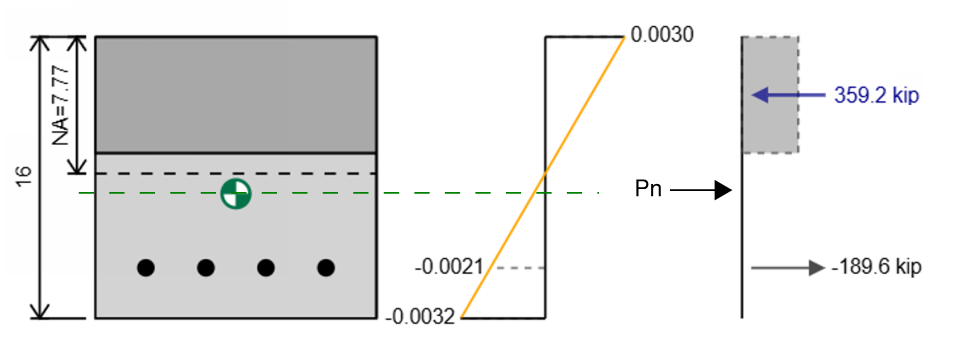
これですべての株があります, 私たちのセクションでは、補強とコンクリートにストレスと力がありますが、このセクションの軸方向容量または曲げ能力はまだ特定されていません。.
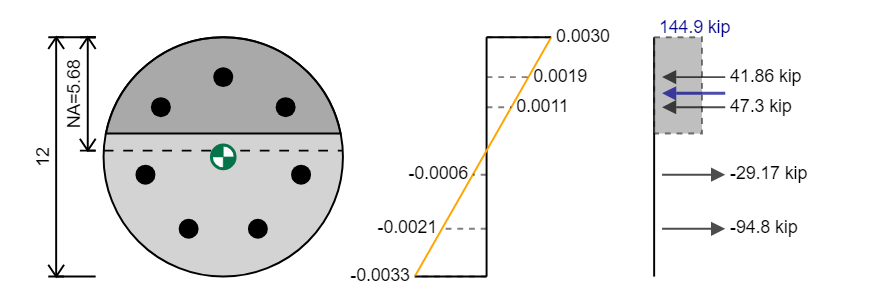
軸方向の容量は結果の力であり、それが作用する位置はプラスチック重心です (図の緑の重心マーカー). 上記の例では、軸容量はです
原則を使用しますstaticsのlesフォース図を使用して、セクションの能力を決定できます. まず、力の合計を使用して軸方向の容量を決定できます, 私たちの総圧縮力は、私たちの総張力と等しいことを知っているセス.
σfx= 0 →σc=σt
その後、鋼の圧縮力とコンクリート圧縮力と鋼の張力を合計して、セクションの軸容量である結果の力を見つけることができます.
pn =σc - σt
たとえば、持っている場合 359.2 圧縮のキップと 189.6 緊張のキップ セクションの場合、結果の力は次のとおりです 359.2 - 189.6 = 169.6 キップ. セクションのバランスを完全にバランスさせる力が描かれていることに注意してください (つまり、の張力 169.6) 容量の反対です 169.6 できるので圧縮のキップ
ストレスストレイン図からコンクリート柱の曲げ能力を計算する方法
私たちは今、それのバランスをとるために私たちのセクションに作用する力が必要であることを知っています. この力は、上の図面の緑の重心マーカーによってマークされたセクションのプラスチック重心に作用します.
プラスチック重心を見つけるために、計算は 通常の重心計算 Aを距離で掛ける代わりに、私たちは距離を複数増やす.
曲げ能力を計算するために、あらゆる位置について瞬間をとることができ、純瞬間を獲得します. プラスチック重心の位置についての瞬間をとることができますので、レバーはそのレバーになるので、計算で力PNを心配する必要はありません 0. テーブルは、特に補強の層がたくさんある場合、これらの計算に役立ちます.

私たちの瞬間の容量の計算は
mn = σfx lever = 359.2 バツ 5.615/12 + -189.6 バツ -4.206/12 = 168.1 + 66.5 = 234.6 キップフィート
正の瞬間は、セクションの上部が圧縮されており、セクションの下部が緊張していることを意味します.
コンクリート柱の還元能力と軸容量を計算する方法
の瞬間容量を計算しました 234.6 KIP-FTとの圧縮能力 169.6 しかし、これらは私たちの究極の能力であり、強度削減係数PHIによって減らす必要があります.
現在、バランスポイントを検討しており、εt=εtyを持っているため、圧縮制御領域にいて、 0.65 または 0.75 鉄筋コンクリート柱の横方向の補強に応じて.
相互作用図のプロット
これまでのところ、計算方法を見てきました
- (P1) 純粋な張力ポイント
- (p6) 純粋な圧縮点
- (P3) バランスポイント
バランスポイントの計算と同じ手順を使用して、軸方向と曲げ能力を計算することもできます:
- (P4) ハーフイールドポイント
- (p5) 減圧点
これら3つのポイントの違い (p3、p4、p5) 同じものに続いて、すべてのステップでひずみ図を生成する際に行う最初の仮定です.
これらの5つのポイントが決定されたことで、計算していない唯一のポイントは純粋な曲げポイントです. この点は、pn =を持っているポイントに対応しています 0 私たちのセクションで. この点を決定するには、中性軸の位置を推測する反復ソリューションが必要です (ACIのCの値) pn =かどうかを判断します 0. 中性軸のこの位置を見つけたら、バランスポイントで行ったようにステップを続けることができます.
すべての値が決定されると、鉄筋コンクリート列の相互作用図を生成できます. キーポイントを描画し、それらの間に直線をプロットして、簡単な相互作用図を作成できます. Skyciv Quick Design Concrete Columnのようなソフトウェアを使用する.
ACIに設計するときにプロットするのに役立つ可能性のある別のポイント 318-19 圧縮制御遷移点である位置P3で行うように、PHI因子が変化し始める場所であるため、張力制御遷移点は張力です。. また、最大許可された純粋な圧縮力が減少しているためにも注意してください (青い線で示されます) 最大圧縮力は、以下のグラフでポイントP6で示されるモーメント容量に抵抗することもできます.
相互作用図を読む方法?
これまでのところ、相互作用図を作成する方法について多くのことを学びましたが、どのようにデザインでそれを使用することができ、なぜそれが必要なのですか.
最終的に, 相互作用図は、私たちのセクションで常に同じであるため有用です (特定の方向に曲がるとき) そして、私たちの軸方向の力と瞬間のバリエーションに依存していません.
セクションに単一の軸力とモーメントの組み合わせの容量がある場合にのみ計算する場合にのみ、図は必要ないかもしれませんが、考慮したい複数の異なる負荷の組み合わせと力がある場合、非常に反復的な計算になります。.
相互作用図は、ACIなど、特定の負荷の組み合わせが設計基準の要件を満たしているかどうかを迅速に判断できる視覚ツールを使用して使用します。 318-19. 私たちがする必要があるのは、私たちのポイントをプロットし、それが私たちの相互作用図の領域内にあることを確認することです, そして、私たちは多くの異なる負荷の組み合わせをすべて同時にプロットすることができます.
私たちが主にこの地域にいるかどうかに関心があるため、利用率はわずかにarbitrary意的です, ただし、特定の境界からどこまでであるかによって、使用率を定義できます. x軸の距離は、相互作用図の瞬間の利用であり、y軸の距離は相互作用図の軸の利用です.
コンクリート柱に二軸曲げのための相互作用図を作成する方法
私たちが以前に見た相互作用図は、長方形の鉄筋コンクリートセクションの一軸曲げのためのものでした. 私たちは、曲げが1つの軸について起こっているとしか考えていませんが、マイナー軸曲げもすることもできます. マイナー軸曲げの場合、セクションを回転させることを除いてすべてを実行します 90 学位を持っているので、代わりにこのようなものがあります.
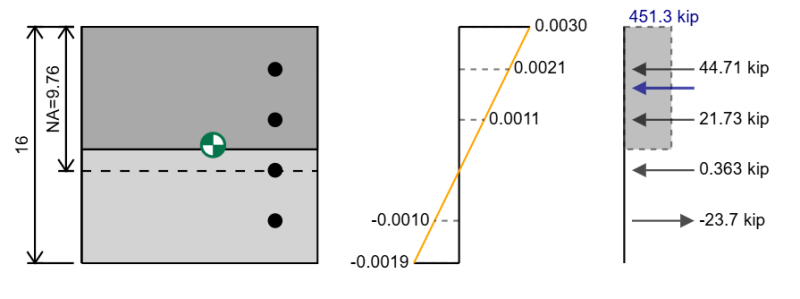
二軸曲げには、結果の瞬間の平面の周りに曲がっているので、セクションを回転させる必要があります. この二軸図に得られる相互作用図は、結果として生じるこの特定の方向にのみ関連しています.
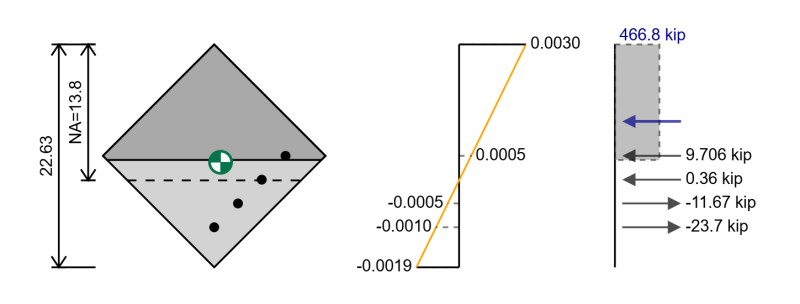
以前の相互作用図で行ったのと同じ手順に従うことができます。これを除いて、補強のための異なる位置があり、二軸曲げの長方形のセクションの場合、圧縮中の三角領域があります。.
コンクリート圧縮力を計算する代わりに:
fc = 0.85 * f'c * B1 * c
代わりに、コンクリート圧縮力を計算できます:
fc = 0.85 * f'c * あ
ここで、Aは位置A =β1の上の圧縮の領域です * c
3D相互作用図とは何ですか?
二軸曲げの2D相互作用図を作成することの制限の1つは、特定の結果のモーメント方向にのみ関連することです。. 私たちの能力を考慮する際に3つの変数があります。なぜMZがあるのですか, 私とn. 当然、2つの軸のみを処理できるため、2つの変数を処理できる2Dチャートを使用する代わりに、3つの変数を処理できる3次元相互作用図を作成できます。.
2D相互作用図のように、私たちの目的は、チャートの領域内に負荷の組み合わせを置くことです。今では考慮すべき3つのポイントがあることです。 (Mz, ぼくの,N) そして、私たちのポイントは、相互作用図のボリュームに含める必要があります (エリアではなく). これは、複数のポイントを同時に評価するための有用な視覚ツールですが、その制限は、静的グラフや画像などの2Dメディアで使用することが困難であり、このようなグラフを完全に利用するためにインタラクティブなソフトウェアが必要であることです。. SkyCIVセクションビルダーは、作業が簡単な3D相互作用図の生成に役立ちます.
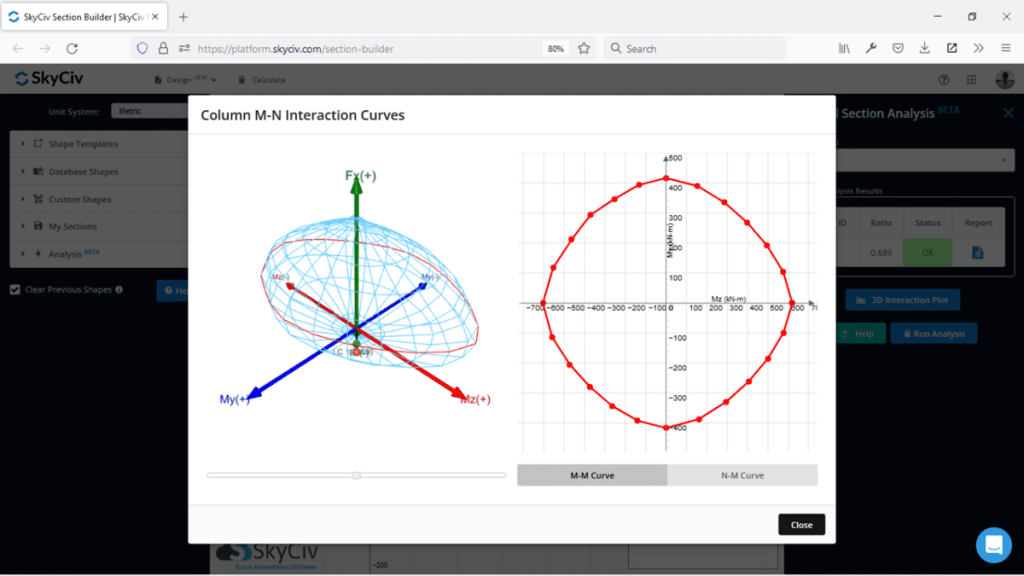
3D相互作用図を作成する方法
すべてのデータポイントを取得するには、3D相互作用図を作成するために必要な3D相互作用図を作成するために、以前と同じ2D評価を行います。. 好きな回転を使用できます, 合理的な角度がある可能性があります 15 私たちに与えてくれる学位 24 異なる角度.
データを手作業で取得することは退屈ですが可能ですが、そのデータを使用して3Dインタラクティブな相互作用図を作成することは非常に困難です. 3D相互作用図は、SkyCIVセクションビルダーのようなソフトウェアで使用するのが最適です.
関連ツール
SkyCivについて
SkyCivは、エンジニアに幅広いCloud Structural Analysis and Design Softwareを提供しています. 常に進化するテクノロジー企業として, 私たちは、既存のワークフローの革新と挑戦に取り組み、エンジニアの作業プロセスと設計の時間を節約します.