モーメント分布法手計算

SkyCivでは、教育が重要であると考えているため、次世代のエンジニアが構造工学を学ぶのを支援することに取り組んでいます。. このミッションの一環として, 私たちは構造工学ソフトウェアのブラックボックスを開くモーメント分布法手計算レポートを開発してきました。, ユーザーの好奇心にさらされる. エンジニアは、何かがどのように、そしてなぜそのようになっているのかを知りたがっています, そして 多くの場合、これを学ぶための最良の方法は、自分で解決して、完全で正しいソリューションと比較することです。. レポートの読みやすさと、計算のバックチェックに必要な詳細レベルのバランスをとります, 一歩一歩. これはエンジニアリングの実践の基本であり、今後もユーザーに教育に付加価値を与えるツールを提供します, 仕事, そして生きています.

私たちはあなたが望むものによって動かされます: ユーザーから最も要望の多かった機能の1つは、不確定ビームの手計算でした。. この機能が公開されたことをお知らせします: 現在の学生, ベーシックユーザーとプロフェッショナルユーザーはやってみよう. ヒンジのない不確定な梁の場合, 垂直およびモーメント反応は、モーメント分布法を使用して解決されます.

モーメント分布法手計算モジュール, 次のようなビームの手の計算を簡単に表示します:

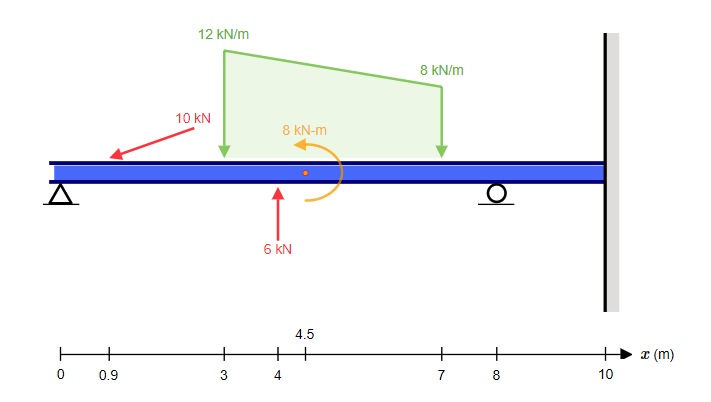
ただし、既存のユーザーは、Beamの静的に決定された構造の手計算へのアクセスに精通しています。, SkyCivを初めて使用する場合、または見つけた手の計算をまだ試したことがない場合, 私たちのドキュメンテーションプロセスをご案内します.

今日それを試してください!

モーメント分布法

モーメント分布法 (MDM), ハーディクロスによって発明されました, シンプルさの点で非常に強力であり、ASCEジャーナルによって最初に発行されて以来広く使用されています。 1930. その単純さの一部は、各セグメントの不連続方程式を計算する必要なしに、重ね合わせを使用して曲げモーメント図をグラフィカルに描画できる方法にあります。. 複雑な構造は、FEMなどの他の方法と比較して比較的簡単に解決できます, 仮想変位法, または不連続方程式を解く. MDMは、梁やフレームなどのさまざまな2D構造で使用できます。.

ハーディクロスは、手計算が構造エンジニアにとって不可欠な演習であった時代の構造エンジニアでした. 構造を計算するプロセスを数え切れないほど繰り返した後、彼は本質的に同じ計算を何度も何度も完了していることに気づきました。. これにより、Crossは、複雑な構造は実際には単純な構造と, これらの単純な構造を組み立てて、同じ分析ソリューションで複雑な構造を作成することができます. 単純な構造は簡単に解決できます, 数式は、たとえ不確定であっても、簡単に導き出すことができました。, 重ね合わせと仮想力法のおかげで. クロスはこれらの単純な構造のテーブルを作成し、さまざまな方法で彼の理論をテストしました.

固定端モーメント方程式

モーメント分布法では、一般的な荷重ケースの表を使用して、各セグメントの端のモーメントの方程式を検索します。. これらの表は、次のドキュメントに記載されています。曲げモーメント図の計算 MDMが使用される基礎を形成するだけではありません, だけでなく、単純な曲げモーメントの計算のための優れたリファレンスです. それを見る簡単な方法は, MDMはビームをセグメントに分割します, これらの簡単な方程式を使用してBMDを計算します.