Sections asymétriques
Les sections asymétriques ne sont pas symétriques dans l'axe des y vertical ou l'axe des z horizontal ou, dans certains cas, n'importe quel axe. Des exemples de sections asymétriques sont les angles et les sections en Z.
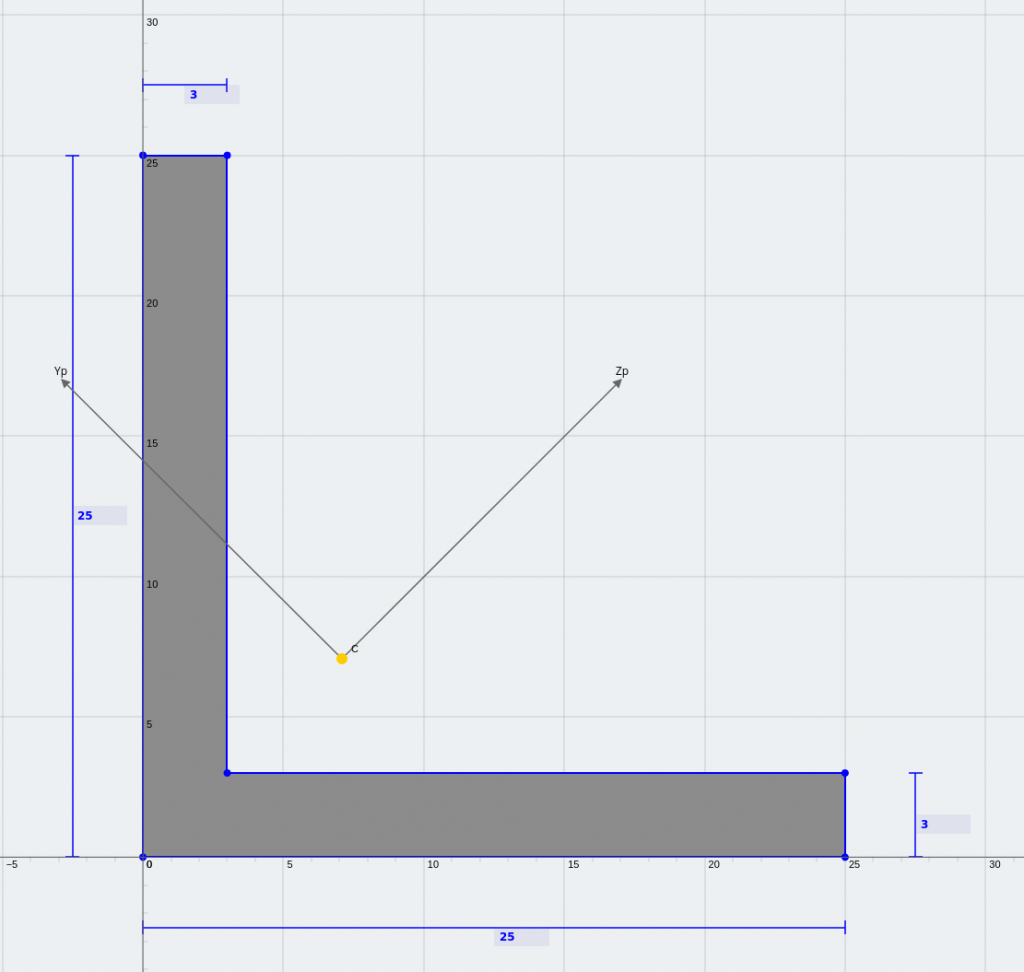
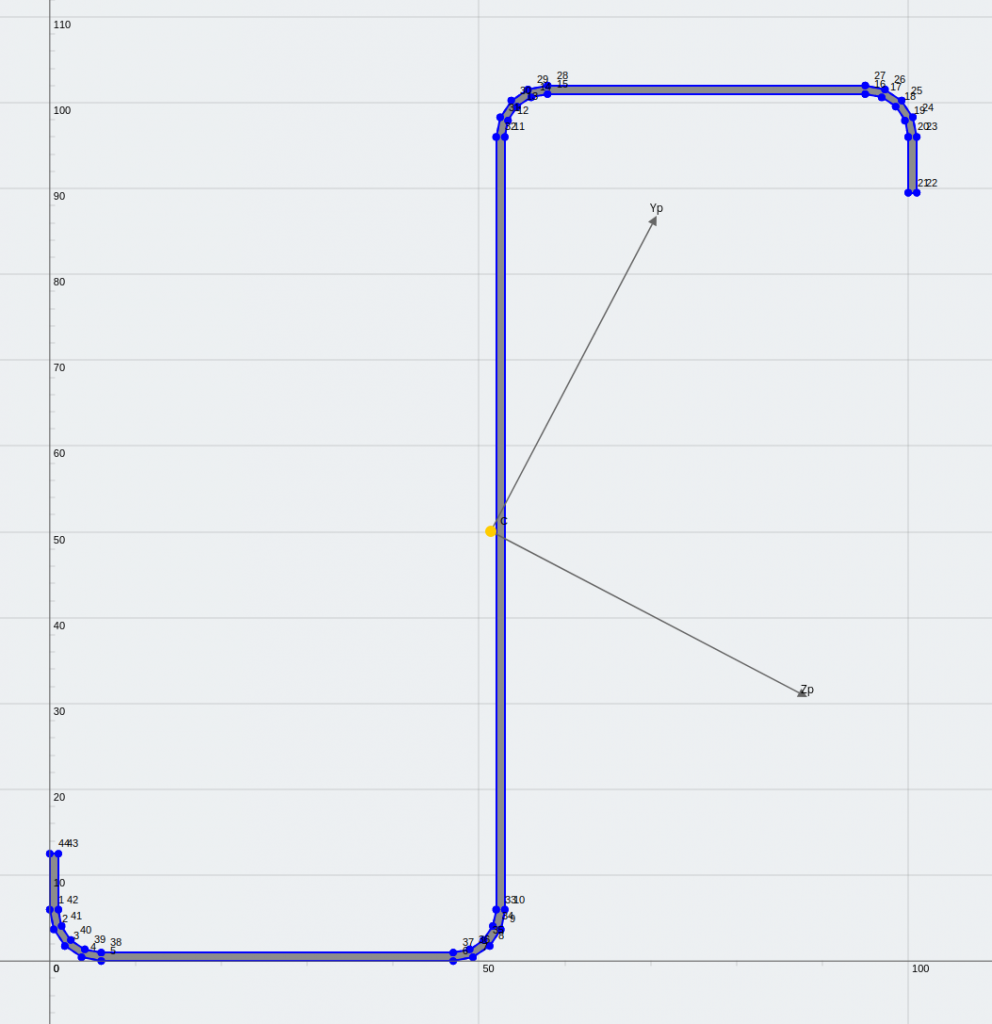
Une section à angle égal (Une section à angle égal)
Les poutres à sections asymétriques se comportent différemment des poutres à bi-symétrie en flexion. Même si la poutre a une rigidité équivalente dans l'axe vertical, elle ne se comportera pas comme un RHS et I Shape le fait.
Dans cet exemple, je vais démontrer leur comportement avec un cas de charge simple: une charge verticale uniformément répartie.
Analyse
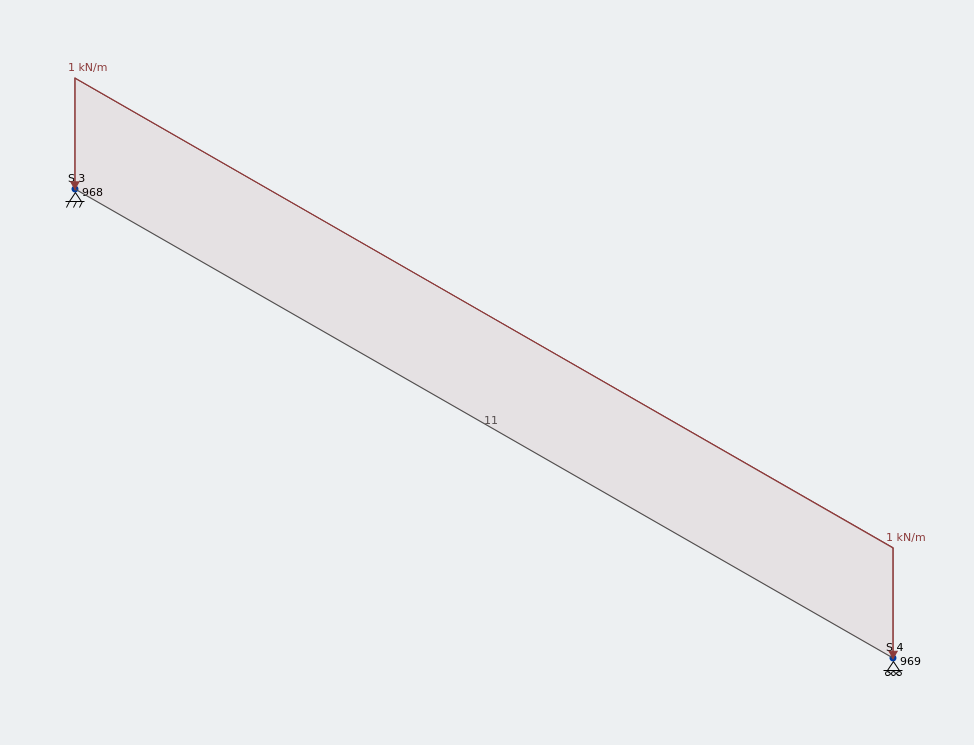
Modèle de cadre d'un 1.5 m angle égal sous UDL vertical
J'ai appliqué une charge uniformément répartie de 1 kN/m sur toute la longueur de ce 1.5 m angle égal.
Si je voulais vérifier la déflexion à mi-portée de cette poutre, je pourrais assez facilement. Tout ce dont j'aurais besoin serait le deuxième moment de la zone, et la formule de déflexion maximale standard pour une poutre simplement supportée. Un calcul rapide à l'aide de SkyCiv Section Builder et j'obtiens facilement les propriétés de la section.
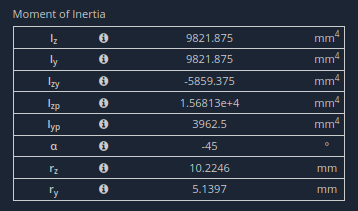
Propriétés de la section tabulée de SkyCiv Section Builder
Iz est 9821.9 mm à la puissance 4. La section est en acier de construction avec E = 200 GPa.

Regardez ce qui se passe lorsque je calcule cela avec FEA dans SkyCiv Structural 3D.
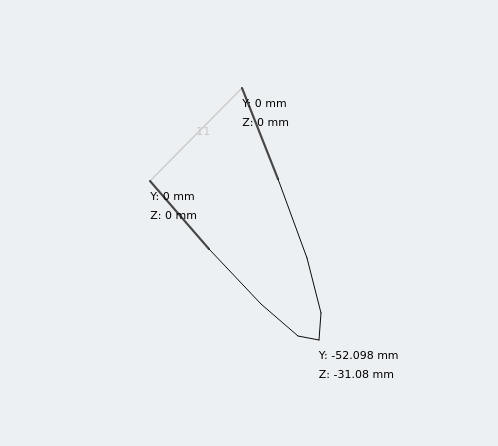
Déplacement d'angle égal sous charge
La section à angle égal a deux composantes de déviation! Analyser la flèche d'une poutre simplement appuyée à l'aide d'une section bi-symétrique en utilisant le calcul précédent, ce serait une approche parfaitement acceptable pour un contrôle rapide. Mais pour les sections asymétriques, nous avons besoin d'une autre information.
L'angle
Notez que dans les propriétés de la section ci-dessus, la valeur de est non nulle.
Cela signifie que l'axe principal n'est pas parallèle à l'un des axes géométriques.
Démontrer l'effet de la rotation de l'axe sur les valeurs de rigidité calculées, J'ai tracé ci-dessous la rigidité dans l'axe horizontal et vertical lorsque le système de coordonnées est tourné.
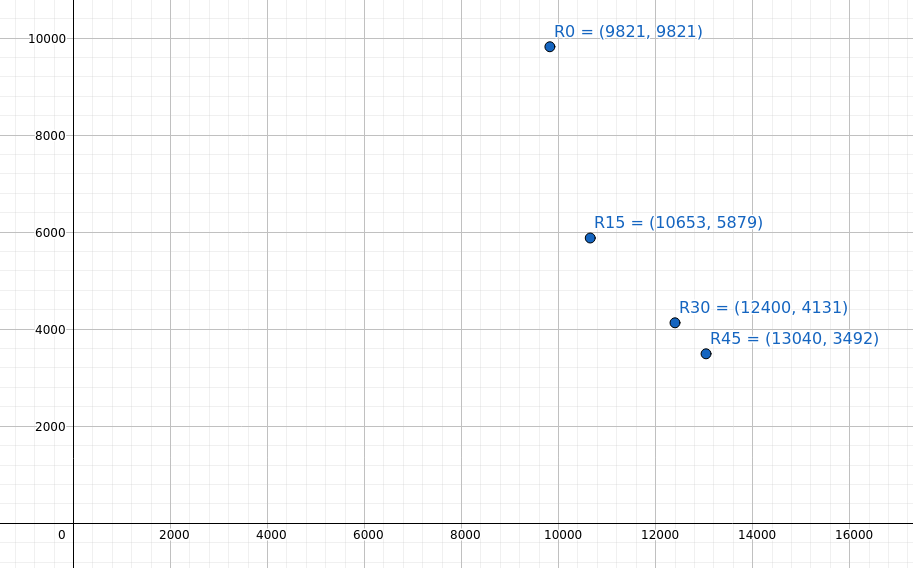
Rigidité de 25x25x3 EA après rotation du système de coordonnées
Notez la courbe non linéaire qui se forme lorsque le système de coordonnées tourne à travers 15, 30 et 45 degrés. Cette courbe sera unique à la section.
Pourquoi cela se produit-il donc?
Un conférencier m'a dit une fois que les charges suivent les parties les plus rigides de la structure. Dans le cas présent, la charge est portée par l'axe le plus rigide (le grand axe principal).
La bonne approche
La bonne façon de calculer les résultats de déflexion consiste à transformer d'abord toutes les charges dans les axes principaux, puis calcul des déflexions sur la base du deuxième moment de surface le long des axes principaux. Pour prouver que c'est bien la bonne approche, j'ai validé la réponse à l'aide d'un calcul manuel, et pour rendre cela un peu plus intéressant, avec un modèle de la poutre à l'aide d'un élément de cadre et, un modèle construit à partir de coquillages. De cette façon, il ne fait aucun doute que les déplacements que nous avons vus avant sont en effet corrects.
Voici le modèle que j'ai créé.
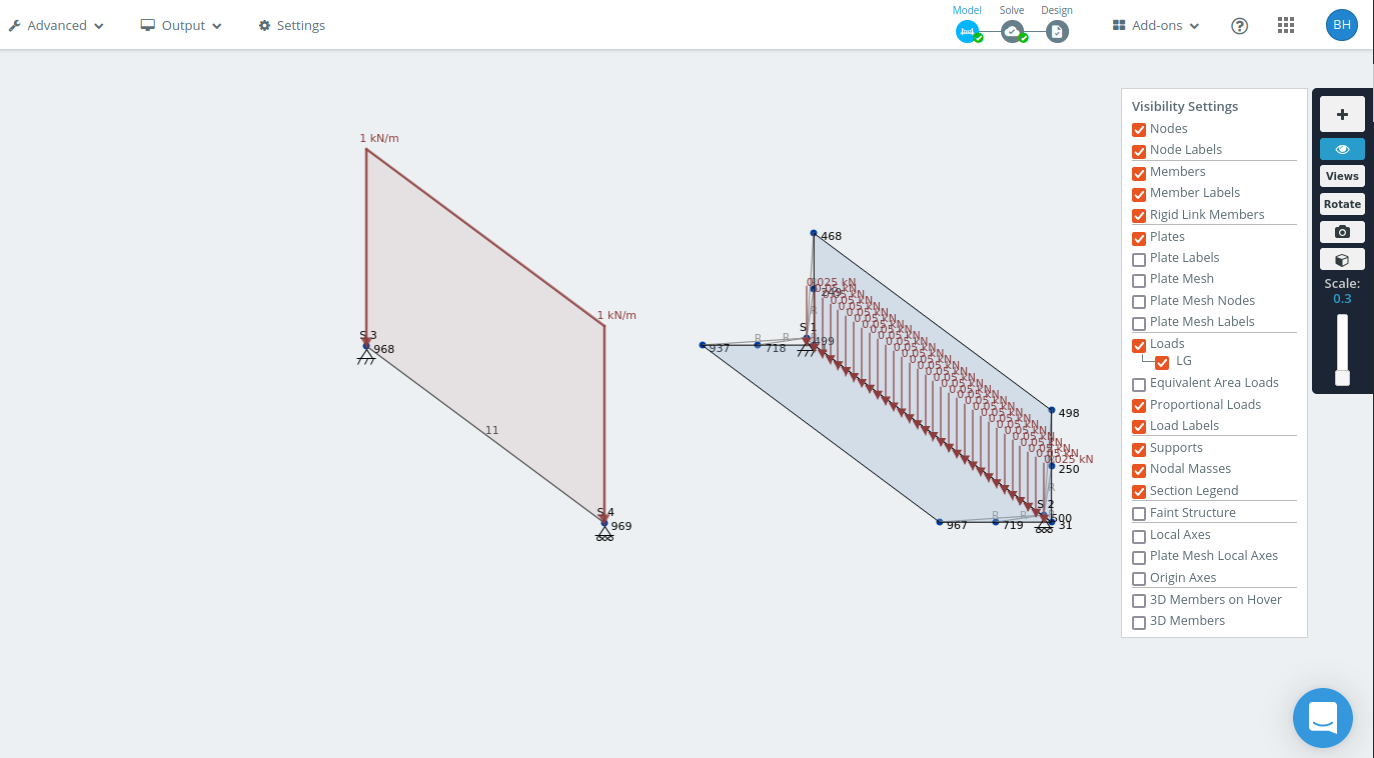
Modèle de cadre et modèle de coque de 1.5 m angle
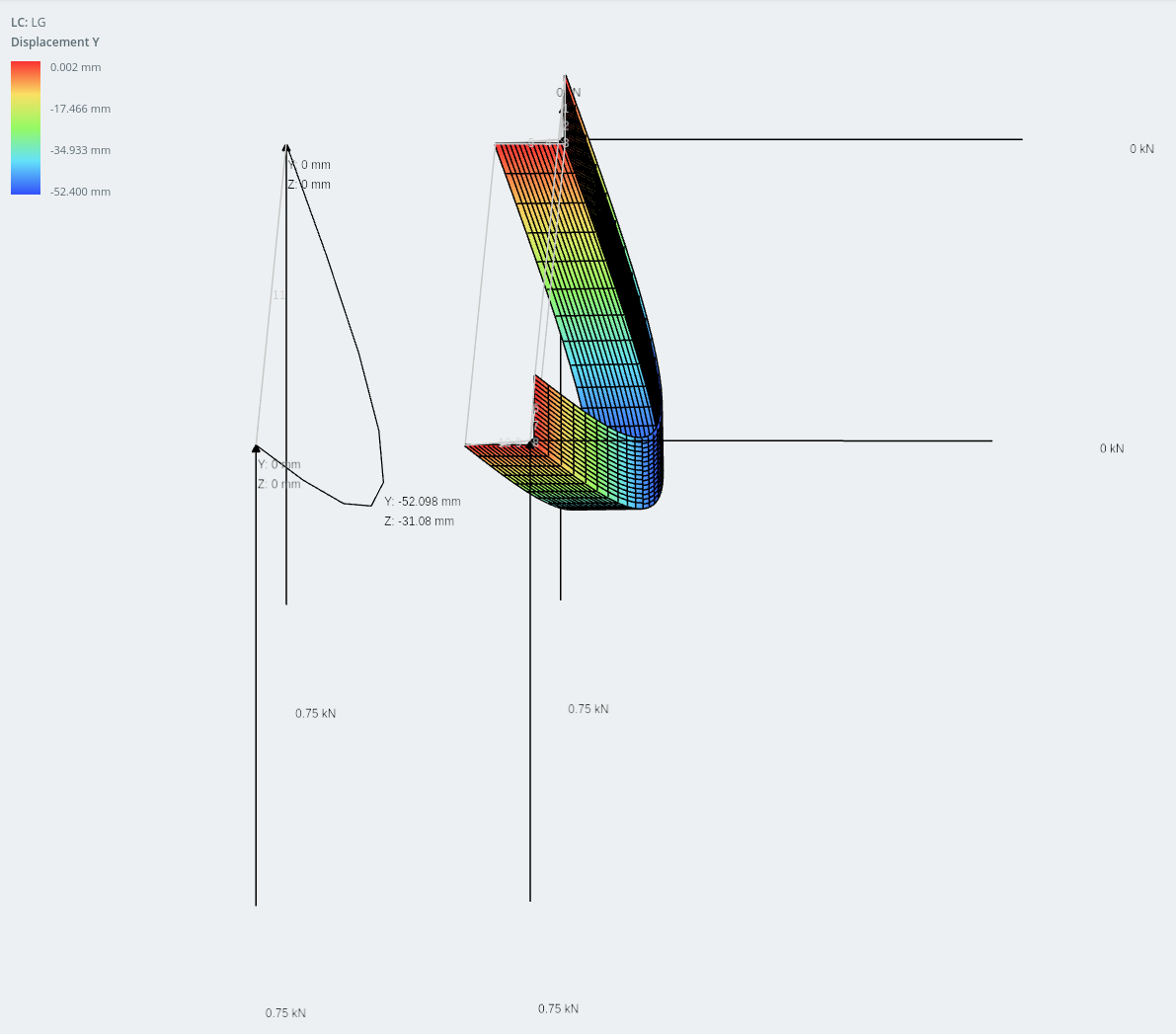
Déplacement dans le sens vertical
La différence de résultats entre les deux modèles est extrêmement proche: dans 1% l'un de l'autre.
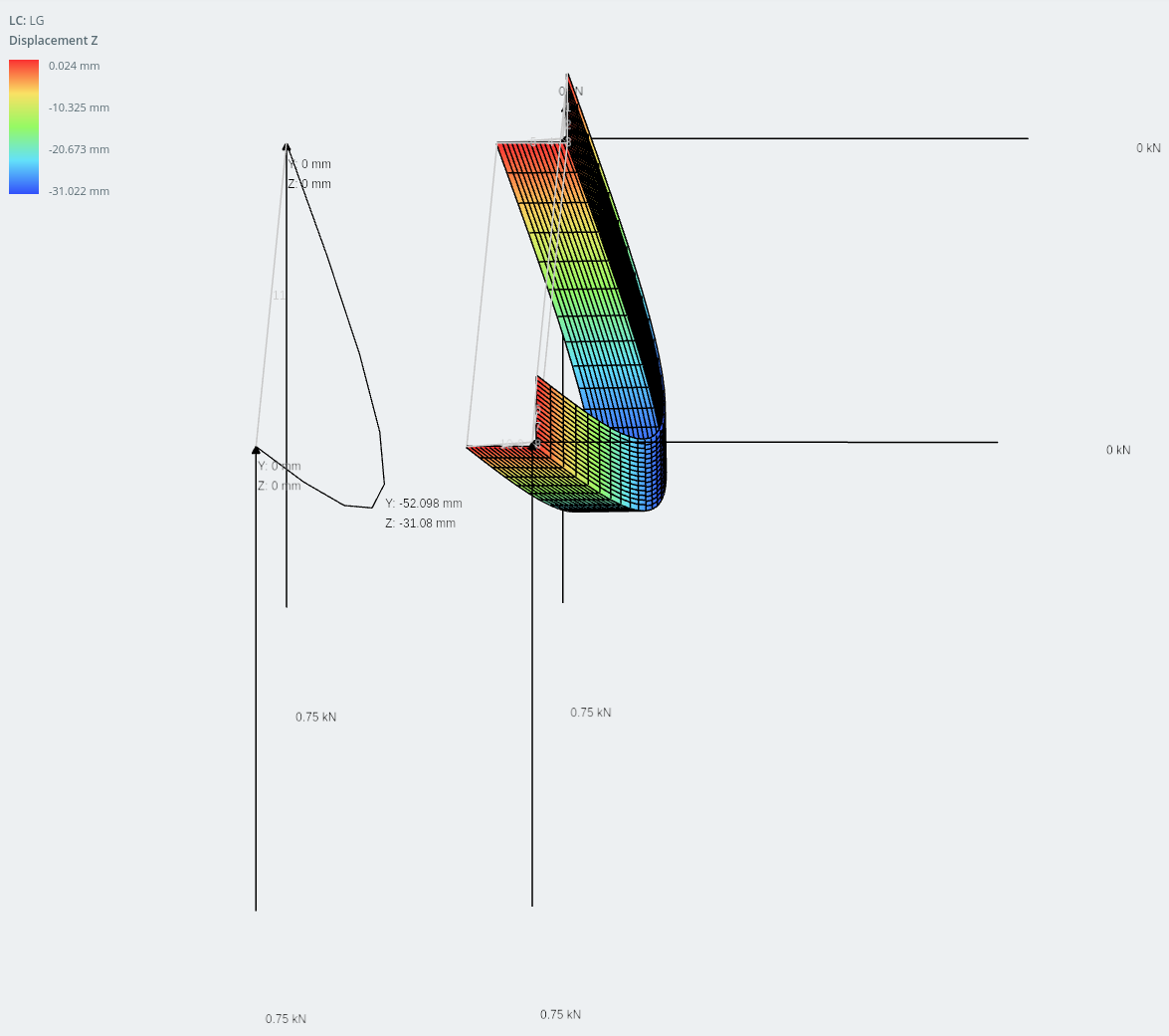
Déplacement dans le sens horizontal.
Et ils sont confirmés par les calculs manuels ci-dessous.

Pourquoi voudriez-vous utiliser ces sections?
L'ingénieur aime concevoir des structures légères et efficaces, cependant parfois il y a des limitations sur la forme des composants structurels, généralement en raison de décisions de conception prises par d'autres. Cette contrainte de forme peut être due à de nombreuses raisons, c'est peut-être parce qu'un architecte veut cacher des éléments structurels pour des raisons esthétiques, ou pour se conformer aux lois d'urbanisme locales. Il se peut qu'il y ait des limitations dues à la capacité de fabrication locale ou simplement à la disponibilité et au coût des matières premières. Les coûts de fabrication et le revêtement peuvent également jouer un rôle important. quelquefois, nous sommes coincés avec ce que nous avons.
Quand il y a le choix, la section peut être choisie car elle présente certains avantages. Prenons par exemple les sections Z, que l'on voit couramment supporter des tôles d'acier profilées inclinées. Typiquement pour les petits angles de toit inclinés, les canaux sont plus efficaces car les charges de gravité ne causent que de minuscules moments autour de l'axe faible. Ces moments augmentent à mesure que l'inclinaison du toit augmente et à une certaine inclinaison, Les sections Z deviennent plus efficaces.
Pour démontrer, j'ai modélisé la section lèvre-Z comme une poutre en acier de 1,5 m. Une section à angle égal.
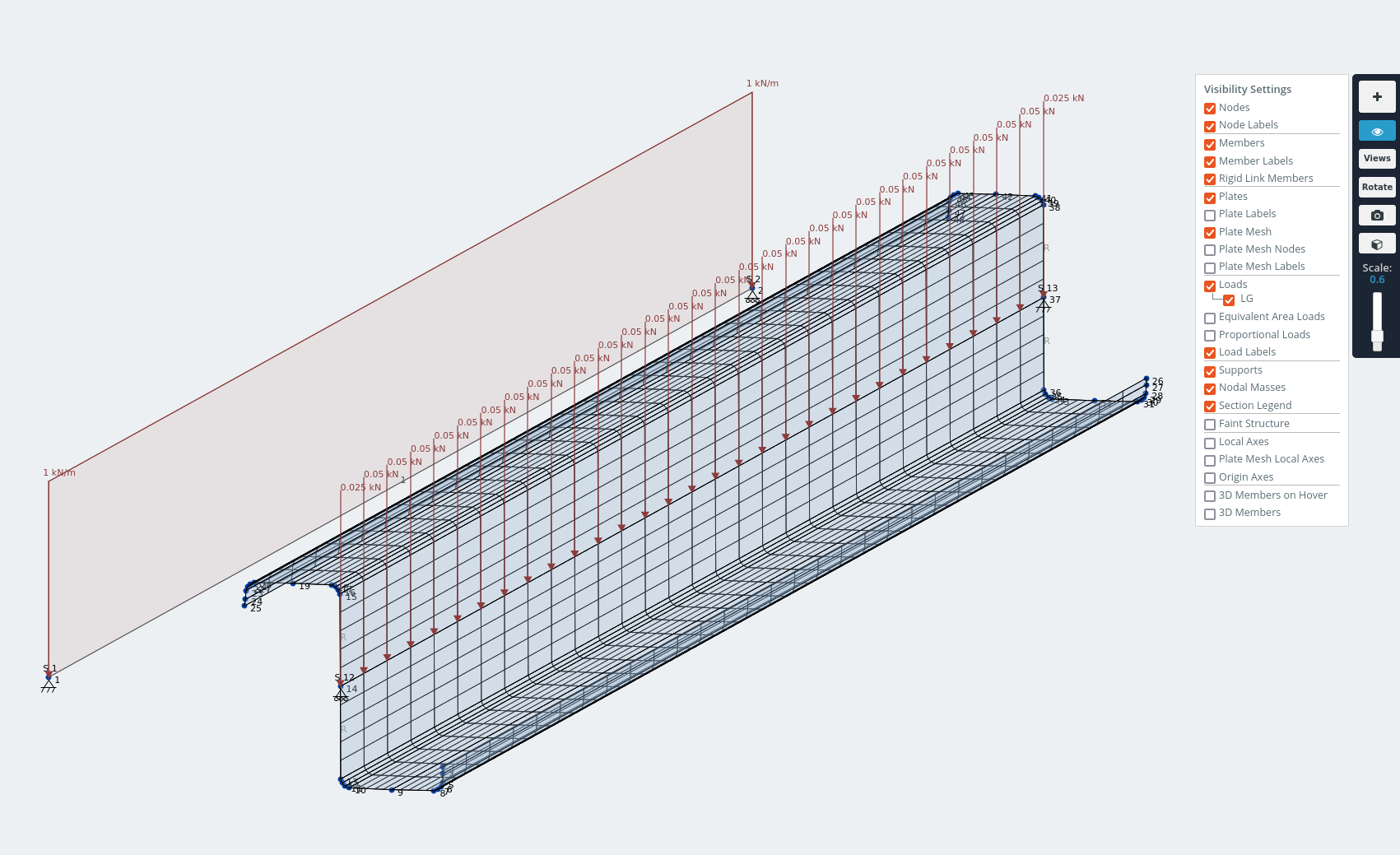
Modèle de section à lèvres en Z avec une charge répartie de 1 kN/m appliquée par le centre de cisaillement.
Le déplacement dans l'axe z s'oppose à l'action de cisaillement dans le plan de la tôle du toit sous les charges de gravité.
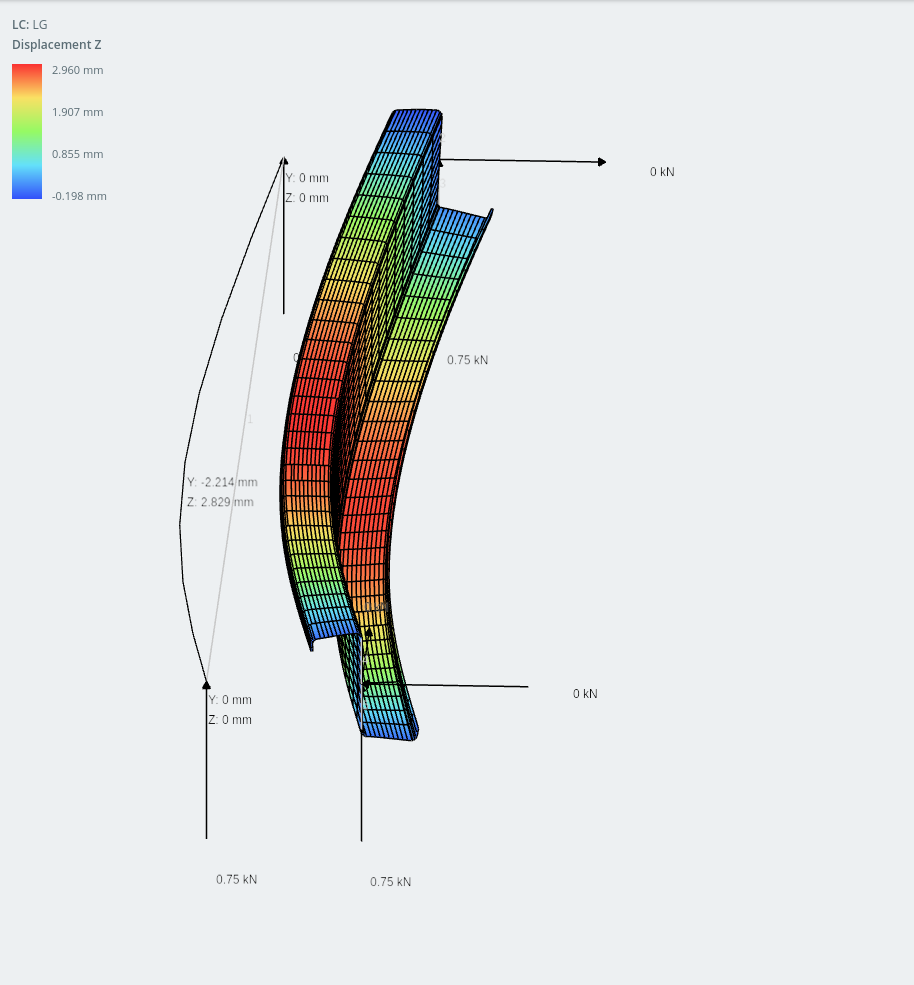
modèle de cadre à section en Z et modèle de coque (déplacement horizontal indiqué sur les plaques)
Étonnamment, le déplacement dans l'axe des y (vertical) est en fait inférieur à l'horizontale. Une section à angle égal, Une section à angle égal, Une section à angle égal, Une section à angle égal!
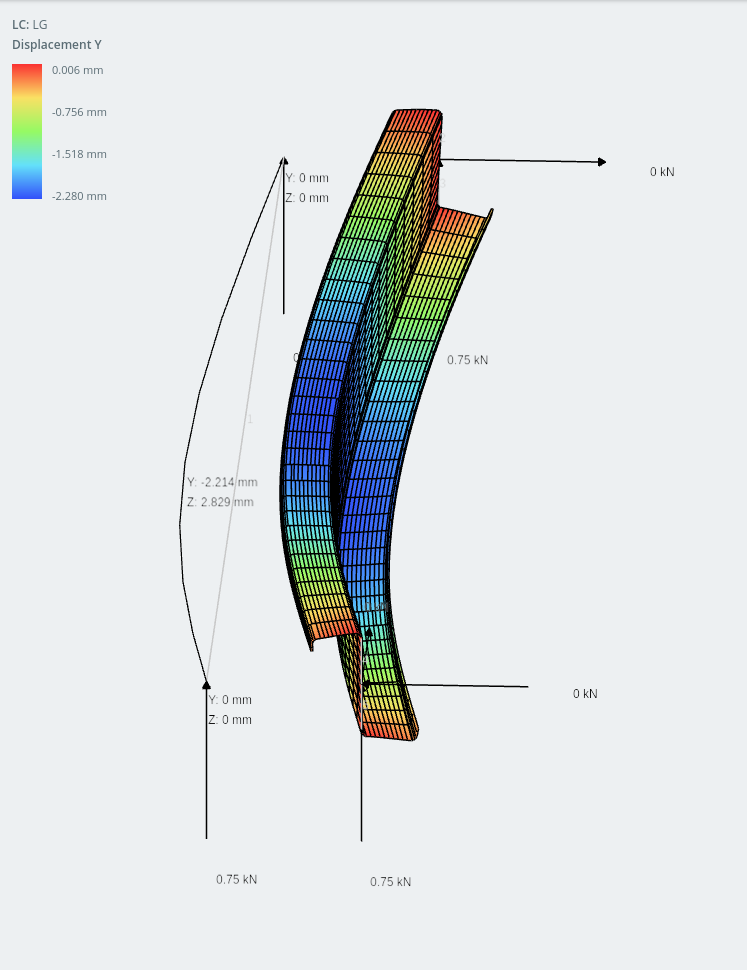
section lèvres-Z (déplacement vertical indiqué)
Une section à angle égal. Une section à angle égal?
J'espère que vous avez trouvé ce post intéressant, si vous avez des questions ou des commentaires sur les sections asymétriques, ou si vous souhaitez voir plus de contenu comme celui-ci, veuillez laisser un commentaire ci-dessous.


