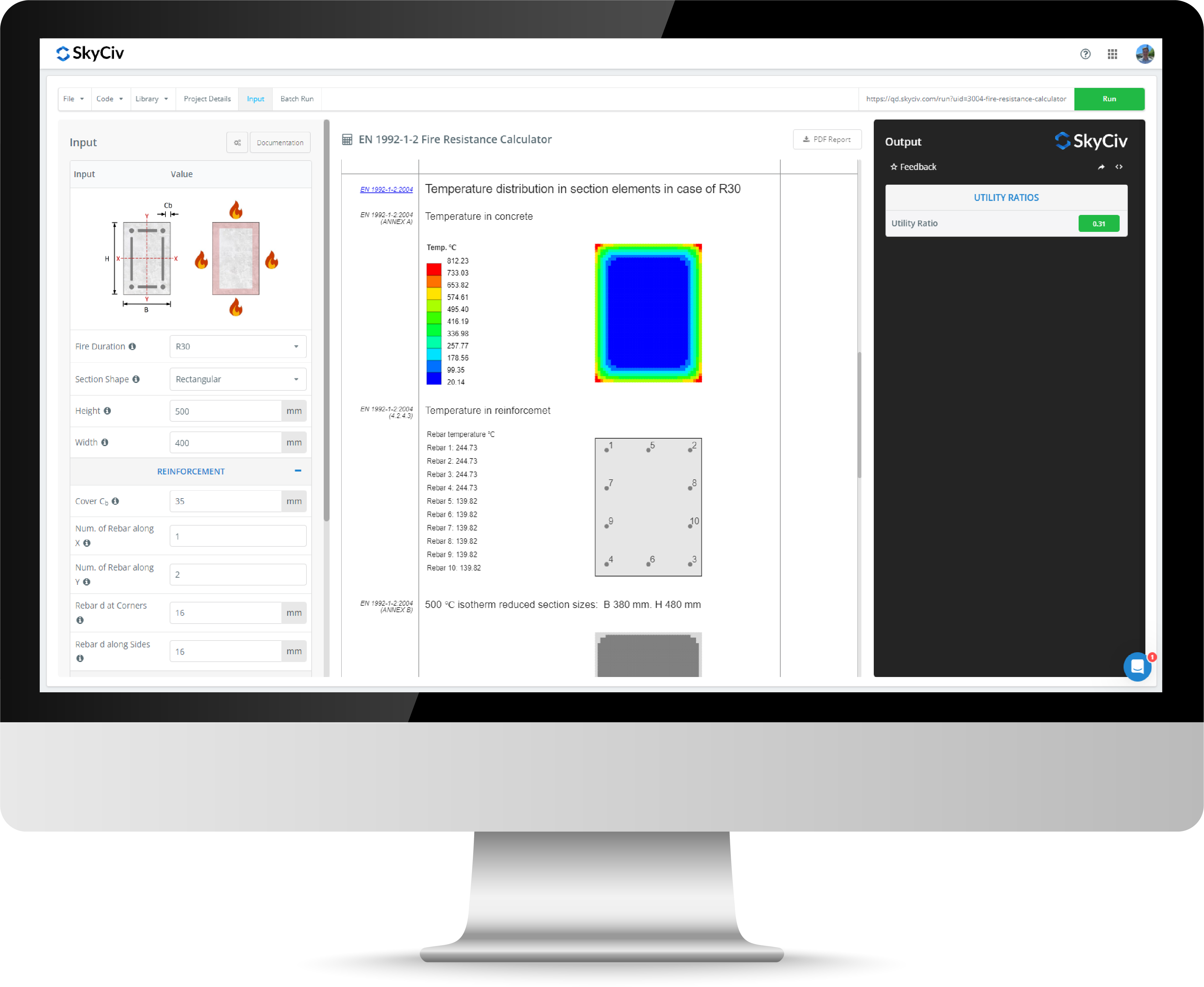
Calculatrice de conception de colonne en béton armé
La calculatrice de colonne en béton armé skyciv permet aux ingénieurs de terminer la conception de colonne en béton armé pour les colonnes en béton circulaire et rectangulaire en ACI, européennes, et normes australiennes. Les colonnes en béton armé sont une section composite qui combine les avantages du béton et de l'acier de manière économique. La nature composite d'une colonne en béton armé rend les calculs de conception plus rigoureux que les autres sections et la calculatrice de colonne de béton rapide fournit un outil facile pour les ingénieurs pour évaluer les capacités et générer des diagrammes d'interaction pour les normes suivantes:
- des États-Unis - ACI-318-19: Exigences du Code du Bâtiment pour le Béton Armé.
- Normes australiennes - AS 3600-2018: Structures en Béton, Acier & Tendons.
- Normes européennes - Eurocode 2: Conception de structures en béton (EN 1992-1-1:2004).
- Normes néo-zélandaises - NZS 3101:2006: La conception des structures en béton
Vous pouvez basculer entre ces normes dans le en haut à droite de la calculatrice en béton en utilisant l'icône de drapeau trouvé en haut du panneau d'entrée du côté gauche. Pour exécuter la calculatrice, appuyez sur le bouton Exécuter en haut à droite du logiciel.
À propos de la conception de colonne de béton
Que sont les colonnes?
Les colonnes sont des membres verticaux dans un bâtiment et sont essentiels pour permettre à la charge dans un bâtiment de se déplacer vers sa fondation. En tant que membres verticaux, Ils traitent principalement des grandes charges de compression en raison des forces de gravité, mais naturellement en raison des excentricités de chargement et des forces latérales telles que les charges de vent et de tremblement de terre, elles sont également nécessaires pour résister aux moments de flexion. Les colonnes sont assez similaires aux piles, sauf que les piles ont du sol pour aider à se limiter à le flambement et peuvent résoudre les forces le long de la tige du tas où en tant que colonne résiste aux forces à sa base. Les piles ont presque toujours une section circulaire, mais les colonnes en béton ont généralement des sections transversales circulaires ou rectangulaires.
Pourquoi utiliser des colonnes en béton?
Les colonnes sont exposées à de grandes forces de compression qui nous donnent naturellement envie d'utiliser du béton, Une solution très économique pour faire face aux charges de compression. Malheureusement, Le béton ordinaire est cassant et faible en tension et en flexion, il est dangereux d'utiliser sans barres d'armature en acier (barre d'armature).
Les colonnes en béton armé utilisent la résistance à la compression du béton et la résistance à la tension des barres d'armature pour une conception de colonne économique. Les colonnes en béton sont largement utilisées dans la construction en raison de leur durabilité, résistance au feu, et capacité à soutenir des charges lourdes.
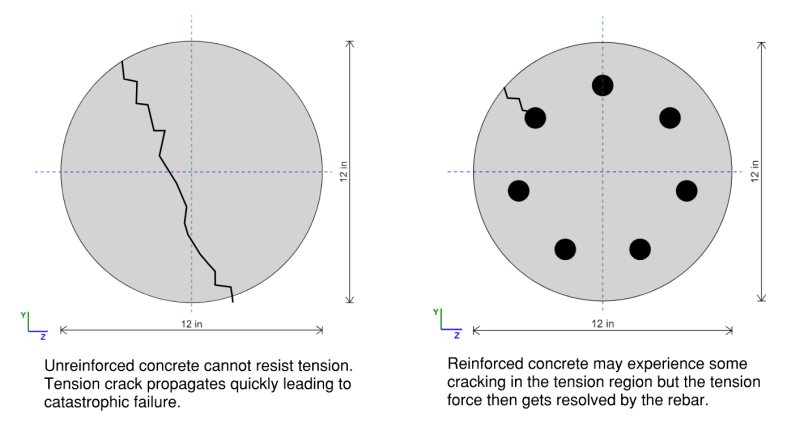
Comment concevoir des colonnes en béton armé
La nature composite d'une colonne renforcée rend plus difficile l'analyse des premiers principes. Avec l'acier, nous pouvons simplement calculer le module de section et multiplier cela par la limite d'élasticité pour trouver une capacité de flexion. Avec le béton armé, la section n'est pas homogène et avec deux matériaux différents, nous devons examiner le graphique contrainte-déformation pour vraiment voir ce qui se passe et comment notre section pourrait échouer.
Cela devient plus difficile lorsque nous considérons que les colonnes ont presque toujours des forces de flexion et de compression agissant simultanément, ce qui affecte la capacité de la colonne. Un outil pour aider à une telle conception est ce que l'on appelle un diagramme d'interaction.
Qu'est-ce qu'un diagramme d'interaction ?
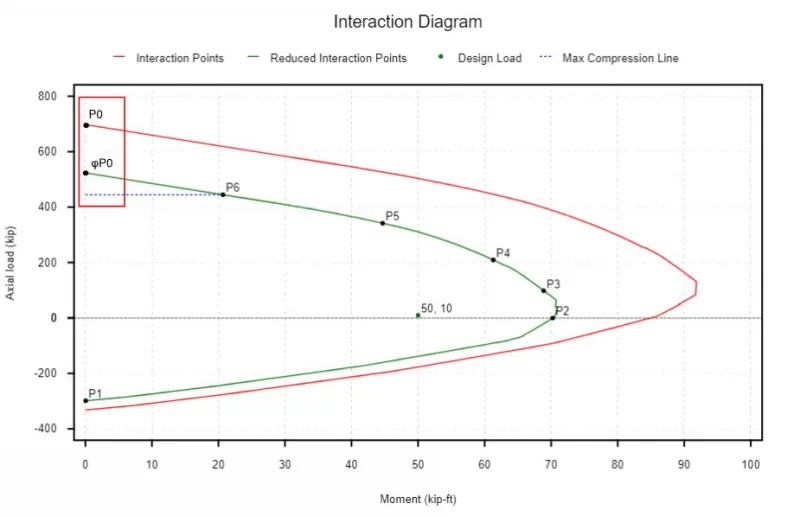
Un diagramme d'interaction est une représentation graphique de la capacité de résistance d'une colonne sous la flexion combinée et les charges axiales.
Les sections suivantes de cet article décriront comment calculer le diagramme d'interaction pour une colonne renforcée à la main. En suivant les principes pour générer le diagramme d'interaction laissera le lecteur à une meilleure compréhension des points clés d'un diagramme d'interaction et comment interpréter les résultats du diagramme d'interaction pour un concept de colonne de béton.
La génération d'un diagramme d'interaction à la main pour chaque section de colonne peut prendre du temps, de sorte que des logiciels comme la calculatrice de colonne de béton skyciv existent automatiquement pour générer automatiquement des diagrammes d'interaction pour les colonnes concrètes et évaluer également l'utilisation en fonction des charges de conception sans nécessiter un utilisateur pour vérifier manuellement l'interaction diagramme.
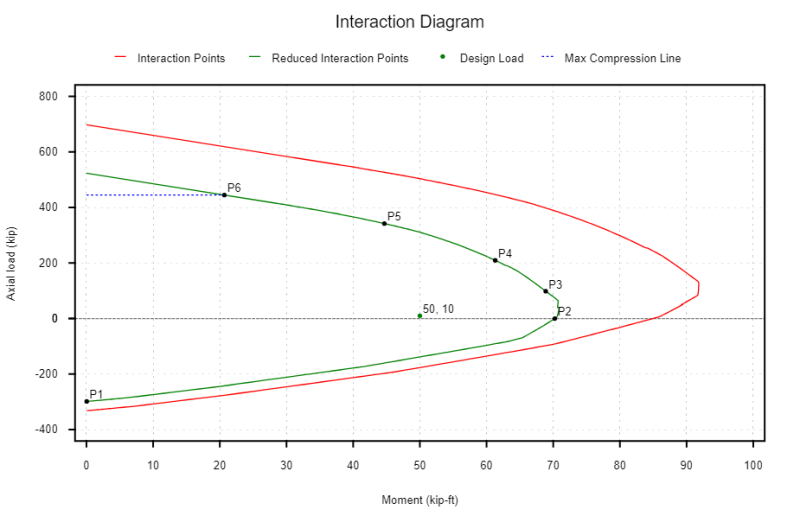
Comment créer un diagramme d'interaction
La création d'un diagramme d'interaction consiste à évaluer la colonne de béton armé pour les cas suivants:
- (P1) Tension pure - Il s'agit de la plus grande charge de tension axiale que la colonne peut supporter.
- (P2) Pur pur - La section est soumise à un moment de flexion m et à la force axiale de p = 0
- (P3) Point équilibré (et = ety) - Une condition équilibrée est atteinte lorsque la défaillance du béton se produit en même temps que l'acier à traction extrême donne.
- (P4) Point de demi-rendement (et = 0.5 ety) - Ceci est une position intermédiaire pour aider à tracer un diagramme d'interaction précis.
- (P5) Point de décompression (et = 0) - Ce cas marque la position lorsque les épisodes de tension remontent à des épisodes de compression (ACI). Les barres sont en transition entre la prise de certaines forces de tension pour ne prendre que des forces de compression.
- (P6) Compression pure - Il s'agit de la plus grande charge de compression axiale que la colonne peut supporter.
Notre diagramme d'interaction peut également prendre en considération le facteur de réduction de sécurité requis dans notre conception. Quelque chose que nous pouvons remarquer dans le diagramme d'interaction ci-dessus est que nous avons un facteur de sécurité plus important dans la région contrôlée par compression (0.65 ou 0.75) que nous le faisons dans la région contrôlée de tension (0.9).
Facteurs de réduction pour la conception de colonnes en béton selon ACI 318-19
Le facteur de réduction de la résistance (la spécification fournit un traitement intégré de la conception de la résistance admissible) Utilisé pour le moment, La force axiale ou le moment combiné et la force axiale dépendent de la façon dont la section est classée.
La section est classée par rapport à la souche de traction nette (et) qui est la tension dans le renforcement la plus proche de la face de tension:
- Tension contrôlée : et ≥ Ety + 0.003
- Transition : ety < et < ety + 0.003
- Compression contrôlée εt <= ety
En raison du changement du facteur de réduction de la résistance, il peut également être utile pour calculer le point de contrôle de la compression (P3 dans le diagramme précédent) et le point de contrôle de la tension (et ≥ Ety + 0.003) non étiqueté.
Il dépend également de notre renforcement transversal. Pour les spirales confirmant à 25.7.3 Nous pouvons obtenir Phi en fonction de notre εt comme:
- Tension contrôlée: φ = 0.9
- Contrôlé par compression: φ = 0.75
- Transition: φ = 0.75 + 0.15 (et - ety ) / 0.003
Pour d'autres types de renforcement transversal:
- Tension contrôlée - φ = 0.9
- Contrôlé par compression - φ = 0.65
- Transition = φ = 0.65 + 0.25 (et - ety ) / 0.003
(En fait, la formule de transition est une fonction linéaire simple qui dépend de la proximité du point de compression ou de contrôle de la tension.)
Comment calculer la capacité de compression pure d'une colonne en béton
La capacité de compression pure ou la charge de courge est la résistance de la colonne sous charge axiale pure.
En utilisant l'ACI 318-19 section 22.4.2 Nous pouvons calculer la charge de compression pure pour une colonne de béton en utilisant la formule suivante:
P0 = 0.85 F'c * (Ag - Ast) + FY * Ast
où:
- F'c est la résistance à la compression en béton
- FY est la limite d'élasticité des barres d'armature
- Ag est la surface brute de la section
- Ast est la superficie totale de la barre d'armature en acier
- (Ag - Ast) est la zone transversale efficace du béton.
Ce point correspond à la partie supérieure à gauche du diagramme d'interaction sans facteur de réduction de résistance appliquée. Nous pouvons réduire cette valeur par notre facteur de réduction de résistance pour la région contrôlée par compression (Puisque nous sommes en pure compression, nous sommes certainement dans la région contrôlée par compression). L'ACI 318-19 Cependant, impose une limite maximale au-delà de cela qui est donnée par la ligne bleu en pointillés et est couverte dans la section suivante.
Comment calculer la capacité de compression maximale autorisée d'une colonne en béton (ACI)
Pour tenir compte de l'excentricité accidentelle, l'ACI 318-19 limite la compacité de compression maximale autorisée d'une colonne de béton armé pour 80 à 85 pour cent de la capacité de compression nominale pure calculée dans la section précédente.
La réduction dépend du type de membre et de l'armature transversale utilisée dans la colonne (voir table 22.4.2.1 de l'ACI 318-19).
Généralement, nous avons ce qui suit où les armatures transversales sont liées:
- Pn,max = 0.80 * P0
Ou si le renforcement transversal est des spirales:
- Pn,max = 0.85 * P0
Comment calculer la capacité de tension pure d'une colonne en béton (ACI)
La résistance à la tension de la colonne en béton armé provient entièrement de la résistance du renforcement et est proportionnelle à la zone de renforcement que nous avons.
La formule pour calculer la résistance à la tension axiale d'une colonne en béton armé est simplement:
PNT,max = fY * Ast
&
P1 = φ * PNT,max
Étant donné que la section est en tension pure et que toutes nos barres sont considérées comme donnant la section, la section est contrôlée par la tension et que le facteur de réduction de résistance φ est toujours 0.9.
Comment calculer la capacité du point d'équilibre d'une colonne en béton
Le point d'équilibre est défini comme la charge qui fait que l'élément de tension extrême donne d'abord εt = ety au même moment que le béton donne. La méthode utilisée pour calculer la résistance à la colonne (pour la flexion et la compression ou la tension axiale) À ce stade est la même que la méthode utilisée pour d'autres points avec un ε spécifiquet (e.g. εt = 0, et = 0.5 εty).
Nous pouvons d'abord calculer la contrainte de rendement du renforcement à l'aide de la loi de crochets:
εty = fY / E
Pour un 60 Bar ksi avec un module de jeunes de 29000 ksi nous avons une souche de rendement de
εty = 60/290000 = 0.00207
Nous prenons également toujours la contrainte de rendement pour le béton 0.003 (défini dans la section 22.2.2.1 de l'ACI 318-19).
En utilisant ces deux valeurs, nous pouvons tracer notre diagramme de déformation et en fonction du diagramme de déformation, nous pouvons déterminer les contraintes de notre section. Le calcul des contraintes est couvert dans les deux sections suivantes.
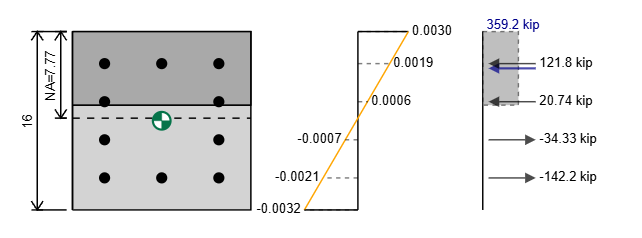
Comment calculer la force sur le renforcement dans la colonne de béton
Le calcul de la contrainte et de la force dans le renforcement est similaire à la façon dont nous avons calculé la résistance à la tension pure. Notre stress est égal à nos temps de déformation du module de notre jeune, mais est limité par notre limite d'élasticité.
σ = min( et * E , ety * E )
Nous pouvons alors déterminer la force sur nos barres en multipliant le stress par la zone des barres dans cette ligne. Pour simplifier les calculs où nous avons plusieurs barres avec la même contrainte que nous pouvons les regrouper toutes ensemble.
Ft = σ * A
Nous avons besoin d'un moyen de faire la distinction entre notre force en compression ou en tension. Nous pourrions utiliser FT et FC pour désigner les différentes forces, mais pour cet exemple et dans le calculatrice de SkyViv, nous utiliserons une notation de signe de négatif représentant la tension et la compression positive.
Comment calculer la force sur un bloc de contrainte en béton
Le calcul de la contrainte sur le composant en béton de notre colonne de béton armé est légèrement plus compliqué car la distribution de contrainte pour une section en béton n'est pas linéaire et est à la place approximativement parabolique. Heureusement, Il existe une simplification empirique pour le calcul des contraintes sur la section en béton connue sous le nom de méthode de blocs de contraintes de Whitney. Dans cette méthode, nous approximations de la distribution de stress parabolique en tant que bloc de contrainte rectangulaire.
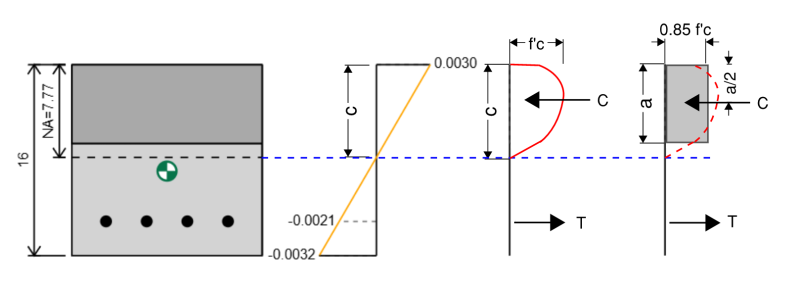
L'ACI décrit cette méthode dans la section 22.2.2.4.1. Nous calculons A comme:
A = b1 * c
où β1 va de 0.65 à 0.85 en fonction de la résistance à la compression (f'c) de béton (voir table 22.2.2.4.3).
Lorsque nous calculons la force sur le bloc de contraintes, nous utilisons toujours une contrainte efficace de 0.85 * f'c.
Afin que nous puissions calculer la force de compression comme:
Fc = 0.85 * f'c * B1 * c
et la force agit à une position A / 2 à partir du bord de compression extrême.
Comment calculer la capacité axiale d'une colonne de béton à partir d'un diagramme de contrainte-déformation
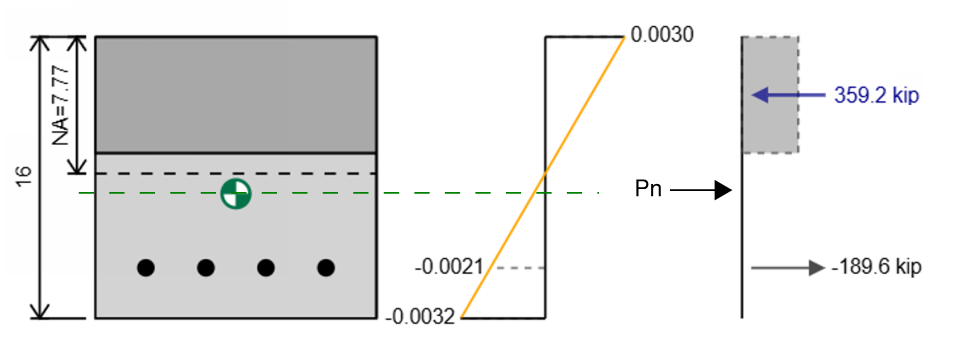
Nous avons maintenant toutes les souches, Stress et forces sur le renforcement et le béton dans notre section, mais nous n'avons toujours pas précisé la capacité axiale ou la capacité de flexion pour cette section.
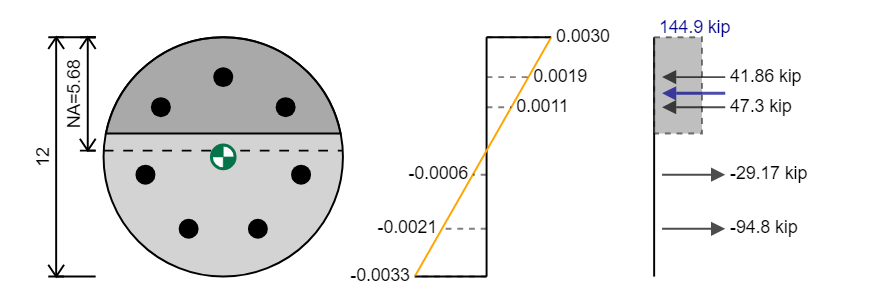
La capacité axiale est la force résultante et la position dans laquelle elle agit est le centroïde en plastique (Marqueur de centroïde vert en diagramme). Dans l'exemple ci-dessus, la capacité axiale est
Utiliser le principePles de statistiques, nous pouvons utiliser notre diagramme de force pour déterminer la capacité de notre section. Nous pouvons d'abord utiliser la somme des forces pour déterminer la capacité axiale, sachant que nos forces de compression totales doivent être égales à notre tension totale pourcés.
Σfx = 0 → σc = σt
Nous pouvons ensuite résumer les forces de compression en acier et la force de compression en béton et les forces de tension en acier pour découvrir la force résultante qui est la capacité axiale de notre section.
Pn = σc - Σt
Par exemple, si nous avons 359.2 kip de compression et 189.6 kip de tension Pour la section, la force résultante est 359.2 - 189.6 = 169.6 kip. Notez que la force dessinée qui équilibre complètement la section (c'est-à-dire une force de tension de 169.6) est l'opposé de la capacité qui est 169.6 Kip en compression puisque nous pouvons
Comment calculer la capacité de flexion d'une colonne en béton à partir d'un diagramme de contrainte-détresse
Nous savons maintenant que nous avons besoin d'une force agissant sur notre section pour l'équilibrer. Cette force agit au centre de centroïde en plastique de la section qui est marquée par le marqueur de centroïde vert dans le dessin ci-dessus.
Pour trouver le centroïde en plastique, les calculs sont les mêmes que pour un calcul de centroïde normal sauf au lieu de multiplier A par une distance, nous avons plusieurs f par une distance.
Pour calculer la capacité de flexion, nous pouvons prendre des instants sur n'importe quelle position et nous aurons un moment net. Nous pouvons prendre les moments de la position du centroïde en plastique afin que nous n'ayons pas à nous soucier de la force PN dans nos calculs, car son levier serait 0. Un tableau peut être utile pour ces calculs, en particulier lorsque nous avons de nombreuses couches de renforcement.

Nous pouvons voir que les calculs de notre capacité de moment sont
Mn = Σf x levier = 359.2 X 5.615/12 + -189.6 X -4.206/12 = 168.1 + 66.5 = 234.6 kip-ft
Un moment positif signifie que le haut de la section est en compression et que le bas de la section est en tension.
Comment calculer la capacité de flexion et axiale réduite de la colonne de béton
Nous avons calculé une capacité de moment de 234.6 kip-ft et une capacité de compression de 169.6 kip cependant, ce sont nos capacités ultimes et doivent être réduites par un facteur de réduction de la force Phi.
Puisque nous envisageons actuellement le point d'équilibre et que nous avons εt = εty, nous sommes dans la région contrôlée par compression et devons utiliser un facteur de sécurité de 0.65 ou 0.75 en fonction de l'armature transversale dans la colonne de béton armé.
Tracer un diagramme d'interaction
Jusqu'à présent, nous avons vu comment calculer
- (P1) Point de tension pure
- (P6) Point de compression pure
- (P3) Point équilibré
En utilisant la même procédure que le calcul du point équilibré, nous pouvons également calculer la capacité axiale et de flexion pour:
- (P4) Point de demi-rendement
- (P5) Point de décompression
La différence entre ces trois points (P3, P4, P5) est simplement l'hypothèse initiale que nous faisons en générant le diagramme de déformation à chaque étape qui suit d'être la même.
Avec ces cinq points déterminés, le seul point pour lequel nous n'avons pas calculé est le point de flexion pur. Ce point correspond au point où nous avons pn = 0 Dans notre section. Pour déterminer ce point, nous avons besoin d'une solution itérative où nous devinons une position de l'axe neutre (Valeur de C dans ACI) et déterminer si pn = 0. Une fois que nous avons trouvé cette position de l'axe neutre, nous pouvons ensuite continuer nos étapes comme nous l'avons fait pour le point d'équilibre.
Avec chaque valeur déterminée, nous pouvons ensuite générer un diagramme d'interaction pour notre colonne de béton armé. Nous pouvons simplement dessiner nos points clés et tracer une ligne droite entre eux pour créer un schéma d'interaction simple. Avec des logiciels comme la calculatrice de colonne de béton de conception rapide de Skyciv, nous pouvons générer beaucoup plus de points dans le diagramme d'interaction plutôt que les points clés qui peuvent donner comme un tracé plus lisse et plus précis.
Un autre point qui peut être utile pour tracer lors de la conception de l'ACI 318-19 est le point de transition du contrôle de la tension car c'est là que le facteur PHI commence à changer comme il le fait en position P3 qui est le point de transition du contrôle de compression. Notez également que parce qu'il y a une réduction de la force de compression pure maximale autorisée (indiqué par la ligne bleue) La force de compression maximale peut également résister à une capacité de moment indiquée par le point P6 dans le graphique ci-dessous.
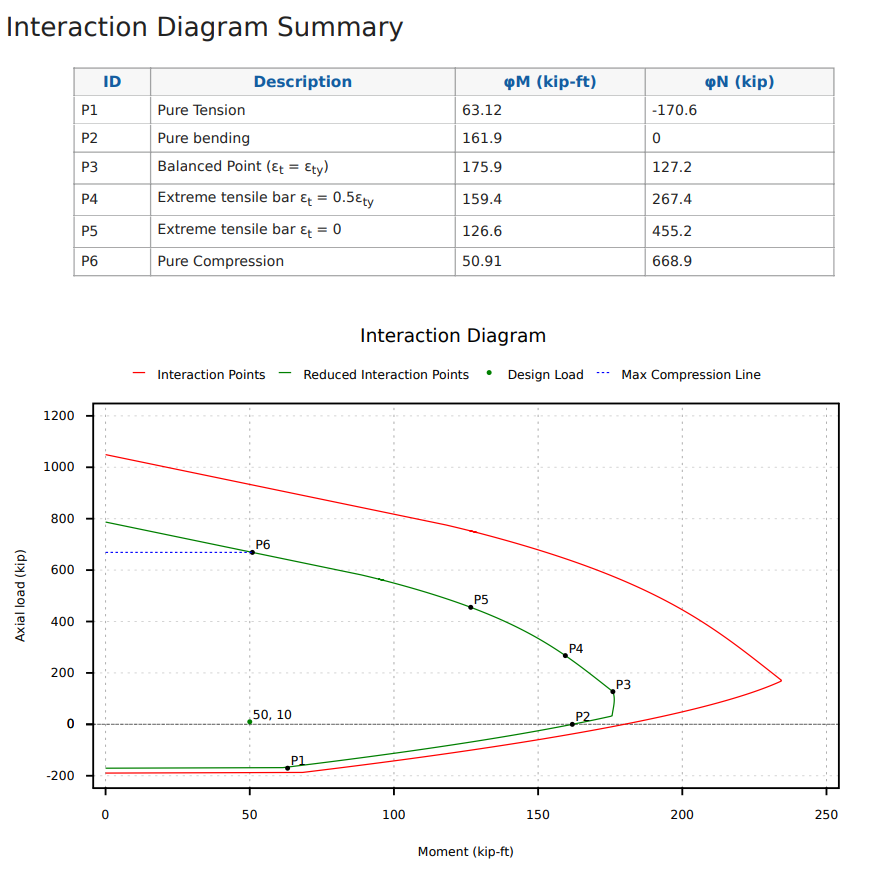
Comment lire un diagramme d'interaction?
Jusqu'à présent, nous avons beaucoup appris sur la façon de créer un diagramme d'interaction, mais comment pouvons-nous l'utiliser dans notre conception et pourquoi est-ce nécessaire.
En fin de compte, Le diagramme d'interaction est utile car il est toujours le même pour notre section (Lorsque vous se penchez dans une certaine direction) et ne dépend pas des variations de notre force axiale et de notre moment.
Si nous devions calculer que si notre section avait une capacité pour une seule combinaison de force axiale et de moment, nous pourrions ne pas avoir besoin du diagramme, mais cela fera des calculs très répétitifs si nous avons plusieurs combinaisons et forces de charges différentes que nous voulons envisager.
Le diagramme d'interaction fournit une utilisation avec un outil visuel qui nous permet de déterminer rapidement si une certaine combinaison de chargement répond aux exigences de la norme de conception que nous utilisons comme l'ACI 318-19. Tout ce que nous devons faire est de tracer notre point et de nous assurer qu'il se trouve à l'intérieur de la zone de notre diagramme d'interaction, Et nous pourrions tracer de nombreuses combinaisons de charges différentes en même temps.
Les ratios d'utilisation sont légèrement arbitraires car nous sommes principalement préoccupés par si nous sommes à l'intérieur de la zone ou non, Cependant, nous pouvons définir des ratios d'utilisation par jusqu'où nous sommes d'une frontière particulière. Notre distance dans l'axe x est notre utilisation du moment pour le diagramme d'interaction et notre distance dans l'axe Y est notre utilisation axiale pour le diagramme d'interaction.
Comment créer un diagramme d'interaction pour la flexion biaxiale sur une colonne en béton
Le diagramme d'interaction que nous avons examiné auparavant était pour la flexion uniaxiale d'une section en béton armé rectangulaire. Nous avons seulement considéré que la flexion se déroule sur un seul axe, mais nous pourrions également avoir une flexion de l'axe mineur. Pour la flexion des axes mineurs, nous ferions tout de même, sauf que nous tournions la section 90 Degrés donc à la place, nous aurions quelque chose comme ça.
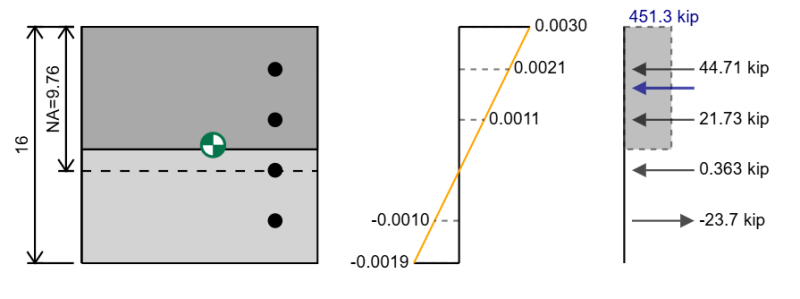
Pour la flexion biaxiale, nous devons faire pivoter notre section afin qu'il se plie autour du plan de son moment résultant. Le diagramme d'interaction que nous obtiendrions pour ce diagramme biaxial n'est pertinent que pour cette direction particulière du moment résultant.
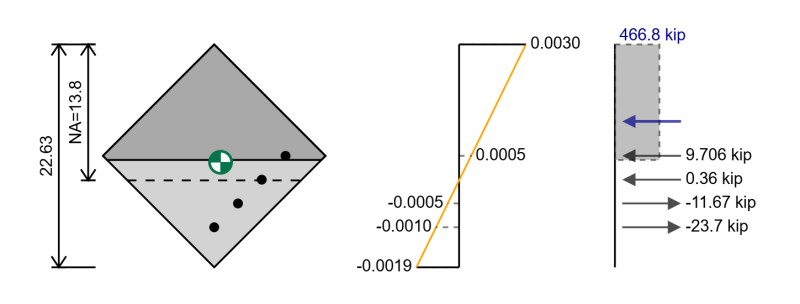
Nous pouvons suivre les mêmes étapes que nous l'avons fait pour le diagramme d'interaction auparavant, sauf que maintenant nous aurons différentes positions pour notre renforcement et dans le cas d'une section rectangulaire dans la flexion biaxiale, nous avons une zone triangulaire qui est en compression.
Au lieu de calculer la force de compression en béton comme:
Fc = 0.85 * f'c * B1 * c
Nous pouvons plutôt calculer la force de compression du béton comme:
Fc = 0.85 * f'c * A
où a est la zone en compression au-dessus de la position a = β1 * c
Qu'est-ce qu'un diagramme d'interaction 3D?
L'une des limites de la création d'un diagramme d'interaction 2D pour la flexion biaxiale est qu'il n'est pertinent que pour une direction du moment qui résulte particulier. Nous avons maintenant trois variables dans la considération de notre capacité, pourquoi sont MZ, Mon et n. Naturellement au lieu d'utiliser un graphique 2D qui ne peut gérer que deux axes et donc deux variables, nous pouvons plutôt créer un diagramme d'interaction tridimensionnel qui peut gérer trois variables.
Comme le diagramme d'interaction 2D, notre objectif est d'avoir nos combinaisons de chargement à l'intérieur de la zone du graphique, la différence étant maintenant que nous avons trois points à considérer (Mz, ma,N) Et notre point doit être contenu dans notre volume de diagramme d'interaction (plutôt que la zone). Il s'agit d'un outil visuel utile pour évaluer plusieurs points en même temps, mais sa limitation est qu'il est difficile à utiliser dans des supports 2D tels que des graphiques ou des images statiques et un logiciel interactif est nécessaire pour utiliser pleinement un tel graphique. Skyciv Section Builder peut aider à générer des diagrammes d'interaction 3D qui sont faciles à travailler avec.
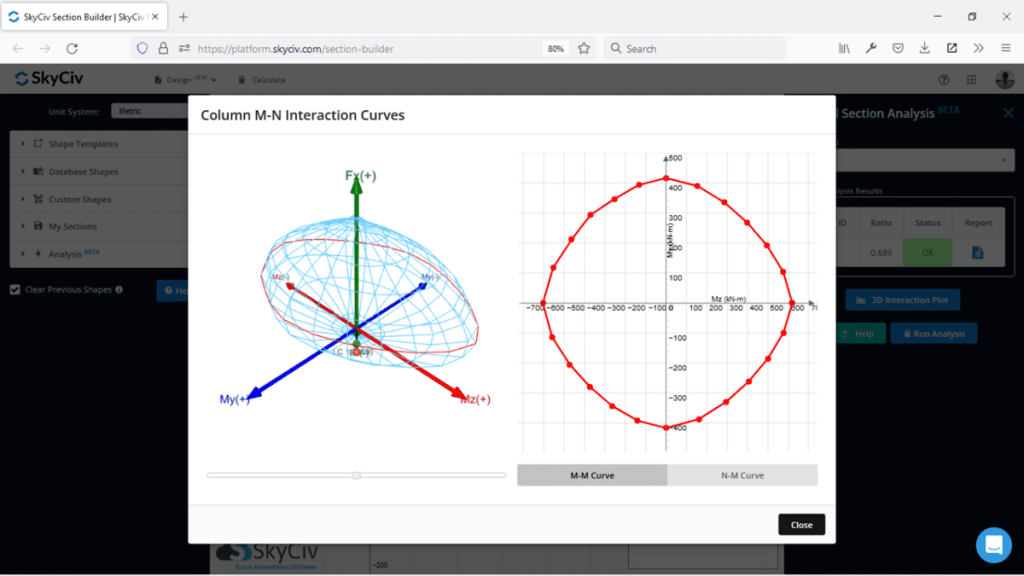
Comment créer un diagramme d'interaction 3D
Pour obtenir tous les points de données dont nous avons besoin pour créer un diagramme d'interaction 3D, nous faisons la même évaluation 2D que nous avons fait auparavant, sauf que maintenant nous le faisons plusieurs fois alors que nous tournons progressivement la section autour. Nous pouvons utiliser la rotation que nous aimons, Un angle raisonnable pourrait être 15 diplômes qui nous donneraient 24 différents angles.
Obtenir les données à la main est fastidieux mais possible, mais utiliser ces données pour créer un diagramme d'interaction interactif 3D est extrêmement difficile. 3Les diagrammes d'interaction D sont mieux utilisés avec des logiciels comme Skyviv Section Builder.
Outils Similaires
- Calculateur de faisceau en béton
- Calculateur de Longueur de d'épissure des Armatures
- Calculateur de longueur de développement des barres d'armature
- Calculateur de Corbeau en Béton
- AS 2870 Logiciel de Conception de Dalle Résidentielle
- Calculateur de Cisaillement Poinçonnant
- Calculateur de Conception de Semelle
- ACI 360 Logiciel de Conception de Dalle sur Sol
À propos de SkyCiv
SkyCiv propose une large gamme de logiciels de conception et d'analyse structurelle en cloud pour les ingénieurs. En tant qu'entreprise technologique en constante évolution, nous nous engageons à innover et à remettre en question les méthodes de travail existantes pour faire gagner du temps aux ingénieurs dans leurs processus de travail et leurs conceptions.