Τι είναι η ανάλυση P-Delta?

  Η ανάλυση P-Delta είναι ένας τύπος ανάλυσης που είναι ιδιαίτερα σημαντικός για την πλευρική μετατόπιση πολυόροφων κτιριακών κατασκευών που αντιμετωπίζουν βαρύτητα. Σε αυτό το άρθρο, Λογισμικό SkyCiv Online Engineering θα συζητήσει την απλή θεωρία πίσω από τα αποτελέσματα P-Delta και θα σας βοηθήσει να κατανοήσετε τη σημασία μιας τέτοιας ανάλυσης κατά τη μοντελοποίηση των δομών σας.  

Τι είναι τα εφέ P-Delta?

Φυσικά, οποιοδήποτε δομικό μοντέλο θα παραμορφωθεί όταν φορτωθεί. Μια παραμορφωμένη δομή μπορεί να συναντήσει σημαντικές δευτερεύουσες ροπές επειδή τα άκρα των μελών έχουν αλλάξει θέση. Για παράδειγμα, εξετάστε το απλό παράδειγμα στήλης με πρόβολο που φαίνεται παρακάτω: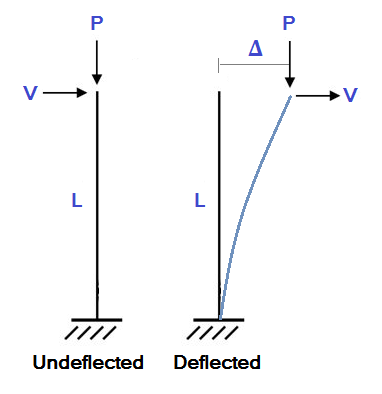 Σε αυτό το παράδειγμα, μια στήλη μήκους L αντιμετωπίζει αξονικό φορτίο (Π) και ένα πλευρικό φορτίο (Β). Σε μια τυπική γραμμική στατική ανάλυση θα υπολογίζαμε την πλευρική παραμόρφωση (Δ) όπως και: [μαθηματικά] \Δέλτα = dfrac{ML ^ 2}{3ΟΧΙ} = dfrac{VL ^ 3}{3ΟΧΙ} \κείμενο{ από το M = VL} [μαθηματικά] Παρατηρήστε ότι στην περίπτωση γραμμικής στατικής ανάλυσης η πλευρική παραμόρφωση, Δ, εξαρτάται από το πλευρικό φορτίο (Β). Ωστόσο, εάν η στήλη αντιμετωπίζει αξονικό φορτίο (Π), τότε η στήλη δεν εκτρέπεται ακόμη περισσότερο? Αυτό είναι προφανές επειδή το αξονικό φορτίο θα προκαλούσε μια δευτερεύουσα ροπή με τιμή P × Δ. Για παράδειγμα, ας συνοψίσουμε τις στιγμές για τη βάση της στήλης: [μαθηματικά] \άθροισμα{Μ}=(V φορές L) + (P φορές Δέλτα)= VL + P Δέλτα \\\\ Μ_{1} = VL \\\\ Μ_{2} = P Δέλτα [μαθηματικά] Εδώ Μ₁ οφείλεται στο πλευρικό φορτίο σημείου ενώ, Μ₂ οφείλεται στο αξονικό φορτίο. Κάθε μία από αυτές τις στιγμές συμβάλλει στην πλευρική παραμόρφωση με διαφορετικό τρόπο (μπορείτε να αναζητήσετε τους τύπους προβόλου για την απόκλιση στο τέλος λόγω φορτίου σημείου και στιγμής, αντίστοιχα για αυτούς τους τύπους): [μαθηματικά] \Δέλτα_{1} = dfrac{Μ_{1}Λ ^ 2}{3ΟΧΙ} = dfrac{VL ^ 3}{3ΟΧΙ} \\\\ \Δέλτα_{2} = dfrac{Μ_{2}Λ ^ 2}{2ΟΧΙ} = dfrac{P Delta L ^ 2}{2ΟΧΙ} [μαθηματικά] Αλήθεια, η συνολική πλευρική παραμόρφωση θα ήταν πιο κοντά: [μαθηματικά] \Δέλτα_{νέος} = Δέλτα_{1} + \Δέλτα_{2} = dfrac{VL ^ 3}{3ΟΧΙ} + \dfrac{P Delta L ^ 2}{2ΟΧΙ} [μαθηματικά] Μπορούμε να το δούμε σε σύγκριση με την αρχική τιμή εκτροπής, υπάρχει ένας επιπλέον όρος στα δεξιά με όρους P και Δ. Εάν το P ή το Δ είναι σημαντικές τιμές, η τυπική γραμμική στατική ανάλυση θα υποτιμούσε την παραμόρφωση της στήλης. Θα πρέπει να είναι προφανές τώρα ότι η ανάλυση P-Delta πήρε το όνομά της από τη δευτερεύουσα στιγμή PΔ. Επομένως, Τα εφέ P-Delta προκαλούνται από γεωμετρική μη γραμμικότητα. Γι 'αυτό το λόγο, Η ανάλυση P-Delta ονομάζεται συχνά α Μη γραμμική ανάλυση. Μια σωστή ανάλυση P-Delta θα συνέχιζε να επαναλαμβάνει την παραπάνω διαδικασία για να ενημερώσει την τιμή του Δ_νέος.

Πότε πρέπει να ανησυχώ για τη διεξαγωγή ανάλυσης P-Delta?

Τα καλά νέα είναι ότι SkyCiv Structural 3D μπορεί τώρα να πραγματοποιήσει μια ανάλυση P-Delta για εσάς. Τα φαινόμενα P-Delta συνήθως επικρατούν σε ψηλές κατασκευές που αντιμετωπίζουν φορτία βαρύτητας και πλευρική μετατόπιση λόγω ανέμου ή άλλων δυνάμεων. Εάν η πλευρική μετατόπιση και / ή τα κατακόρυφα αξονικά φορτία μέσω της κατασκευής είναι σημαντικά, Πρέπει να πραγματοποιηθεί ανάλυση P-Delta για να ληφθούν υπόψη οι μη γραμμικότητες. Σε πολλές περιπτώσεις, μια γραμμική στατική ανάλυση μπορεί υποτιμά σοβαρά μετατόπιση (μεταξύ άλλων αποτελεσμάτων) σε σύγκριση με ένα P-Delta (Μη γραμμικό) Ανάλυση. Η σημασία μιας μη γραμμικής ανάλυσης P-Delta θα παρουσιαστεί στο παρακάτω παράδειγμα. Το πολυώροφο πλαίσιο του κτηρίου έχει ύψος 20μ, με κάθε όροφο ύψους 5 μέτρων. Οι στήλες είναι πλήρως στερεωμένες στη βάση με κατανεμημένα φορτία σε κάθε επίπεδο. Επιπροσθέτως, Υπάρχουν κατακόρυφα φορτία στον τελευταίο όροφο και το ίδιο βάρος θεωρείται ότι μπορούν να προσομοιωθούν φορτία βαρύτητας. Υπάρχει επίσης ένα σχετικά μικρό πλευρικό φορτίο που εφαρμόζεται στην πλευρά της κατασκευής.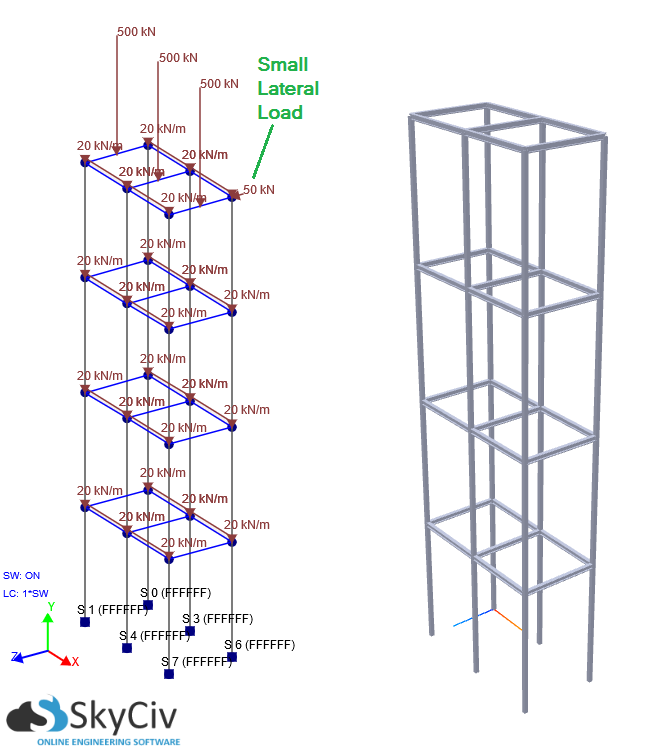   Υπό αυτές τις συνθήκες, ας συγκρίνουμε τα αποτελέσματα μεταξύ γραμμικού και P-Delta (Μη γραμμικό) Ανάλυση:

	Γραμμικός	Π-Δέλτα (Μη γραμμικό)	% Διαφορά
Μέγιστη συνολική μετατόπιση	254 χιλ	353 χιλ	+ 39%
Μέγιστη κάθετη αντίδραση	629 ΚΝ	668 ΚΝ	+ 6%
Μέγιστη Αντίδραση Στιγμής	42 kN-m	60 kN-m	+ 43%

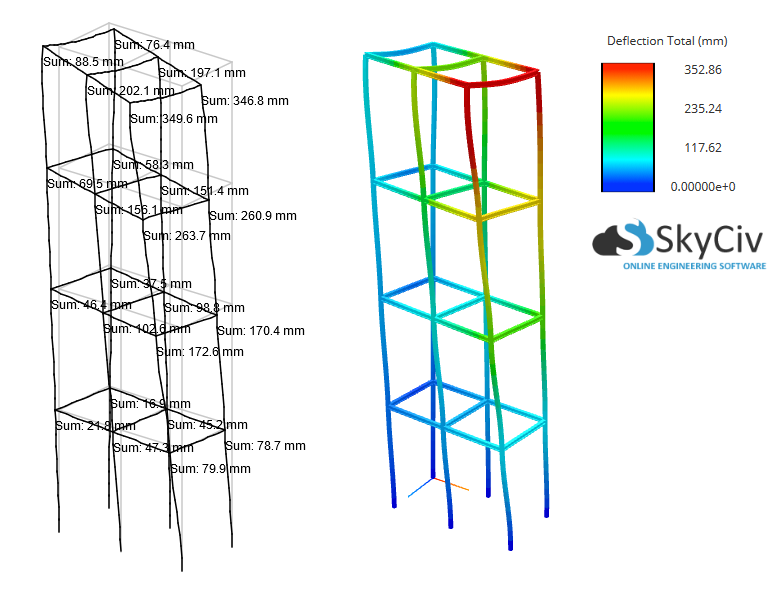Είναι σαφές ότι τα εφέ P-Delta παίζουν εξαιρετικά σημαντικό ρόλο με αυτήν τη δομή, αυξάνοντας τα αποτελέσματα μέγιστης απόκλισης και μέγιστης ροπής κατά περίπου 40%! Ετσι, μια γραμμική στατική ανάλυση είναι ανεπαρκής σε μια τέτοια περίπτωση. Συνοψίζοντας, Η ανάλυση P-Delta είναι προτιμότερη από τη Γραμμική Στατική Ανάλυση καθώς αντιπροσωπεύει απρόβλεπτες μη γραμμικότητες στο μοντέλο σας. Μπορείς να χρησιμοποιήσεις SkyCiv Structural 3D για γρήγορη και αποτελεσματική ανάλυση P-Delta στα μοντέλα σας; απλά επιλέξτε "Ανάλυση P-Delta" όταν κάνετε κλικ "Λύσει." Αφήστε το λογισμικό να κάνει τη δουλειά για εσάς, οπότε το μόνο που έχετε να ανησυχείτε είναι ο σχεδιασμός!  

ΕΓΓΡΑΦΕΙΤΕ ΔΩΡΕΑΝ