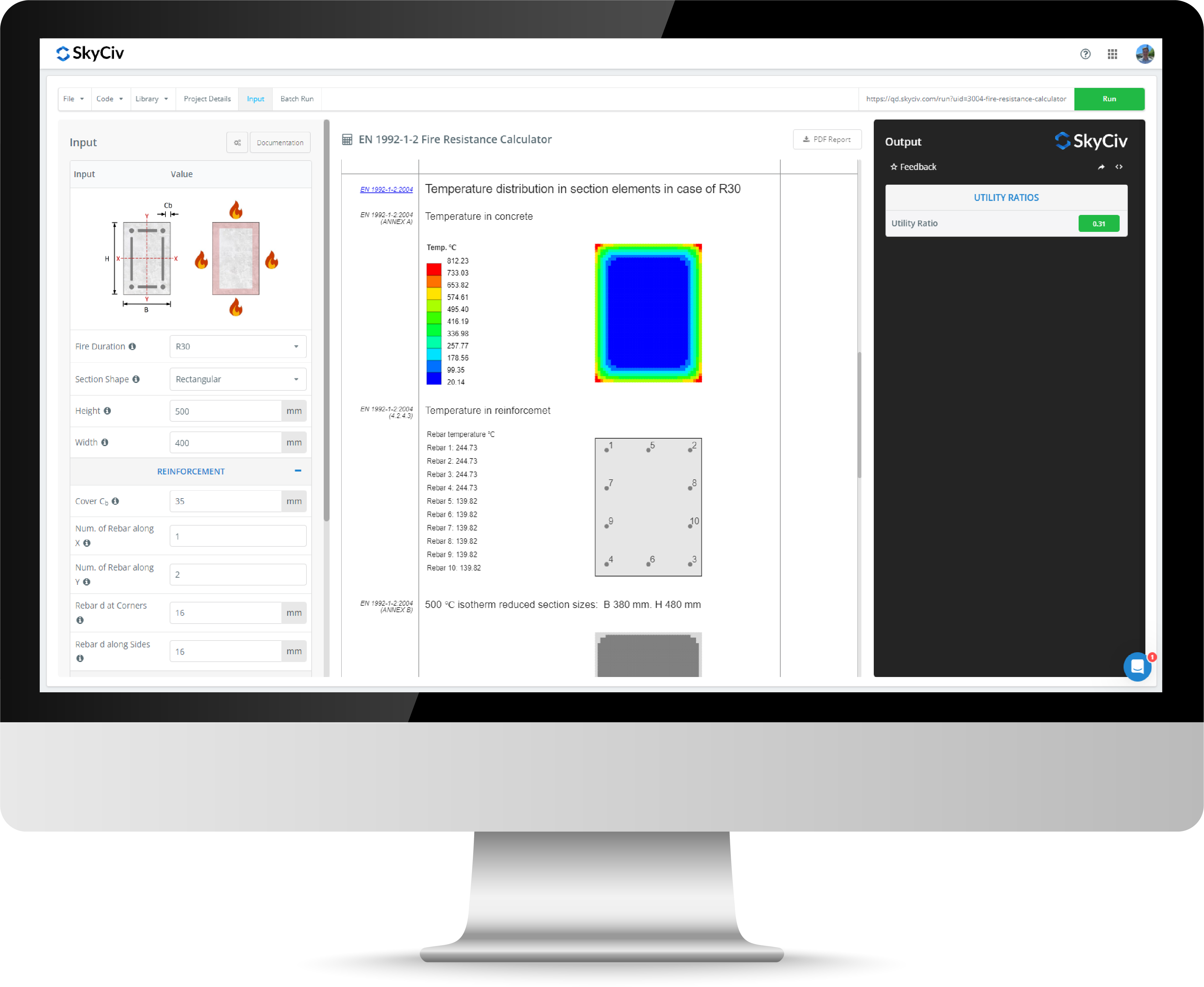
Abschnittseigenschaftenrechner
Mit dem SkyCiv-Schnitteigenschaftenrechner können Sie schnell und genau die Schnitteigenschaften für die folgenden Querschnitte ermitteln:
- Ich strahle (I-Abschnitte, W-Formen, Ich-Form)
- T-Formen
- Kanäle (Baustahlelemente werden durch Füllelemente oder Verbinder, die Winkelprofile sein können, miteinander verbunden)
- Winkel
- Rechteckige Hohlprofile (RHS)
- Kreisförmige Hohlprofile (CHS)
- Feste Rechtecke und Kreise
Dieser Rechner wurde anhand einer Reihe von Produkten validiert und getestet, Handberechnungen und bekannte Werte, um die Genauigkeit der Berechnung der folgenden Werte sicherzustellen:
- Trägheitsmoment
- Bereich
- Schwerpunkt
- Abschnittsmodul
Schwerpunktrechner
Der oben genannte Schwerpunktrechnungsrechner verwendet die relevanten Schwerpunkte, um den Schwerpunkt eines Kreises zu ermitteln, Rechteck, hohl rechteckig, Ich strahle, Kanäle und Winkelabschnitte. Der Taschenrechner gibt vereinfachte Ergebnisse einschließlich des Zentroids zurück (in sowohl in x als auch in y Richtungen) Aus einigen einfachen Abschnittsdimensionseingängen. Der Abschnitt Zentroid ist das geometrische Zentrum einer Form, Darstellung des Punktes darstellen, an dem sein Gebiet gleichmäßig ausgeglichen werden kann. Angenommen ein konsistentes Material innerhalb des Abschnitts, Es wird der Schwerpunkt für diesen Abschnitt sein. Der Schwerpunkt wird normalerweise als CX und Cy definiert, den Abstand vom Boden des Abschnitts in x bzw. y darstellen. Der Schwerpunkt der Schwerpunkt kann also als Punkt bezeichnet werden [CX, Cy].
Für einige Formen, Dies ist eine ziemlich einfache Berechnung. Zum Beispiel, Das Finden des Schwerpunkts eines Rechtecks ist so einfach wie die Höhe und Breite zu halben:
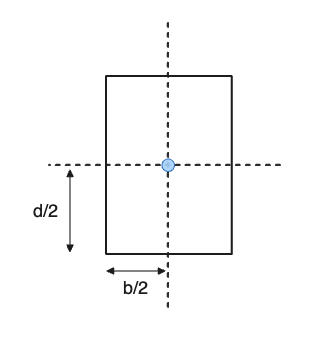
Jedoch, Für komplexere Abschnitte, in denen sie in beiden Achse nicht symmetrisch sind, Die Schwerpunktberechnungen sind etwas komplexer. Zum Beispiel, Ein Winkelabschnitt kann sich irgendwo im tatsächlichen Abschnitt befinden:
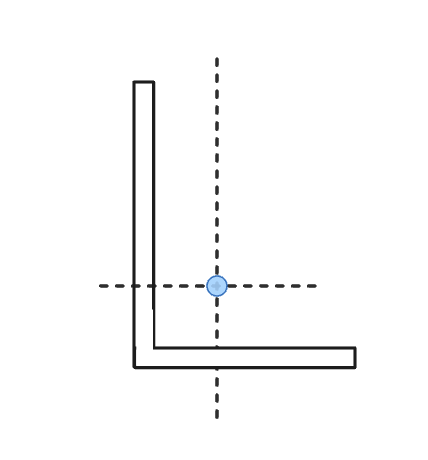
Abschnittsmodulrechner
Der Abschnittsmodul ist eine wichtige geometrische Eigenschaft, was letztendlich darstellt, wie gut ein Abschnitt Biegung widerstehen kann. Es wird durch die folgende einfache elastische Abschnittsmodulgleichung berechnet:
S.xb = Ixx / C.j
- S.xb: Abschnittsmodul zur x-Achse am Ende des Abschnitts
- S.XT: Abschnittsmodul über die X-Achse an der Spitze des Abschnitts
- S.yt: Abschnittsmodul zur y-Achse an der Spitze des Abschnitts (oder der rechtste Teil des Abschnitts)
- S.yb: Abschnittsmodul zur y-Achse am Ende des Abschnitts (oder der links am besten des Abschnitts)
Es ist auch wichtig zu beachten, Die x/z -Achse kann austauschbar verwendet werden. So zum Beispiel, In unserem Abschnitt Modulberechnungen, Wir verwenden mit anstatt x als unsere horizontale Achse.
Elastischer Querschnittsmodul (S.) Gegen Kunststoffabschnitt Modul (MIT)
Der elastische Abschnittsmodul (S.) repräsentiert das Biegeverhalten eines Abschnitts innerhalb seiner elastischen Grenze - wo es unter Last verformt, aber nach Entfernung der Last in seine ursprüngliche Form zurückkehrt. Dieser Modul ist entscheidend für die Berechnung der maximalen Biegespannung, bevor er nachgibt.
Andererseits, der Kunststoffabschnittsmodul (MIT) erfasst das Biegeverhalten eines Abschnitts darüber hinaus seine elastische Grenze, wo es plastische Verformungen unterzogen wird. Z stellt die Fähigkeit des Mitglieds dar, Stress nach der Erzielung von Stress umzuverteilen, Verbesserung des Biegenwiderstands.
Während s (elastisch) ist grundlegend für die Gestaltung von Strukturen, die in ihrem elastischen Bereich arbeiten, MIT (Plastik) Findet Anwendung in Szenarien, in denen plastisches Verhalten erwartet oder gewünscht wird, wie in Stahldesign im Umgang mit kompakten Abschnitten, Der Kunststoffabschnittsmodul kann verwendet werden, um das Design weiter voranzutreiben. Im Falle eines nicht kompakten Abschnitts, Der Abschnitt wird lokal anschnallen, bevor seine Kunststoffmomentkapazität erreicht ist - daher die Elastizitätsabschnittsmodul wird in diesem Fall verwendet. Sie können mehr darüber in Skycivs Leitfaden zu lesen AS4100 Stahldesign, Dies gibt zwar spezifische Hinweise auf die australischen Standards, Es hat nützliche allgemeine Kommentare zu Abschnittsklassifizierungen im Stahldesign.
Es ist auch wichtig zu beachten:
Australien
Z = elastisch, S = Plastik
Amerika + Rest der Welt
S = elastisch, Z = Kunststoff