在SkyCiv,我们认为教育很重要,因此我们致力于帮助下一代工程师学习结构工程. 作为这项使命的一部分, 作为这项使命的一部分, 将其暴露给我们用户的好奇心. 工程师喜欢知道事物的方式和原因, 和 通常最好的学习方法是尝试自己解决问题,并将解决方案与完整,正确的解决方案进行比较. 我们在报告的可读性和回溯计算所需的详细程度之间取得平衡, 一步步. 这是工程实践的基础,我们将继续为用户提供可增加其教育价值的工具, 作为这项使命的一部分, 作为这项使命的一部分.
我们由您想要的驱动: 用户最需要的功能之一是不确定梁的手动计算. 我们很自豪地宣布此功能现已启用: 现在的学生, 基本和专业用户可以 现在就试试. 用于不带铰链的不确定梁, 使用矩量分布法求解竖向和弯矩反应.
作为这项使命的一部分, 将轻松显示光束的手计算,如下所示:
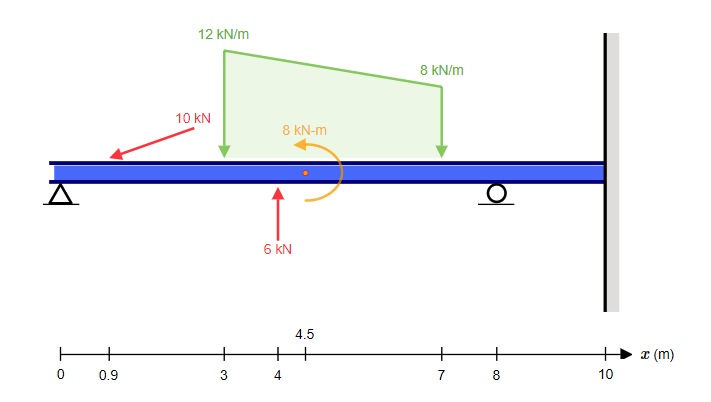
现有用户将熟悉在Beam中获取用于静态确定结构的手计算,但是, 如果您是SkyCiv的新手或尚未尝试过手动计算, 我们的 文件资料 可以指导您完成整个过程.
矩分配法
矩分配法 (MDM), 由Hardy Cross发明, 自从它由ASCE期刊于 1930. 其简单性的部分原因在于可以通过叠加方式以图形方式绘制弯矩图,而无需计算每个线段的不连续性方程式. 与其他方法(例如FEM)相比,可以轻松解决复杂的结构, 虚拟位移法, 或求解不连续性方程. MDM可用于各种2D结构,例如梁和框架.
哈迪克罗斯(Hardy Cross)是一段时间的结构工程师,当时手工计算对于任何结构工程师都是必不可少的练习. 在无数次重复计算结构的过程之后,他认识到他基本上是一次又一次地完成相同的计算. 这促使克罗斯探索了一个理论,即复杂结构实际上是简单结构的组合,并且, 这些简单的结构可以组装在一起,以相同的分析解决方案创建复杂的结构. 简单的结构很容易解决, 公式很容易推导,即使它们不确定, 得益于叠加和虚拟力法. 克罗斯创建了这些简单结构的表格,并以各种方式测试了他的理论.
固定端矩方程
矩分布法使用常见荷载工况表来查找各段末端的弯矩方程. 这些表可以在我们的文档中找到 计算弯矩图 不仅构成使用MDM的基础, 同时也为简单的弯矩计算提供了很好的参考. 一个简单的方法是, MDM将光束分成多个部分, 并使用这些简单方程式来计算BMD.
替代方法
计算弯矩图可以通过其他方式实现, 就像使用我们之前写的不连续方程 这里.
样品报告



