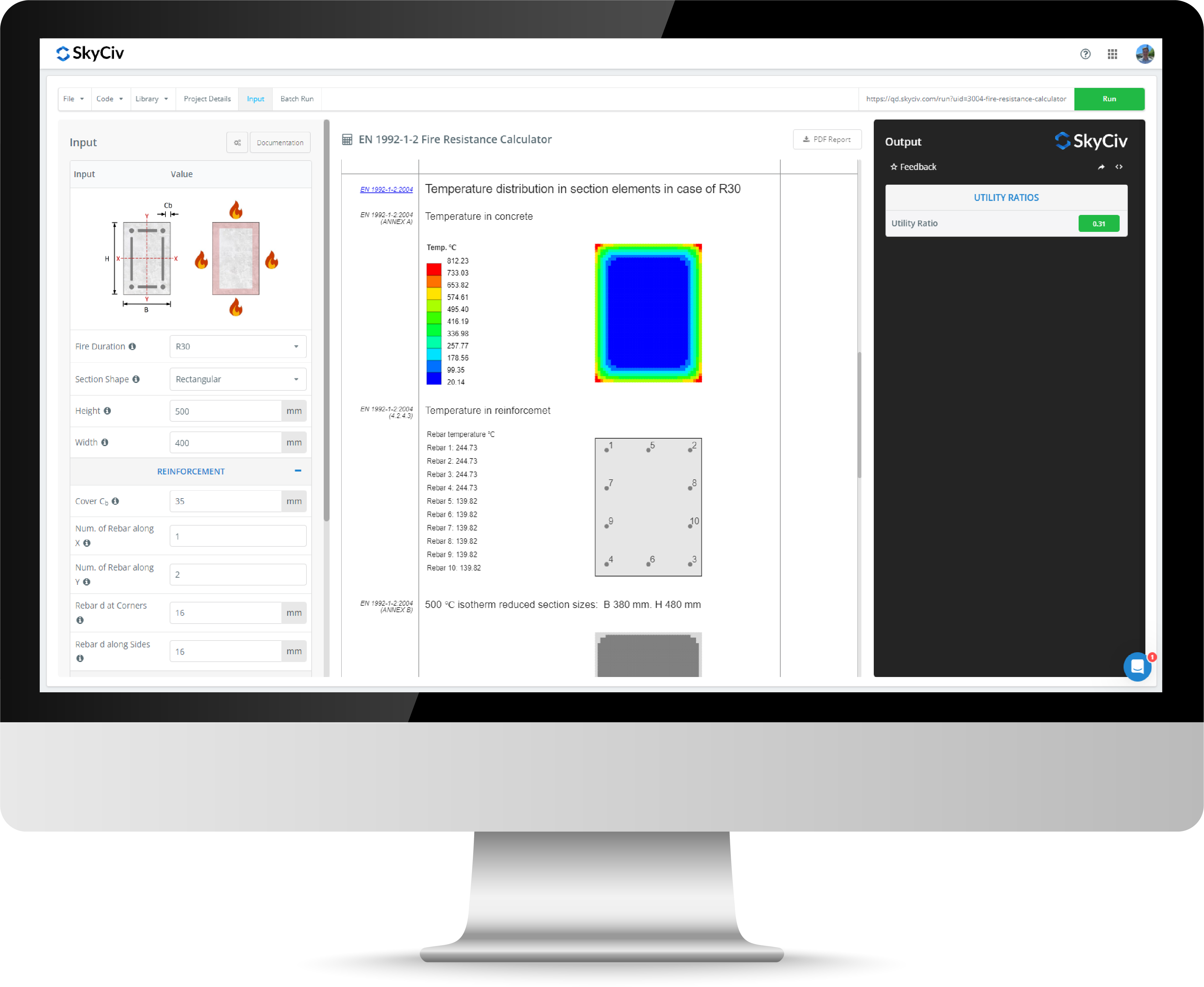
Betonarme Sütun Tasarım Hesap Makinesi
Skyciv takviyeli betonlu sütun hesap makinesi, Avrupalı, ve Avustralya Standartları. Betonarme sütunlar, beton ve çeliğin faydalarını ekonomik bir şekilde birleştiren kompozit bir bölümdür. Bir betonarme sütunun kompozit doğası, tasarım hesaplamalarını diğer bölümlerden daha titiz hale getirir ve hızlı tasarım beton sütun hesap makinesi, mühendislerin kapasiteleri değerlendirmeleri ve etkileşim diyagramları üretmeleri için kolay bir araç sağlar. aşağıdaki standartlar:
- Amerika Birleşik Devletleri - ACI-318-19: Yapısal Beton için Bina Kodu Gereklilikleri.
- Avustralya Standartları - GİBİ 3600-2018: Beton yapılar, Çelik & Tendonlar.
- Avrupa Standartları - Eurocode 2: temel olarak yayılmış temel boyutlarından etkilenir (İÇİNDE 1992-1-1:2004).
- Yeni Zelanda Standartları - NZS 3101:2006: Beton yapıların tasarımı
Bu standartlar arasında geçiş yapabilirsiniz. beton hesap makinesinin sağ üstü Sol taraf giriş panelinin üstünde bulunan bayrak simgesini kullanarak. Hesap makinesini çalıştırmak için, yazılımın sağ üst köşesindeki çalıştır düğmesine basın.
Beton Sütun Tasarımı Hakkında
Sütunlar nelerdir?
Sütunlar bir binadaki dikey üyelerdir ve bir binadaki yükün temeline gitmesine izin vermenin anahtarıdır.. Dikey üyeler olarak, Öncelikle yerçekimi kuvvetleri nedeniyle büyük sıkıştırma yükleriyle uğraşırlar, ancak doğal olarak yüklemedeki eksantriklikler ve rüzgar ve deprem yükleri gibi yanal kuvvetler nedeniyle bükülme momentlerine direnmeleri gerekir.. Yığınların burkulmaya karşı kısıtlanmasına yardımcı olacak toprağa sahip olması dışında, sütunlar yığınlara oldukça benzer ve bir sütun olarak tabanında kuvvetlere direnen yığının şaftı boyunca kuvvetleri çözebilir.. Kazıklar neredeyse her zaman dairesel bir bölüme sahiptir, ancak beton sütunlar genellikle dairesel veya dikdörtgen kesitlere sahiptir.
Neden beton sütunlar kullanıyor?
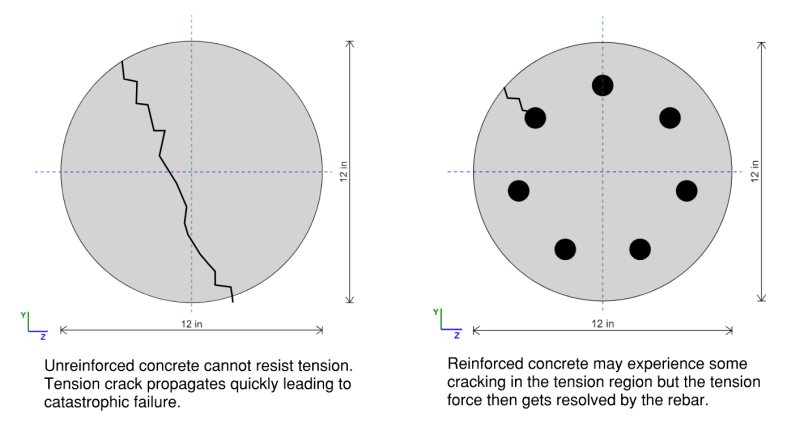
Sütunlar, doğal olarak beton kullanmak istememizi sağlayan büyük sıkıştırma kuvvetlerine maruz kalır, Sıkıştırma yükleriyle uğraşmak için çok ekonomik bir çözüm. ne yazık ki, Düz beton kırılgan ve gerginlik ve bükülme, çelik takviye çubukları olmadan kullanılmasını güvensiz hale getirir (inşaat demiri).
Betonarme sütunlar, ekonomik bir sütun tasarımı için betonun sıkıştırma mukavemetini ve inşaat demiri gerilim mukavemetini kullanır. Beton sütunlar, dayanıklılıkları nedeniyle inşaatta yaygın olarak kullanılmaktadır., yangın direnci, ve ağır yükleri destekleme yeteneği.
Betonarme sütunlar için nasıl tasarlanır
Güçlendirilmiş bir sütunun kompozit doğası, ilk prensiplerden analiz etmeyi zorlaştırır. Çelikle, bölüm modülünü hesaplayabilir ve bir bükülme kapasitesi bulmak için akma mukavemetiyle çarpabiliriz.. Betonarme ile bölüm homojen değildir ve iki farklı malzeme ile neyin olduğunu ve bölümümüzün nasıl başarısız olabileceğini gerçekten görmek için stres-suş grafiğine bakmamız gerekir..
Sütunların neredeyse her zaman aynı anda hareket eden bükme ve sıkıştırma kuvvetlerine sahip olduğunu düşündüğümüzde bu zorlaşıyor, bu da sütunun kapasitesini etkiliyor. Böyle bir tasarıma yardımcı olacak bir araç, etkileşim diyagramı olarak bilinen şeydir.
Etkileşim diyagramı nedir ?
Bir etkileşim diyagramı.
Bu makalenin aşağıdaki bölümleri, güçlendirilmiş bir sütun için etkileşim diyagramının elle nasıl hesaplanacağı açıklanacaktır.. Etkileşim diyagramını oluşturma prensiplerini takiben, okuyucuyu bir etkileşim diyagramındaki anahtar noktaları daha iyi anlayarak ve beton bir sütun tasarımı için etkileşim diyagramının sonuçlarının nasıl yorumlanacağı ile bırakacaktır..
Her sütun bölümü için elle bir etkileşim diyagramı oluşturmak zaman alıcı olabilir, bu nedenle beton sütunlar için etkileşim diyagramları oluşturmak ve ayrıca bir kullanıcının etkileşim diyagramını manuel olarak kontrol etmesini gerektirmeden tasarım yüklerine dayalı olarak kullanımı değerlendirmek için SkyCiv Beton Sütun Hesaplayıcısı gibi yazılımlar mevcuttur..
Bir etkileşim diyagramı nasıl oluşturulur
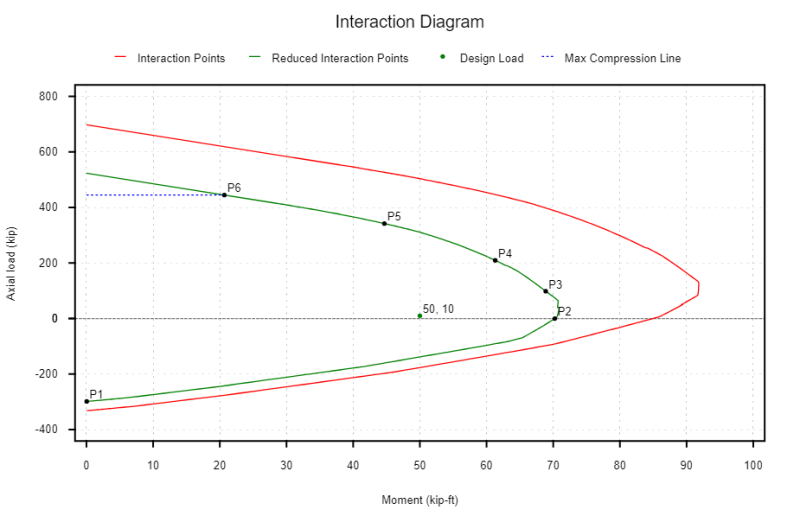
Bir etkileşim diyagramı oluşturmak, aşağıdaki durumlar için betonarme kolonunun değerlendirilmesini içerir:
- (kilo kaybı hikayeleri.net) Saf gerilim - Bu, kolonun destekleyebileceği en büyük eksenel gerilim yüküdür..
- (kilo kaybı hikayeleri.net) Saf bükülme - Bölüm bükülme momentine ve p = eksenel kuvvetine tabidir. 0
- (P3) Dengeli nokta (et = ety) - Beton arızası, aşırı gerilme çelik verimiyle aynı zamanda gerçekleştiğinde dengeli bir duruma ulaşılır..
- (P4) Yarım verimli nokta (et = 0.5 ety) - Bu, doğru bir etkileşim diyagramının çizilmesine yardımcı olacak bir ara konumdur.
- (P5) Dekompresyon noktası (et = 0) - Bu durum, gerginlik tur ekleri sıkıştırma tur eklerine değiştiğinde konumu işaretler (ACI). Çubuklar sadece gerginlik kuvvetleri almak arasında sadece sıkıştırma kuvvetleri almaya geçiyor.
- (P6) Saf sıkıştırma - Bu, kolonun destekleyebileceği en büyük eksenel sıkıştırma yüküdür..
Etkileşim diyagramımız, tasarımımızda gereken güvenlik azaltma faktörünü de göz önünde bulundurabilir.. Yukarıdaki etkileşim diyagramında fark edebileceğimiz bir şey, sıkıştırma kontrollü bölgede daha büyük bir güvenlik faktörüne sahip olmamızdır. (0.65 veya 0.75) gerginlik kontrollü bölgede yaptığımızdan (0.9).
ACI'ye göre beton sütun tasarımı için indirgeme faktörleri 318-19
Güç azaltma faktörü (hesaplamalar ayrıca açık ve ayrıntılı PDF raporlama ile birlikte gelir) şu an için kullanılır, Eksenel kuvvet veya kombine moment ve eksenel kuvvet, bölümün nasıl sınıflandırıldığına bağlıdır.
Bölüm, net gerilme suşuna göre sınıflandırılmıştır (et) gerginlik yüzüne en yakın takviyedeki zorlama:
- Gerilim kontrollü : et ≥ ety + 0.003
- Geçiş : ety < et < ety + 0.003
- Sıkıştırma kontrollü εt <= ety
Güç azaltma faktöründeki değişiklik nedeniyle, sıkıştırma kontrol noktasını elle hesaplamak da yararlı olabilir. (Önceki diyagramda P3) ve gerilim kontrol noktası (et ≥ ety + 0.003) etiketlenmemiş.
Aynı zamanda enine takviyemize de bağlıdır. Onaylayan spiraller için 25.7.3 phi'yi ε alabiliriz.t gibi:
- Gerilim kontrollü: Φ = 0.9
- Sıkıştırma kontrollü: Φ = 0.75
- Geçiş: Φ = 0.75 + 0.15 (et - ety ) / 0.003
Diğer enine takviye türleri için:
- Gerilim kontrollü - Φ = 0.9
- Sıkıştırma kontrollü - Φ = 0.65
- Geçiş = φ = 0.65 + 0.25 (et - ety ) / 0.003
(Aslında geçiş formülü, sıkıştırma veya gerilim kontrol noktasına ne kadar yakın olduğumuza bağlı olan basit bir doğrusal fonksiyondur.)
Bir beton sütunun saf sıkıştırma kapasitesinin nasıl hesaplanması
Saf sıkıştırma kapasitesi veya kabak yükü, saf eksenel yükleme altındaki kolonun gücüdür.
ACI'yi kullanmak 318-19 Bölüm 22.4.2 Aşağıdaki formülü kullanarak beton bir sütun için saf sıkıştırma yükünü hesaplayabiliriz:
P0 = 0.85 f'c * (Birg - BirAziz) + fY * BirAziz
nerede:
- f'c somut sıkıştırma mukavemeti
- fY inşaat demiri verim gücüdür
- Birg bölümün brüt alanıdır
- BirAziz çelik inşaat demerinin toplam alanı
- (Birg - BirAziz) betonun etkili kesit alanıdır.
Bu nokta, bir mukavemet azaltma faktörü uygulanmadan etkileşim diyagramının en soluna karşılık gelir. Sıkıştırma kontrollü bölge için bu değeri güç azaltma faktörümüzle azaltabiliriz (Saf kompresyonda olduğumuz için kesinlikle sıkıştırma kontrollü bölgedeyiz). ACI 318-19 Ancak, kesik mavi çizgi tarafından verilen ve bir sonraki bölümde kapsanan bunun ötesinde maksimum bir sınır getirir.
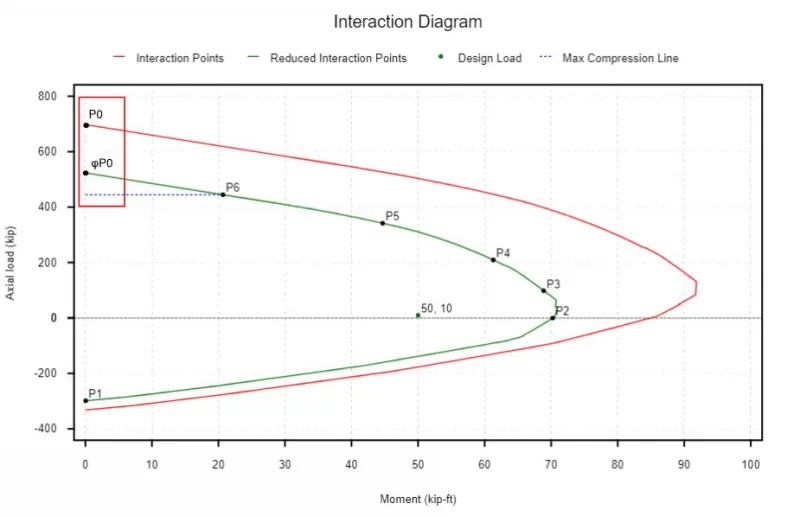
Bir beton sütunun izin verilen maksimum sıkıştırma kapasitesinin nasıl hesaplanması (ACI)
Kazara eksantrikliği hesaba katmak için 318-19 Bir betonarme kolonun izin verilen maksimum sıkıştırma bileşiğini sınırlar. 80 -e 85 Önceki bölümde hesaplanan saf nominal sıkıştırma kapasitesinin yüzdesi.
Azaltma, üye türüne ve sütunda kullanılan enine takviyeye bağlıdır (Masa bakın 22.4.2.1 ACI 318-19).
Genellikle enine takviyenin bağlar olduğu aşağıdakilere sahibiz:
- Pn,max = 0.80 * P0
Veya enine takviye spirallerse:
- Pn,max = 0.85 * P0
Bir beton sütunun saf gerilim kapasitesinin nasıl hesaplanması (ACI)
Betonarme sütunun gerilim mukavemeti tamamen takviyenin gücünden gelir ve sahip olduğumuz takviye alanıyla orantılıdır..
Bir betonarme sütunun eksenel gerilim mukavemetini hesaplama formülü basitçe:
Pnt,max = fY * BirAziz
&
P1 = φ * Pnt,max
Bölüm saf gerginlikte olduğundan ve tüm çubuklarımızın verildiği düşünüldüğü için bölüm gerginlik kontrol edilir ve mukavemet azaltma faktörü φ her zaman 0.9.
Bir beton sütunun bakiye noktası kapasitesinin nasıl hesaplanması
Denge noktası, aşırı gerginlik üyesinin ilk verimine neden olan yükleme olarak tanımlanır.t = ety Aynı anda betonun verilmesi. Sütun mukavemetini hesaplamak için kullanılan yöntem (Esneme ve eksenel sıkıştırma veya gerilim için) Bu noktada, belirli bir ε ile diğer noktalar için kullanılan yöntemle aynıdır.t (yani. εT = 0, et = 0.5 εty).
Önce takviyenin verim zorluğunu Hookes yasasını kullanarak hesaplayabiliriz:
εty = fY / E
için 60 bir genç modülü ile KSI bar 29000 KSI Bir verim zorluğumuz var
εty = 60/290000 = 0.00207
Ayrıca her zaman betonun verim zorluğunu alırız 0.003 (Bölümde tanımlanmış 22.2.2.1 ACI 318-19).
Bu iki değeri kullanarak gerinim diyagramımızı çizebiliriz ve gerinim diyagramına dayanarak bölümümüzdeki stresleri belirleyebiliriz.. Streslerin hesaplanması sonraki iki bölümde ele alınmıştır..
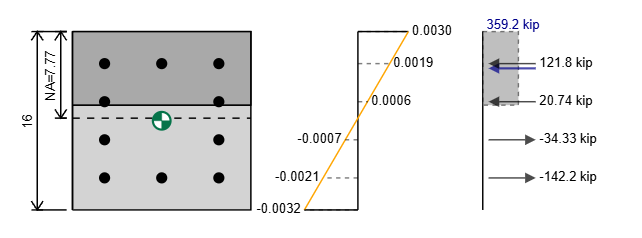
Beton sütundaki takviye kuvveti nasıl hesaplanır
Takviyedeki stres ve kuvvetin hesaplanması, saf gerilim gücünü nasıl hesapladığımıza benzer. Stresimiz, gençliğimizin modülünü zorlamalarımızla eşittir, ancak verim stresi ile sınırlıdır.
σ = Min( et * E , ety * E )
Daha sonra, bu sıradaki çubukların alanı ile stresi çarparak çubuklarımızdaki kuvveti belirleyebiliriz.. Aynı suşa sahip birden fazla çubuğumuzun olduğu hesaplamaları basitleştirmek için bunları birlikte gruplayabiliriz.
Ft = σ * Bir
Sıkıştırma veya gerginlikte olan gücümüzü ayırt etmek için bir yola ihtiyacımız var. FT ve FC'yi farklı kuvvetleri belirtmek için kullanabiliriz, ancak bu örnek için ve SkyCiv Hesap Makinesi'nde, gerginliği ve pozitif temsil eden sıkıştırmayı temsil eden bir işaret gösterimi kullanacağız..
Somut bir stres bloğu üzerindeki kuvvet nasıl hesaplanır
Betonlu bir bölümün beton bileşenimizin beton bileşenindeki stresin hesaplanması biraz daha karmaşıktır, çünkü beton bir bölüm için stres dağılımı doğrusal değildir ve bunun yerine yaklaşık paraboliktir.. neyse ki, Whitney stres bloğu yöntemi olarak bilinen somut bölümde streslerin hesaplanması için ampirik bir basitleştirme vardır.. Bu yöntemde, dikdörtgen bir stres bloğu olarak parabolik stres dağılımını yaklaşık.
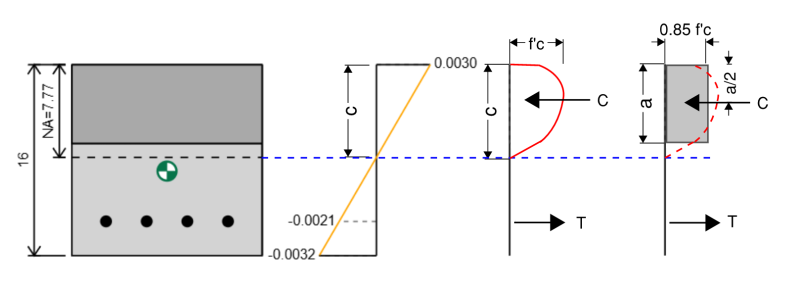
ACI bu yöntemi bölümdeki açıklar 22.2.2.4.1. A'yı hesaplıyoruz:
A = B1 * c
β1 nereden değişir 0.65 -e 0.85 Sıkıştırma gücüne bağlı olarak (f'c) beton (Masa bakın 22.2.2.4.3).
Stres bloğundaki kuvveti hesapladığımızda, her zaman etkili bir stres kullanırız 0.85 * f'c.
Böylece sıkıştırma kuvvetini şu şekilde hesaplayabiliriz:
FC = 0.85 * f'c * B1 * c
ve kuvvet, aşırı sıkıştırma kenarından A/2 pozisyonunda hareket eder.
Bir stres-gerinim diyagramından bir beton kolonun eksenel kapasitesi nasıl hesaplanır
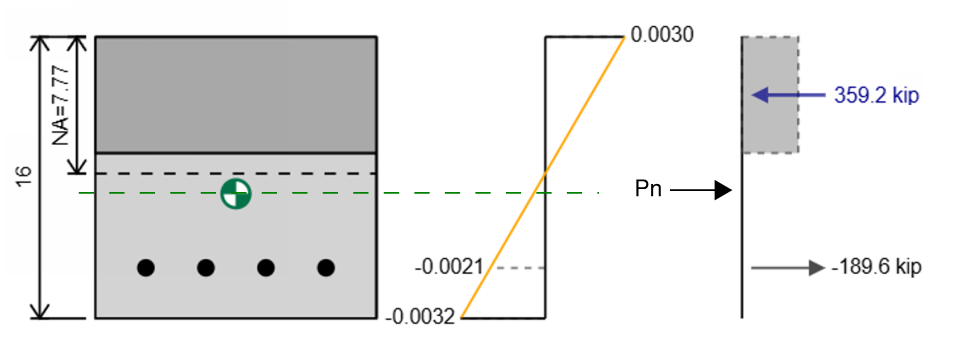
Şimdi tüm suşlara sahibiz, Bölümümüzde takviye ve beton üzerindeki stres ve kuvvetler, ancak yine de bu bölüm için eksenel kapasite veya bükülme kapasitesinin ne olduğunu belirtmedik..
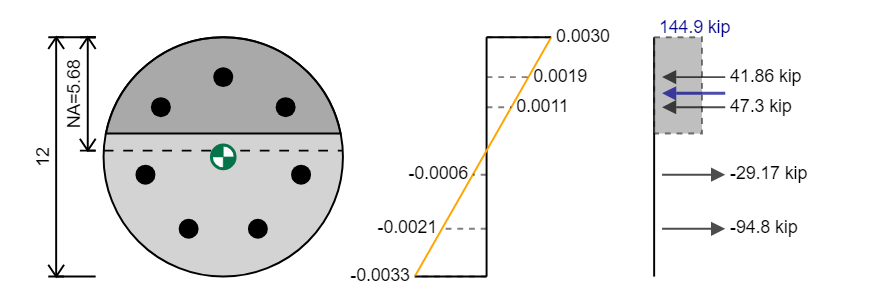
Eksenel kapasite sonuçta ortaya çıkan kuvvettir ve hareket ettiği pozisyon plastik sentroiddir (Diyagramda yeşil sentroid işaretleyici). Yukarıdaki örnekte eksenel kapasite
Princi KullanmaStatics Ples Bölümümüzün kapasitesini belirlemek için kuvvet diyagramımızı kullanabiliriz.. İlk olarak eksenel kapasiteyi belirlemek için kuvvetlerin toplamını kullanabiliriz, Toplam sıkıştırma kuvvetlerimizin toplam gerginliğimize eşit olması gerektiğini bilmekbunlar.
Σfx = 0 → σc = σt
Daha sonra, bölümümüzün eksenel kapasitesi olan sonuç kuvvetini bulmak için çelik sıkıştırma kuvvetlerini ve beton basınç kuvvetini ve çelik gerilim kuvvetlerini toplamayabiliriz..
PN = σc - Σt
Örneğin, varsa 359.2 Sıkıştırma Kip ve 189.6 gerginlik kip Bölüm için sonuçta ortaya çıkan kuvvet 359.2 - 189.6 = 169.6 kip. Bölümü tamamen dengeleyecek olan kuvvetin (yani gerilim kuvveti 169.6) kapasitenin tam tersi 169.6 yapabildiğimiz için sıkıştırmada kip
Bir stres-gerinim diyagramından bir beton kolonun bükülme kapasitesinin nasıl hesaplanması
Artık onu dengelemek için bölümümüzde hareket eden bir kuvvete ihtiyacımız olduğunu biliyoruz. Bu kuvvet, yukarıdaki çizimde yeşil sentroid işaretleyici ile işaretlenen bölümün plastik sentroidinde hareket eder..
Plastik centroid'i bulmak için hesaplamalar bir Normal sentroid hesaplaması Bir mesafe ile çarpmak yerine, birden fazla f mesafe.
Eğilme kapasitesini hesaplamak için herhangi bir pozisyonla ilgili anlar alabiliriz ve net bir an elde edeceğiz. Plastik sentroidin pozisyonu hakkında anları alabiliriz, bu yüzden kolu olacağı için hesaplamalarımızdaki PN kuvveti hakkında endişelenmemize gerek yoktur. 0. Bir tablo bu hesaplamalar için özellikle birçok takviye katmanımız olduğunda.

Moment kapasitemiz için hesaplamaların
MN = Σf x kolu = 359.2 x 5.615/12 + -189.6 x -4.206/12 = 168.1 + 66.5 = 234.6 acı
Olumlu bir an, bölümün üstünün sıkıştırma içinde olduğunu ve bölümün alt kısmının gergin olduğunu gösterir.
Beton sütununun azaltılmış bükülme ve eksenel kapasitesi nasıl hesaplanır
Bir an kapasitesini hesapladık 234.6 Kip-ft ve sıkıştırma kapasitesi 169.6 KIP Ancak bunlar nihai kapasitelerimizdir ve bir mukavemet azaltma faktörü phi ile azaltılması gerekir.
Şu anda denge noktasını düşünüyoruz ve εt = εty var, o zaman sıkıştırma kontrollü bölgedeyiz ve bir güvenlik faktörünü kullanmalıyız 0.65 veya 0.75 Betonarme sütundaki enine takviyeye bağlı olarak.
Bir etkileşim diyagramı çizmek
Şimdiye kadar nasıl hesaplanacağını gördük
- (kilo kaybı hikayeleri.net) Saf gerilim noktası
- (P6) Saf sıkıştırma noktası
- (P3) Dengeli nokta
Dengeli nokta için hesaplama ile aynı prosedürü kullanarak, eksenel ve eğilme kapasitesini de hesaplayabiliriz.:
- (P4) Yarım verimli nokta
- (P5) Dekompresyon noktası
Bu üç nokta arasındaki fark (P3, P4, P5) sadece aynı olmasını takip eden her adımda gerinim diyagramı üretirken yaptığımız ilk varsayımdır..
Bu beş nokta ile hesaplamadığımız tek nokta saf bükülme noktasıdır. Bu nokta, pn = sahip olduğumuz noktaya karşılık gelir. 0 Bölümümüzde. Bu noktayı belirlemek için nötr eksen pozisyonunu tahmin ettiğimiz yinelemeli bir çözüme ihtiyacımız var (ACI'de C değeri) ve pn = olup olmadığını belirleyin 0. Nötr eksenin bu konumunu bulduktan sonra, denge noktası için yaptığımız gibi adımlarımıza devam edebiliriz..
Belirlenen her değerle, betonarme sütunumuz için bir etkileşim diyagramı oluşturabiliriz. Basit bir etkileşim diyagramı oluşturmak için kilit noktalarımızı çizebilir ve aralarında düz bir çizgi çizebiliriz. Skyciv Quick Design Beton Sütun Hesap Makinesi gibi yazılımlarla etkileşim diyagramında, daha yumuşak ve daha doğru bir arsa olarak verebilecek kilit noktalardan ziyade daha fazla puan oluşturabiliriz..
ACI'ye tasarım yaparken çizilmesi yararlı olabilecek başka bir nokta 318-19 gerginlik kontrol geçiş noktasıdır, çünkü phi faktörünün tıpkı p3 pozisyonunda olduğu gibi değişmeye başladığı yerdir, bu da sıkıştırma kontrol geçiş noktasıdır. Ayrıca, izin verilen maksimum saf sıkıştırma kuvvetinde bir azalma olduğu için (mavi çizgi ile gösterilir) Maksimum sıkıştırma kuvveti, aşağıdaki grafikte P6 Noktası tarafından belirtilen bazı moment kapasitesine direnebilir..
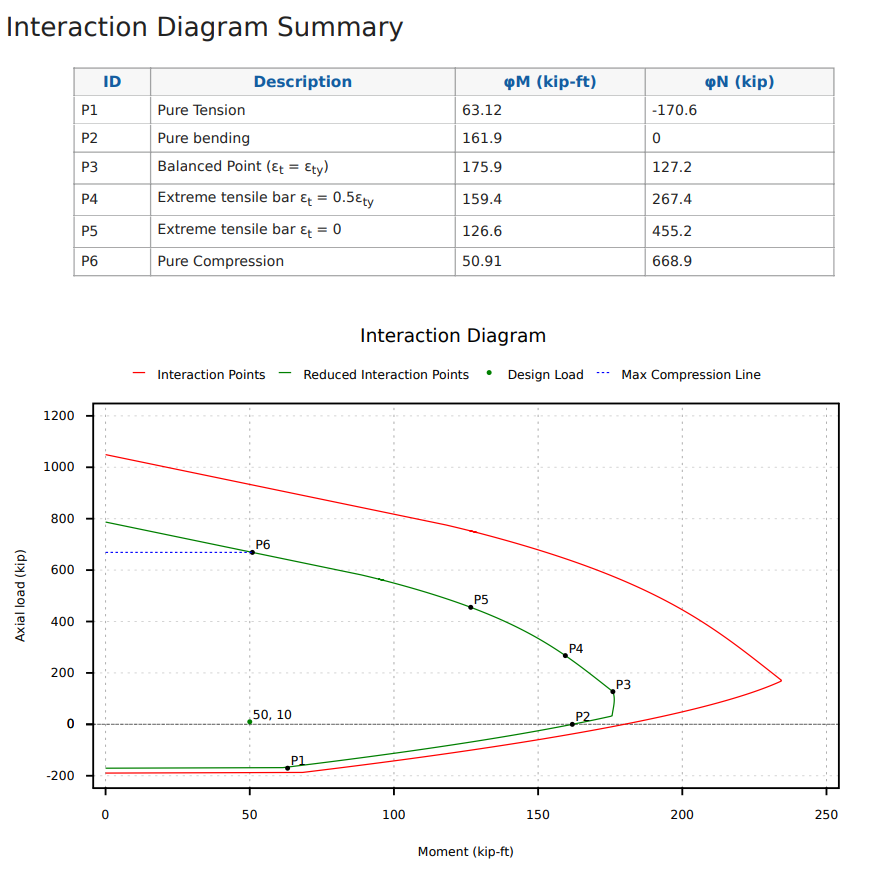
Bir etkileşim diyagramı nasıl okunur?
Şimdiye kadar bir etkileşim diyagramının nasıl oluşturulacağı hakkında çok şey öğrendik, ancak tasarımımızda nasıl kullanabiliriz ve neden gerekli.
sonuçta, Etkileşim diyagramı yararlıdır çünkü bölümümüz için her zaman aynı (Belli bir yönde bükülürken) ve eksenel gücümüzün ve momentimizin varyasyonlarına bağlı değil.
Sadece bölümümüzün tek bir eksenel kuvvet ve moment kombinasyonu kapasitesine sahip olup olmadığını hesaplayacak olsaydık, diyagrama ihtiyacımız olmayabilir, ancak dikkate almak istediğimiz birden fazla farklı yük kombinasyonumuz ve kuvvetimiz varsa çok tekrarlayan hesaplamalar yapar..
Etkileşim diyagramı, belirli bir yük kombinasyonunun ACI gibi kullandığımız tasarım standardının gereksinimlerini karşılayıp karşılamadığını hızlı bir şekilde belirlememizi sağlayan görsel bir araçla kullanım sağlar. 318-19. Tek yapmamız gereken bizim amacımızı çizmek ve bunun etkileşim diyagramımızın alanında olduğundan emin olmaktır., Ve aynı anda birçok farklı yük kombinasyonunu çizebiliriz.
Kullanım oranları biraz keyfidir, çünkü çoğunlukla bölgenin içindeyiz ya da değiliz, Ancak kullanım oranlarını belirli bir sınırdan ne kadar uzakta olduğumuza göre tanımlayabiliriz. X eksenindeki mesafemiz, etkileşim diyagramı için moment kullanımımızdır ve y eksenindeki mesafemiz, etkileşim diyagramı için eksenel kullanımımızdır.
Beton bir sütun üzerinde iki eksenli bükme için bir etkileşim diyagramı nasıl oluşturulur
Daha önce baktığımız etkileşim şeması, dikdörtgen betonarme bölümünün tek eksenli bükülmesi içindi. Sadece bir eksen yaklaşık olarak bükülmenin olduğunu düşündük, ancak aynı zamanda küçük eksen bükülebiliriz. Küçük eksen bükme için, bölümü döndürmemiz dışında her şeyi aynı yapardık 90 Dereceler, bunun yerine böyle bir şeyimiz olur.
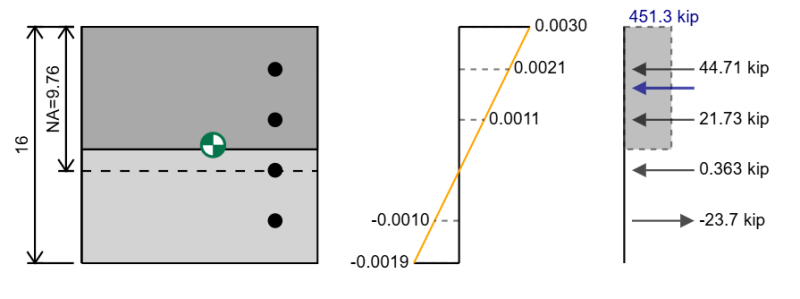
İki eksenli bükülme için bölümümüzü, sonuçta ortaya çıkan anın düzlemi hakkında bükecek şekilde döndürmemiz gerekir.. Bu iki eksenli diyagram için alacağımız etkileşim diyagramı, sadece bu özel momentin yönü için geçerlidir..
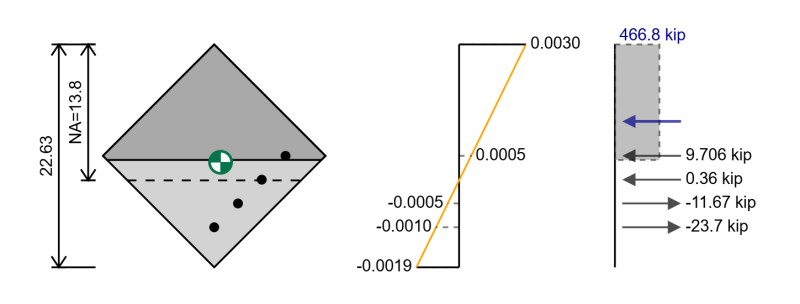
Daha önce etkileşim diyagramı için yaptığımız aynı adımları izleyebiliriz, ancak şimdi takviyemiz için farklı pozisyonlarımız olacak ve iki eksenli bükülmede dikdörtgen bir bölüm durumunda, sıkıştırmada olan üçgen bir alana sahibiz..
Beton sıkıştırma kuvvetini şu şekilde hesaplamak yerine:
FC = 0.85 * f'c * B1 * c
Bunun yerine beton sıkıştırma kuvvetini şu şekilde hesaplayabiliriz.:
FC = 0.85 * f'c * Bir
burada A, A = β1 konumunun üzerindeki sıkıştırma alandır * c
3D etkileşim diyagramı nedir?
İki eksenli bükülme için 2D etkileşim diyagramı oluşturmanın sınırlamalarından biri. Şimdi kapasitemizi göz önünde bulundurarak üç değişkenimiz var, neden MZ, Benim ve n. Doğal olarak, sadece iki ekseni işleyebilen bir 2D grafik ve dolayısıyla iki değişken kullanmak yerine, üç değişkeni işleyebilen üç boyutlu bir etkileşim diyagramı oluşturabiliriz.
2D etkileşim diyagramı gibi, hedefimiz de grafik alanının içindeki yük kombinasyonlarımızın olması, farkın dikkate alınması gereken üç noktamız olmasıdır. (Mz, Aşağıdaki kaydırıcı ile bu yüzeyleri oluşturan tüm eğrileri kontrol edebilirsiniz.,N) Ve amacımızın etkileşim diyagramı hacmimizde bulunması gerekiyor (alandan ziyade). Bu, aynı anda birden fazla noktayı değerlendirmek için yararlı bir görsel araçtır, ancak sınırlaması, statik grafikler veya görüntüler gibi 2D ortamlarda kullanmanın zor olması ve böyle bir grafiği tam olarak kullanmak için etkileşimli bir yazılım gerekli olmasıdır.. SkyCiv Bölüm Builder, çalışması kolay olan 3D etkileşim diyagramlarının üretilmesine yardımcı olabilir..
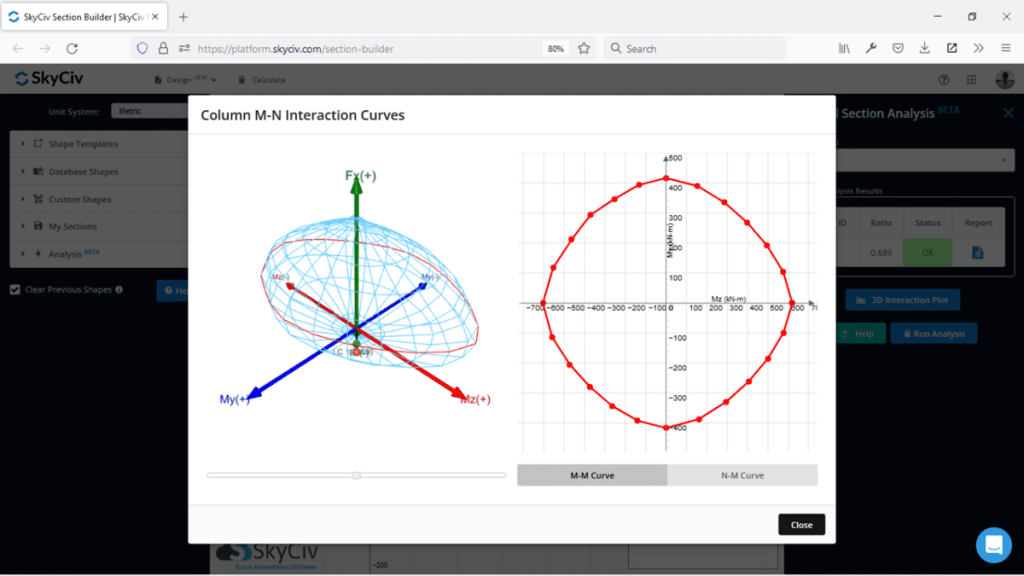
3D etkileşim diyagramı nasıl oluşturulur
Tüm veri noktalarını elde etmek için bir 3D etkileşim diyagramı oluşturmamız gerekiyor, daha önce yaptığımız aynı 2D değerlendirmeyi yapıyoruz, ancak bölümü yavaş yavaş döndürdüğümüz için bunu birden çok kez yapıyoruz. Sevdiğimiz rotasyonu kullanabiliriz, Makul bir açı olabilir 15 bize verecek dereceler 24 Farklı Açılar.
Verileri elle almak sıkıcıdır ancak mümkündür, ancak bu verileri 3D etkileşimli etkileşim diyagramı oluşturmak için kullanmak son derece zordur. 3D Etkileşim diyagramları en iyi SkyCiv Bölüm Oluşturucu gibi yazılımlarla kullanılır.
İlgili Araçlar
SkyCiv hakkında
SkyCiv, mühendisler için çok çeşitli Bulut Yapısal Analiz ve Tasarım Yazılımı sunar. Sürekli gelişen bir teknoloji şirketi olarak, Mühendislere iş süreçlerinde ve tasarımlarında zaman kazandırmak için mevcut iş akışlarını yenilemeye ve bunlara meydan okumaya kararlıyız.