Что такое P-дельта-анализ?

P-дельта-анализ - это тип анализа, который особенно важен для поперечного смещения конструкций многоэтажных зданий, испытывающих гравитационную нагрузку.. В этой статье, Программное обеспечение SkyCiv Online Engineering обсудит простую теорию, лежащую в основе эффектов P-Delta, и поможет вам понять важность такого анализа при моделировании ваших структур.

Что такое P-дельта-эффекты?

Конечно, любая структурная модель будет отклоняться при загрузке. Отклоненная конструкция может столкнуться со значительными второстепенными моментами, поскольку концы стержней изменили положение.. Чтобы проиллюстрировать это, рассмотрим простой пример консольной колонны, показанный ниже: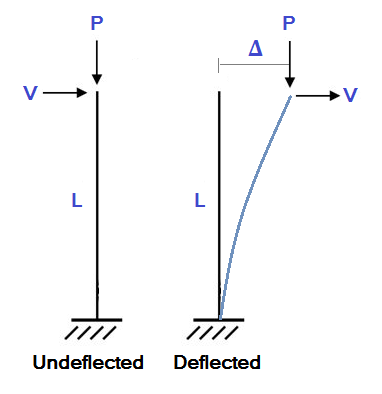

В этом примере, столб длиной L испытывает осевую нагрузку (п) и боковая нагрузка (V). В стандартном линейном статическом анализе мы рассчитали бы боковое отклонение (Δ) так как: [математический] \Дельта = dfrac{МЛ ^ 2}{3Нет} = dfrac{VL ^ 3}{3Нет} \текст{ поскольку M = VL} [математический] Обратите внимание, что в случае линейного статического анализа боковое отклонение, Δ, зависит от боковой нагрузки (V). тем не мение, если колонна испытывает осевую нагрузку (п), тогда не будет ли колонна отклоняться еще больше? Это очевидно, потому что осевая нагрузка создаст вторичный момент со значением P × Δ.. Чтобы проиллюстрировать это, подведем итоги по основанию колонны: [математический] \сумма{M}знак равно(V раз L) + (P times Delta)= VL + P Delta \\\\ M_{1} = VL \\\\ M_{2} = P Delta [математический] Здесь M₁ возникает из-за точечной боковой нагрузки, тогда как, M₂ из-за осевой нагрузки. Каждый из этих моментов по-разному способствует боковому отклонению. (вы можете найти формулы консоли для конечного прогиба из-за точечной нагрузки и момента, соответственно для этих формул): [математический] \Дельта_{1} = dfrac{M_{1}L ^ 2}{3Нет} = dfrac{VL ^ 3}{3Нет} \\\\ \Дельта_{2} = dfrac{M_{2}L ^ 2}{2Нет} = dfrac{P Delta L ^ 2}{2Нет} [математический] Серьезно, полное боковое отклонение будет ближе к: [математический] \Дельта_{новый} = Delta_{1} + \Дельта_{2} = dfrac{VL ^ 3}{3Нет} + \dfrac{P Delta L ^ 2}{2Нет} [математический] Мы видим, что по сравнению с исходным значением отклонения, справа есть дополнительный член в терминах P и Δ. Если P или Δ - значимые значения, стандартный линейный статический анализ будет недооценивать прогиб колонны. Теперь должно быть очевидно, что P-дельта-анализ назван в честь вторичного момента. PD. Следовательно, Эффекты P-Delta вызваны геометрической нелинейностью. По этой причине, P-дельта-анализ часто называют Нелинейный анализ. Правильный P-дельта-анализ будет продолжать повторять описанный выше процесс для обновления значения Δ._новый.

Когда мне нужно беспокоиться о проведении анализа P-Delta?

Хорошая новость в том, что SkyCiv Структурная 3D теперь может выполнить за вас P-дельта-анализ. Эффекты P-Delta обычно становятся преобладающими в высоких конструкциях, которые испытывают гравитационные нагрузки и боковое смещение из-за ветра или других сил.. Если боковое смещение и / или вертикальные осевые нагрузки через конструкцию значительны, Для учета нелинейностей необходимо выполнить P-дельта-анализ.. Во многих случаях, линейный статический анализ может сильно недооценивать смещение (среди других результатов) по сравнению с P-Delta (Нелинейный) Анализ. Важность нелинейного анализа P-Delta будет проиллюстрирована на примере ниже.. Высота каркаса многоэтажного дома составляет 20 метров., высотой 5 м каждый. Колонны полностью закреплены на основании с распределенными нагрузками на каждом уровне.. Дополнительно, на верхний этаж действуют вертикальные нагрузки, учитывается собственный вес, поэтому можно моделировать гравитационные нагрузки. Также есть относительно маленький боковая нагрузка, приложенная к боковой стороне конструкции.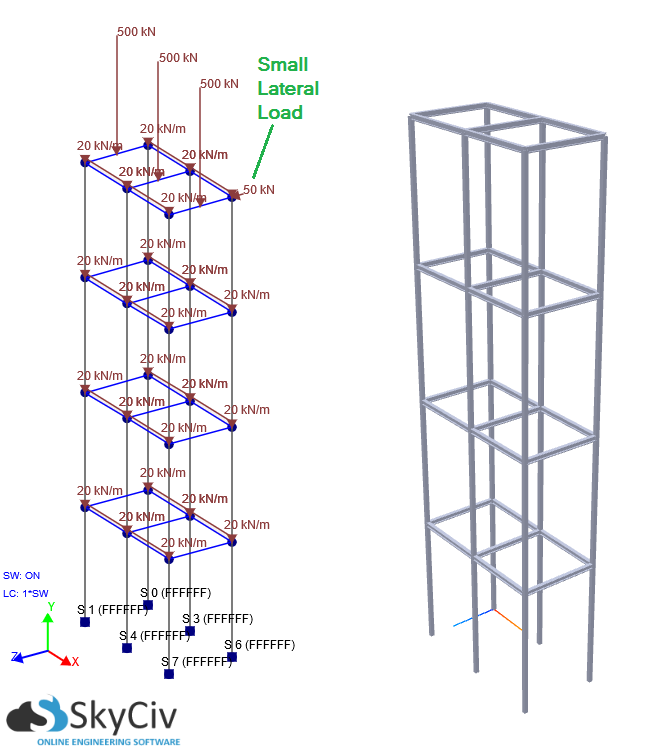

В этих условиях давайте сравним результаты между линейным и P-дельта (Нелинейный) Анализ:

	линейный	P-Delta (Нелинейный)	% Разница
Максимальное общее смещение	254 мм	353 мм	+ 39%
Максимальная вертикальная реакция	629 кН	668 кН	+ 6%
Максимальный момент реакции	42 кН-м	60 кН-м	+ 43%

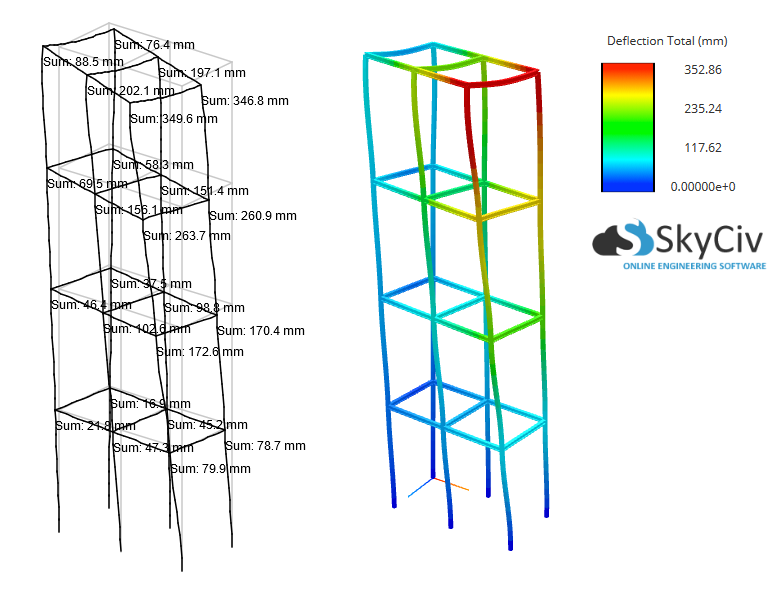Ясно, что эффекты P-Delta играют чрезвычайно важную роль в этой структуре., увеличение результатов максимального прогиба и максимального момента примерно на 40%! таким образом, линейный статический анализ в таком случае неадекватен. В итоге, P-дельта-анализ предпочтительнее линейного статического анализа, поскольку он учитывает непредвиденные нелинейности в вашей модели.. Вы можете использовать SkyCiv Структурная 3D для быстрого и эффективного анализа P-Delta на ваших моделях; просто выберите "P-дельта-анализ" при нажатии "Решить." Позвольте программе делать всю работу за вас, поэтому все, о чем вам нужно беспокоиться, - это дизайн!