Asymmetrische secties

Asymmetrische secties zijn niet symmetrisch in de verticale y-as of horizontale z-as of, in sommige gevallen, elke as. Voorbeelden van asymmetrische secties zijn hoeken en Z-secties.

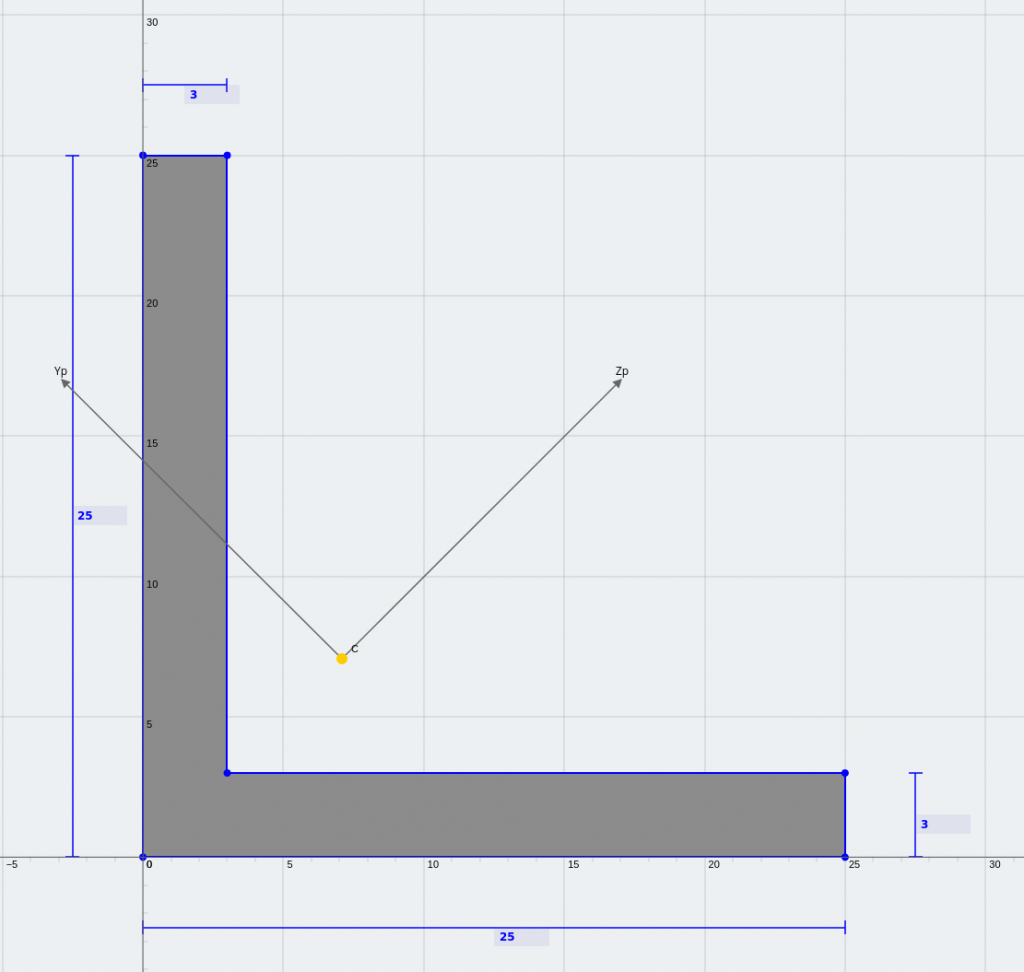
Een gelijke hoek en een Z-sectie met lip (spiegel symmetrisch om de hoofdas)

Balken met asymmetrische doorsneden gedragen zich anders dan balken met bisymmetrie bij het buigen. Zelfs als de balk een gelijkwaardige stijfheid heeft in de verticale as, zal deze zich niet gedragen als een RHS en I Shape doet dat.

In dit voorbeeld zal ik hun gedrag demonstreren met een eenvoudig belastinggeval: een verticale gelijkmatig verdeelde belasting.

Analyse

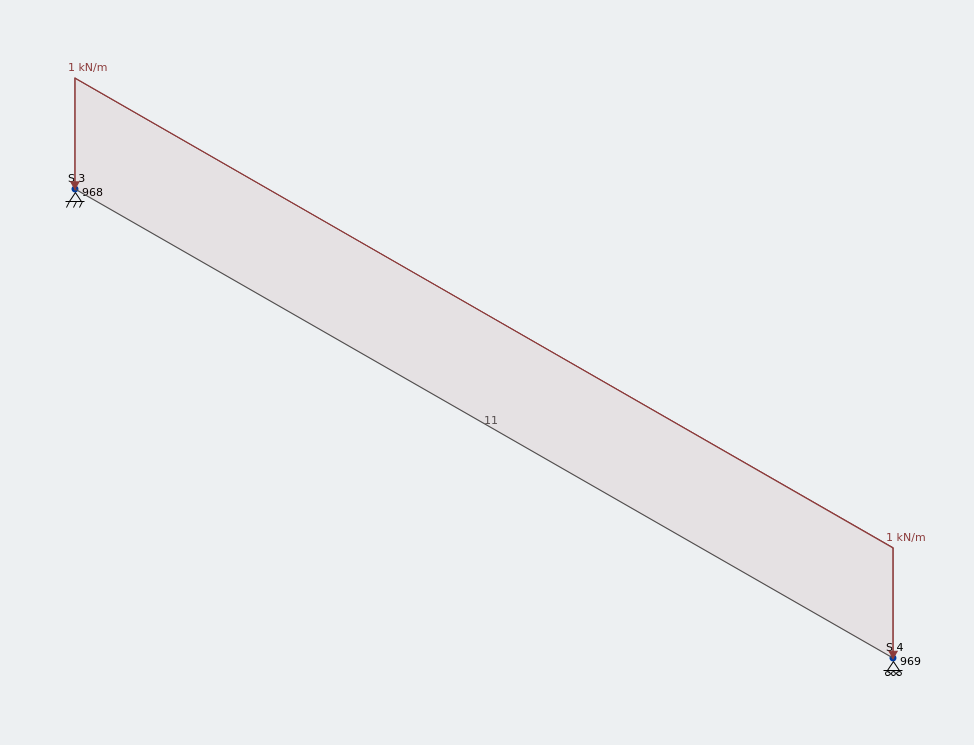
Framemodel van een 1.5 m gelijke hoek onder verticale UDL

Ik heb een gelijkmatig verdeelde belasting van 1 kN/m aangebracht over de volledige lengte hiervan 1.5 m gelijke hoek.

Als ik de doorbuiging in het midden van deze balk wilde controleren, kon ik vrij gemakkelijk. Alles wat ik nodig zou hebben zou het tweede moment van gebied zijn, en de standaard formule voor maximale doorbuiging voor een eenvoudig ondersteunde balk. Een snelle berekening met SkyCiv Section Builder en ik krijg de sectie-eigenschappen gemakkelijk.

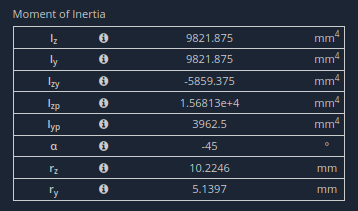
Tabel-eigenschappen van secties van SkyCiv Section Builder

Iz is 9821.9 mm tot de 4e macht. De sectie is van constructiestaal met E = 200 GPa.

Kijk wat er gebeurt als ik dit bereken met FEA in SkyCiv Structural 3D.

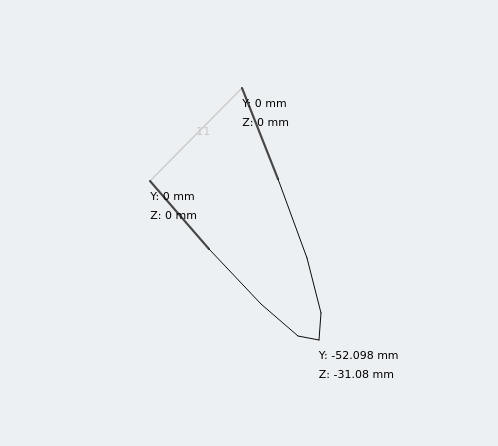
Verplaatsing van gelijke hoek onder belasting

De gelijke hoeksectie heeft twee afbuigingscomponenten! Het analyseren van de doorbuiging van een eenvoudig ondersteunde balk met behulp van een bi-symmetrische doorsnede met behulp van de vorige berekening zou dit een perfect acceptabele benadering zijn voor een snelle controle. Maar voor asymmetrische secties hebben we nog een stukje informatie nodig.

De hoek

Merk op dat in de sectie eigenschappen hierboven, de waarde voor α is niet nul.

Dit betekent dat de hoofdas niet evenwijdig is aan een van de geometrische assen.

Om het effect van het roteren van de as op de berekende stijfheidswaarden te demonstreren, Ik heb onder de stijfheid in de horizontale en verticale as uitgezet terwijl het coördinatensysteem wordt geroteerd.

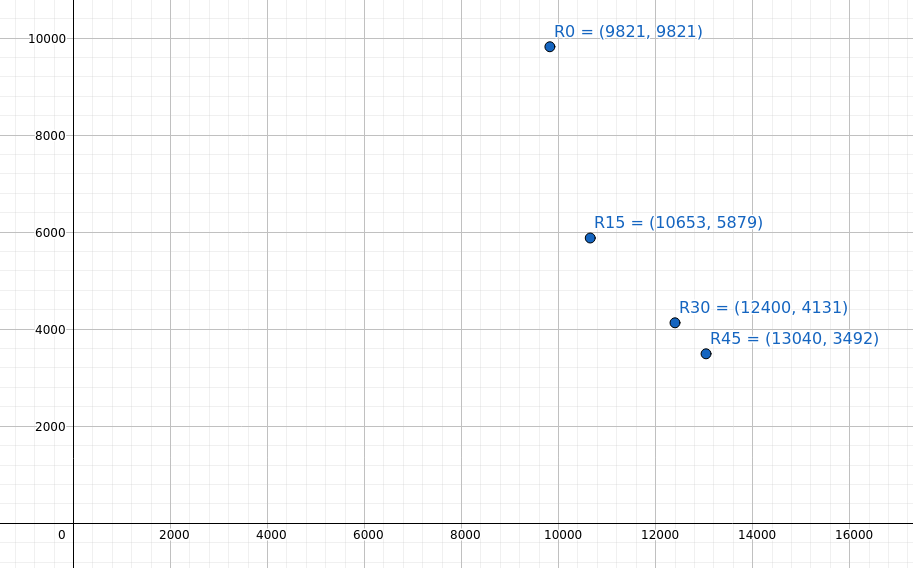
Stijfheid van 25x25x3 EA na draaien van het coördinatensysteem

Let op de niet-lineaire curve die wordt gevormd terwijl het coördinatensysteem door roteert 15, 30 en 45 graden. Deze curve is uniek voor de sectie.

Dus waarom gebeurt dit??

Een docent vertelde me eens dat belastingen de stijfste delen van de constructie volgen. In dit geval, de last wordt gedragen door de stijfste as (de grote hoofdas).

De juiste aanpak

De juiste manier om de doorbuigingsresultaten te berekenen, is door eerst alle belastingen in de hoofdassen te transformeren, vervolgens doorbuigingen berekenen op basis van het tweede gebiedsmoment langs de hoofdassen. Om te bewijzen dat dit inderdaad de juiste aanpak is, heb ik het antwoord gevalideerd met een handberekening, en om dit een beetje interessanter te maken, met een model van de balk met behulp van een frame-element en, een model opgebouwd uit schelpen. Op die manier kan er geen twijfel over bestaan ​​dat de verplaatsingen die we eerder zagen inderdaad correct zijn.

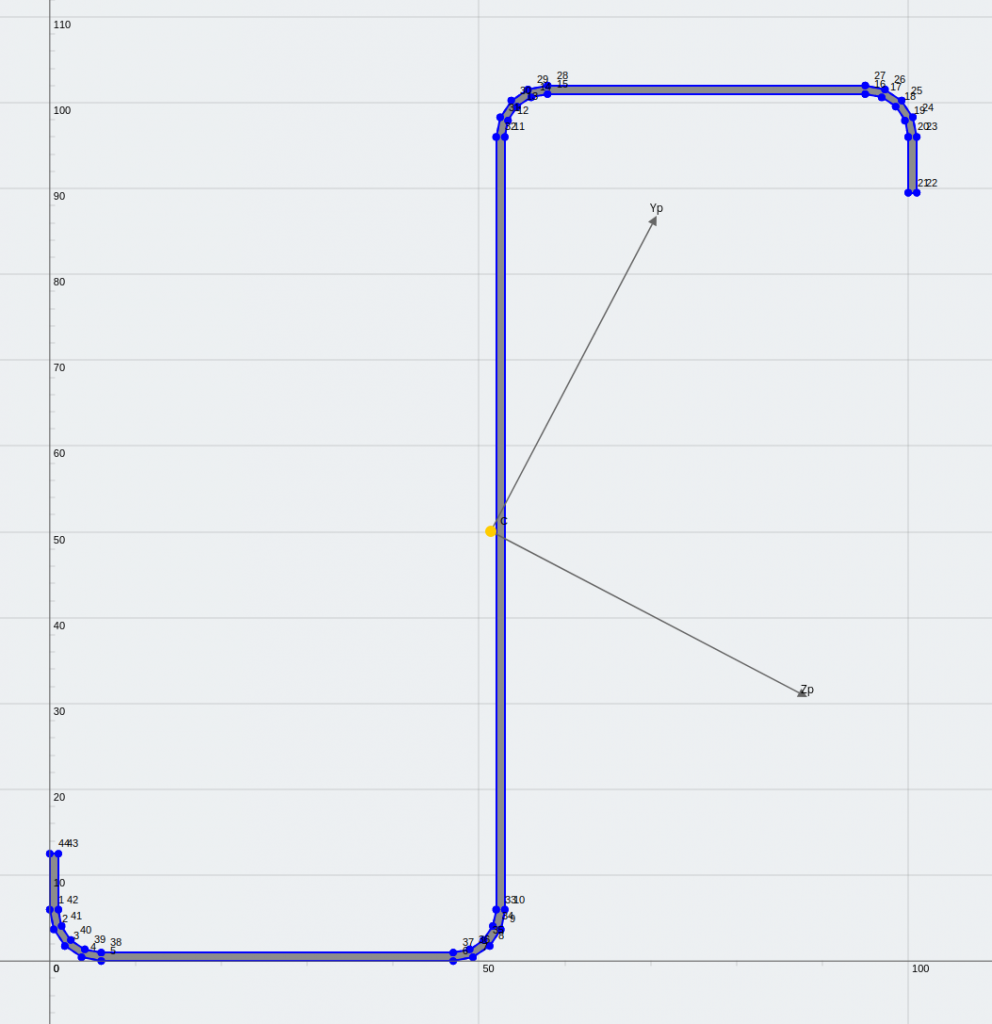
Hier is het model dat ik heb gemaakt.

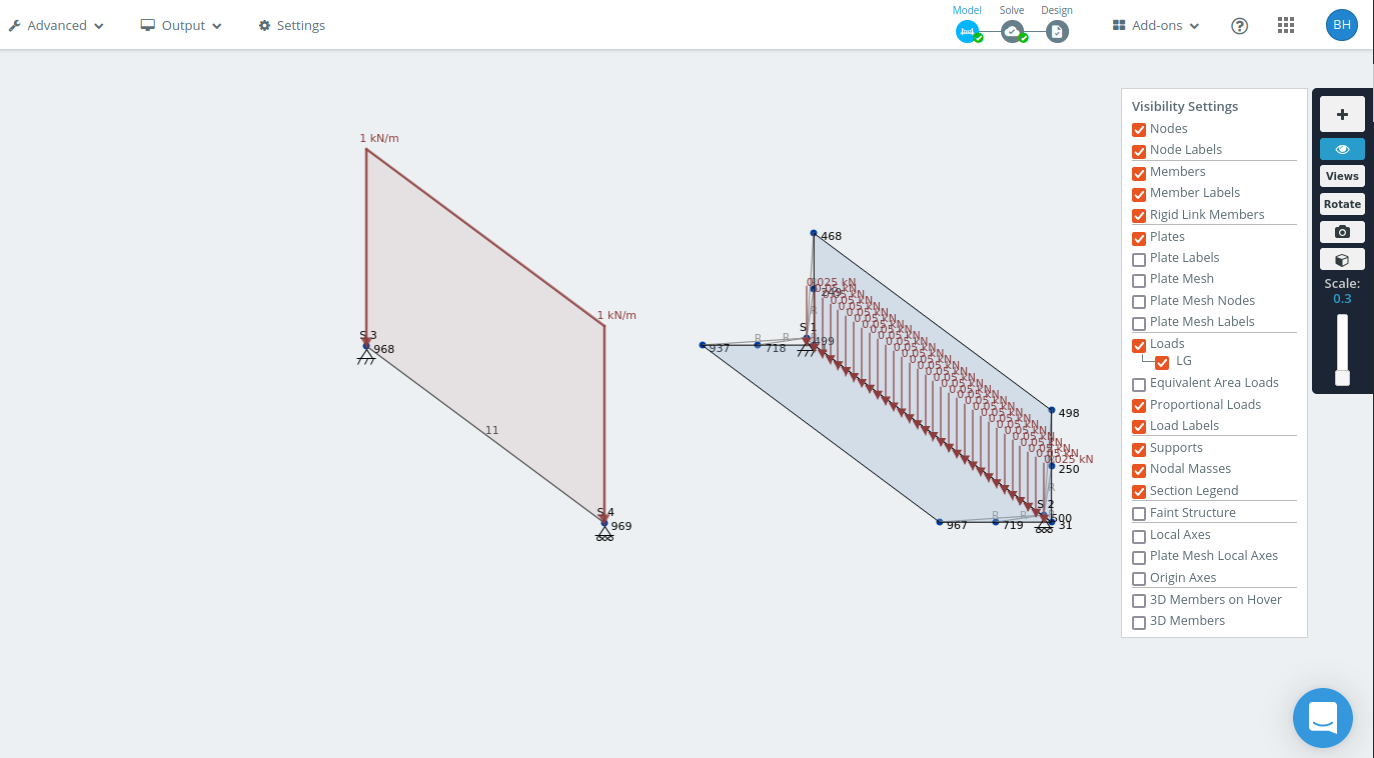
Framemodel en schaalmodel van 1.5 m hoek

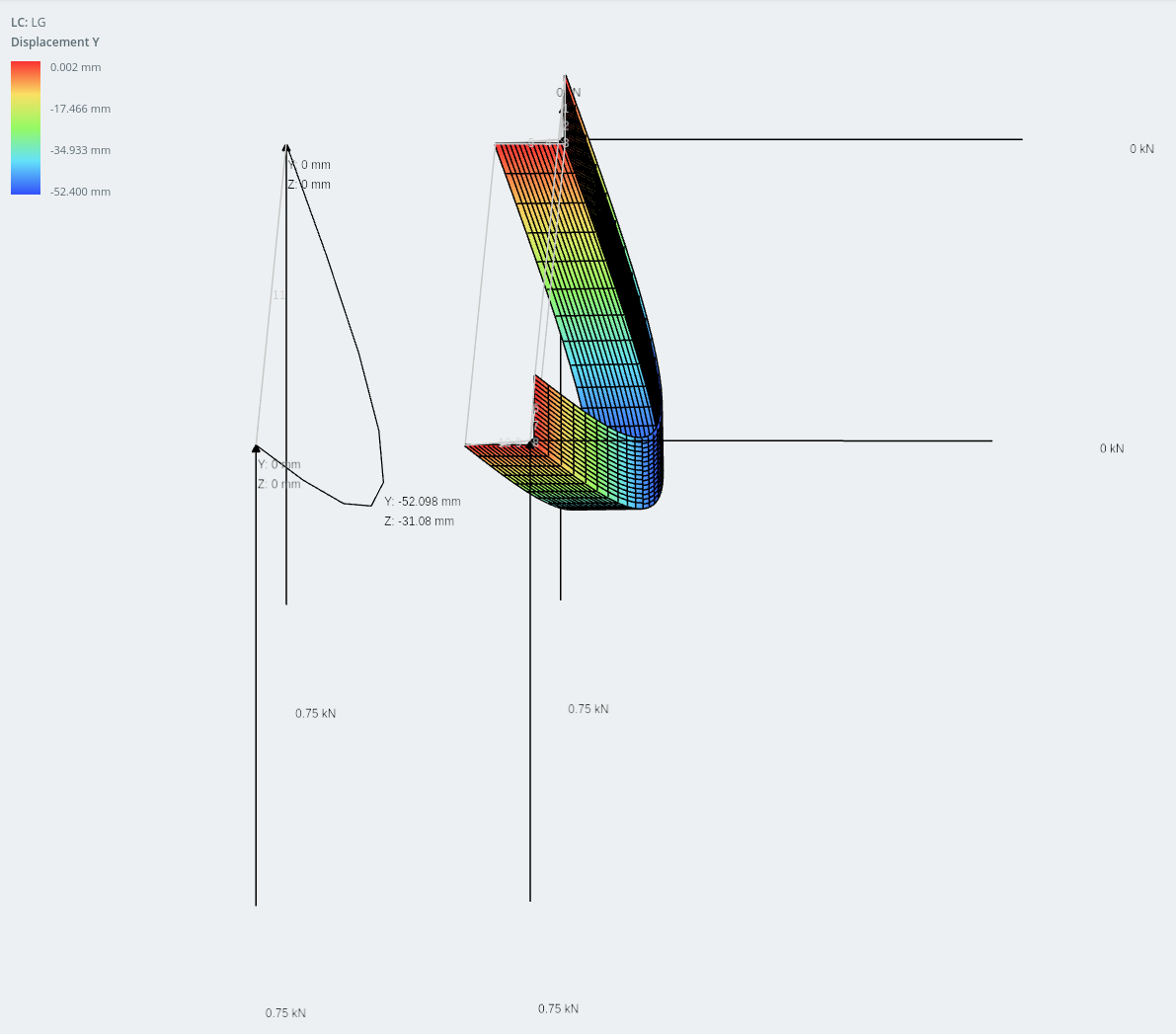
Verplaatsing in verticale richting

Het verschil in resultaten tussen de twee modellen is extreem dichtbij: binnen 1% van elkaar.

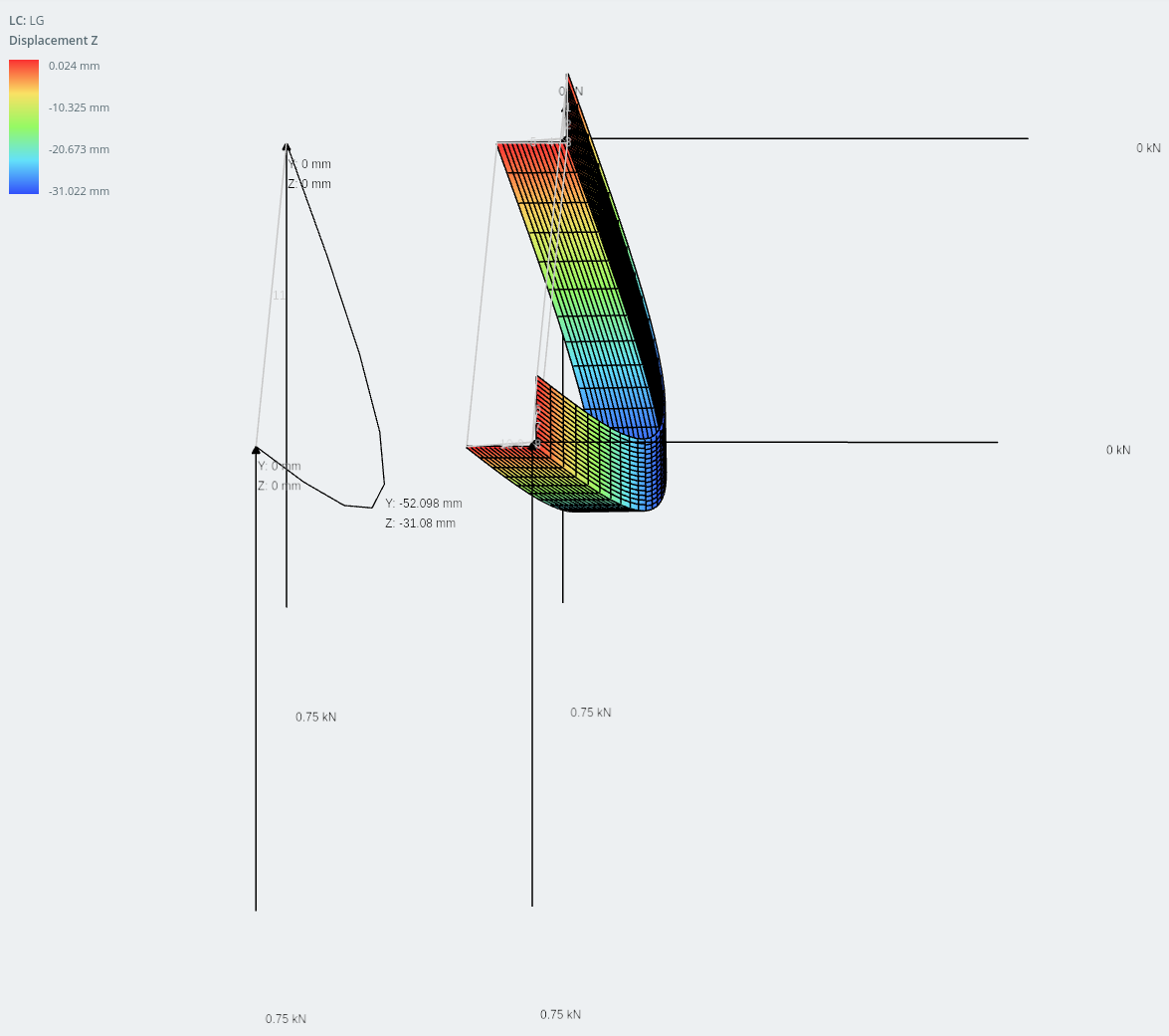
Verplaatsing in horizontale richting.

En ze worden bevestigd door de handberekeningen hieronder.

Waarom u deze secties zou willen gebruiken?

Ingenieurs ontwerpen graag constructies die licht en efficiënt zijn, soms zijn er echter beperkingen aan de vorm van structurele componenten, meestal te wijten aan ontwerpbeslissingen van anderen. Deze vormbeperking kan vele redenen hebben, het kan zijn omdat een architect structurele elementen om esthetische redenen wil verbergen, of om te voldoen aan lokale ruimtelijke ordeningswetten. Het kan zijn dat er beperkingen zijn vanwege de lokale fabricagecapaciteit of gewoon de beschikbaarheid en kosten van grondstoffen. Fabricagekosten en coating kunnen ook een belangrijke rol spelen. Soms, we zitten vast met wat we hebben.

Wanneer er een keuze is, de sectie kan worden gekozen omdat het bepaalde voordelen heeft. Neem bijvoorbeeld Z-secties, die vaak worden gezien ter ondersteuning van hellende geprofileerde staalplaten;. Typisch voor kleine schuine dakhoeken, kanalen zijn efficiënter omdat zwaartekrachtbelastingen slechts kleine momenten rond de zwakke as veroorzaken. Deze momenten nemen toe naarmate de helling van het dak toeneemt en bij een bepaalde helling, Z-secties worden efficiënter.

Om te demonstreren heb ik de lip-Z-sectie gemodelleerd als een stalen balk van 1,5 m. Hopelijk kun je na het zien van de verplaatste vorm zien waarom het een voordeel zou hebben op kanalen.

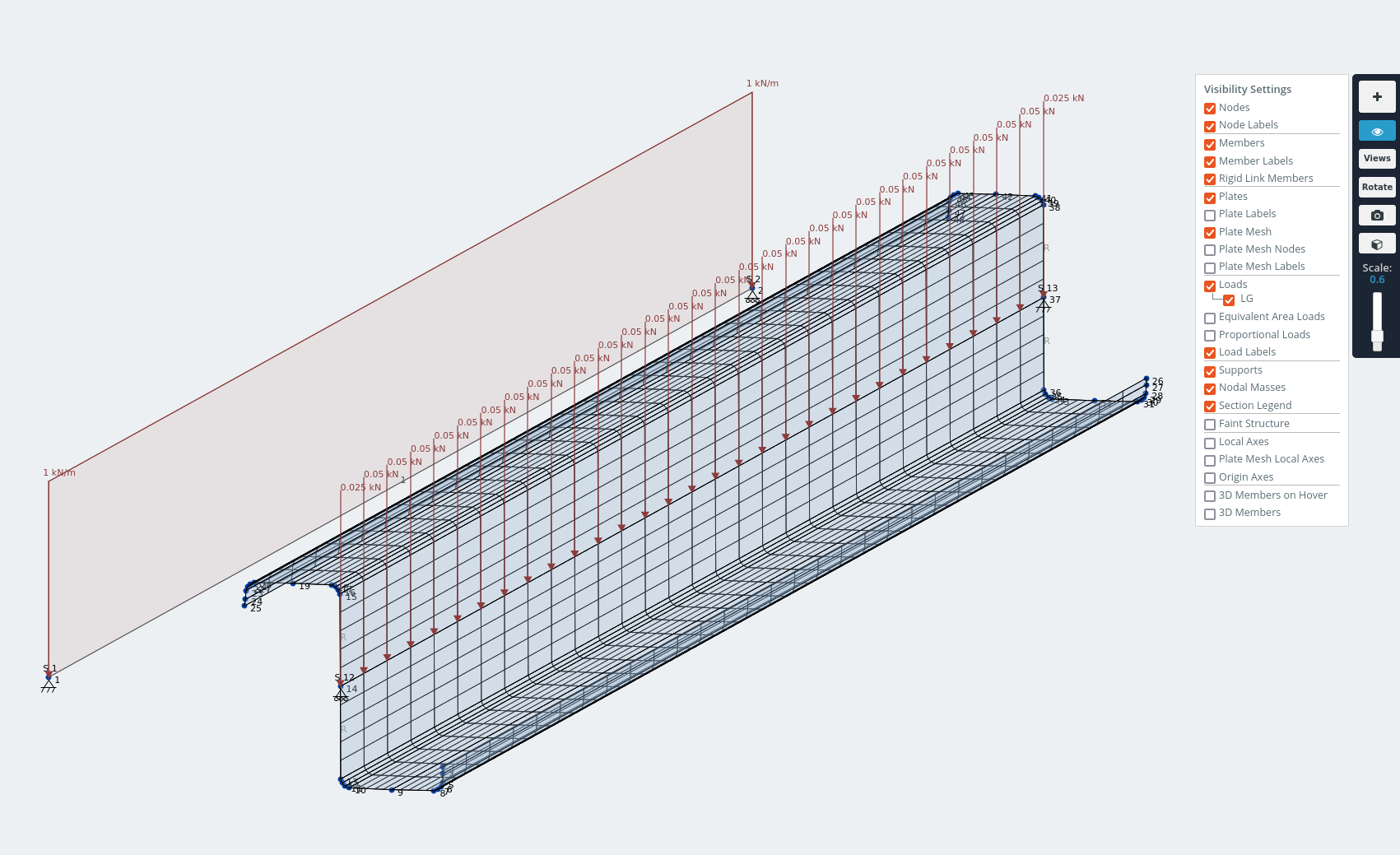
Model van lip-Z-sectie met 1 kN/m verdeelde belasting uitgeoefend door afschuifcentrum.

De verplaatsing in de z-as gaat de afschuifwerking in het vlak van de dakbedekking onder zwaartekracht tegen.

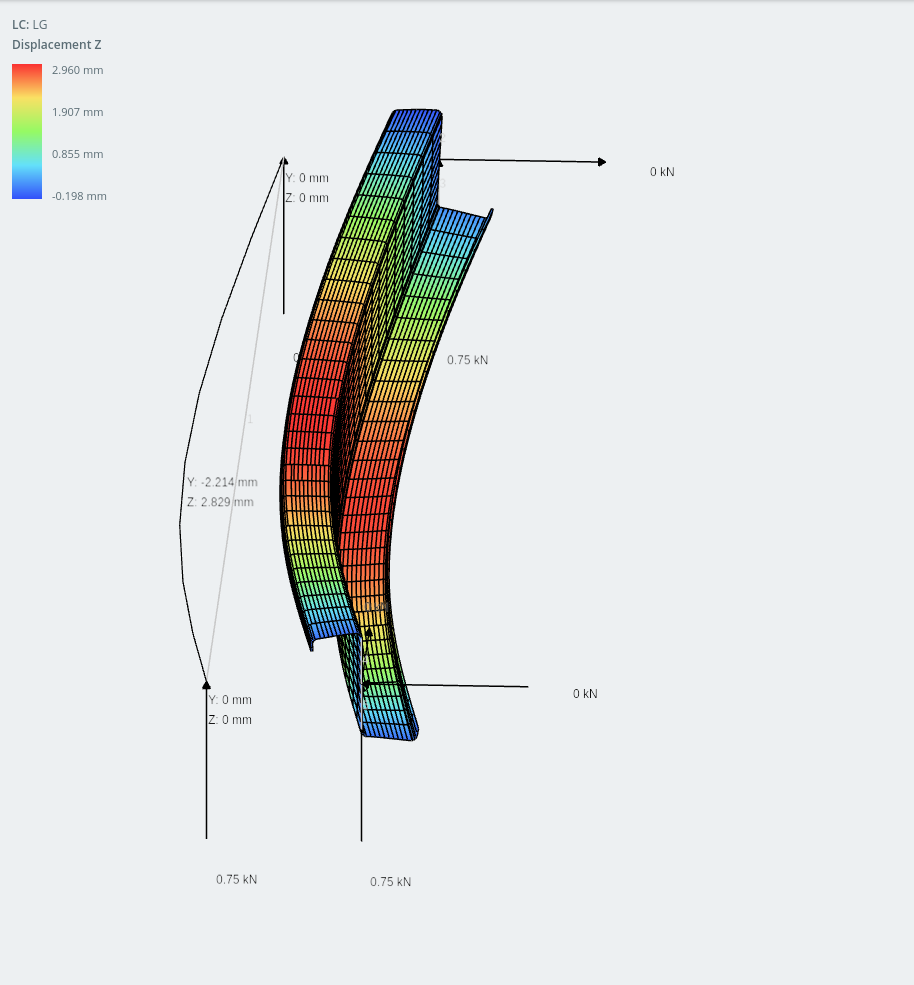
lipped-Z-sectie framemodel en schaalmodel (horizontale verplaatsing weergegeven op platen)

Verbazingwekkend, de verplaatsing in de y-as (verticaal) is eigenlijk minder dan in de horizontale. Ik moet toegeven dat ik dit soort gedrag niet had verwacht, maar met moderne koudvormtechnologie zijn er zoveel interessante manieren om secties te optimaliseren om ze lichter te maken, efficiënter, goedkoper te fabriceren, gemakkelijker te monteren en gemakkelijk te hanteren tijdens de bouw!

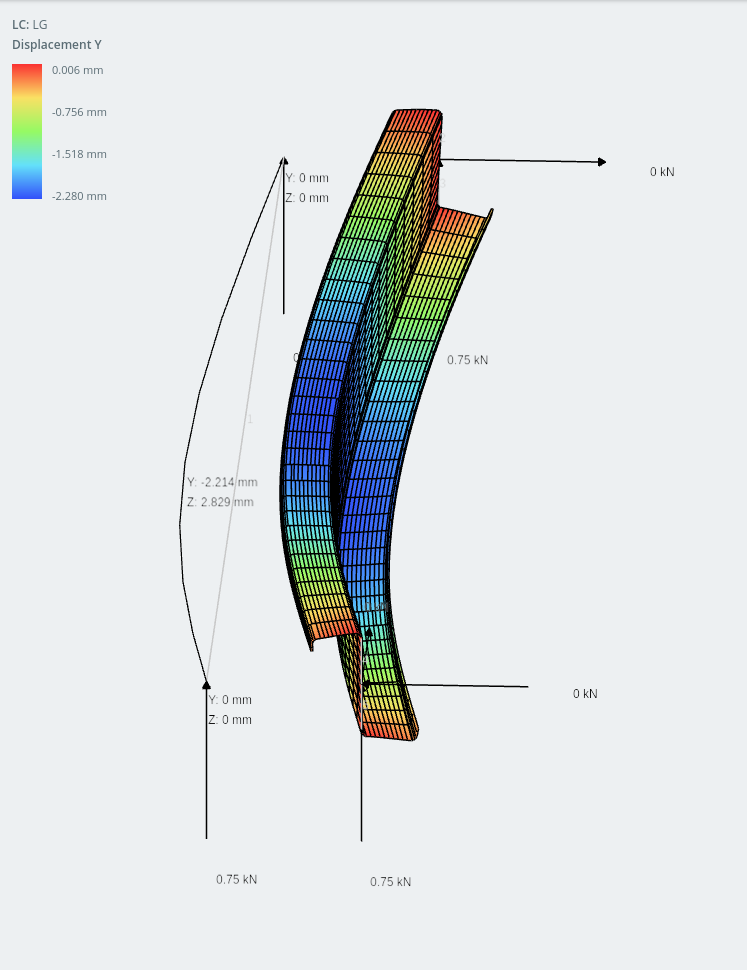
lip-Z-sectie (verticale verplaatsing getoond)

Asymmetrische secties kunnen worden ontworpen om in sommige toepassingen voordelen te hebben. Misschien overweeg je ze in je volgende ontwerp?

Ik hoop dat je dit bericht interessant vond, als je vragen of feedback hebt over asymmetrische secties, of wil je meer van dit soort inhoud zien, laat dan hieronder een reactie achter.