非対称セクション

非対称セクションは、垂直y軸または水平z軸で対称ではありません。, ある場合には, 任意の軸. 非対称セクションの例は、角度とZセクションです。.

An equal angle section
A lipped Z-section

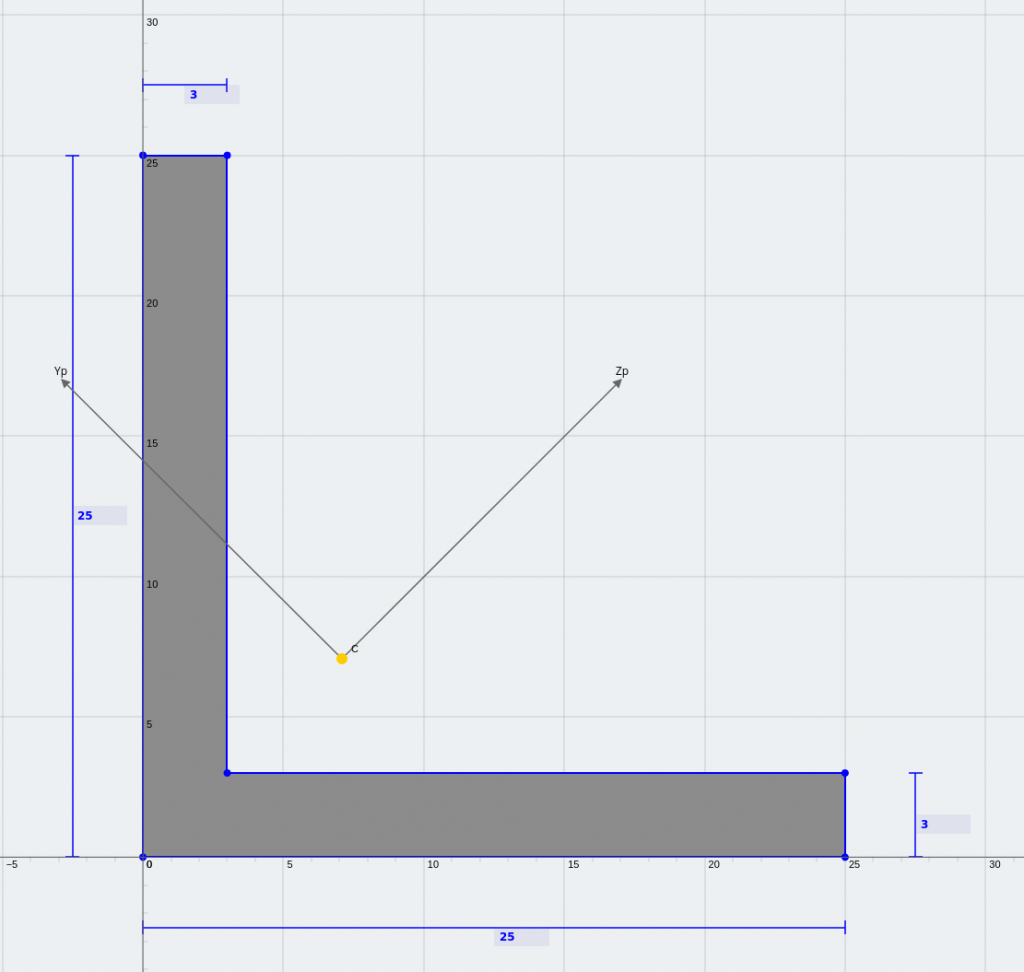
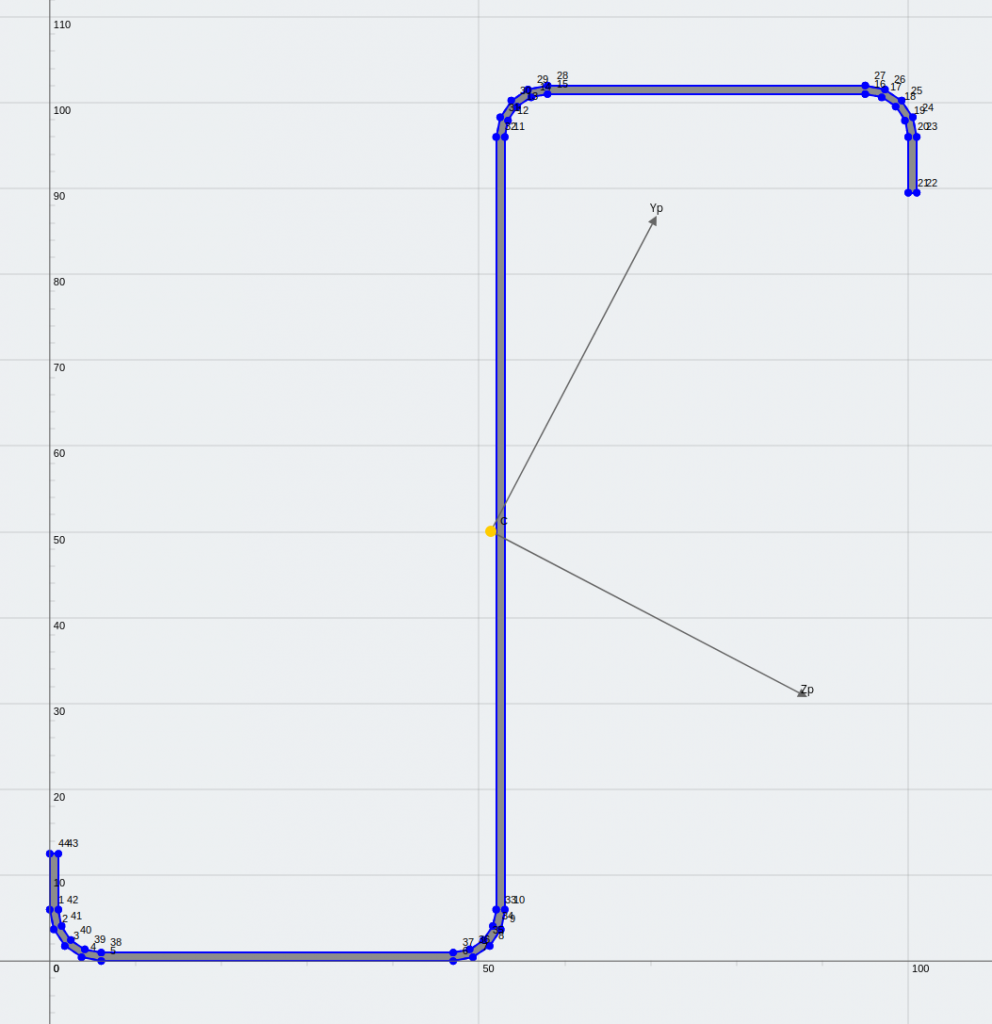
等しい角度とリップ付き Z 断面 (主軸に関して対称なミラー)

非対称断面の梁は、曲げにおいて左右対称の梁とは異なる動作をします. ビームの垂直軸の剛性が同等であっても、RHSのようには動作せず、IShapeのように動作します。.

この例では、単純な荷重ケースでそれらの動作を示します: 垂直方向に均一に分散された荷重.

分析

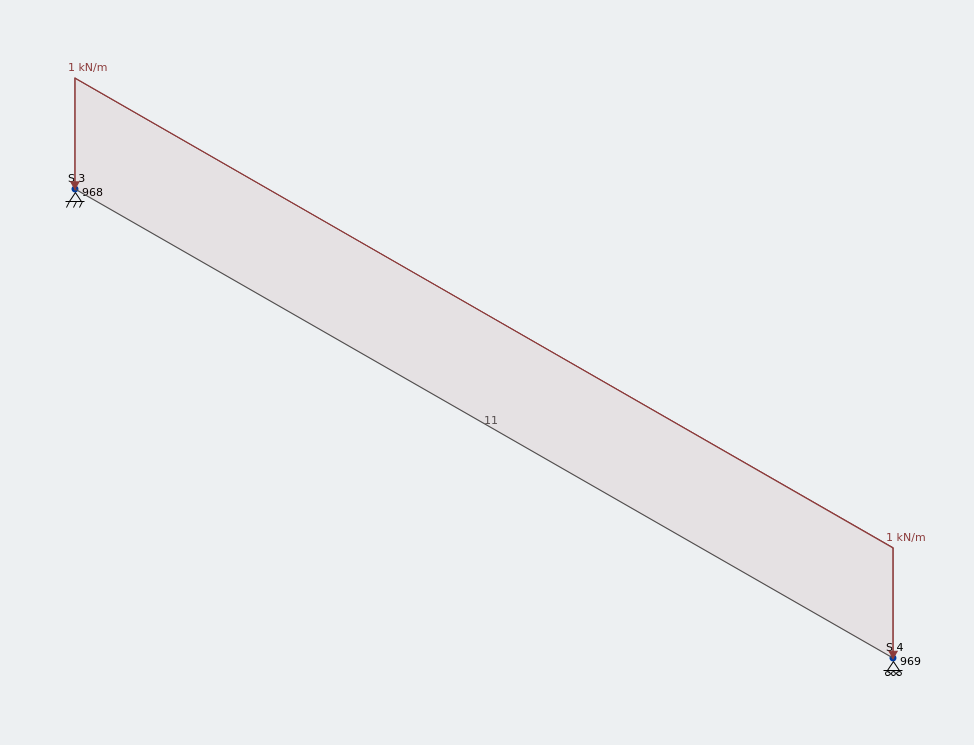
非対称セクションとは

のフレームモデル 1.5 垂直UDLの下でm等しい角度

この全長に沿って1kN / mの均一に分散された荷重を適用しました 1.5 m等しい角度.

このビームの中間スパンでのたわみを確認したい場合は、非常に簡単にできます。. 必要なのは断面二次モーメントだけです, 単純に支持された梁の標準的な最大たわみ式. SkyCiv Section Builderを使用した簡単な計算で、セクションのプロパティを簡単に取得できます.

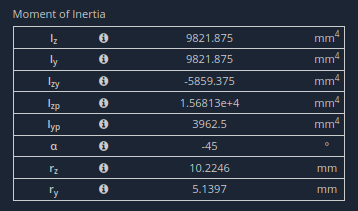
非対称断面計算

SkyCiv SectionBuilderの表形式のセクションプロパティ

Izは 9821.9 mmの4乗. セクションはE =の構造用鋼です 200 GPa.

非対称断面計算

SkyCiv Structural3DのFEAでこれを計算するとどうなるか見てみましょう.

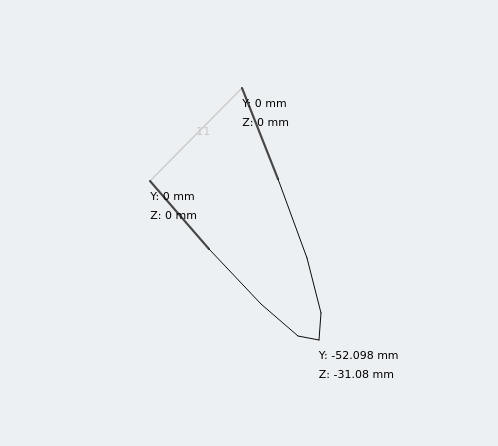
非対称セクション - 変位

荷重下での等角度の変位

等角度セクションには2つのたわみ成分があります! 前の計算を使用して左右対称の断面を使用して単純に支持されたビームのたわみを分析することは、迅速なチェックのための完全に許容できるアプローチです。. ただし、非対称セクションの場合は、別の情報が必要です.

角度α

上記のセクションのプロパティに注意してください, αの値がゼロ以外.

これは、主軸が幾何学的軸の1つと平行ではないことを意味します.

計算された剛性値に対する軸の回転の影響を示すため, 座標系を回転させたときの水平軸と垂直軸の剛性の下にプロットしました.

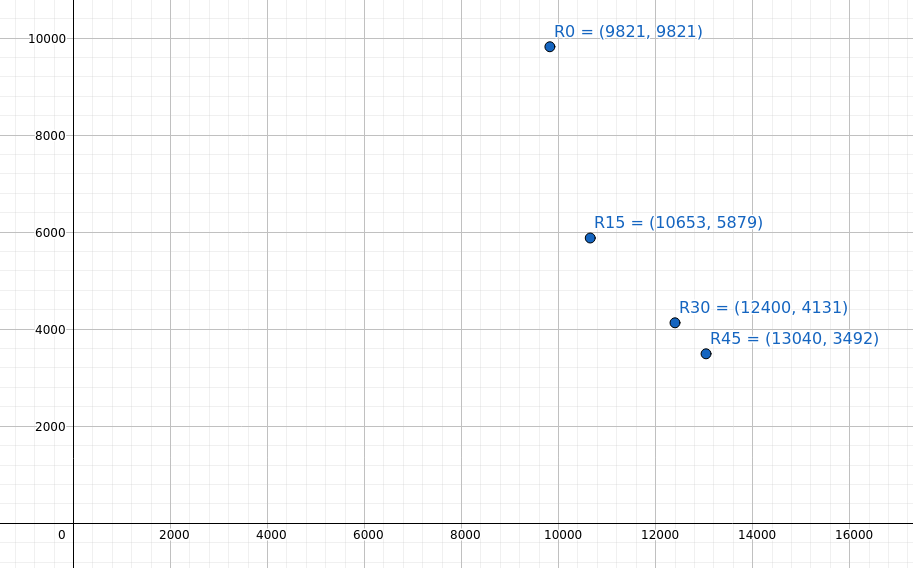
非対称セクション - 座標系を回転させた後の25x25x3EAの剛性

座標系を回転させた後の25x25x3EAの剛性

座標系が回転するときに形成される非線形曲線に注意してください 15, 30 そして 45 度. この曲線はセクションに固有のものになります.

では、なぜこれが起こっているのですか？?

講師は、荷重が構造の最も硬い部分に従うと一度私に言いました. この場合, 荷重は最も硬い軸によって運ばれています (主主軸).

正しいアプローチ

たわみ結果を計算する正しい方法は、最初にすべての荷重を主軸に変換することです。, 次に、主軸に沿った断面二次モーメントに基づいてたわみを計算します. これが本当に正しいアプローチであることを証明するために、私は手計算を使用して答えを検証しました, これをもう少し面白くするために, フレーム要素を使用したビームのモデルと, シェルから構築されたモデル. そうすれば、以前に見た変位が実際に正しいことは間違いありません。.

これが私が作成したモデルです.

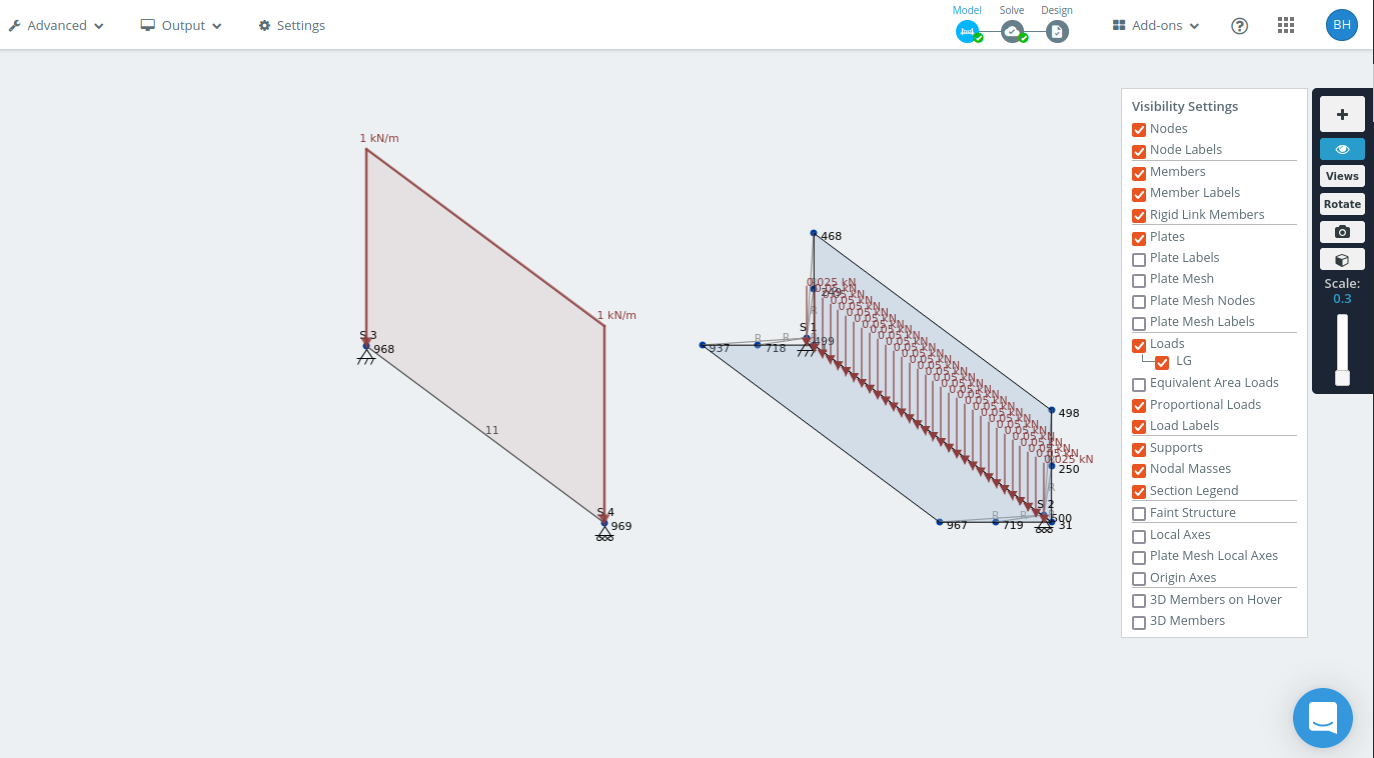
のフレームモデルとシェルモデル 1.5 m角度 - 非対称セクション

のフレームモデルとシェルモデル 1.5 m角度

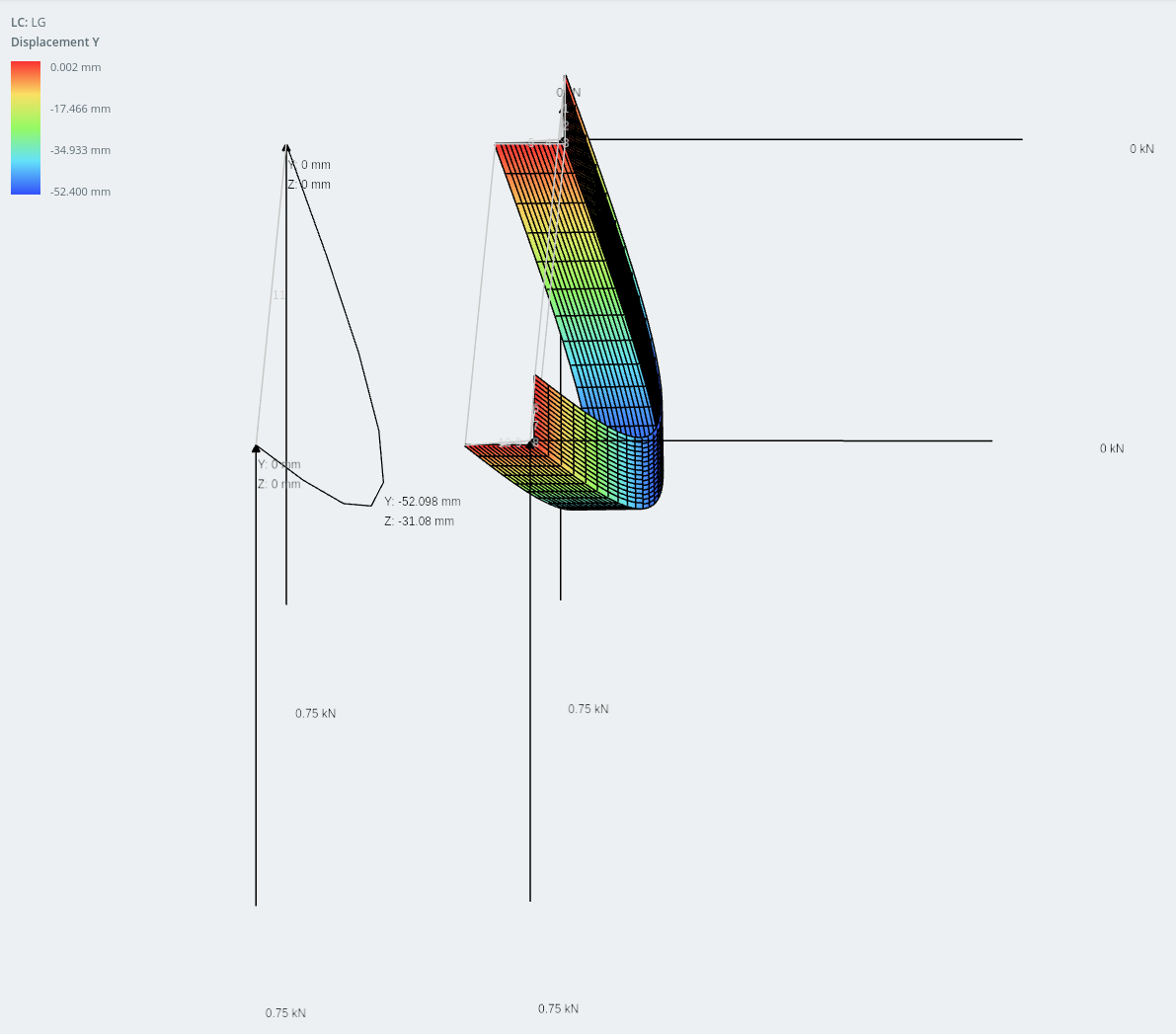
垂直方向の変位 - 非対称セクション

垂直方向の変位

2つのモデル間の結果の違いは非常に近いです: 以内に 1% お互いの.

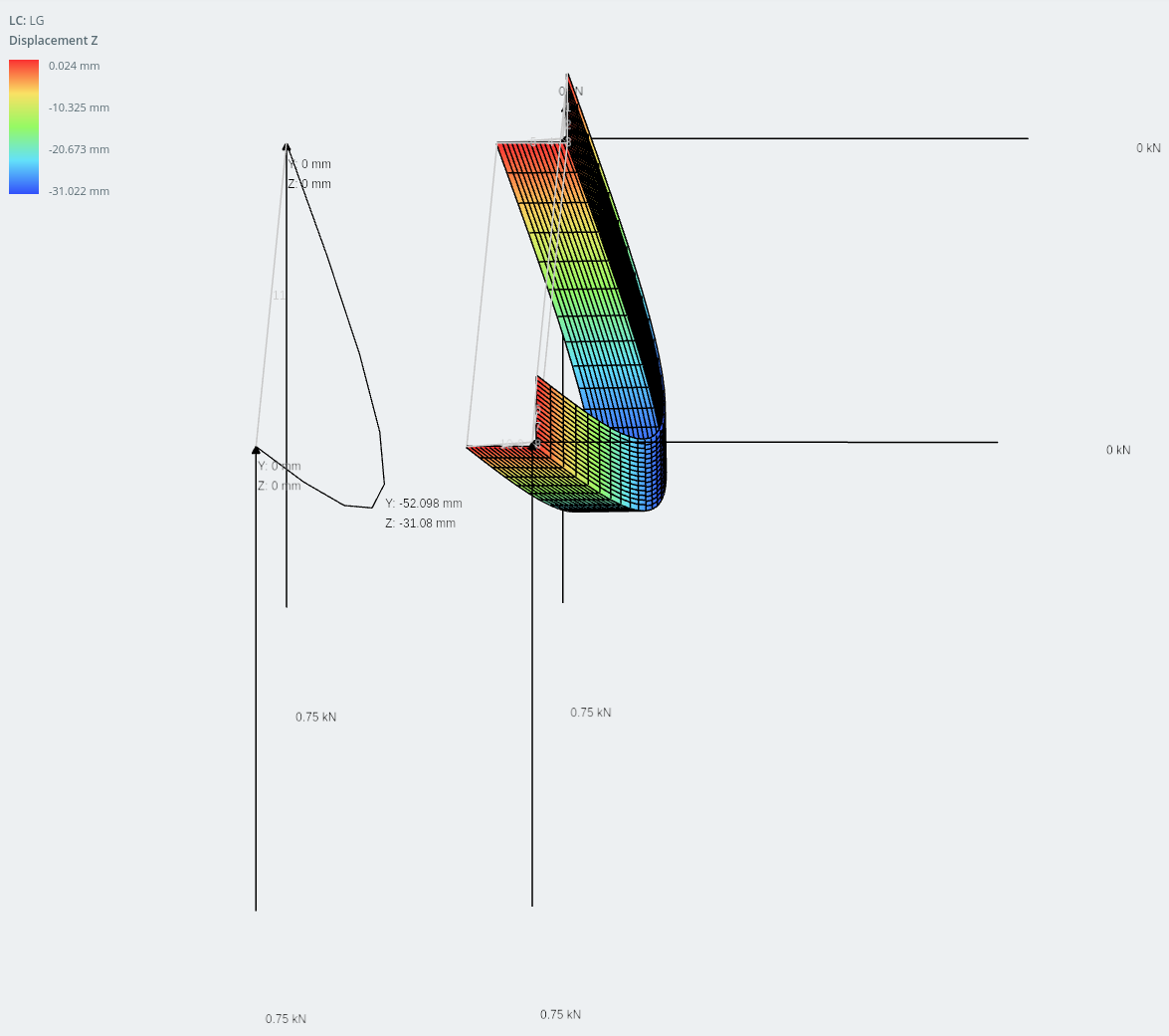
水平方向の変位 - 非対称セクション

水平方向の変位.

そして、それらは以下の手計算によって確認されます.

非対称セクション - 手計算

これらのセクションを使用する理由?

エンジニアは、軽量で効率的な構造を設計するのが好きです, ただし、構造コンポーネントの形式に制限がある場合があります, 通常、他の人による設計上の決定が原因です. フォームに対するこの制約は、多くの理由で発生する可能性があります, 建築家が美的理由で構造要素を隠したいからかもしれません, または地域の計画法を遵守するため. 現地の製造能力、または単に原材料の入手可能性とコストによる制限がある可能性があります. 製造コストとコーティングも重要な役割を果たす可能性があります. 時々, 私たちは私たちが持っているもので立ち往生しています.

選択肢があるとき, 特定の利点があるため、セクションを選択できます. Zセクションを例にとってみましょう, 傾斜したプロファイルの鋼板をサポートするのが一般的に見られます. 通常、傾斜した屋根の角度が小さい場合, 重力荷重は弱い軸の周りにわずかなモーメントしか引き起こさないため、チャネルはより効率的です. これらのモーメントは、屋根の傾斜が増加するにつれて、特定の傾斜で増加します, Zセクションがより効率的になります.

デモンストレーションのために、リップドZセクションを1.5mの鋼製ビームとしてモデル化しました. 変形した形状を見て、なぜそれがチャネル上で有利であるかがわかると思います。.

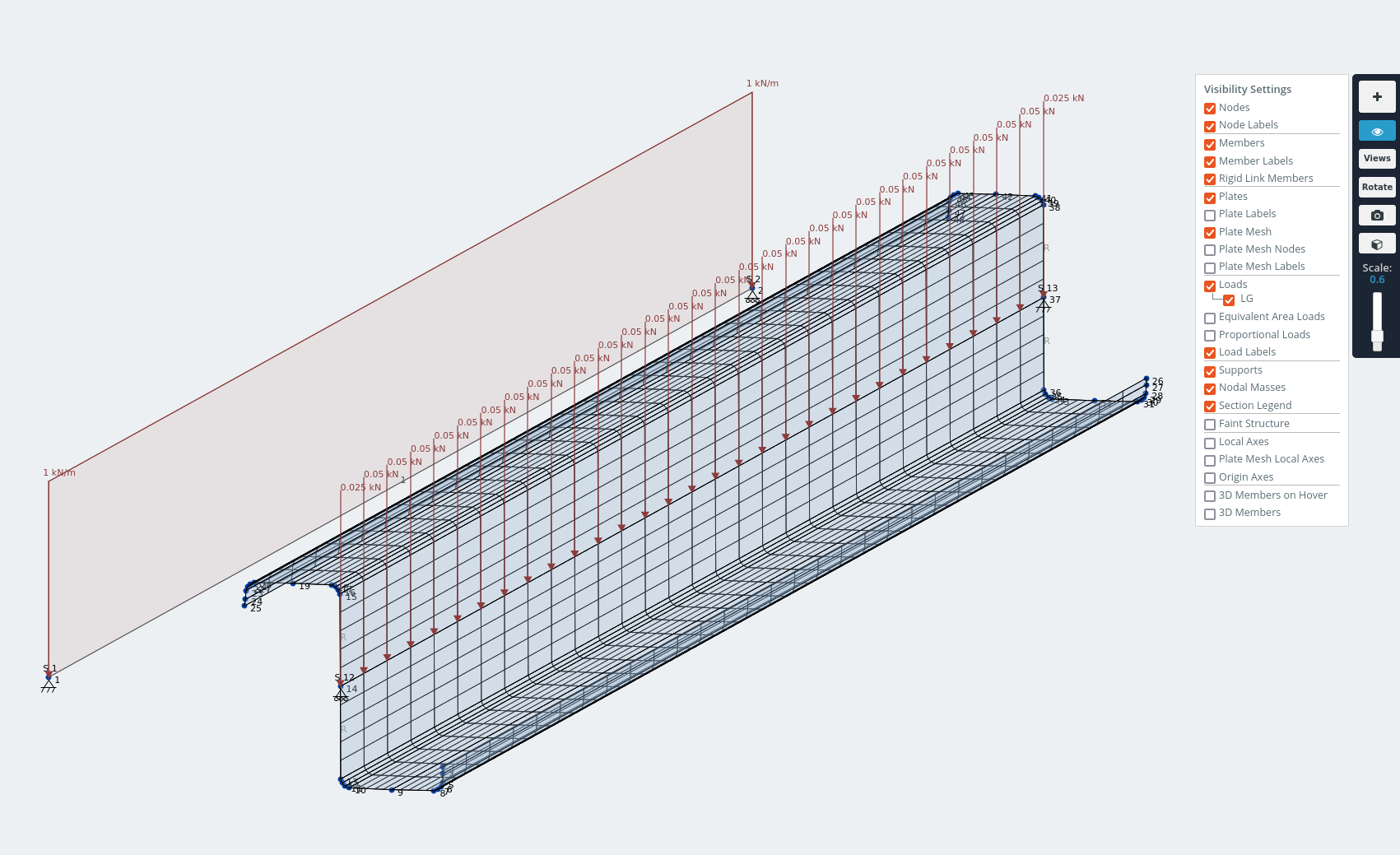
せん断中心を介して1kN / mの分布荷重が加えられたリップドZセクションのモデル - 非対称セクション

せん断中心を介して1kN / mの分布荷重が加えられたリップドZセクションのモデル.

z軸の変位は、重力荷重下での屋根シートの面内せん断作用に対抗します。.

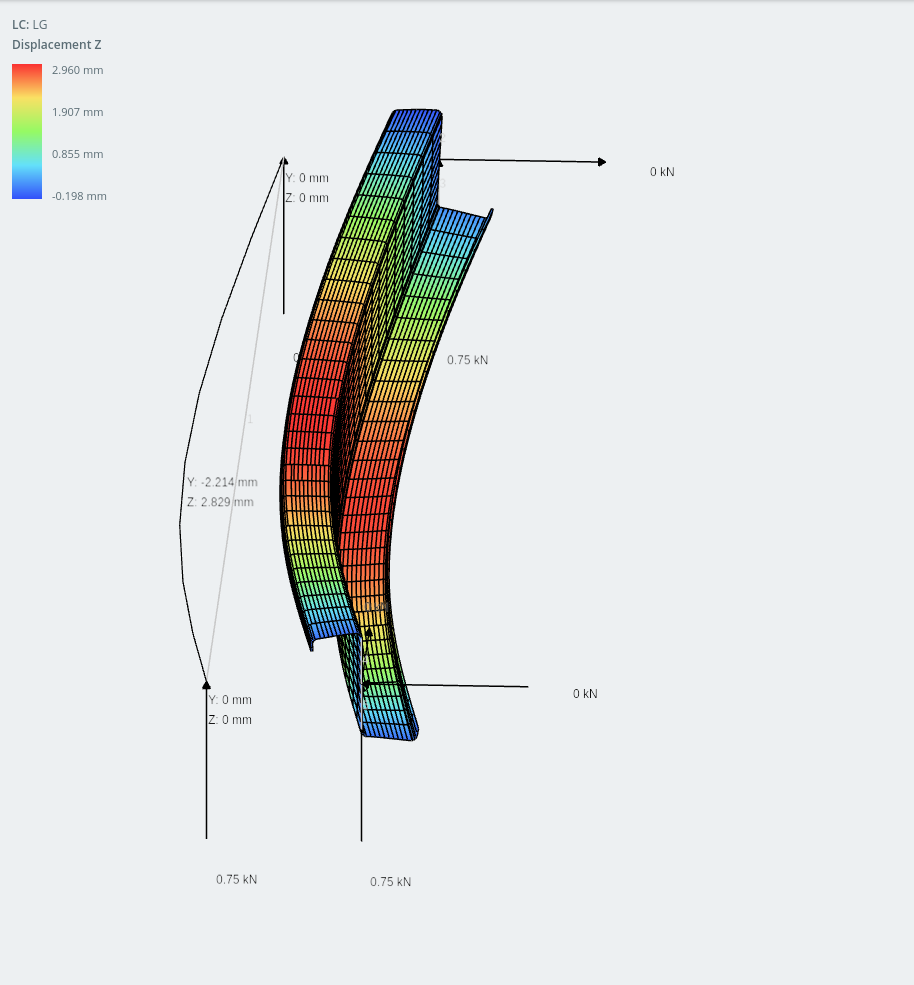
リップドZセクションフレームモデルとシェルモデル (プレートに表示される水平方向の変位) - 非対称セクション

リップドZセクションフレームモデルとシェルモデル (プレートに表示される水平方向の変位)

驚くほど, y軸の変位 (垂直) 実際には水平よりも少ないです. この種の動作は予想していなかったということを認めなければなりませんが、最新の冷間成形技術では、セクションを最適化して軽量化する興味深い方法がたくさんあります。, もっと効率的, 安価に製造できる, 組み立てが簡単で、建設中の取り扱いが簡単です!

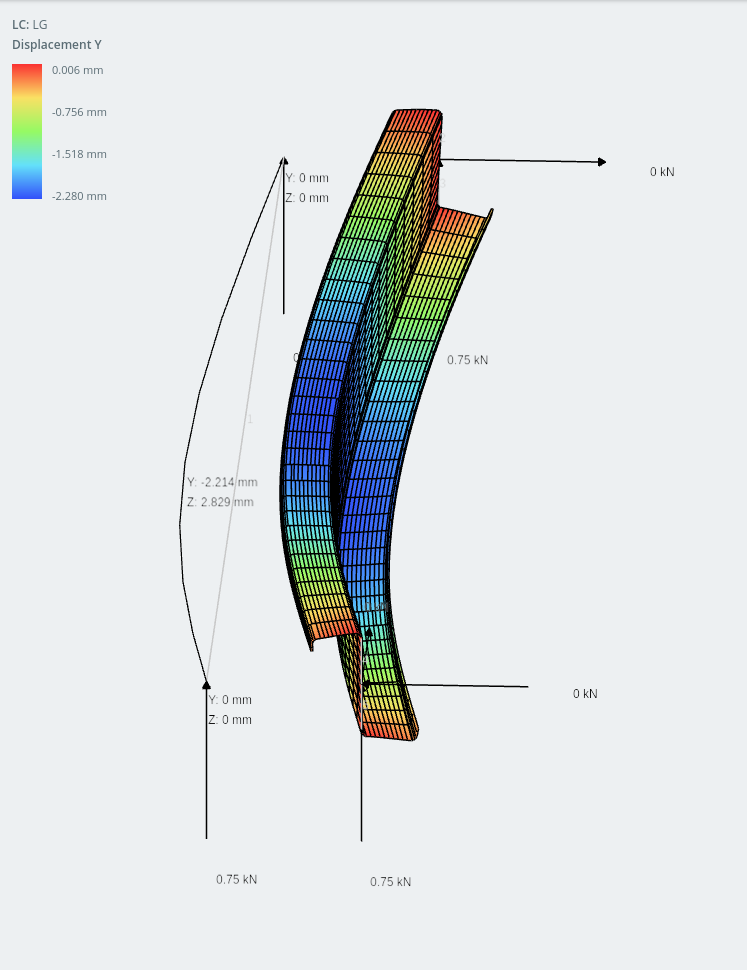
リップドZセクション (示されている垂直変位) - 非対称セクション

リップドZセクション (示されている垂直変位)

非対称セクションは、一部の用途で利点が得られるように設計できます。. 次のデザインでそれらを検討するかもしれません?

この投稿がおもしろいと思います, 非対称セクションについて質問やフィードバックがある場合, または、このようなコンテンツをもっと見たい場合は、下にコメントを残してください.