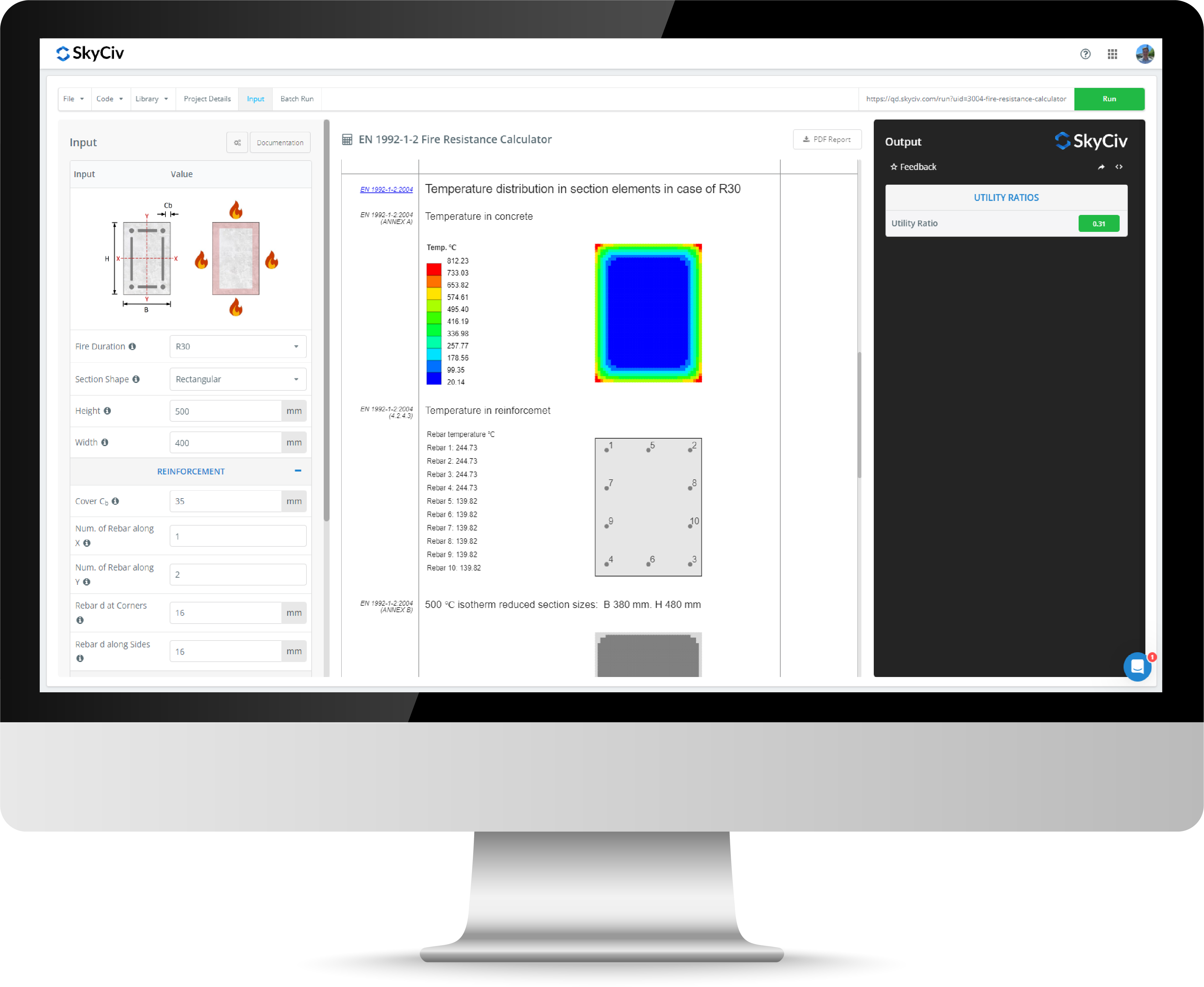
断面特性計算ツール

上記の重心計算ツールは、関連する重心方程式を使用して円の重心を見つけます。, 矩形, 中空の長方形, アイビーム, チャンネルとアングルセクション. 計算機は重心を含む簡略化された結果を返します。 (X 方向と Y 方向の両方で) いくつかの単純な断面寸法入力から. 断面図心は形状の幾何学的中心です, 面積のバランスが均等になる点を表す. セクション内の内容が一貫していると仮定する, それがそのセクションの重心になります. 重心は通常、Cx と Cy によって定義されます。, セクションの底部からの距離をそれぞれ x と y で表します. したがって、重心の位置は点として表すことができます [CX, Cy].

一部の形状については, これは非常に単純な計算です. 例えば, 長方形の重心を見つけるのは、高さと幅を半分にするのと同じくらい簡単です。:

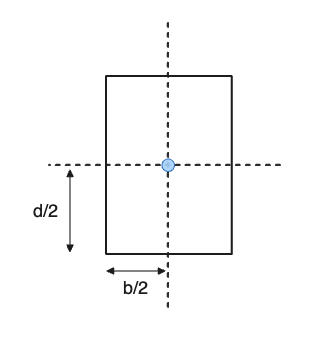
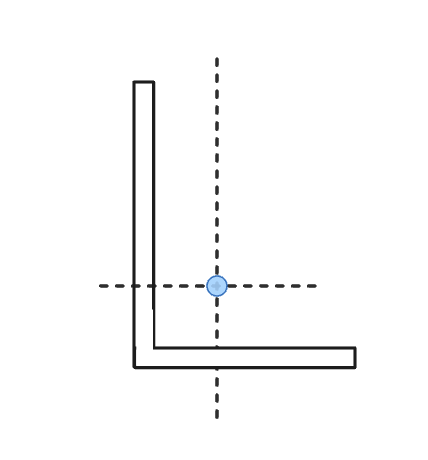
しかしながら, 両方の軸で対称ではない、より複雑なセクションの場合, 重心の計算はもう少し複雑です. 例えば, 角度断面図の重心が実際の断面図から離れた場所にある可能性があります:

断面係数は重要な幾何学的特性です, これは最終的にセクションが曲げにどれだけ耐えられるかを表します。. 次の単純な弾性断面係数式によって計算されます。:

S_xb = 私_xx / Cそして

上記の断面係数の式は、断面の最下部の繊維までの x 軸周りの弾性断面係数を表します。. 断面係数のプロパティは、多くの場合、4 つの結果に分類されます。, 個別の結果付き:

• S_xb: 断面の底部までの x 軸周りの断面係数
• S_xt: 断面の上部までの x 軸周りの断面係数
• S_yt: 断面の上部までの y 軸周りの断面係数 (またはセクションの右端の部分)
• S_yb: 断面の底部までの y 軸周りの断面係数 (またはセクションの左端の部分)

注意することも重要です, x/z 軸は互換的に使用できます. だから例えば, 私たちのセクションのモジュラス計算, を使用しております と の代わりに バツ 私たちの横軸として.

弾性断面係数 (S) 対プラスチック断面係数 (と)

弾性断面係数 (S) 弾性限界内のセクションの曲げ挙動を表します - 荷重がかかると変形しますが、荷重が取り除かれると元の形状に戻ります。. この係数は、降伏する前の最大曲げ応力を計算するために重要です。.

一方, プラスチックの断面係数 (と) セクションの曲げ動作をキャプチャします 超えて その弾性限界, 塑性変形するところ. Z は、降伏後の応力を再分配するメンバーの能力を表します。, 曲げに対する耐性を強化する.

Sながら (弾性のある) 弾性範囲内で動作する構造を設計するための基本です, と (プラスチック) 塑性挙動が予想される、または望ましいシナリオでの応用が見出されます。, コンパクトなセクションを扱う場合の鋼材設計など, プラスチック断面係数を使用して設計をさらに推し進めることができます. 非コンパクトセクションの場合, 塑性モーメント容量に達する前にセクションが局部的に座屈します。 - 従って 弾性断面係数 この場合に使用されます. これについて詳しくは、SkyCiv のガイドをご覧ください。 AS4100 スチール設計, ただし、これはオーストラリアの規格に具体的に言及しています。, についての有益な一般的なコメントが含まれています 鋼設計における断面分類.

異なる地域では、塑性係数と弾性係数の異なる命名法が採用されていることにも注意することが重要です。:

オーストラリア
Z = 弾性, S = プラスチック

アメリカ + 世界のその他の地域
S = 弾性, Z = プラスチック

• アルミニウム設計ソフトウェア
• AISC 360 Iビーム耐荷重計算機
• CSA O86-14 木材設計ソフトウェア
• ユーロコード 5 木と木材の構造設計のためのソフトウェア
• なので 4100:2020 鋼の設計ソフトウェア