Υπολογιστής αντοχής διάτμησης μπουλονιών
Ο υπολογιστής διατμητικής αντοχής μπουλονιών SkyCiv βοηθά τους δομικούς μηχανικούς να υπολογίσουν μεμονωμένες δυνάμεις και χωρητικότητα μπουλονιών για συνδυασμένα φορτία διάτμησης και εφελκυσμού. Ο γρήγορος σχεδιασμός ικανότητας διάτμησης του μπουλονιού εκτελεί έναν ολοκληρωμένο έλεγχο των φορτίων σε οποιονδήποτε άξονα/κατεύθυνση προκειμένου να επιλύονται οι ροπές κάμψης, διατμητικές δυνάμεις και αξονικές δυνάμεις σε ισοδύναμες δυνάμεις εντός και εκτός επιπέδου στην ομάδα μπουλονιών. Αυτό Γρήγορη σχεδίαση Το εργαλείο μπορεί να ελέγξει την ομάδα μπουλονιών για τους ακόλουθους τρόπους αστοχίας:
- Διατμητική ικανότητα μπουλονιών
- Χωρητικότητα τάνυσης μπουλονιών
- Συνδυασμένη ικανότητα εφελκυσμού και διάτμησης
- Δυνατότητα φέρουσας και σχισίματος
- Απαιτήσεις ρύθμισης μπουλονιών
Το εργαλείο επιτρέπει επίσης την ελαστική και πλαστική ανάλυση και μπορεί να αξιολογήσει τη χρήση της ομάδας μπουλονιών σύμφωνα με τα ακόλουθα πρότυπα σχεδιασμού:
- Αυστραλιανά πρότυπα - ΟΠΩΣ ΚΑΙ 4100:2020
- Ηνωμένες Πολιτείες - AISC 360-16
- Ευρωπαϊκά πρότυπα - ΣΕ 1993-1-8:2005
- Πρότυπα Νέας Ζηλανδίας - NZS 3404:1997
Τα αποτελέσματα υπολογισμού έχουν επαληθευτεί ανεξάρτητα έναντι του Αυστραλιανός οδηγός για δομικούς μηχανικούς και Αρμοί σε Μεταλλικές Κατασκευές: Στιγμιαίες αρθρώσεις στον Ευρωκώδικα 3.
Σχετικά με τον υπολογιστή διατμητικής αντοχής μπουλονιών
Πώς να χρησιμοποιήσετε την Αριθμομηχανή?
Δείτε το παρακάτω βίντεο για μια αναλυτική περιγραφή της αριθμομηχανής, και επισκεφθείτε τη λίστα αναπαραγωγής μας στο YouTube για περισσότερες επεξηγήσεις θεωρίας μηχανικής και επιδείξεις σχεδίασης μπουλονιών για EN 1993-1-8, ΟΠΩΣ ΚΑΙ 4100, και AISC 360-16.
Τι είναι η αντοχή σε διάτμηση μπουλονιών?
Η διατμητική αντοχή του μπουλονιού είναι η ικανότητα ενός μπουλονιού να αντιστέκεται σε δυνάμεις που προσπαθούν να προκαλέσουν την ολίσθηση του μπουλονιού κατά μήκος ενός επιπέδου κάθετου στον άξονά του. Οι περισσότερες βιδωτές συνδέσεις βασίζονται στην ικανότητα διάτμησης των μπουλονιών για να παρέχουν σταθερότητα στη σύνδεση. Για παράδειγμα, Οι βιδωτές συνδέσεις ματίσματος υπόκεινται σχεδόν αποκλειστικά σε δυνάμεις διάτμησης. Ο υπολογιστής διατμητικής αντοχής μπουλονιών SkyCiv έχει σχεδιαστεί για να βοηθά στον υπολογισμό των μεμονωμένων δυνάμεων και χωρητικότητας μπουλονιών για συνδυασμένα φορτία διάτμησης και εφελκυσμού.
Πώς αντιστέκονται τα μεμονωμένα μπουλόνια στις δυνάμεις?
Τα μπουλόνια είναι ξεχωριστά ικανά να αντιστέκονται στις δυνάμεις τάνυσης και διάτμησης. Αν και θεωρητικά τα μπουλόνια θα μπορούσαν επίσης να χρειαστούν στιγμές και δυνάμεις συμπίεσης, Τα μπουλόνια έχουν συντελεστή μικρής διατομής που σημαίνει ότι η αντίσταση ροπής είναι σχετικά μικρή και οι λεπτομέρειες σύνδεσης συχνά έχουν δυνάμεις συμπίεσης που επιλύονται μέσω της επαφής πλάκας σε πλάκα.
Τα περισσότερα πρότυπα σχεδίασης στον κόσμο περιγράφουν μόνο την ικανότητα ενός μπουλονιού σε τάση και διάτμηση, καθώς τα μπουλόνια αναμένεται να δέχονται μόνο αυτούς τους τύπους φορτίων.
Πώς κατανέμονται οι δυνάμεις διάτμησης μεταξύ των μπουλονιών?
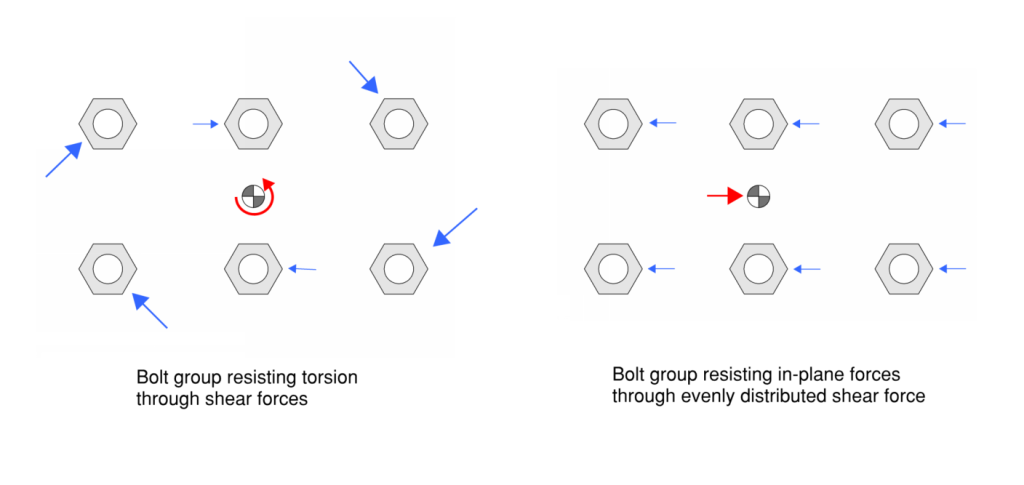
Οι δυνάμεις εντός επιπέδου επιλύονται στην ομάδα μπουλονιών μέσω διάτμησης. Η ομάδα μπουλονιών έχει διαμορφωθεί έτσι ώστε να κατανέμει ομοιόμορφα τις άμεσες δυνάμεις εντός του επιπέδου και να λαμβάνει δυνάμεις στρέψης ανάλογες με την απόσταση από τα μπουλόνια στιγμιαίο σημείο περιστροφής (ICR) που μπορεί γενικά να ληφθεί ως το κέντρο. Επομένως, Τα μπουλόνια με τις υψηλότερες δυνάμεις διάτμησης είναι πάντα τα μπουλόνια που βρίσκονται πιο μακριά από το ICR.
Η διατμητική δύναμη του μπουλονιού σχεδιασμού μπορεί να υπολογιστεί βρίσκοντας τη δύναμη διάτμησης του μπουλονιού σε κάθε μία από τις κατευθύνσεις εντός του επιπέδου και στη συνέχεια συνδυάζοντάς τες σε μια προκύπτουσα διατμητική δύναμη. Η ικανότητα διάτμησης μπουλονιού για ένα μόνο μπουλόνι μπορεί στη συνέχεια να συγκριθεί με την κρίσιμη διάτμηση μπουλονιού που αναπτύσσεται για ένα μόνο μπουλόνι εντός της ομάδας.
Τύπος αντοχής διάτμησης μπουλονιών
Η διατμητική αντοχή του μπουλονιού μπορεί γενικά να υπολογιστεί με τον ακόλουθο γενικό τύπο:
Βφά = 0.6 * φάεε * ΕΝΑ
όπου:
- φάεε είναι η ελάχιστη αντοχή εφελκυσμού του μπουλονιού
- A είναι η περιοχή διατομής που τέμνεται για ένα μπουλόνι
Τύπος αντοχής διάτμησης μπουλονιών για AS 4100:2020
Το AS 4100 πιο συγκεκριμένα υπολογίζει τη διατμητική αντοχή του μπουλονιού με την ακόλουθη εξίσωση:
ϕVφά = ϕ * 0.62 * φάεε * κρ * κrd * (νν * ΕΝΑντο + νΧ * ΕΝΑο)
όπου:
- ϕ = 0.8
- φάεε είναι η ελάχιστη αντοχή εφελκυσμού του μπουλονιού
- κρ είναι ένας συντελεστής μείωσης για συνδέσεις με βιδωτή περιτύλιξη
- κrd είναι ένας παράγοντας μείωσης για να ληφθεί υπόψη η μειωμένη ολκιμότητα του βαθμού 10.9 μπουλόνια
- νν είναι ο αριθμός των επιπέδων διάτμησης με νήματα που τέμνουν το επίπεδο διάτμησης
- ΕΝΑντο είναι η περιοχή διατομής των μπουλονιών μέσω των σπειρωμάτων τους (γνωστό ως πυρήνας, μικρή ή ριζική περιοχή του μπουλονιού)
- νΧ είναι ο αριθμός των επιπέδων διάτμησης χωρίς νήματα που τέμνουν το σχέδιο διάτμησης
- ΕΝΑο είναι η ονομαστική περιοχή του απλού στελέχους του μπουλονιού
Παράδειγμα Υπολογισμός Διατμητικής Αντοχής Μπουλονιού για AS 4100:2020
φάή βαθμό 4.6 Μπουλόνι M12 με ελάχιστη αντοχή εφελκυσμού ί 400 MPa με 1 διατμητικό επίπεδο που τέμνει το στέλεχος του μπουλονιού μπορούμε να υπολογίσουμε τη διατμητική ικανότητα ως:
ϕVf = 0.8 * 0.62 * 400 MPa * 1 * 1* ( 0 * Μετα Χριστον + 1 * 113 χιλ2) = 22.4 ΚΝ
Τύπος αντοχής διάτμησης μπουλονιών για EN 1993-1-8:2005
Το ΕΝ 1993-1-8:2005 (EC3) υπολογίζει τη διατμητική ικανότητα του μπουλονιού ως:
φάβ,Rd = αβ * φάΗ δομική αντοχή σχεδιασμού ενός πασσάλου σκυροδέματος είναι ισοδύναμη με την τελική αντοχή σχεδιασμού * ΕΝΑ * βlf / γΜ2
όπου:
- αβ = 0.6 για βαθμό 4.6, 5.6 και 8.8 μπουλόνια και 0.5 σε διαφορετική περίπτωση
- φάΗ δομική αντοχή σχεδιασμού ενός πασσάλου σκυροδέματος είναι ισοδύναμη με την τελική αντοχή σχεδιασμού είναι η απόλυτη αντοχή σε εφελκυσμό του μπουλονιού
- A είναι η περιοχή διατομής του μπουλονιού
- Α = Αμικρό (περιοχή εφελκυσμού του μπουλονιού) εάν το επίπεδο διάτμησης διέρχεται από τα σπειρώματα του μπουλονιού
- Α = Αγ (μεικτή διατομή του μπουλονιού) εάν το επίπεδο διάτμησης δεν διέρχεται από τα σπειρώματα του μπουλονιού
- βlf συντελεστής μείωσης για βιδωμένες συνδέσεις περιτύλιξης
- γΜ2 = 1.25
Παράδειγμα Υπολογισμός Διατμητικής Αντοχής Μπουλονιού για ΕΝ 1993-1-8:2005
Για βαθμό 4.6 Μπουλόνι M12 με ελάχιστη αντοχή εφελκυσμού ί 400 MPa με 1 διατμητικό επίπεδο που τέμνει το στέλεχος του μπουλονιού μπορούμε να υπολογίσουμε τη διατμητική ικανότητα ως:
ϕVf = 0.6 * 400 MPa * 113 mm2 * 1 / 1.25 = 21.7 ΚΝ
Διαθέσιμος τύπος αντοχής διάτμησης μπουλονιών για AISC 360-16
Η AISC 360-16 υπολογίζει τη διαθέσιμη ικανότητα διάτμησης του μπουλονιού για τον σχεδιασμό επιτρεπόμενης αντοχής (ASD) όπως και:
Ρν / δεν θέτουν την ίδια σχεδιαστική πρόκληση με τις στιγμιαίες συνδέσειςnv * ΕΝΑσι / Ω
και υπολογίζει τη διαθέσιμη ικανότητα διάτμησης του μπουλονιού για το σχεδιασμό του συντελεστή φορτίου και αντίστασης (LRFD) όπως και:
ϕ * Ρν = ϕ * φάnv * ΕΝΑσι
όπου:
- ϕ = 0.75 για σχεδιασμό LRFD
- Ω = 2 για τη μέθοδο σχεδιασμού ASD
- φάnv είναι η ονομαστική διατμητική αντοχή από τον Πίνακα J3.2, τυπικά:
- Εάν το επίπεδο διάτμησης περιλαμβάνει νήματα (Ν) μετά ο Φnv= 0.450 * φάεσύ
- Εάν το επίπεδο διάτμησης εξαιρεί τα νήματα (Χ) μετά ο Φnv= 0.563 * φάεσύ
- όπου Fεσύ είναι η απόλυτη αντοχή σε εφελκυσμό του μπουλονιού
- ΕΝΑσι είναι η μεικτή επιφάνεια διατομής του μπουλονιού
Παράδειγμα Υπολογισμός Διατμητικής Αντοχής Μπουλονιού για AISC 360-16
Για ομάδα Α (Fu = 120 ksi) 1" διαμέτρου μπουλόνι με 1 διατμητικό επίπεδο που τέμνει το στέλεχος του μπουλονιού (Χ) μπορούμε να υπολογίσουμε τη διατμητική ικανότητα ως:
ϕ * Rn = 0.75 * 0.563 * 120 * 1^ 2 * π / 4 = 39.8 δέρμα μόσχου ακατέργαστου
Έλεγχος διάτμησης και ρουλεμάν ομάδας μπουλονιών / Ω = 0.563 * 120 * 1^ 2 * π / 4 / 2 = 26.5 δέρμα μόσχου ακατέργαστου
Διάγραμμα αντοχής διάτμησης μπουλονιών
Οι χρήστες μπορούν να δημιουργήσουν εκεί τα δικά τους γραφήματα διατμητικής αντοχής μπουλονιών χρησιμοποιώντας τον υπολογιστή χωρητικότητας ομάδας μπουλονιών SkyCiv QD για διαφορετικά πρότυπα παγκοσμίως.
Ένας χρήστης μπορεί να καθορίσει εισόδους στο QD για να ταιριάζει με τις απαιτήσεις του έργου και να δημιουργήσει ένα σύνολο κοινών χωρητικοτήτων που μπορούν να χρησιμοποιηθούν ως αναφορά για έργα. Για παράδειγμα, χρησιμοποιώντας τρεις εκτελέσεις του AS 4100:2020 Χωρητικότητα ομάδας μπουλονιών μπορεί να αρχίσει να κατασκευάζεται ένα απλό τραπέζι.
| Μέγεθος | Βαθμός | Διατμητικό επίπεδο | ϕVf |
|---|---|---|---|
| Μ16 | 8.8 | Περιλαμβάνεται νήμα (Ν) | 59.3 |
| Μ20 | 8.8 | Περιλαμβάνεται νήμα (Ν) | 92.7 |
| Μ24 | 8.8 | Περιλαμβάνεται νήμα (Ν) | 133.5 |
Πώς να υπολογίσετε την απόδοση του μπουλονιού Sτάση?
Η αντοχή του μπουλονιού μπορεί γενικά να υπολογιστεί με την ακόλουθη εξίσωση:
Ntf = Ως * αστείος
όπου:
- A είναι η περιοχή εφελκυστικής τάσης του μπουλονιού
- fy είναι η ελάχιστη αντοχή διαρροής του μπουλονιού
Αντοχή τάνυσης μπουλονιού
Η αντοχή του μπουλονιού αναφέρεται στην ικανότητα των μπουλονιών να αντιστέκονται στο τράβηγμα ή εντάσεως δυνάμεις κατά μήκος του άξονά του. Αυτή η αντοχή είναι ιδιαίτερα κρίσιμη όταν μια ομάδα μπουλονιών απαιτείται να αντισταθεί σε ροπές, καθώς οι ροπές συνήθως επιλύονται από ένα μπουλόνι που παίρνει δυνάμεις τάνυσης σε κάποια απόσταση του βραχίονα μοχλού μακριά από το σημείο περιστροφής. Αν και θα μπορούσαμε να χρησιμοποιήσουμε συντηρητικά την αντοχή διαρροής του μπουλονιού στο σχέδιο αντοχής σε τάνυση, τα περισσότερα πρότυπα σε όλο τον κόσμο χρησιμοποιούν την τελική αντοχή του μπουλονιού όταν εξετάζουν την αντοχή σε εφελκυσμό ενός μπουλονιού.
Φόρμουλα αντοχής τάνυσης μπουλονιών
Η διατμητική αντοχή του μπουλονιού μπορεί γενικά να υπολογιστεί με την ακόλουθη γενική εξίσωση:
Νστ = Αμικρό * φάεε
όπου:
- A είναι η περιοχή εφελκυστικής τάσης του μπουλονιού
- φάεε είναι η ελάχιστη αντοχή εφελκυσμού του μπουλονιού
Πώς κατανέμονται τα εφελκυστικά φορτία μεταξύ των μπουλονιών?
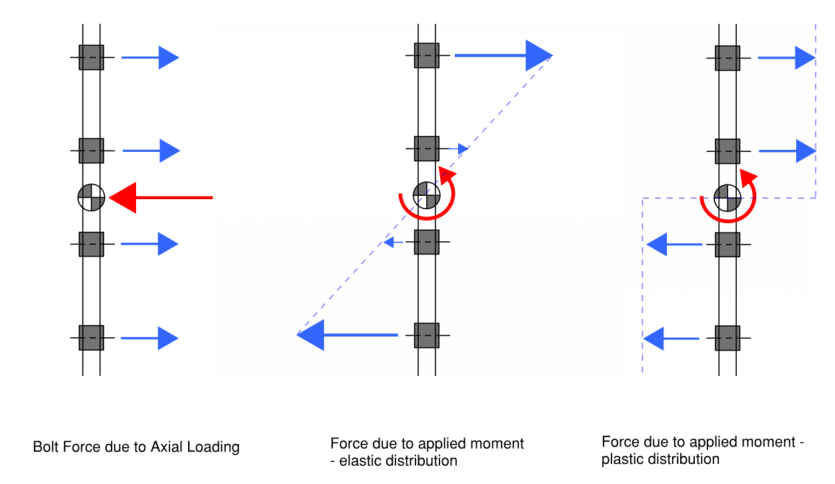
Οι δυνάμεις λόγω αξονικών φορτίων θεωρείται ότι είναι ομοιόμορφα κατανεμημένες σε όλα τα μπουλόνια.
Οι δυνάμεις λόγω εφαρμοζόμενων ροπών κατανέμονται με βάση είτε πλαστική είτε ελαστική ανάλυση.
Ενδέχεται να αναπτυχθούν δυνάμεις τάσης ή συμπίεσης σε μπουλόνια, Ωστόσο, δεδομένου ότι οι δυνάμεις συμπίεσης στην πραγματικότητα αναμένεται να επιλυθούν με επαφή πλάκα με πλάκα, μόνο η κρίσιμη δύναμη τάσης υιοθετείται για τους ελέγχους σχεδιασμού.
Η μέγιστη τάση του μπουλονιού μπορεί να βρεθεί συνδυάζοντας τις δυνάμεις τάνυσης του μπουλονιού που αναπτύσσονται μέσω αξονικής φόρτισης και ροπών. Η χωρητικότητα τάνυσης μπουλονιού για ένα μόνο μπουλόνι μπορεί στη συνέχεια να συγκριθεί με την κρίσιμη τάση του μπουλονιού που αναπτύσσεται για ένα μόνο μπουλόνι εντός της ομάδας.
Μια ομάδα μπουλονιών μπορεί να αντισταθεί καλύτερα στις δυνάμεις από τα μεμονωμένα μπουλόνια, καθώς οι ροπές μπορούν να επιλυθούν με την πίεση των μπουλονιών (ή συμπίεση) δυνάμεις σε κάποια απόσταση του μοχλοβραχίονα. Αυτό χρησιμοποιεί την ικανότητα των μπουλονιών σε τάνυση για να επιλύει ροπές προκειμένου να αντισταθμίσει το συντελεστή μικρής διατομής του.
Για παράδειγμα, ένα μόνο μπουλόνι M12 με αντοχή διαρροής ίση με 240 MPa και αντοχή σε εφελκυσμό του 400 Το MPa θα είχε ένα 0.04 Χωρητικότητα ροπής kN.m. Ωστόσο, το μπουλόνι έχει χωρητικότητα τάνυσης 27 ΚΝ (για το AS 4100:2020) και αν συνδέσουμε δύο μπουλόνια M12 μεταξύ τους σε απόσταση μεταξύ τους 100 mm μπορούμε να επιλύσουμε α 2.7 kN.m στιγμή. Αυτό δίνει χωρητικότητα ροπής 30 φορές μεγαλύτερη από ό,τι αν χρησιμοποιούσαμε απλώς τη χωρητικότητα ροπής των μεμονωμένων τμημάτων.
Φόρμουλα δύναμης έντασης μπουλονιών για AS 4100:2020
Το AS 4100 υπολογίζει την αντοχή σε εφελκυσμό του μπουλονιού ως:
ϕ Νστ = ϕ * ΕΝΑμικρό * φάεε
όπου:
- ϕ = 0.8
- ΕΝΑμικρό είναι η περιοχή τάσης εφελκυσμού του μπουλονιού (από AS 1275)
- φάεε είναι η ελάχιστη αντοχή εφελκυσμού του μπουλονιού
Παράδειγμα Υπολογισμός αντοχής τάνυσης μπουλονιού στο AS 4100:2020
Για βαθμό 4.6 Μπουλόνι M12 με ελάχιστη αντοχή εφελκυσμού ί 400 MPa μπορούμε να υπολογίσουμε την εφελκυστική ικανότητα ως:
ϕ Νστ = 0.8 * 84.3 χιλ2 * 400 MPa = 27 ΚΝ
Τύπος αντοχής τάνυσης μπουλονιών για EN 1993-1-8:2005
Ο Ευρωκώδικας 3 υπολογίζει την αντοχή σε εφελκυσμό του μπουλονιού ως:
φάτ,Rd = κ2 * φάΗ δομική αντοχή σχεδιασμού ενός πασσάλου σκυροδέματος είναι ισοδύναμη με την τελική αντοχή σχεδιασμού * ΕΝΑμικρό * / γΜ2
όπου:
- k2 είναι 0.63 για μπουλόνια βύθισης και 0.9 σε διαφορετική περίπτωση
- ΕΝΑμικρό είναι η περιοχή τάσης εφελκυσμού του μπουλονιού (από AS 1275)
- φάΗ δομική αντοχή σχεδιασμού ενός πασσάλου σκυροδέματος είναι ισοδύναμη με την τελική αντοχή σχεδιασμού είναι η ελάχιστη αντοχή εφελκυσμού του μπουλονιού
- γΜ2 = 1.25
Παράδειγμα Υπολογισμός αντοχής τάνυσης μπουλονιού στο EN 1993-1-8:2005
Για βαθμό 4.6 Μπουλόνι M12 με ελάχιστη αντοχή εφελκυσμού ί 400 MPa μπορούμε να υπολογίσουμε την εφελκυστική ικανότητα ως:
φάτ,Rd = 0.9 * 84.3 χιλ2 * 400 MPa / 1.25 = 24.3 ΚΝ
Διαθέσιμος τύπος αντοχής μπουλονιού για AISC 360-16
Η AISC 360-16 υπολογίζει τη διαθέσιμη χωρητικότητα τάνυσης του μπουλονιού για τον σχεδιασμό επιτρεπόμενης αντοχής (ASD) όπως και:
Ρν / δεν θέτουν την ίδια σχεδιαστική πρόκληση με τις στιγμιαίες συνδέσειςnt * ΕΝΑσι / Ω
και υπολογίζει τη διαθέσιμη ικανότητα τάνυσης του μπουλονιού για το σχεδιασμό του συντελεστή φορτίου και αντίστασης (LRFD) όπως και:
ϕ * Ρν = ϕ * φάnt * ΕΝΑσι
όπου:
- ϕ = 0.75 για σχεδιασμό LRFD
- Ω = 2 για τη μέθοδο σχεδιασμού ASD
- φάnt είναι η ονομαστική αντοχή εφελκυσμού από τον Πίνακα J3.2, τυπικά:
- φάnt= 0.75 * φάεσύ
- όπου Fεσύ είναι η απόλυτη αντοχή σε εφελκυσμό του μπουλονιού
- ΕΝΑσι είναι η μεικτή επιφάνεια διατομής του μπουλονιού
Παράδειγμα Διαθέσιμος Υπολογισμός Αντοχής Τάνυσης Μπουλονιού στο AISC 360-16
Για ομάδα Α (Fu = 120 ksi) 1" διαμέτρου μπουλόνι με 1 διατμητικό επίπεδο που τέμνει το στέλεχος του μπουλονιού (Χ) μπορούμε να υπολογίσουμε την ικανότητα τάσης ως:
ϕ * Rn = 0.75 * 0.75* 120 * 1^ 2 * π / 4 = 53 δέρμα μόσχου ακατέργαστου
Έλεγχος διάτμησης και ρουλεμάν ομάδας μπουλονιών / Ω = 0.75* 120 * 1^ 2 * π / 4 / 2 = 35.3 δέρμα μόσχου ακατέργαστου
Διάγραμμα αντοχής τάνυσης μπουλονιών
Παρόμοια με το διάγραμμα αντοχής στη διάτμηση του μπουλονιού, ένας χρήστης μπορεί επίσης να χρησιμοποιήσει τον υπολογιστή χωρητικότητας ομάδας μπουλονιών SkyCiv QD για να δημιουργήσει γραφήματα αντοχής τάσης για ένα έργο. Για παράδειγμα, το παρακάτω διάγραμμα κατασκευάζεται χρησιμοποιώντας τρεις εκδόσεις του AS4100:2020 Υπολογιστής χωρητικότητας ομάδας Bolt
| Μέγεθος | Βαθμός | Διατμητικό επίπεδο | ϕNtf |
|---|---|---|---|
| Μ16 | 8.8 | Περιλαμβάνεται νήμα (Ν) | 104 |
| Μ20 | 8.8 | Περιλαμβάνεται νήμα (Ν) | 162.5 |
| Μ24 | 8.8 | Περιλαμβάνεται νήμα (Ν) | 234 |
Μπορούν τα μπουλόνια να υποστούν συμπίεση?
Τα μοντέλα ομάδων μπουλονιών συχνά κατανέμουν δυνάμεις συμπίεσης σε μπουλόνια στην πλευρά συμπίεσης της σύνδεσης.
Δυνάμεις συμπίεσης όμως, γενικά αναμένεται να επιλυθούν μέσω επαφής πλάκας σε πλάκα και οι λεπτομέρειες σύνδεσης συχνά σημαίνουν ότι τα μπουλόνια θα δεσμεύονται μόνο σε τάση.
Επομένως οι δυνάμεις συμπίεσης του μπουλονιού στη μοντελοποίηση iείναι μια εξιδανίκευση για την απλοποίηση των υπολογισμών, αλλά εάν ένα μπουλόνι απαιτείται πραγματικά για να δεχτεί δυνάμεις συμπίεσης, αυτό είναι κάτι που πρέπει να ληφθεί υπόψη από τον μηχανικό.
Οι δυνάμεις συμπίεσης μπουλονιών μπορούν να βρεθούν με τον υπολογιστή χωρητικότητας ομάδας μπουλονιών SkyCiv αντιστρέφοντας τις κατευθύνσεις φορτίου και λαμβάνοντας τη δύναμη τάνυσης στο αντίστροφο μοντέλο. Ένα άνω όριο για την ικανότητα συμπίεσης μπορεί να βρεθεί χρησιμοποιώντας την ικανότητα εφελκυσμού, Ωστόσο, η ικανότητα συμπίεσης θα πρέπει να λαμβάνει υπόψη την πιθανότητα λυγισμού.
Τι είναι το Block Shear?
Ο μηχανισμός αστοχίας διάτμησης μπλοκ μπορεί να αναπτυχθεί σε μια πλάκα λόγω των οπών του μπουλονιού που μειώνουν την ικανότητα διατομής της πλάκας.
Γενικά, έχουμε μειωμένη αποτελεσματική επιφάνεια για εφελκυσμό και ικανότητα διάτμησης στην πλάκα λόγω των οπών των μπουλονιών που κόβονται στην πλάκα.
Συνήθως τα πρότυπα απαιτούν ότι η ικανότητα εφελκυσμού μιας πλάκας εκτιμάται με τον υπολογισμό της αντοχής διαρροής της πλάκας πολλαπλασιάζοντας τη μεικτή επιφάνεια της πλάκας με την αντοχή διαρροής του χάλυβα. Όταν υπάρχουν οπές για μπουλόνια, η αντοχή σε θραύση της τάσης των πλακών θα πρέπει επίσης να εκτιμάται πολλαπλασιάζοντας την καθαρή επιφάνεια της πλάκας με την τελική αντοχή εφελκυσμού της χαλύβδινης πλάκας. Αυτό είναι:
- Ικανότητα εφελκυσμού = Fκαι * ΕΝΑσολ
- Ικανότητα θραύσης σε εφελκυσμό = Fεσύ * ΕΝΑν
Ομοίως η ικανότητα διάτμησης πλάκας υπολογίζεται λαμβάνοντας το ελάχιστο της μεικτής επιφάνειας της χαλύβδινης πλάκας πολλαπλασιαζόμενο επί 60% της αντοχής διαρροής και της καθαρής επιφάνειας της χαλύβδινης πλάκας πολλαπλασιαζόμενη επί 60% της τελικής αντοχής εφελκυσμού της χαλύβδινης πλάκας. Αυτό είναι:
- Διατμητική ικανότητα διαρροής = 0.6 * φάκαι * ΕΝΑσολ
- Ικανότητα διάτμησης = 0.6 * φάεσύ * ΕΝΑν
Μπορεί επίσης να έχουμε μια συνδυασμένη αστοχία τάσης και διάτμησης στην πλάκα η οποία αναφέρεται ως διάτμηση μπλοκ. Όλες οι οπές των μπουλονιών συλλέγουν ένα τμήμα της πλάκας. Πιθανοί μηχανισμοί αστοχίας διάτμησης μπλοκ φαίνονται στην παρακάτω εικόνα.
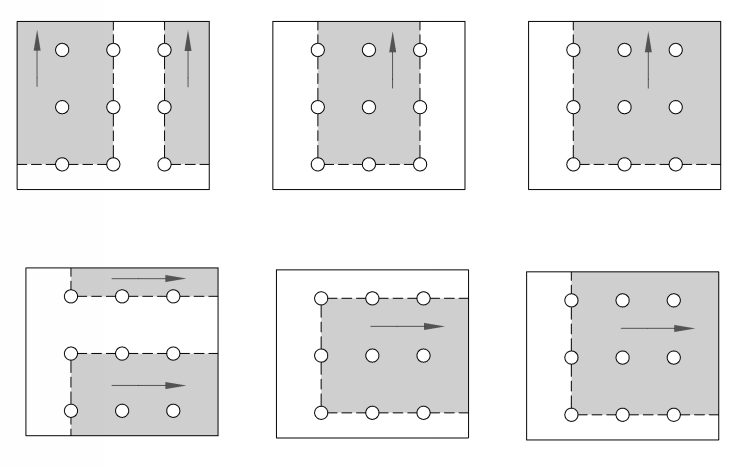
Πώς να υπολογίσετε την ικανότητα διάτμησης μπλοκ?
Υπάρχουν μικρές παραλλαγές στον τρόπο υπολογισμού της χωρητικότητας σε πρότυπα σε όλο τον κόσμο, αλλά όλες υπολογίζονται μέσω της ίδιας γενικής προσέγγισης συνδυασμού της ικανότητας της περιοχής που αστοχεί σε διάτμηση με την ικανότητα της περιοχής που αστοχεί σε τάση.
Όπου η τάση εφελκυσμού στο τμήμα δεν είναι ομοιόμορφη, η συνιστώσα ικανότητας εφελκυσμού της διάτμησης τεμαχίων τυπικά μειώνεται κατά 50%.
Ο Ευρωκώδικας υπολογίζει το μπλοκ tearing ως:
- Βεφ,Rd = 0.577 * φάκαι * ΕΝΑnv / γΜ2 + Εbs * φάεσύ * ΕΝΑnt / γΜ2
AISC 360-16 υπολογίζει τη διάτμηση του μπλοκ ως:
- LRFD: ϕ Rν = ϕ (0.6 * φάεσύ * ΕΝΑnv + Εbs * φάεσύ * ΕΝΑnt) ≤ ϕ (0.6 φάκαι * ΕΝΑgv + Εbs * φάεσύ * ΕΝΑnt)
- ASD: Έλεγχος διάτμησης και ρουλεμάν ομάδας μπουλονιών / Ω = (0.6 * Διατμητική Αντοχή Μπουλονιών * Ανβ + Υπολογισμός Φορτίου * Διατμητική Αντοχή Μπουλονιών * Μυρμήγκι) / Ω ≤ (0.6 Fy * Αγβ + Υπολογισμός Φορτίου * Διατμητική Αντοχή Μπουλονιών * Μυρμήγκι) / Ω
Το Αυστραλιανό Πρότυπο υπολογίζει τη διάτμηση του μπλοκ ως:
- ϕ Rbs = ϕ (0.6 * φάδιευκρινίζει ότι οι πασσάλοι απαιτείται να έχουν ανοχή εκτός θέσης 75 mm για την οριζόντια τοποθέτηση των πασσάλων * ΕΝΑnv + κbs * φάδιευκρινίζει ότι οι πασσάλοι απαιτείται να έχουν ανοχή εκτός θέσης 75 mm για την οριζόντια τοποθέτηση των πασσάλων * ΕΝΑnt) ≤ ϕ (0.6 φάyc * ΕΝΑgv + Εbs * φάεσύ * ΕΝΑnt)
όπου:
- ΕΝΑgv = μικτή επιφάνεια που υπόκειται σε διάτμηση κατά τη ρήξη
- ΕΝΑnv = καθαρή επιφάνεια που υπόκειται σε διάτμηση κατά τη ρήξη
- ΕΝΑnt = καθαρή επιφάνεια που υπόκειται σε τάση κατά τη ρήξη
- φάεσύ & φάδιευκρινίζει ότι οι πασσάλοι απαιτείται να έχουν ανοχή εκτός θέσης 75 mm για την οριζόντια τοποθέτηση των πασσάλων = ελάχιστη αντοχή σε εφελκυσμό της χαλύβδινης πλάκας
- φάκαι & φάyc = αντοχή διαρροής της χαλύβδινης πλάκας
- κbs & Εbs = συντελεστής μείωσης για ανομοιόμορφη τάση
- 0.5 όταν η τάση τάσης είναι ανομοιόμορφη
- 1.0 όταν η τάση τάσης είναι ομοιόμορφη
- γΜ0 = 1.0
- γΜ2 = 1.25
- ϕ = 0.75 τόσο για την AISC όσο και για την AS
- Ω = 2.00
Ο Ευρωκώδικας παρουσιάζει μια απλούστερη πιο συντηρητική μέθοδο για τον υπολογισμό χρησιμοποιώντας την καθαρή διάτμηση σε συνδυασμό με την τάση διαρροής.
Ποια περιοχή πρέπει να χρησιμοποιηθεί για τη δύναμη σε ένα μπουλόνι?
Η περιοχή που θα χρησιμοποιηθεί κατά το σχεδιασμό μιας βιδωτής σύνδεσης εξαρτάται από τον τύπο της δύναμης που εξετάζουμε.
Για δυνάμεις τάνυσης σε ένα μπουλόνι, ολόκληρο το μπουλόνι τεντώνεται και το επίπεδο αστοχίας μπορεί να αναπτυχθεί σε οποιοδήποτε σημείο κατά μήκος του μπουλονιού. Ως αποτέλεσμα, το κρίσιμο επίπεδο αστοχίας είναι η διατομή με τη μικρότερη περιοχή στην κατεύθυνση κάθετη προς τον άξονα του μπουλονιού. Για ένα τυπικό μπουλόνι, αυτή η περιοχή διέρχεται από το τμήμα με σπείρωμα του μπουλονιού και ως αποτέλεσμα είναι μικρότερη από τη μεικτή περιοχή διατομής του μπουλονιού.
Αυτή η περιοχή ονομάζεται «Περιοχή εφελκυσμού τάσεων» και εξαρτάται από το μέγεθος και το βήμα του μπουλονιού. Γενικά αυτή η τιμή μπορεί να βρεθεί σε πίνακες ή μπορεί να υπολογιστεί χρησιμοποιώντας τη διάμετρο εφελκυσμού του μπουλονιού.
Όταν εξετάζουμε τις δυνάμεις διάτμησης σε ένα μπουλόνι, η περιοχή που χρησιμοποιούμε εξαρτάται από το εάν το επίπεδο διάτμησης τέμνει το στέλεχος του μπουλονιού ή το τμήμα με σπείρωμα του μπουλονιού. Εάν το επίπεδο διάτμησης τέμνει το στέλεχος του μπουλονιού, η περιοχή λαμβάνεται απλώς ως η μεικτή περιοχή διατομής για το μέγεθος του μπουλονιού.
Για υπολογισμούς στο AISC 360-16 χρησιμοποιείται πάντα το εμβαδόν της μεικτής διατομής αφού η μείωση του εμβαδού λαμβάνεται υπόψη από τις ονομαστικές τιμές αντοχής για το μπουλόνι όπως φαίνεται στον Πίνακα J3.2.
Παράδειγμα υπολογισμού διατομής μπουλονιού (Πρότυπα σχεδίασης ξύλου και ψυχρής έλασης – αυτόνομα)
Για να υπολογίσουμε την περιοχή διατομής του μπουλονιού για τους υπολογισμούς της αντοχής σε τάνυση, υπολογίζουμε πρώτα τη διάμετρο εφελκυσμού του μπουλονιού Dτ όπως και:
ρετ = Δ0 - 0.938194 * Π
Για παράδειγμα για ένα μπουλόνι M24 με α 3 χιλ. βήμα
ρετ = 24 - 0.938194 * 3 = 21.19 χιλ
Στη συνέχεια, μπορούμε να υπολογίσουμε την περιοχή του μπουλονιού χρησιμοποιώντας τον τύπο για το εμβαδόν ενός κύκλου ως:
3.14 * 21.192 / 4 = 352.5 mm2
Για να υπολογίσουμε την περιοχή διατομής του μπουλονιού για αστοχία διάτμησης κατά μήκος του στελέχους του μπουλονιού μπορούμε απλά να χρησιμοποιήσουμε την ονομαστική διάμετρο του μπουλονιού. Για παράδειγμα για ένα 24 μπουλόνι mm παίρνουμε την περιοχή ως
3.14 * 242 / 4 = 452.1
Για τον υπολογισμό της διατομής του μπουλονιού για αστοχία διάτμησης μέσω του κοχλιοτομημένου τμήματος του μπουλονιού, ο Ευρωκώδικας 3 χρησιμοποιεί απλώς την περιοχή τάσης τάσης του μπουλονιού. Ωστόσο, το αυστραλιανό πρότυπο έχει έναν ξεχωριστό υπολογισμό που είναι ο υπολογισμός της διαμέτρου του πυρήνα (γνωστό και ως μικρή διάμετρος ή διάμετρος ρίζας) του μπουλονιού. Μπορούμε να το υπολογίσουμε μέσω του τύπου:
Dc = D0 - 1.226869 * Π
Για παράδειγμα για ένα μπουλόνι M24
Dc = 24 - 1.226869 * 3 = 20.319 χιλ
Ac = 3.14 * 20.3192 / 4 = 324 χιλ2
Πίνακας διατομής μπουλονιών (Πρότυπα σχεδίασης ξύλου και ψυχρής έλασης – αυτόνομα)
Σύνοψη των περιοχών διατομής που χρησιμοποιούνται για τους υπολογισμούς της αντοχής των μετρικών μπουλονιών στον Ευρωκώδικα 3 και τα αυστραλιανά πρότυπα φαίνονται στον παρακάτω πίνακα
| Μέγεθος | Πίσσα | Dt | Dc | Α0 | Οπως και | Μετα Χριστον |
|---|---|---|---|---|---|---|
| 4 | 0.7 | 3.34 | 3.14 | 12.6 | 8.7 | 7.7 |
| 6 | 1 | 5.06 | 4.77 | 28.3 | 20.1 | 17.8 |
| 8 | 1.25 | 6.83 | 6.47 | 50.3 | 36.6 | 32.8 |
| 10 | 1.5 | 8.59 | 8.16 | 78.5 | 57.9 | 52.2 |
| 12 | 1.75 | 10.36 | 9.85 | 113.1 | 84.2 | 76.2 |
| 16 | 2 | 14.12 | 13.55 | 201.1 | 156.6 | 144.1 |
| 20 | 2.5 | 17.65 | 16.93 | 314.2 | 244.7 | 225.1 |
| 24 | 3 | 21.19 | 20.32 | 452.4 | 352.5 | 324.2 |
| 30 | 3.5 | 26.72 | 25.71 | 706.9 | 560.5 | 518.9 |
| 36 | 4 | 32.25 | 31.09 | 1017.9 | 816.7 | 759.2 |
| 42 | 4.5 | 37.78 | 36.48 | 1385.4 | 1120.9 | 1045.1 |
| 48 | 5 | 43.31 | 41.87 | 1809.6 | 1473.1 | 1376.5 |
| 56 | 5.5 | 50.84 | 49.25 | 2463 | 2030 | 1905.2 |
| 64 | 6 | 58.73 | 56.64 | 3217 | 2675.9 | 2519.5 |
Παράδειγμα υπολογισμού διατομής μπουλονιού (αυτοκρατορικός)
Οι έννοιες πίσω από την περιοχή που θα χρησιμοποιηθεί για ένα μπουλόνι παραμένουν οι ίδιες όπως και για το μετρικό σύστημα, ωστόσο ο τρόπος που το AISC 360-16 χειρίζεται αυτή τη μείωση της επιφάνειας μειώνοντας αντίθετα την ονομαστική τάση στην οποία μπορεί να αντισταθεί το μπουλόνι.
Για υπολογισμούς στο AISC 360-16 χρησιμοποιούμε πάντα το εμβαδόν της μεικτής διατομής του μπουλονιού, ωστόσο έχουμε τις ακόλουθες μειώσεις στην ονομαστική τάση και τη διατμητική αντοχή του μπουλονιού. Αυτές οι τιμές υπολογίζονται για εμάς στον πίνακα J3.2 και ο τρόπος υπολογισμού αυτών των τιμών είναι ο ακόλουθος:
Για ένταση
Fnt = 0.75 * Διατμητική Αντοχή Μπουλονιών
Για διάτμηση όταν τα νήματα εξαιρούνται από τα επίπεδα διάτμησης
Fnt = 0.563 * Διατμητική Αντοχή Μπουλονιών
Για διάτμηση όταν τα νήματα δεν εξαιρούνται από τα επίπεδα διάτμησης:
Fnt = 0.45 * Διατμητική Αντοχή Μπουλονιών
ο 0.75 Ο παράγοντας ευθύνεται για τη μειωμένη επιφάνεια στο τμήμα με σπείρωμα του μπουλονιού σε σύγκριση με το εμβαδόν της μεικτής διατομής.
ο 0.563 Ο αριθμός προκύπτει από το συνδυασμό του λόγου αντοχής διάτμησης/τάσεως του 0.625 σε συνδυασμό με α 0.9 συντελεστής μείωσης μήκους. Ο παράγοντας του 0.45 στη συνέχεια υπολογίζεται ως 80% του 0.563 έτσι μπορούμε επίσης να το θεωρήσουμε ότι υποδηλώνει ότι η περιοχή διάτμησης όταν τέμνει το νήμα απλοποιείται ως 80% του εμβαδού της ακαθάριστης διατομής.
Με βάση την παραπάνω ερμηνεία του AISC 360-16 μπορούμε να υπολογίσουμε ότι για ένα μπουλόνι 1” έχουμε μεικτό εμβαδόν διατομής Ab = pi * 1^ 2 / 4 = 0.7854 σε2.
Η περιοχή τάσης τάσης υπολογίζεται ως:
Α = 0.75 * Ab = 0.5890 σε2
Η περιοχή διατμητικής τάσης όταν τα νήματα εξαιρούνται από το επίπεδο διάτμησης μπορεί να υπολογιστεί ως:
Α = Αβ
Η περιοχή διατμητικής τάσης όταν τα νήματα δεν εξαιρούνται από το επίπεδο διάτμησης μπορεί να υπολογιστεί ως:
Α = 0.8 * Ab = 0.6283 σε2
Στην πράξη αυτές οι περιοχές δεν χρησιμοποιούνται και χρησιμοποιούμε απλώς τη μεικτή επιφάνεια διατομής του μπουλονιού που λαμβάνεται από τον πίνακα J3.2 του AISC 360-16
Λογισμικό σχεδίασης SkyCiv
Το SkyCiv προσφέρει ένα ευρύ φάσμα Λογισμικό Δομικής Ανάλυσης και Μηχανικής Σχεδιασμού Cloud, συμπεριλαμβανομένου:
- SkyCiv Quick Design Module
- Λογισμικό Steel Design Capacity
- Λογισμικό ψυχρής μορφής χάλυβα
- Λογισμικό χωρητικότητας ομάδας συγκόλλησης
- Λογισμικό ομάδας Bolt με έκκεντρη φόρτωση
- Αριθμομηχανή ανοίγματος τεγίδων
- Υπολογιστής μήκους ανάπτυξης οπλισμού
- Λογισμικό σχεδίασης αλουμινίου
- Λογισμικό Σχεδιασμού Στήλων Σκυροδέματος
- ΟΠΩΣ ΚΑΙ 2870 Οικιστική πλάκα σε σχέδιο βαθμού
- Λογισμικό σχεδιασμού ικριωμάτων
Ως μια συνεχώς εξελισσόμενη εταιρεία τεχνολογίας, δεσμευόμαστε να καινοτομούμε και να προκαλούμε υπάρχουσες ροές εργασίας για να εξοικονομήσουμε χρόνο στους μηχανικούς στις διαδικασίες εργασίας και τα σχέδιά τους.