不对称截面

不对称截面在垂直 y 轴或水平 z 轴上不对称或, 在某些情况下, 任意轴. 不对称截面的例子是角形和 Z 形截面.

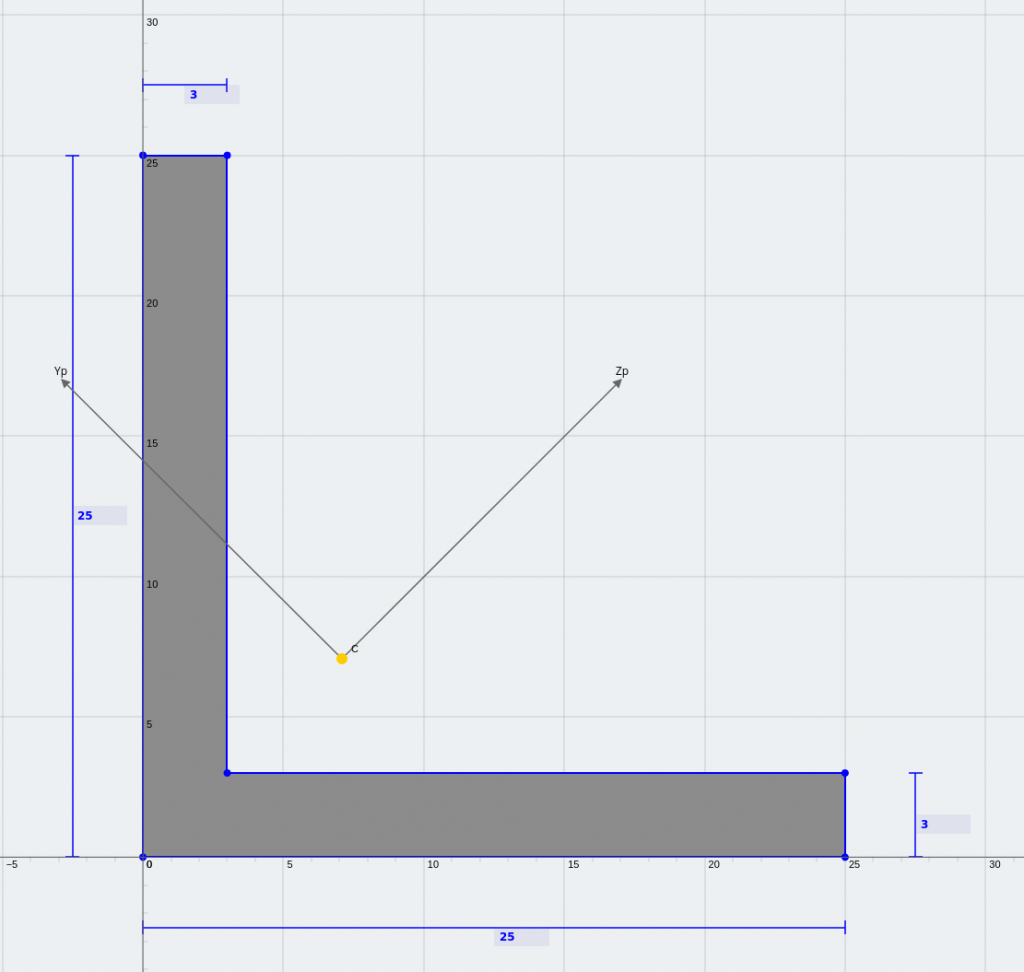
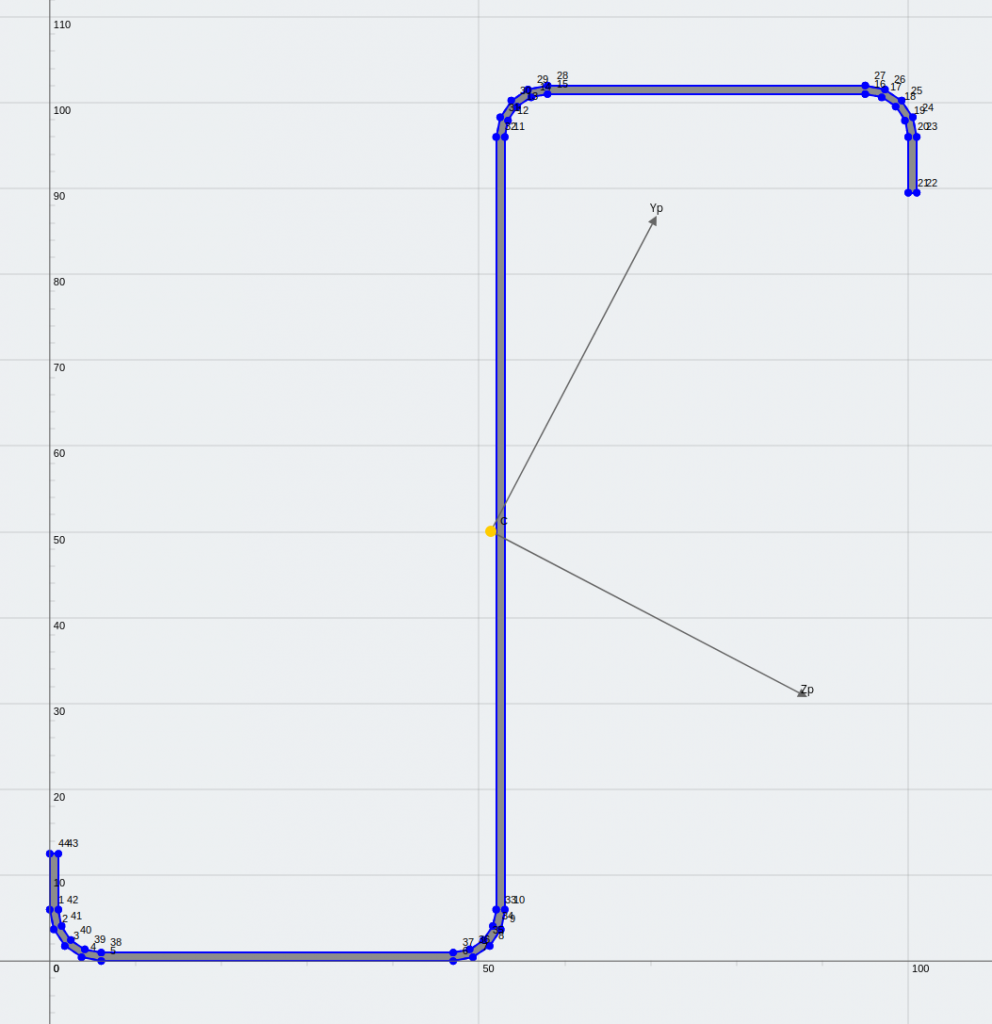
等角和唇形 Z 截面 (关于主轴镜像对称)

截面不对称的梁与弯曲双对称梁的行为不同. 即使梁在垂直轴上具有等效刚度，它的行为也不会像 RHS 而 I 形.

在这个例子中，我将用一个简单的负载情况来演示它们的行为: 垂直均布荷载.

分析

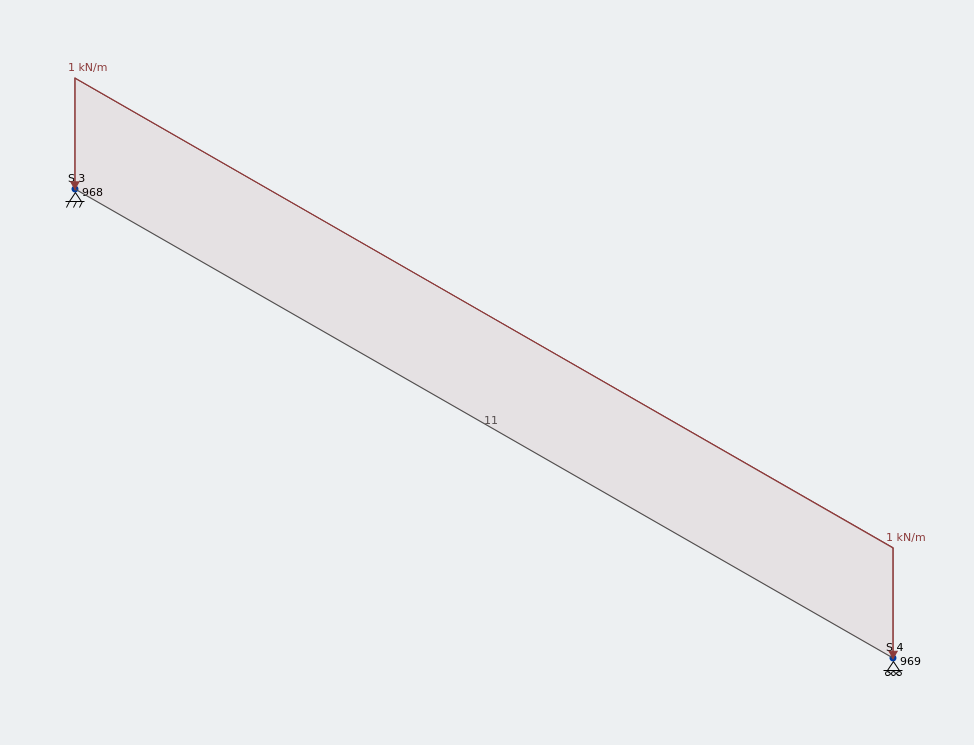
框架模型 1.5 m 在垂直 UDL 下的等角

我已经沿此的全长施加了 1kN/m 的均匀分布载荷 1.5 m 等角.

如果我想检查这个梁跨中的挠度，我可以很容易地. 我所需要的只是面积的第二个时刻, 及简支梁标准最大挠度公式. 使用 SkyCiv Section Builder 进行快速计算，我可以轻松获得截面属性.

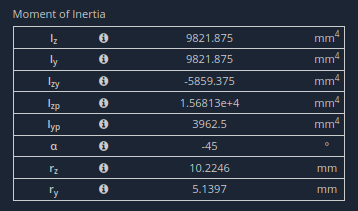
来自 SkyCiv Section Builder 的表格截面属性

伊兹是 9821.9 mm 的 4 次方. 截面是结构钢，E = 200 GPa.

看看当我在 SkyCiv Structural 3D 中使用 FEA 计算时会发生什么.

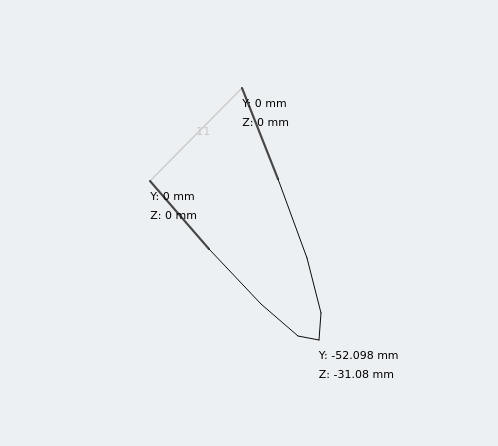
加载等角位移

等角截面有两个偏转分量! 使用先前的计算分析使用双对称截面的简支梁的挠度，这将是一种完全可以接受的快速检查方法. 但是对于不对称的部分，我们需要另一条信息.

角度α

请注意，在上面的部分属性中, α 的值不为零.

这意味着主轴不平行于几何轴之一.

演示旋转轴对计算出的刚度值的影响, 当坐标系旋转时，我在水平和垂直轴的刚度下方绘制.

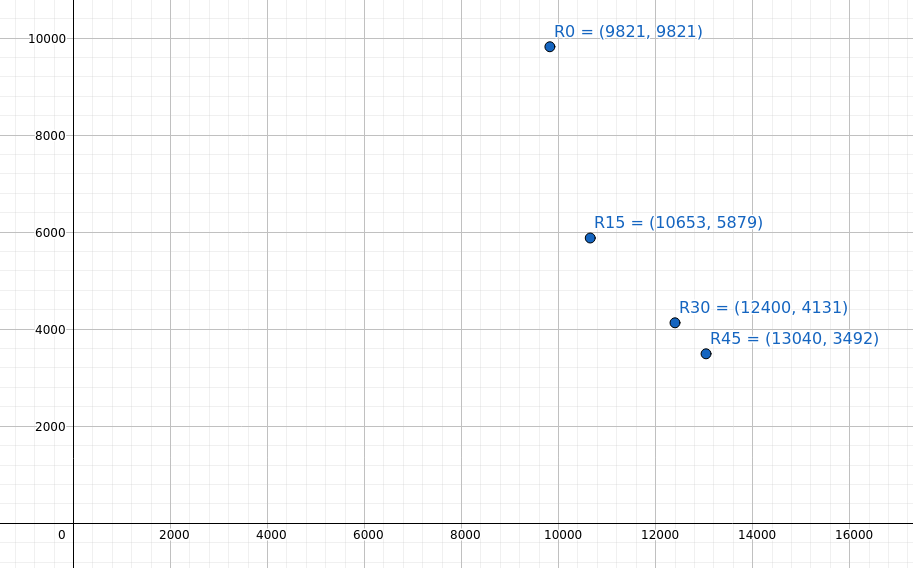
旋转坐标系后 25x25x3 EA 的刚度

注意随着坐标系旋转而形成的非线性曲线 15, 30 和 45 度数. 该曲线将是该部分独有的.

那么为什么会发生这种情况?

一位讲师曾经告诉我，载荷遵循结构中最坚硬的部分. 在这种情况下, 负载由最硬的轴承载 (主轴).

正确的做法

计算挠度结果的正确方法包括首先将所有载荷转换为主轴, 然后根据沿主轴的面积二阶矩计算挠度. 为了证明这确实是正确的方法，我使用手工计算验证了答案, 并使这更有趣, 使用框架元素的梁模型和, 用贝壳建造的模型. 这样就可以毫无疑问我们之前看到的位移确实是正确的.

这是我创建的模型.

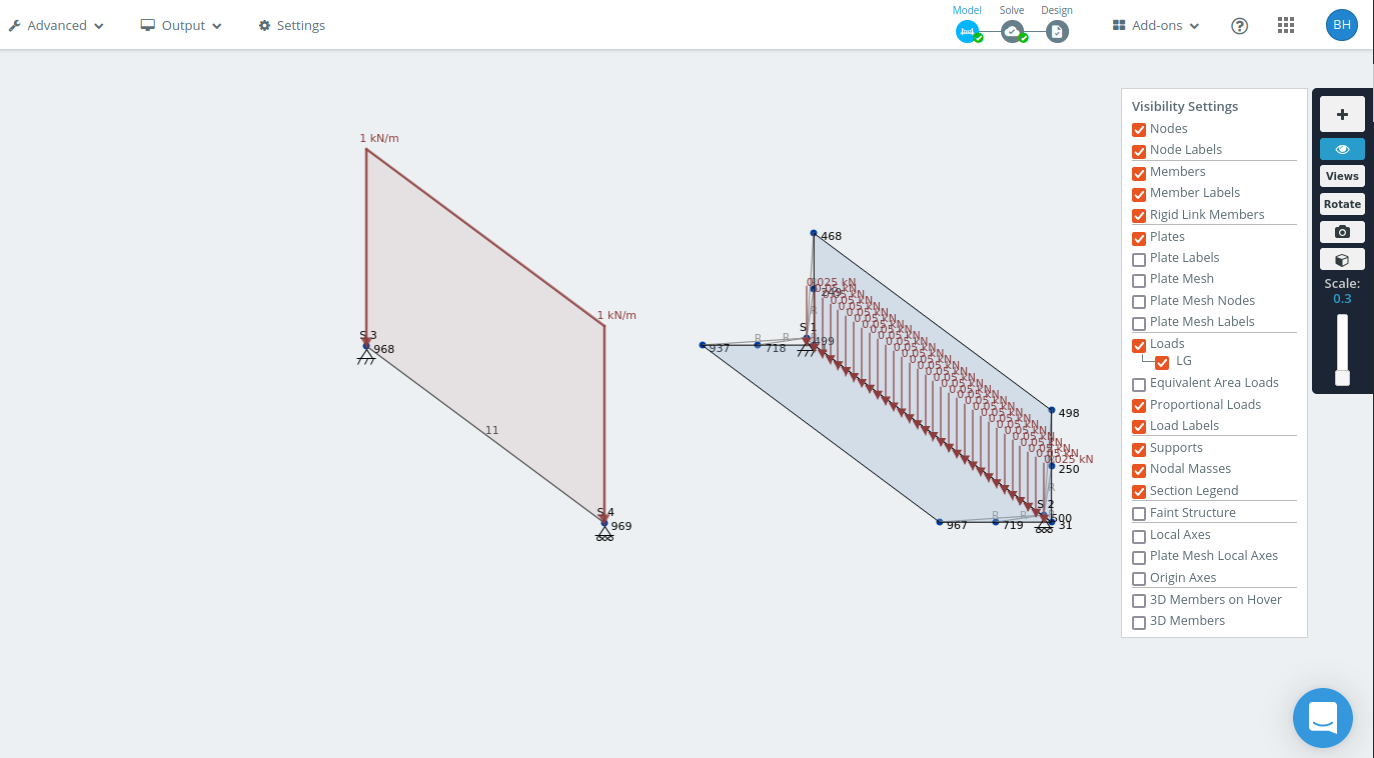
框架模型和外壳模型 1.5 米角

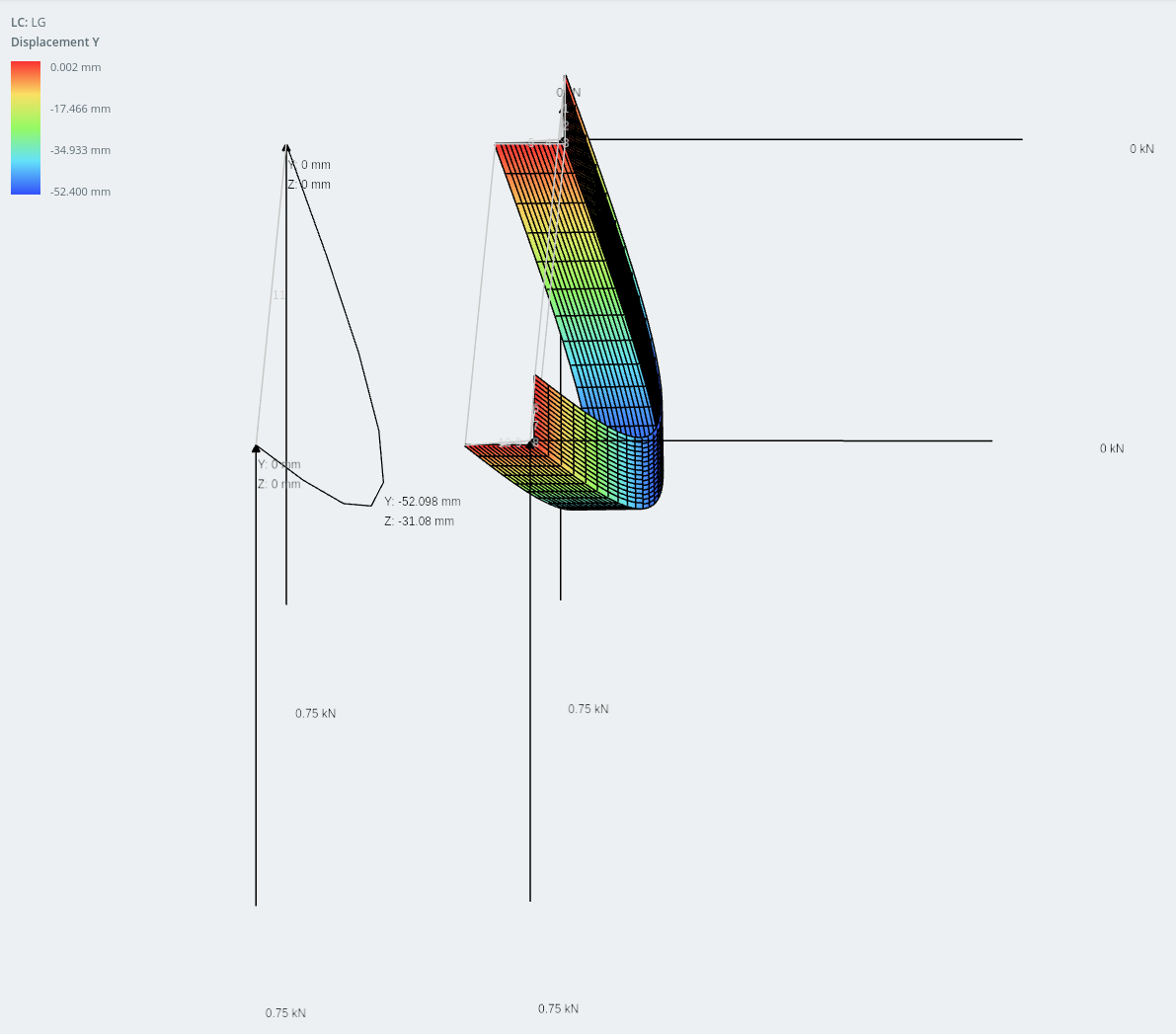
垂直方向的位移

两个模型的结果差异极其接近: 内 1% 彼此的.

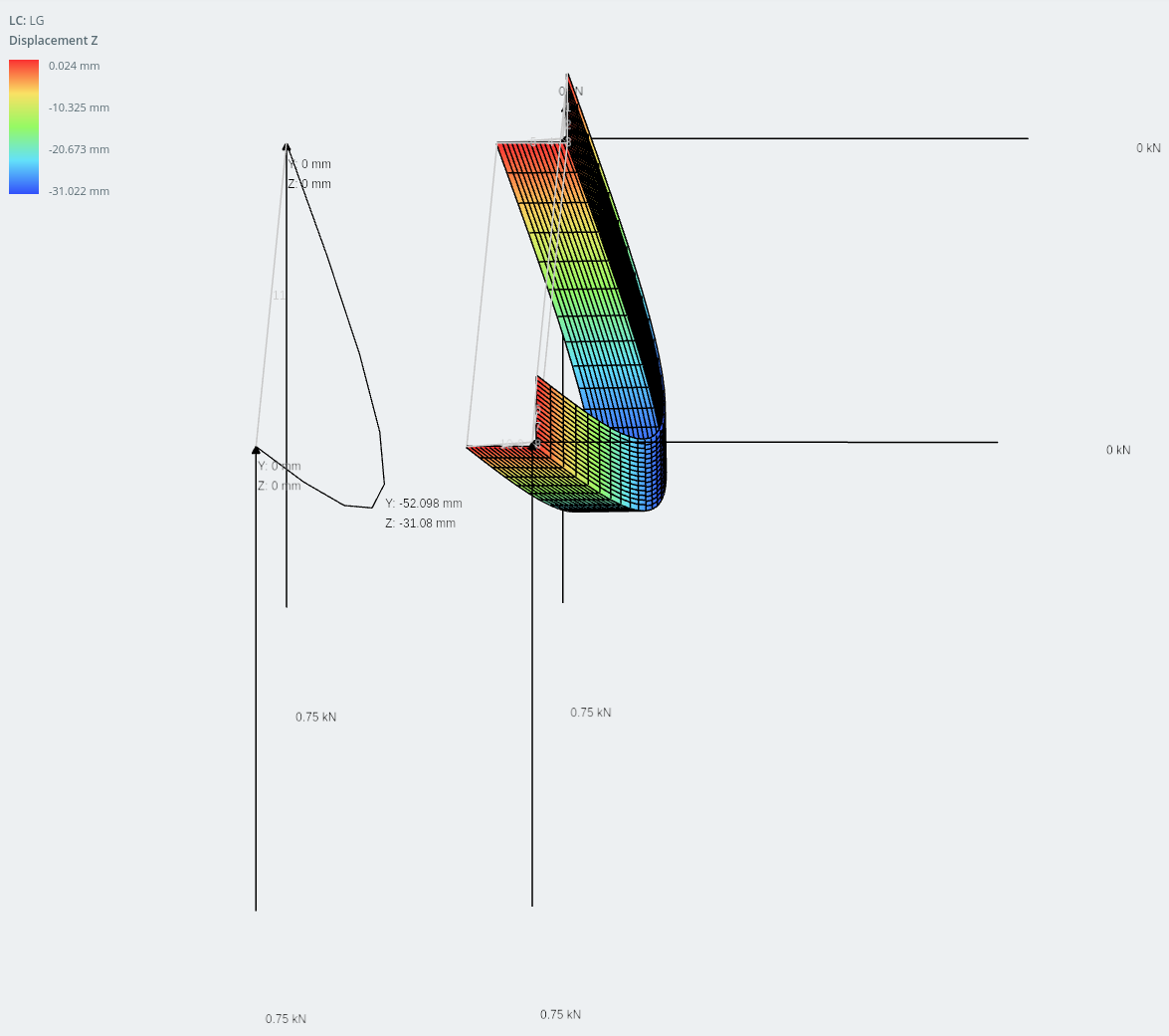
水平方向的位移.

它们通过下面的手工计算得到证实.

为什么要使用这些部分?

工程师喜欢设计轻便高效的结构, 但有时对结构组件的形式有限制, 通常是由于其他人的设计决定. 这种对形式的限制可能有多种原因, 可能是因为建筑师出于美学原因想要隐藏结构元素, 或遵守当地的规划法律. 可能是由于本地制造能力或仅仅是原材料的可用性和成本而存在限制. 制造成本和涂层也可能发挥重要作用. 有时, 我们被我们所拥有的困住了.

有选择的时候, 可能会选择该部分，因为它具有某些优势. 以 Z 部分为例, 常见的支撑倾斜压型钢板. 通常用于小倾斜屋顶角度, 通道更有效，因为重力载荷只引起关于弱轴的微小力矩. 这些力矩随着屋顶倾斜度的增加而增加，并且在一定的倾斜度下, Z 部分变得更高效.

为了演示，我将唇形 Z 截面建模为 1.5m 钢梁. 希望在看到移位的形状后，您能明白为什么它在通道上具有优势.

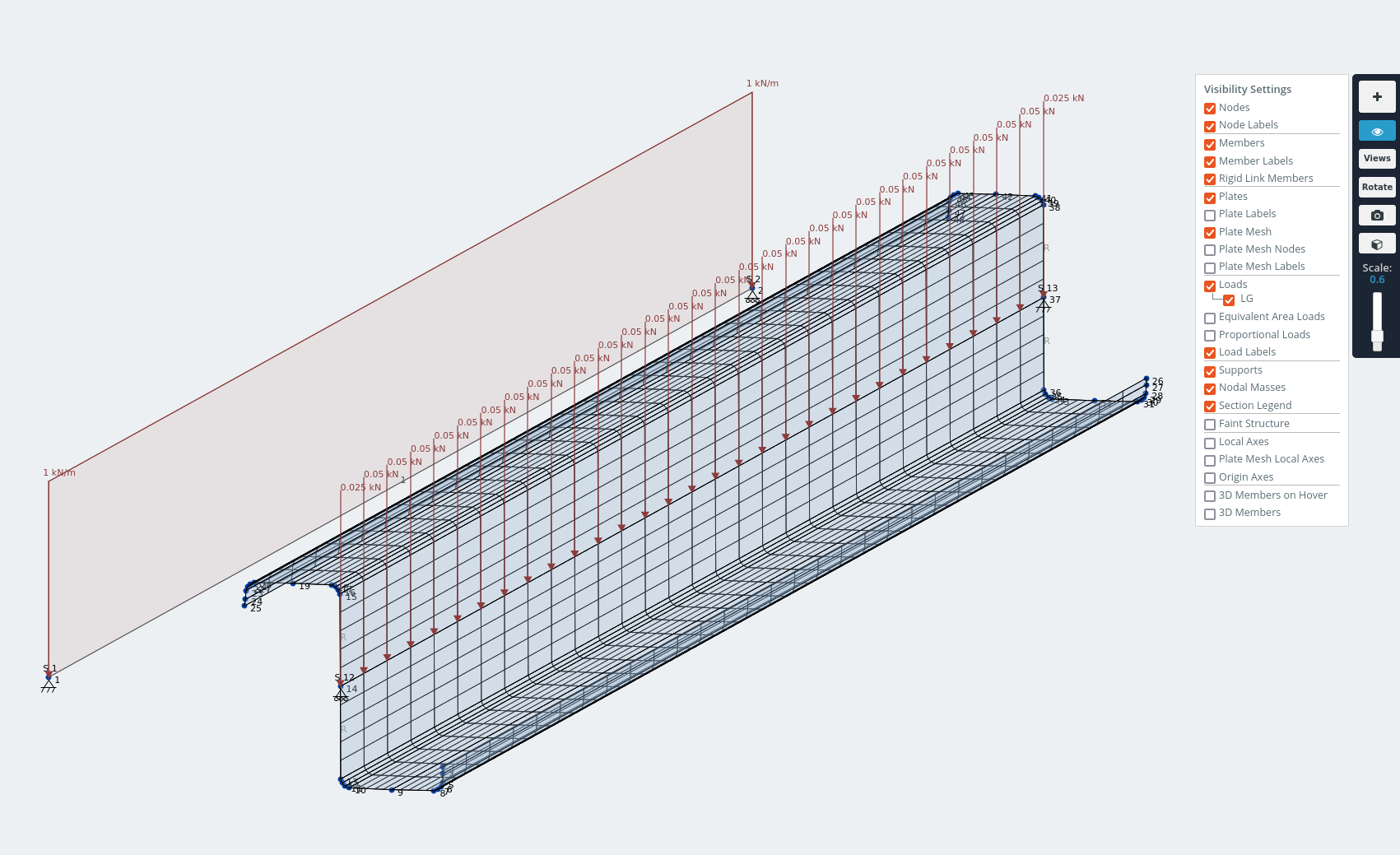
通过剪切中心施加 1kN/m 分布载荷的带唇 Z 截面模型.

z 轴上的位移与屋顶板在重力载荷下的平面内剪切作用相反.

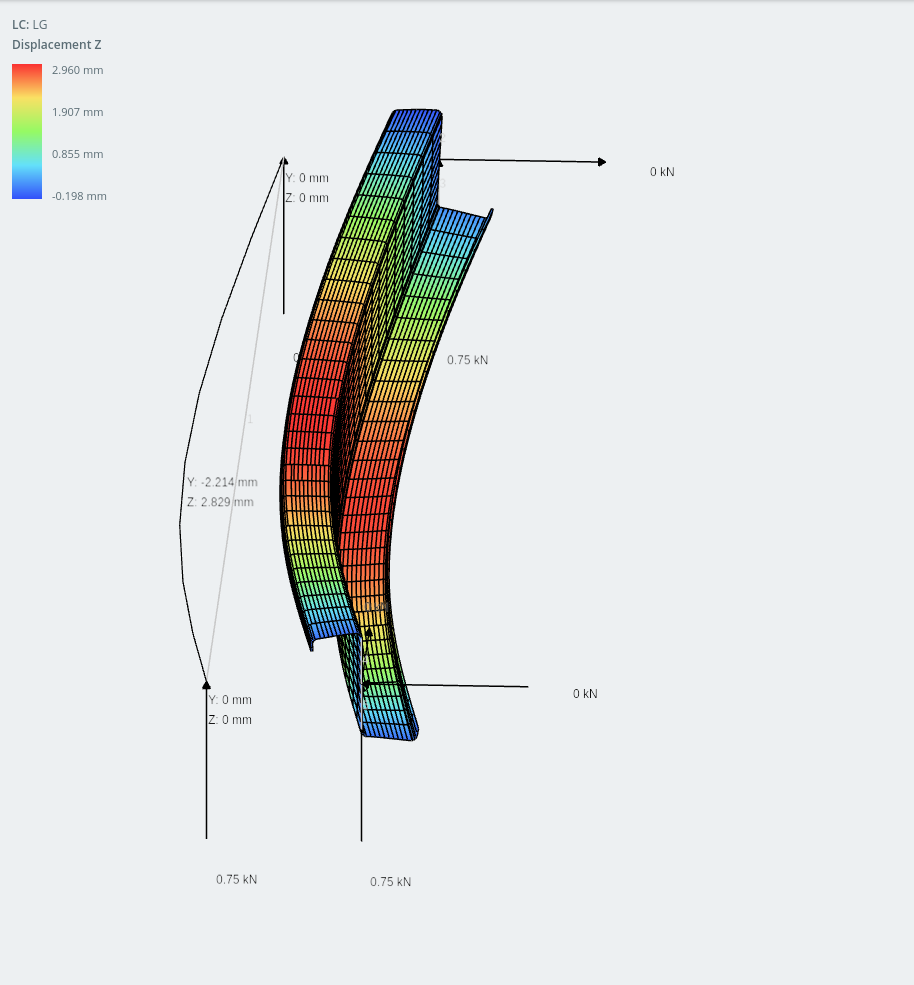
Lipped-Z截面框架模型和壳模型 (板上显示的水平位移)

惊人的, y 轴上的位移 (垂直) 实际上小于水平. 我必须承认我没想到会出现这种行为，但是使用现代冷成型技术，有很多有趣的方法可以优化截面以使其更轻, 更高效, 制造成本更低, 在施工过程中更容易组装和处理!

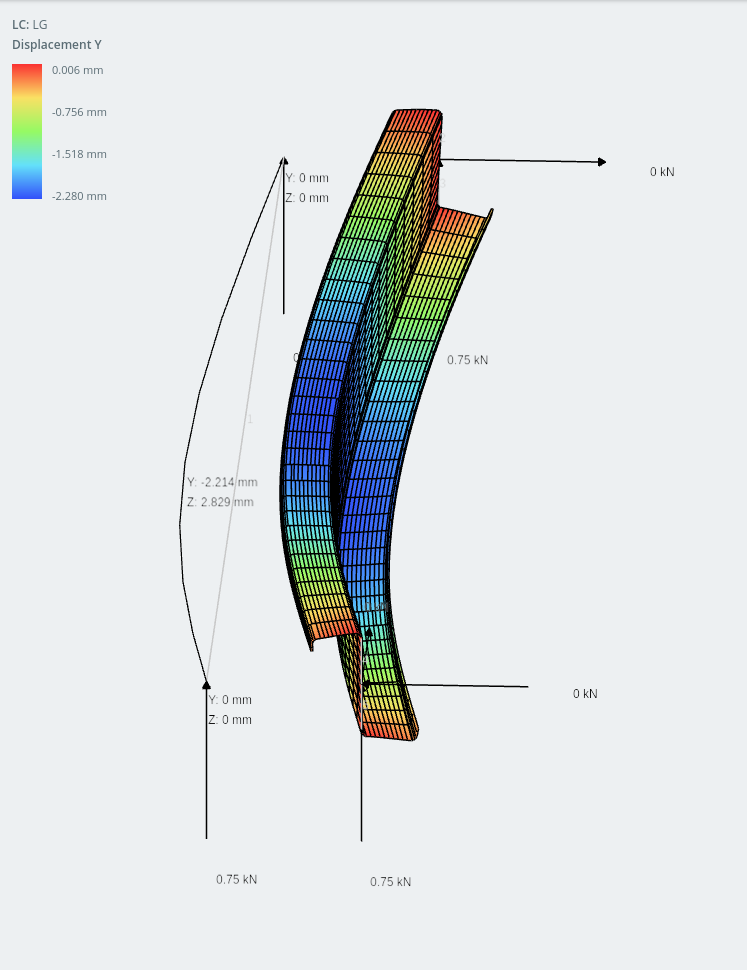
唇形-Z 截面 (显示的垂直位移)

可以设计非对称截面以在某些应用中具有优势. 也许你会在下一个设计中考虑它们?

我希望你觉得这篇文章很有趣, 如果您对不对称截面有任何疑问或反馈, 或者想看更多这样的内容请在下方留言.