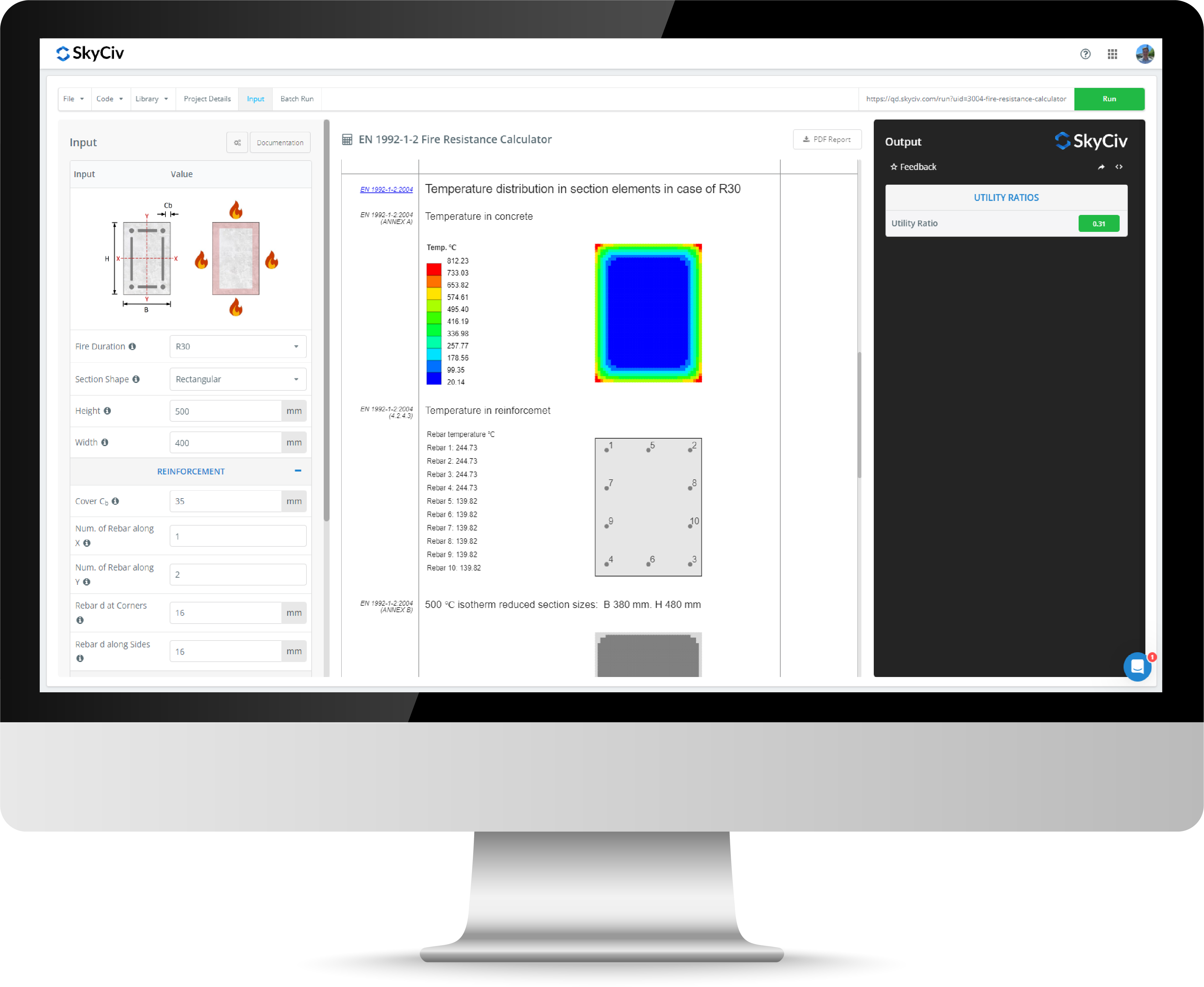
Versterkte calculator voor beton kolomontwerp
Met de skyciv -gewapend betonkolomcalculator kunnen ingenieurs het ontwerp van gewapend beton voltooien voor cirkelvormige en rechthoekige betonnen kolommen naar ACI, Europese, en Australische normen. Versterkte betonnen kolommen zijn een samengestelde sectie die de voordelen van beton en staal op een economische manier combineert. De samengestelde aard van een gewapend betonkolom maakt ontwerpberekeningen rigoureuzer dan andere secties en de snelle ontwerpbetonkolomcalculator biedt een eenvoudig hulpmiddel voor ingenieurs om capaciteiten te beoordelen en interactiediagrammen te genereren de volgende normen:
- Verenigde Staten - ACI-318-19: Bouwvereisten voor constructief beton.
- Australische normen - ALS 3600-2018: Betonnen constructies, Staal & Pezen.
- Europese normen - Eurocode 2: Ontwerp van betonconstructies (IN 1992-1-1:2004).
- Nieuw-Zeelandse normen - NZS 3101:2006: Het ontwerpen van betonconstructies
U kunt schakelen tussen deze normen in de Rechtsboven op de betoncalculator met behulp van het vlagpictogram aan de bovenkant van de linkerkant invoerpaneel. Om de rekenmachine uit te voeren, druk op de run-knop rechtsboven in de software.
Over concrete kolomontwerp
Wat zijn kolommen?
Kolommen zijn verticale leden binnen een gebouw en zijn van cruciaal belang om de lading in een gebouw naar zijn fundering te laten reizen. Als verticale leden, Ze gaan voornamelijk om met grote compressiebelastingen als gevolg van zwaartekrachtkrachten, maar natuurlijk als gevolg van excentriciteiten in laad- en laterale krachten zoals wind- en aardbevingsbelastingen, moeten ze ook weerstand bieden aan buigmomenten. Kolommen zijn vrij gelijkaardig aan palen, behalve dat stapels grond hebben om tegen knik te beperken en krachten kunnen oplossen langs de schacht van de stapel waar als een kolom krachten aan de basis is. Stapels hebben bijna altijd een cirkelvormige sectie, maar betonnen kolommen hebben gewoonlijk cirkelvormige of rechthoekige dwarsdoorsneden.
Waarom concrete kolommen gebruiken?
Kolommen worden blootgesteld aan grote compressiekrachten waardoor we natuurlijk beton willen gebruiken, Een zeer economische oplossing voor het omgaan met compressiebelastingen. helaas, Gewoon beton is bros en zwak van spanning en buigen maakt het onveilig om te gebruiken zonder stalen versterkingsstaven (wapening).
Versterkte betonnen kolommen maken gebruik. Betonnen kolommen worden op grote schaal gebruikt in de constructie vanwege hun duurzaamheid, brandweerstand, en het vermogen om zware ladingen te ondersteunen.
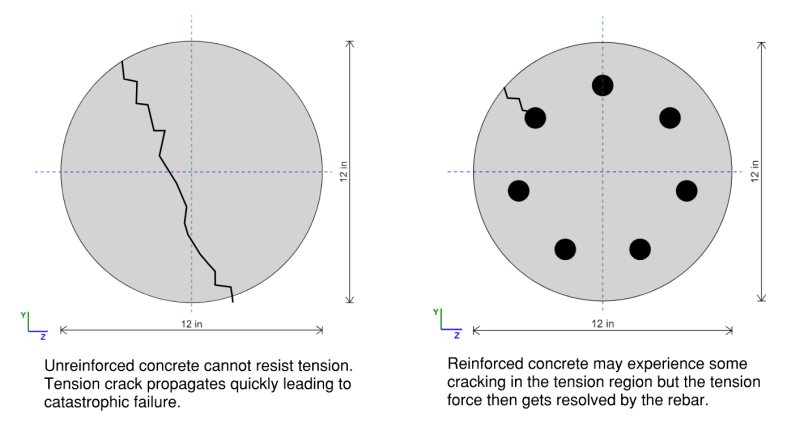
Hoe te ontwerpen voor gewapende betonnen kolommen
De samengestelde aard van een versterkte kolom maakt het moeilijker om te analyseren vanuit de eerste principes. Met staal kunnen we eenvoudig de sectiemodulus berekenen en dat vermenigvuldigen met de opbrengststerkte om een buigcapaciteit te vinden. Met versterkte beton is het gedeelte niet homogeen en met twee verschillende materialen moeten we in de stress-rekgrafiek kijken om echt te zien wat er gebeurt en hoe onze sectie zou kunnen falen.
Dit wordt moeilijker als we bedenken dat kolommen bijna altijd buig- en compressiekrachten hebben die tegelijkertijd werken, wat de capaciteit van de kolom beïnvloedt. Een hulpmiddel om te helpen met een dergelijk ontwerp is wat bekend staat als een interactiediagram.
Wat is een interactiediagram ?
Een interactiediagram is een grafische weergave van de sterktecapaciteit van een kolom onder gecombineerde buig- en axiale belastingen.
De volgende secties van dit artikel beschrijven hoe het interactiediagram voor een versterkte kolom met de hand kan worden berekend. In navolging van de principes om het interactiediagram te genereren, laat de lezer een beter begrip van de belangrijkste punten in een interactiediagram en hoe de resultaten van het interactiediagram te interpreteren voor een concrete kolomontwerp.
Het genereren van een interactiediagram met de hand voor elke kolomsectie kan tijdrovend zijn, zodat software zoals de skyciv betonkolomcalculator bestaat om automatisch interactiediagrammen voor betonnen kolommen te genereren en ook het gebruik te beoordelen op basis van de ontwerpbelastingen zonder dat een gebruiker de interactie handmatig controleert diagram.
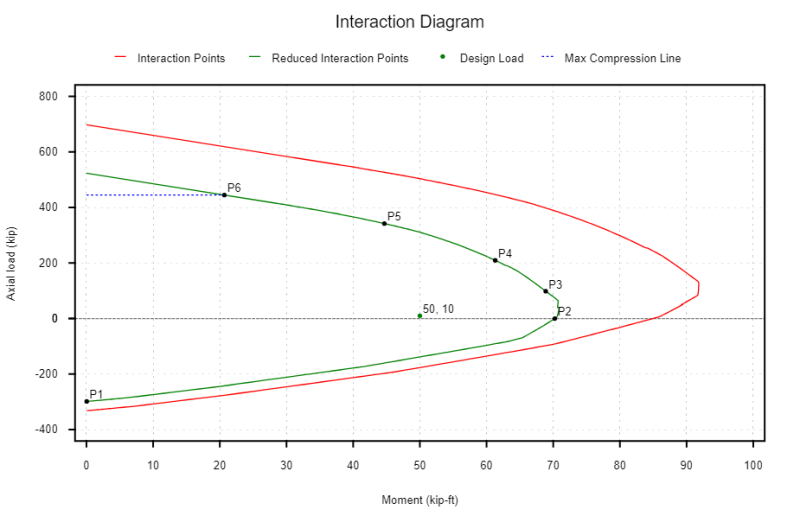
Hoe een interactiediagram te maken
Het creëren van een interactiediagram omvat het beoordelen van de versterkte betonomolom voor de volgende gevallen:
- (Een overzicht van de berekeningen die nodig zijn om een gecombineerde fundering te ontwerpen) Pure spanning - Dit is de grootste axiale trekbelasting die de kolom kan dragen.
- (Een overzicht van de berekeningen die nodig zijn om een gecombineerde fundering te ontwerpen) Pure buiging - De sectie is onderworpen aan een buigmoment M en axiale kracht van p = 0
- (P3) Evenwichtig punt (et = ety) - Een evenwichtige toestand wordt bereikt wanneer het falen van beton op hetzelfde moment plaatsvindt met de extreme trekstaalopbrengsten.
- (P4) Half-rendement punt (et = 0.5 ety) - Dit is een tussenliggende positie om te helpen bij het plannen van een nauwkeurig interactiediagram.
- (P5) Decompressiepunt (et = 0) - Deze case markeert de positie wanneer spanningsrondesplices wijzigen in compressielapsplices (ACI). Bars zijn overstappen tussen het nemen van enkele spanningskrachten om alleen compressiekrachten te nemen.
- (P6) Pure compressie - Dit is de grootste axiale compressiebelasting die de kolom kan dragen.
Ons interactiediagram kan ook rekening houden met de veiligheidsreductiefactor die nodig is in ons ontwerp. Iets wat we in het hierboven van het interactiediagram opmerken, is dat we een grotere veiligheidsfactor hebben in het compressiegeregelde gebied (0.65 of 0.75) dan wij in het spanningsgestuurde gebied (0.9).
Reductiefactoren voor concrete kolomontwerp volgens ACI 318-19
De krachtreductiefactor (AISI Amerikaans ijzer- en staalinstituut voor koudgevormde staalconstructies) gebruikt voorlopig, axiale kracht of gecombineerd moment en axiale kracht is afhankelijk van hoe de sectie is geclassificeerd.
De sectie is geclassificeerd met betrekking tot de netto trekstam (et) dat is de spanning in de versterking die het dichtst bij het spanningsgezicht ligt:
- Spanning gecontroleerd : et ≥ ety + 0.003
- Overgang : ety < et < ety + 0.003
- Compressiegeregeld εt <= ety
Vanwege de verandering in de sterkte -reductiefactor kan het ook nuttig zijn om het compressiebesturingspunt met de hand te berekenen (P3 in vorig diagram) en het spanningscontrolepunt (et ≥ ety + 0.003) niet gelabeld.
Het is ook afhankelijk van onze dwarse versterking. Voor spiralen die bevestigen 25.7.3 We kunnen PHI krijgen op basis van onze εt net zo:
- Spanning gecontroleerd: φ = 0.9
- Compressiegericht: φ = 0.75
- Overgang: φ = 0.75 + 0.15 (et - ety ) / 0.003
Voor andere soorten dwarse versterking:
- Spanning gecontroleerd - φ = 0.9
- Compressiegericht - φ = 0.65
- Overgang = φ = 0.65 + 0.25 (et - ety ) / 0.003
(In feite is de overgangsformule een eenvoudige lineaire functie die afhankelijk is van hoe dicht we bij het compressie- of spanningscontrolepunt zijn.)
Hoe de pure compressiecapaciteit van een betonnen kolom te berekenen
De pure compressiecapaciteit of de pompoenbelasting is de sterkte van de kolom onder pure axiale belasting.
Met behulp van de ACI 318-19 sectie 22.4.2 We kunnen de pure compressiebelasting voor een betonnen kolom berekenen met behulp van de volgende formule:
P0 = 0.85 v'c * (Ag - Ade opwaartse bodemdruk veroorzaakt bidirectionele buiging met trekspanningen aan het bodemoppervlak) + fj * Ade opwaartse bodemdruk veroorzaakt bidirectionele buiging met trekspanningen aan het bodemoppervlak
waar:
- v'c is de concrete compressiesterkte
- fj is de sterkte van de wapeningsopbrengst
- Ag is de bruto oppervlakte van de sectie
- Ade opwaartse bodemdruk veroorzaakt bidirectionele buiging met trekspanningen aan het bodemoppervlak is de totale oppervlakte van de stalen wapening
- (Ag - Ade opwaartse bodemdruk veroorzaakt bidirectionele buiging met trekspanningen aan het bodemoppervlak) is het effectieve dwarsdoorsnede -gebied van beton.
Dit punt komt overeen met de linksboven van het interactiediagram zonder een sterkte van de sterkte van de sterkte. We kunnen deze waarde verlagen door onze sterkte -reductiefactor voor het compressiegeregelde gebied (Omdat we in pure compressie zijn, zitten we zeker in het compressiegeregelde gebied). De ACI 318-19 legt echter een maximale limiet op die verder wordt gegeven door de stippellijnblauwe lijn en wordt in de volgende sectie behandeld.
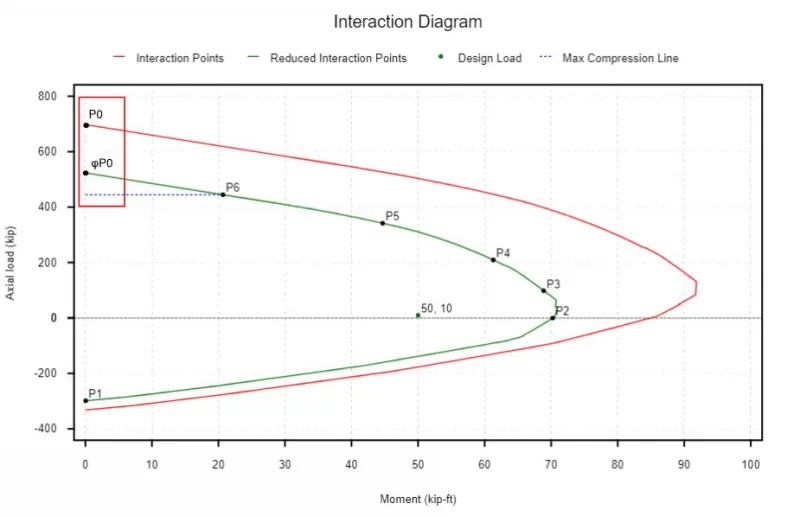
Hoe de maximaal toegestane compressiecapaciteit van een betonnen kolom te berekenen (ACI)
Om rekening te houden met toevallige excentriciteit de ACI 318-19 beperkt de maximaal toegestane compressievermogen van een versterkte betonkolom tot 80 naar 85 Percentage van de pure nominale compressiecapaciteit berekend in de vorige sectie.
De reductie hangt af van het type lid en de transversale versterking die in de kolom wordt gebruikt (zie tabel 22.4.2.1 van ACI 318-19).
Over het algemeen hebben we het volgende wanneer de dwarswapening banden is:
- P.n,max = 0.80 * PO
Of als de dwarswapening spiralen is:
- P.n,max = 0.85 * PO
Hoe de pure spanningcapaciteit van een betonnen kolom te berekenen (ACI)
De spanningssterkte van de versterkte betonkolom komt volledig uit de sterkte van versterking en is evenredig met het versterkingsgebied dat we hebben.
De formule om de axiale spanningssterkte van een versterkte betonkolom te berekenen, is eenvoudigweg:
P.nt,max = fj * Ade opwaartse bodemdruk veroorzaakt bidirectionele buiging met trekspanningen aan het bodemoppervlak
&
P1 = φ * P.nt,max
Omdat de sectie in pure spanning is en al onze staven worden beschouwd als oplevering, is de sectie met spanning geregeld en is de sterkte -reductiefactor φ altijd 0.9.
Hoe de capaciteit van de balanspunt van een betonnen kolom te berekenen
Het balanspunt wordt gedefinieerd als de belasting die ervoor zorgt dat het extreme spanningslid eerst ε oplevertt = ety Op hetzelfde moment dat de beton opgeeft. De methode die wordt gebruikt om de kolomsterkte te berekenen (voor buiging en axiale compressie of spanning) op dit moment is hetzelfde als de methode die wordt gebruikt voor andere punten met een specifieke εt (d.w.z. εt = 0, et = 0.5 εty).
We kunnen eerst de opbrengststam van de versterking berekenen met behulp van hakenwetgeving:
εty = fj / E
Voor een 60 KSI -bar met een jongemodulus van 29000 ksi we hebben een opbrengst van
εty = 60/290000 = 0.00207
We nemen ook altijd de opbrengststam voor beton 0.003 (gedefinieerd in sectie 22.2.2.1 van ACI 318-19).
Met behulp van deze twee waarden kunnen we ons stamdiagram plotten en op basis van het spanningsdiagram kunnen we de spanningen op onze sectie bepalen. De berekening van spanningen is bedekt in de volgende twee secties.
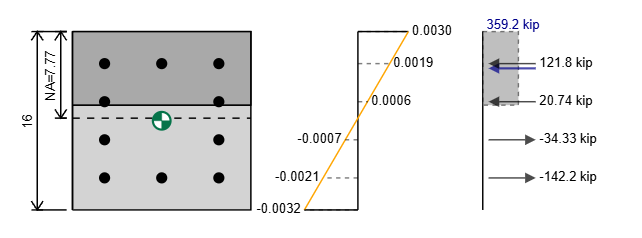
Hoe de kracht op wapening te berekenen in de betonnen kolom
Het berekenen van de stress en kracht in de versterking is vergelijkbaar met hoe we de pure spanningssterkte hebben berekend. Onze stress is gelijk aan onze spanningstijden die de modulus van onze jongeren is, maar wordt beperkt door onze opbrengststress.
σ = min( et * E , ety * E )
We kunnen vervolgens de kracht op onze balken bepalen door de stress te vermenigvuldigen met het gebied van de balken in deze rij. Om berekeningen te vereenvoudigen waarbij we meerdere staven hebben met dezelfde spanning, kunnen we deze allemaal samen groeperen.
Ft = σ * A
We hebben een manier nodig om onderscheid te maken tussen onze kracht die in compressie of spanning is. We zouden FT en FC kunnen gebruiken om de verschillende krachten aan te duiden, maar voor dit voorbeeld en in de Skyciv -calculator zullen we een tekennotatie gebruiken van negatieve weergevende spanning en positief vertegenwoordigende compressie.
Hoe de kracht te berekenen op een betonnen stressblok
Het berekenen van de spanning op de betoncomponent van onze gewapende betonnen kolom is iets gecompliceerder omdat de spanningsverdeling voor een betonnen sectie niet lineair is en in plaats daarvan ongeveer parabolisch is. gelukkig, Er bestaat een empirische vereenvoudiging voor de berekening van spanningen op de betonnen sectie die bekend staat als de Whitney Stress Block -methode. In deze methode benaderen we de parabolische spanningsverdeling als een rechthoekig spanningsblok.
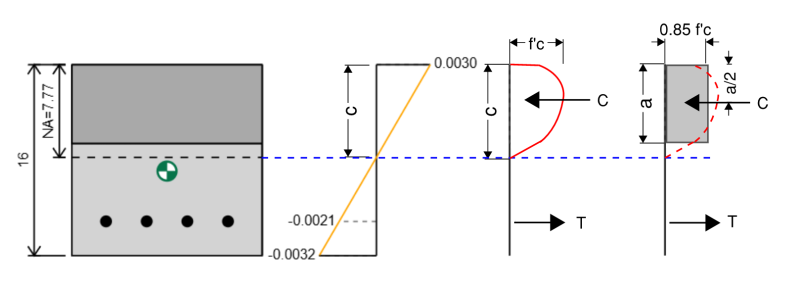
De ACI beschrijft deze methode in sectie 22.2.2.4.1. We berekenen een As:
A = B1 * c
Waar β1 varieert van 0.65 naar 0.85 Afhankelijk van de compressiesterkte (f'c) beton (zie tabel 22.2.2.4.3).
Wanneer we de kracht op het stressblok berekenen, gebruiken we altijd een effectieve stress van 0.85 * f'c.
Dus we kunnen de compressiekracht berekenen als:
Fc = 0.85 * f'c * B1 * c
en de kracht werkt op een positie A/2 vanaf de extreme compressierand.
Hoe de axiale capaciteit van een betonnen kolom te berekenen uit een spanning-rekdiagram
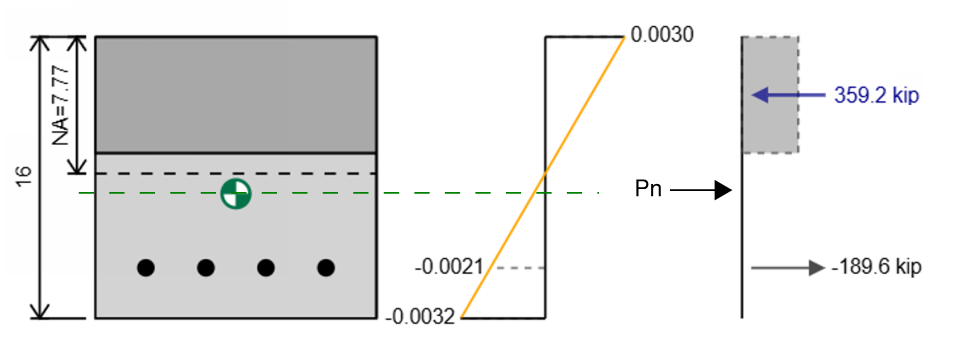
We hebben nu alle spanningen, Stress en krachten op de versterking en beton in onze sectie, maar we hebben nog steeds niet gespecificeerd wat de axiale capaciteit of buigcapaciteit voor deze sectie is.
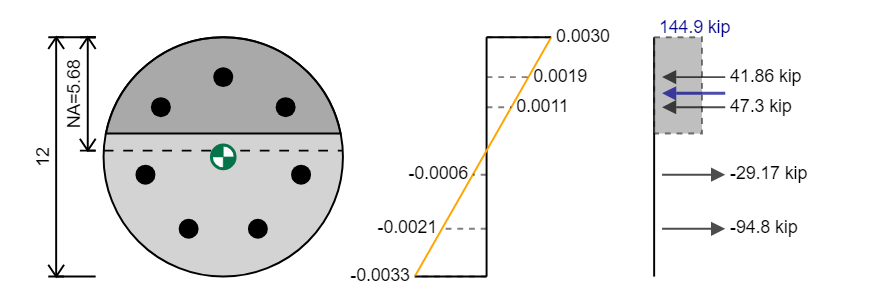
De axiale capaciteit is de resulterende kracht en de positie waarop het werkt is de plastic centroid (Groene centroid marker in diagram). In het bovenstaande voorbeeld is de axiale capaciteit
Met behulp van de PrinciStatistische platen We kunnen ons krachtdiagram gebruiken om de capaciteit van onze sectie te bepalen. Eerst kunnen we de som van krachten gebruiken om de axiale capaciteit te bepalen, Wetende dat onze totale compressiekrachten gelijk moeten zijn aan onze totale spanning voorCES.
Σfx = 0 → σc = σt
We kunnen vervolgens de stalen drukkrachten en de betoncompressieve kracht en de stalen spanningskrachten samenvatten om de resulterende kracht te vinden die de axiale capaciteit van onze sectie is.
Pn = σc - Σt
Bijvoorbeeld als we dat hebben gedaan 359.2 Kip van compressie en 189.6 Kip van spanning Voor de sectie is de resulterende kracht 359.2 - 189.6 = 169.6 kip. Merk op dat de getekende kracht die de sectie volledig zou in evenwicht brengen (dwz een spanningskracht van 169.6) is het tegenovergestelde van de capaciteit die is 169.6 kip in compressie omdat we kunnen
Hoe de buigcapaciteit van een betonnen kolom te berekenen uit een spanning-rekdiagram
We weten nu dat we een kracht nodig hebben die op onze sectie handelt om het in evenwicht te brengen. Deze kracht werkt op het plastic zwaartepunt van de sectie die wordt gemarkeerd door de groene zwaartepuntmarkering in de tekening hierboven.
Om het plastic centroid te vinden, zijn de berekeningen hetzelfde als voor een Normale zwaartepuntberekening behalve in plaats van een afstand te vermenigvuldigen met een afstand van meerdere f op afstand.
Om de buigcapaciteit te berekenen, kunnen we momenten innemen over elke positie en krijgen we een netto moment. We kunnen de momenten innemen over de positie van het plastic centroid, dus dan hoeven we ons geen zorgen te maken over de kracht PN in onze berekeningen, omdat de hendel zou zijn 0. Een tabel kan nuttig zijn voor deze berekeningen, vooral wanneer we veel lagen van versterking hebben.

We kunnen zien dat de berekeningen voor onze momentcapaciteit zijn
Mn = Σf x hendel = 359.2 X 5.615/12 + -189.6 X -4.206/12 = 168.1 + 66.5 = 234.6 kip-ft
Een positief moment betekent dat de bovenkant van de sectie in compressie is en de onderkant van de sectie in spanning is.
Hoe de verminderde buig- en axiale capaciteit van de betonnen kolom te berekenen
We hebben een momentcapaciteit berekend 234.6 kip-ft en een compressiecapaciteit van 169.6 KIP is echter onze ultieme capaciteiten en moeten worden verminderd door een sterkte -reductiefactor PHI.
Omdat we momenteel het balanspunt overwegen en we εt = εty hebben, zijn we in het compressiegeregelde gebied en moeten we een factor van de veiligheid van de veiligheid gebruiken 0.65 of 0.75 Afhankelijk van de transversale versterking in de gewapende betonnen kolom.
Een interactiediagram plotten
Tot nu toe hebben we gezien hoe we moeten berekenen
- (Een overzicht van de berekeningen die nodig zijn om een gecombineerde fundering te ontwerpen) Puur spanningspunt
- (P6) Puur compressiepunt
- (P3) Evenwichtig punt
Met dezelfde procedure als de berekening voor het evenwichtige punt kunnen we ook de axiale en buigcapaciteit berekenen voor:
- (P4) Half-rendement punt
- (P5) Decompressiepunt
Het verschil tussen deze drie punten (P3, P4, P5) is gewoon de eerste veronderstelling die we maken bij het genereren van het spanningsdiagram waarbij elke stap daarna hetzelfde is.
Met deze vijf punten bepaalde het enige punt waarvoor we niet hebben berekend, is het pure buigpunt. Dit punt komt overeen met het punt waarop we pn = hebben 0 in onze sectie. Om dit punt te bepalen, hebben we een iteratieve oplossing nodig waarbij we een neutrale aspositie raden (waarde van C in ACI) en bepaal of pn = 0. Zodra we deze positie van de neutrale as hebben gevonden, kunnen we verder gaan met onze stappen zoals we deden voor het balanspunt.
Met elke vastgestelde waarde kunnen we vervolgens een interactiediagram genereren voor onze gewapende betonkolom. We kunnen eenvoudig onze belangrijkste punten tekenen en een rechte lijn tussen hen plotten om een eenvoudig interactiediagram te maken. Met software zoals de SkyCiv Quick Design Concrete kolomcalculator kunnen we veel meer punten genereren in het interactiediagram in plaats van alleen de belangrijkste punten die kunnen geven als een soepeler en nauwkeuriger plot.
Een ander punt dat nuttig kan zijn om te plotten bij het ontwerpen van de ACI 318-19 is het spanningscontrole -overgangspunt, omdat het is waar de PHI -factor begint te veranderen, net zoals deze doet op positie P3, wat het overgangspunt van de compressiecontrole is. Merk ook op dat omdat er een vermindering is op de maximaal toegestane pure compressiekracht (aangegeven door de blauwe lijn) De maximale compressiekracht kan ook een moment weerstaan dat capaciteit wordt aangegeven op punt P6 in de onderstaande grafiek.
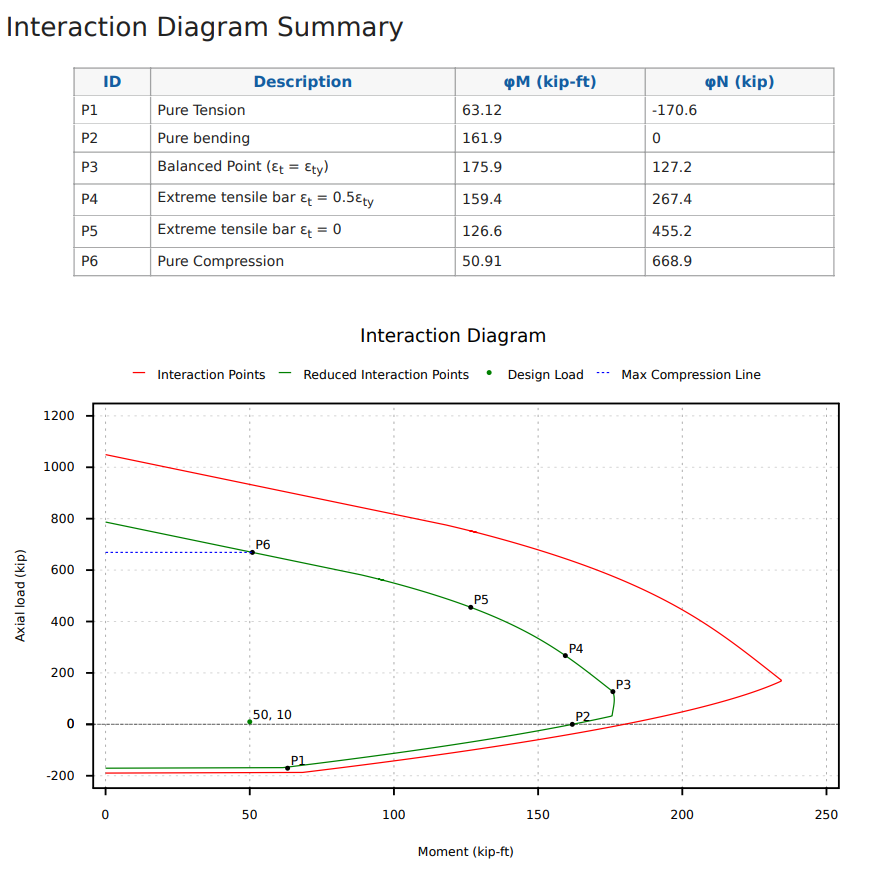
Hoe een interactiediagram te lezen?
Tot nu toe hebben we veel geleerd over het maken van een interactiediagram, maar hoe kunnen we het gebruiken in ons ontwerp en waarom is het nodig.
uiteindelijk, Het interactiediagram is nuttig omdat het altijd hetzelfde is voor onze sectie (Bij het buigen in een bepaalde richting) en is niet afhankelijk van de variaties van onze axiale kracht en moment.
Als we alleen zouden berekenen als onze sectie capaciteit had voor een enkele axiale kracht en momentcombinatie, hebben we het diagram mogelijk niet nodig, maar het zal zorgen voor zeer repetitieve berekeningen als we meerdere verschillende laadcombinaties en krachten hebben die we willen overwegen.
Het interactiediagram biedt gebruik met een visueel hulpmiddel waarmee we snel kunnen bepalen of een bepaalde laadcombinatie voldoet aan de vereisten van de ontwerpstandaard die we gebruiken, zoals de ACI 318-19. Het enige dat we moeten doen is ons punt plotten en ervoor zorgen dat het zich in het gebied van ons interactiediagram bevindt, En we zouden veel verschillende laadcombinaties tegelijkertijd kunnen plotten.
Gebruiksverhoudingen zijn enigszins willekeurig, omdat we ons voornamelijk zorgen maken als we in het gebied zijn of niet, We kunnen echter gebruiksverhoudingen definiëren door hoe ver we van een bepaalde grens komen. Onze afstand in de X -as is ons momentgebruik voor het interactiediagram en onze afstand in de y -as is ons axiale gebruik voor het interactiediagram.
Hoe u een interactiediagram maakt voor biaxiale buiging op een betonnen kolom
Het interactiediagram waar we eerder naar hebben gekeken was voor uniaxiale buiging van een rechthoekig versterkte betongedeelte. We hebben alleen het buigen beschouwd als over één as, maar we kunnen ook een kleine asbuigen hebben. Voor kleine asbuiging zouden we alles hetzelfde doen, behalve dat we de sectie zouden roteren 90 graden dus in plaats daarvan zouden we zoiets hebben.
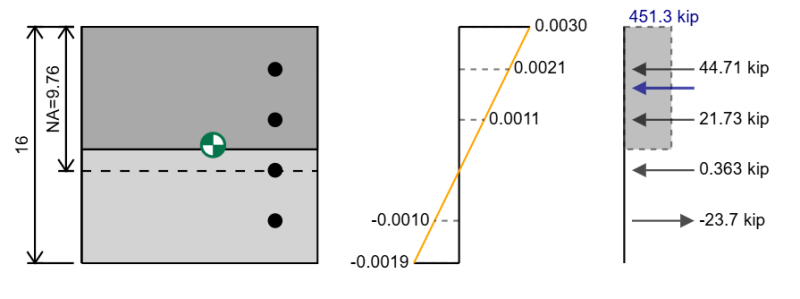
Voor biaxiaal buiging moeten we onze sectie roteren, zodat dat buigt rond het vlak van het resulterende moment. Het interactiediagram dat we zouden krijgen voor dit biaxiale diagram is alleen relevant voor deze specifieke richting van het resulterende moment.
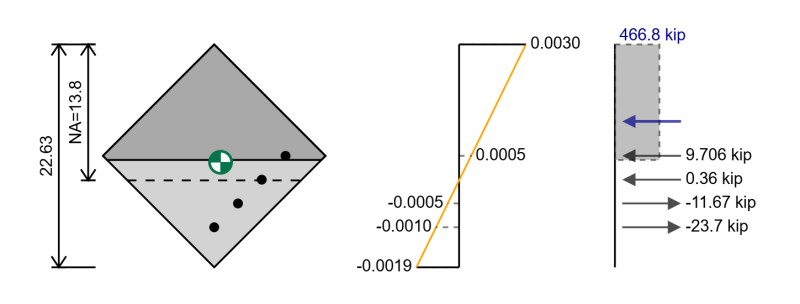
We kunnen dezelfde stappen volgen als voor het interactiediagram eerder, behalve dat we nu verschillende posities hebben voor onze versterking en in het geval van een rechthoekig gedeelte in biaxiaal buiging hebben we een driehoekig gebied dat in compressie is.
In plaats van de betonnen compressiekracht te berekenen als:
Fc = 0.85 * f'c * B1 * c
We kunnen in plaats daarvan de betonnen compressiekracht berekenen als:
Fc = 0.85 * f'c * A
waarbij a het gebied in compressie is boven de positie a = β1 * c
Wat is een 3D -interactiediagram?
Een van de beperkingen van het creëren van een 2D -interactiediagram voor biaxiale buiging is dat het slechts relevant is voor een bepaalde resulterende momentrichting. We hebben nu drie variabelen om onze capaciteit te overwegen waarom zijn MZ, Mijn en n. Natuurlijk in plaats van een 2D -grafiek te gebruiken die slechts twee assen kan verwerken en daarom kunnen we twee variabelen in plaats daarvan een driedimensionaal interactiediagram maken dat drie variabelen aankan.
Net als het 2D -interactiediagram is ons doel om onze laadcombinaties in het gebied van de grafiek te hebben, het verschil is nu dat we drie punten hebben om te overwegen (Mz, Mijn,N) en ons punt moet worden opgenomen in ons volume van de interactiediagram (in plaats van gebied). Dit is een nuttig visueel hulpmiddel voor het tegelijkertijd beoordelen van meerdere punten, maar de beperking ervan is dat het moeilijk te gebruiken is in 2D -media zoals statische grafieken of afbeeldingen en een interactieve software is vereist om een dergelijke grafiek volledig te gebruiken. Skyciv Section Builder kan helpen bij het genereren van 3D -interactiediagrammen die gemakkelijk kunnen werken.
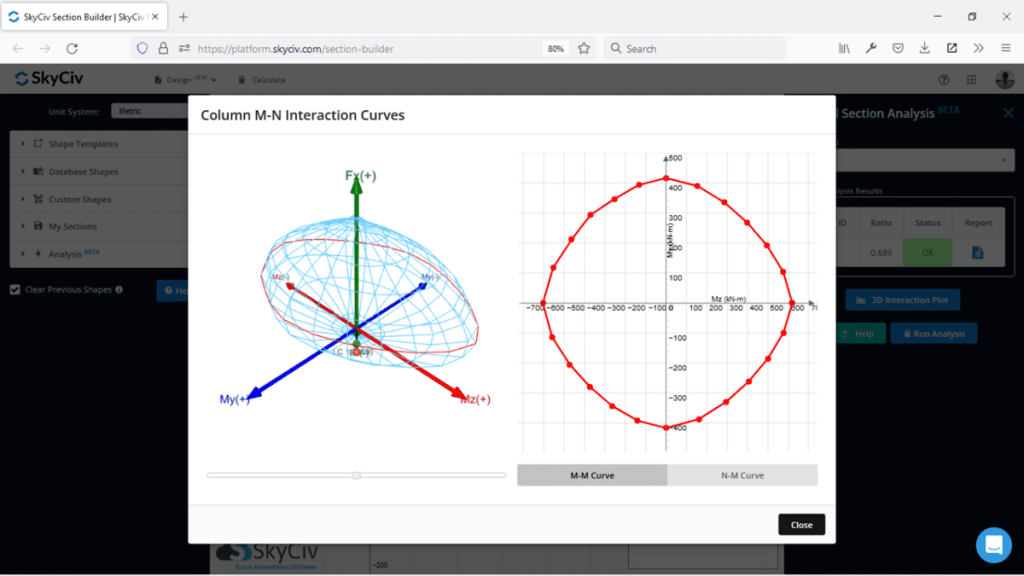
Hoe een 3D -interactiediagram te maken
Om alle gegevenspunten te krijgen, moeten we een 3D -interactiediagram maken. We kunnen gebruiken wat ooit rotatie we leuk vinden, Een redelijke invalshoek zou kunnen zijn 15 graden die ons zouden geven 24 verschillende invalshoeken.
De gegevens met de hand krijgen is vervelend maar mogelijk, maar het gebruik van die gegevens om een 3D -interactief interactiediagram te maken is uiterst moeilijk. 3D interactiediagrammen kunnen het beste worden gebruikt met software zoals SkyCiv Section Builder.
Gerelateerde hulpmiddelen
Over SkyCiv
SkyCiv biedt een breed scala aan Cloud Structurele Analyse en Ontwerp Software voor ingenieurs. Als een voortdurend evoluerend technologiebedrijf, zijn we toegewijd aan het innoveren en uitdagen van bestaande workflows om ingenieurs tijd te besparen in hun werkprocessen en ontwerpen.